Guía UNAM Matemáticas: Área 2 Cs Biológicas Químicas y Salud P.1

¡Nos vemos de nuevo aspirante! En este tutorial estaremos resolviendo los reactivos de matemáticas área 2, del 46 al 57, que se encuentran en la guía de Ciencias Biológicas, Químicas y de la Salud de cara al examen de ingreso UNAM.

¿Cómo estudiar la guía UNAM? Te aconsejo desarrollarlos por tu cuenta antes de checar la solución. Es importante que estudies y comprendas cada uno de los temas del examen, tu calificación es proporcional al esfuerzo que hayas dedicado al prepararte.

A continuación, tienes un resumen de los puntos más importantes sobre el examen de ingreso UNAM.

• Desarrollo: UNAM
• Área 2: Ciencias Biológicas, Químicas y de la Salud
• Materia: Matemáticas
• Reactivos: 120
• Tipo: Opción múltiple
• Duración: 3 horas
• Modalidades: Presencial

Las carreras con mayor porcentaje de rechazo de la UNAM pertenecen al área 2. Asegúrate de estudiar muy bien los temas de cada asignatura.

Estructura del examen

El examen a la Universidad Nacional Autónoma de México se compone de 120 reactivos, de los cuales 24 pertenecen a matemáticas para el área 2 Ciencias Químicas, Biológicas y de la Salud.

En la siguiente tabla, encontrarás la estructura del examen a la UNAM para el área 2, con el total de reactivos por asignatura que deberás resolver.

Temas	Área 2
Español	18
Matemáticas	24
Física	12
Química	13
Biología	13
Historia universal	10
Historia de México	10
Literatura	10
Geografía	10
Filosofía	NA
Total	120

Médico Cirujano del área 2 en la UNAM, es una de las carreras más demandadas y la segunda con más aciertos mínimos.

De las 130 carreras que oferta la Universidad Nacional Autónoma de México, 31 de ellas pertenecen al área 2 de Ciencias Químicas, Biológicas y de la Salud, de las cuales, 9 poseen modalidad de ingreso indirecto.

¿Cómo estudiar matemáticas?

Aunque la carrera que deseas ingresar pertenece al área 2, la asignatura de matemáticas es determinante tanto para la prueba de ingreso como para el resto de la carrera. Gracias a las matemáticas, podemos representar al mundo que nos rodea mediante modelos fáciles de estudiar, con la posibilidad de extender nuestra percepción de la naturaleza.

La capacidad de análisis y abstracción que nos brindan las matemáticas son aplicables a cualquier situación y transversales a todas las ciencias exactas y humanas. Por esta razón, te dejo algunos consejos que debes tener en cuenta a la hora de estudiar matemáticas.

Guía matemáticas UNAM área 2 resuelta

Comenzamos con la solución paso a paso con los reactivos de matemáticas, para la guía UNAM del área 2 de Ciencias Biológicas, Químicas y de la Salud.

Reactivo 46

Si 127 es el dividendo y 11 es el divisor en la ecuación, ¿cuánto valen el cociente c y el residuo r?

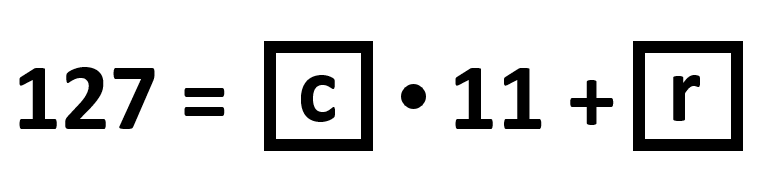
1. c=11 y r=0
2. c=12 y r=-5
3. c=10 y r=17
4. c=11 y r=6

Solución:

Para resolver el problema, vamos a calcular el cociente entre 127 y 11, hasta que los valores del residuo y del cociente correspondan con alguno de los incisos.

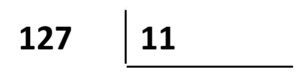
Bajamos al 12 y multiplicamos el divisor por 1.

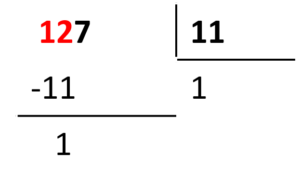
Bajamos al 7 y multiplicamos el divisor por 1 nuevamente.

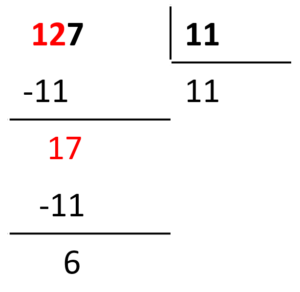
El cociente es igual a 11 y el residuo es 6.

127=\left(11\right)\left(11\right)+6=127

c=11, r=6

La respuesta correcta es el inciso D.

Reactivo 47

Factoriza la siguiente expresión.

{n}^{6}-3{n}^{3}-18

1. \left({n}^{3}+3\right)\left({n}^{3}-6\right)
2. \left({n}^{3}-3\right)\left({n}^{3}+6\right)
3. \left({n}^{3}-3\right)\left({n}^{3}-6\right)
4. \left({n}^{3}+3\right)\left({n}^{3}+6\right)

Solución:

Iniciamos aplicando el siguiente cambio de variable:

q={n}^{3}

De tal forma que:

{n}^{6}-3{n}^{3}-18={\left({n}^{3}\right)}^{2}-3{n}^{3}-18

{q}^{2}-3q-18

Para factorizar a este polinomio, buscamos dos números que sumados sean -3 y que multiplicados -18. Estos valores son: -6 y 3.

-6+3=-3

\left(-6\right)\left(3\right)=-18

Factorizamos:

  {q}^{2}-3q-18=\left(q-6\right)\left(q+3\right)

Ahora, devolvemos el cambio de variable:

\left(q-6\right)\left(q+3\right)\to \left({n}^{3}-6\right)\left({n}^{3}+3\right)

Finalmente:

{n}^{6}-3{n}^{3}-18=\left({n}^{3}-6\right)\left({n}^{3}+3\right)

Concluimos que la respuesta correcta es el inciso A.

Reactivo 48

Selecciona la expresión que corresponde a una ecuación:

1. \mathrm{sen}\left(x\right)=\frac{1}{2}
2. \mathrm{sen}\left(x\right)=\frac{1}{2}x
3. {\mathrm{sen}}^{2}\left(x\right)+{\mathrm{cos}}^{2}\left(x\right)=1
4. {\mathrm{sec}}^{2}\left(x\right)-{\mathrm{tan}}^{2}\left(x\right)=1

Solución:

Para llegar a una conclusión, debemos saber diferenciar entre una igualdad y una identidad. Las igualdades se cumplen solo para ciertos valores de la(s) variable(s), mientras que una identidad se cumple para todos los posibles valores de la(s) variable(s).

Un ejemplo claro de identidad se encuentra en los incisos C y D. Corresponden a la identidad Pitagórica en términos de seno y coseno y secante y tangente, respectivamente. Sin importar el valor de x que selecciones, el resultado será siempre 1.

Por otro lado, los incisos A y B se cumplen solo para ciertos valores de x , ambos (en efecto) son ecuaciones. La diferencia está en la naturaleza de ambas ecuaciones.

La primera se resuelve aplicando seno inverso de ambos lados, mientras que la otra es una ecuación trascendente; no posee solución analítica.

Basados en todo nuestro análisis, escogemos la expresión del inciso A como respuesta correcta. Hacemos hincapié en que, tanto A como B son ecuaciones, solo que B es trascendente y no hay manera de encontrar su valor realizando operaciones.

Reactivo 49

Las soluciones de la ecuación 4{x}^{2}+16x+15=0 son:

1. {x}_{1}=-\frac{3}{2}, {x}_{2}=-\frac{5}{2}
2. {x}_{1}=3, {x}_{2}=-\frac{5}{4}
3. {x}_{1}=\frac{3}{2}, {x}_{2}=\frac{5}{2}
4. {x}_{1}=-\frac{3}{4}, {x}_{2}=5

Solución:

Debido a que este trinomio tiene el coeficiente a distinto a 1, no podemos factorizar buscando dos números que sumados y multiplicados sean b y c respectivamente. Tampoco podemos extraer ningún factor común. Emplearemos la fórmula de segundo grado:

x=\frac{-b\pm \sqrt{{b}^{2}-4ac}}{2a}

Sustituimos los valores de los parámetros.

x=\frac{-16\pm \sqrt{{\left(16\right)}^{2}-4\left(4\right)\left(15\right)}}{2\left(4\right)}=\frac{-16\pm \sqrt{256-240}}{8}=\frac{-16\pm \sqrt{16}}{8}=\frac{-16\pm 4}{8}

{x}_{1}=\frac{-16+4}{8}=-\frac{3}{2}

{x}_{2}=\frac{-16-4}{8}=-\frac{20}{8}=-\frac{5}{2}

Las raíces del polinomio son: x=-\frac{3}{2}, x=-\frac{5}{2} .

La respuesta correcta es el inciso A.

Reactivo 50

Selecciona la desigualdad que tiene por solución al siguiente conjunto.

\left(-\infty ,\frac{2}{6}\right]

1. 3x-1\ge 0
2. 2x-6\ge 0
3. -3x+1\ge 0
4. -2x+6\ge 0

Solución:

Primero, vamos a simplificar al extremo superior del intervalo.

\left(-\infty ,\frac{2}{6}\right]=\left(-\infty ,\frac{1}{3}\right]

Ahora, vamos a ir resolviendo las inecuaciones de los incisos hasta encontrar una cuyo conjunto solución sea el mostrado por el enunciado.

Primera inecuación.

3x-1\ge 0\to 3x\ge 1\to x\ge \frac{1}{3}

El conjunto solución es: \left[\frac{1}{3}, \infty \right) . Esta inecuación no es la correcta.

Segunda inecuación.

2x-6\ge 0\to 2x\ge 6\to x\ge 3

Descartamos también esta inecuación.

Tercera inecuación.

-3x+1\ge 0\to -3x\ge -1

Dividimos por un número negativo, cambia el sentido de la desigualdad.

x\le \frac{1}{3}

El conjunto solución es:

\left(-\infty ,\frac{1}{3}\right]

Concluimos entonces que la respuesta correcta es el inciso C.

Reactivo 51

A partir del siguiente sistema de ecuaciones obtén el valor de x.

\begin{array}{c}5x-4y=19\\ 7x+3y=18\end{array}

1. x=-3
2. x=-1
3. x=1
4. x=3

Solución:

Para calcular el valor de x , podemos emplear cualquier método de solución de sistemas de ecuaciones lineales. En este caso son convenientes los métodos por igualación y el método por determinantes. Vamos a utilizar el primero, despejamos a y de ambas ecuaciones.

Primera ecuación.

5x-4y=19\to -4y=19-5x\to y=\frac{5x-19}{4}

Segunda ecuación.

7x+3y=18\to 3y=18-7x\to y=\frac{18-7x}{3}

Ahora, igualamos las ecuaciones.

\frac{5x-19}{4}=\frac{18-7x}{3}

Simplificamos y despejamos a x .

3\left(5x-19\right)=4\left(18-7x\right)\to 15x-57=72-28x

15x+28x=72+57

43x=129

\therefore x=\frac{129}{43}=3

El valor de x que satisface al sistema de ecuaciones es de ecuaciones es 3.

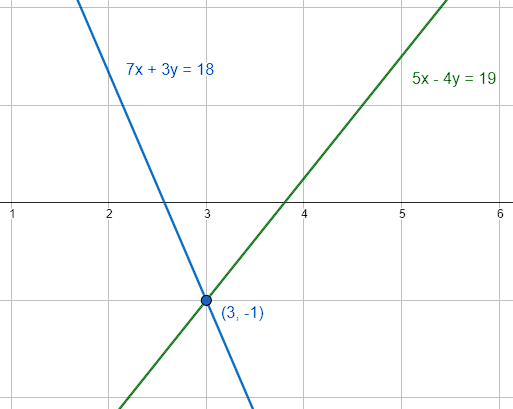
La respuesta correcta es el inciso D.

Reactivo 52

Determina el rango de la función:

f\left(x\right)=5-3{\left(x-2\right)}^{2}

1. y\in R, y\ge 5
2. x\in R, y\in R
3. x\in R, x\ge 5
4. y\in R, y\le 5

Solución:

Para responder esta pregunta, tenemos dos opciones:

• Calcular la inversa de la función y luego calcular el rango.
• Analizar el tipo de función y determinar el rango a partir de esto.

Vamos a resolver el problema empleando el primer camino. Descartamos a los incisos B y C porque en ellos se indica a la variable x , el rango se calcula respecto a la variable y .

Cálculo de la inversa.

Despejamos a x .

y=5-3{\left(x-2\right)}^{2}

3{\left(x-2\right)}^{2}=5-y\to {\left(x-2\right)}^{2}=\frac{5-y}{3}

\therefore x={f}^{-1}\left(x\right)=2\pm \sqrt{\frac{5-y}{3}}

Ahora, el rango será el conjunto de valores para los cuales, la inversa se encuentre definida. La función anterior solo tiene una única restricción y es la del radical.

\frac{5-y}{3}\ge 0\to 5-y\ge 0\to -y\ge -5

\therefore y\le 5

El rango de la función es:

y\in R, y\le 5

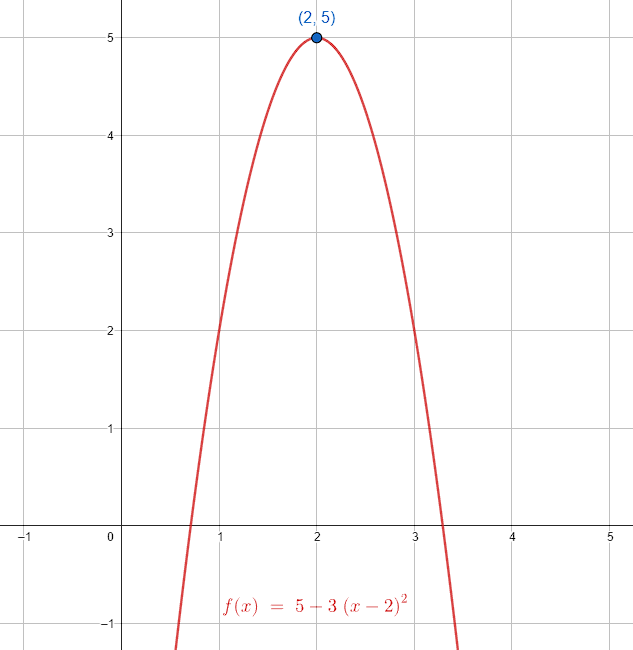
La respuesta correcta es el inciso D. El otro método, se basa en identificar el tipo de función. En este caso, la función es una parábola que abre hacia abajo porque la variable x está negativa.

y=5-3{\left(x-2\right)}^{2}\to -\frac{1}{3}\left(y-5\right)={\left(x-2\right)}^{2}

El signo del coeficiente -\frac{1}{3} nos indica que la parábola abre hacia abajo y las coordenadas del vértice \left(h, k\right)=\left(2, 5\right) , nos indican que la parábola tiene valores en y desde 5 hasta -\infty  .

Reactivo 53

¿Cuál es el seno del ángulo A en el triángulo rectángulo siguiente?

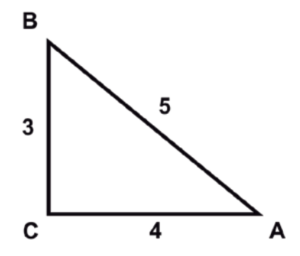
1. \frac{3}{5}
2. \frac{4}{5}
3. \frac{5}{3}
4. \frac{5}{4}

Solución:

El seno del ángulo A es igual al cociente entre el cateto opuesto al ángulo sobre la hipotenusa.

\mathrm{sin}A=\frac{CO}{H}

Respecto al ángulo A , el cateto opuesto es el lado BC=3 . La hipotenusa del triángulo es AB=5 .

\mathrm{sin}A=\frac{3}{5}

La respuesta correcta es el inciso A.

Reactivo 54

Selecciona la función que tiene un desplazamiento de fase de \pi  unidades a la derecha.

1. f\left(x\right)=\mathrm{sin}\left(\pi x\right)
2. f\left(x\right)=\mathrm{sin}\left(x+\pi \right)
3. f\left(x\right)=\mathrm{sin}\left(x-\pi \right)
4. f\left(x\right)=\pi \mathrm{sin}\left(x\right)

Solución:

Cuando en el argumento de una función trigonométrica se suma una determinada cantidad angular, la gráfica de la función se desplaza hacia la izquierda. Por otra parte, si se resta dicha cantidad, el desplazamiento ocurre hacia la derecha.

Teniendo en cuenta esta sencilla regla, concluimos que la respuesta correcta es el inciso C.

Reactivo 55

¿Cuál es el dominio de la siguiente función?

f\left(x\right)=\mathrm{log}\left(x-1\right)

1. x\le 1
2. x<1
3. x>1
4. x\ge 1

Solución:

Para calcular el dominio de una función, debemos identificar el tipo de funciones que la componen y de esa forma, identificar todas sus restricciones. La función del enunciado es logarítmica de base 10, cuya única restricción es que el argumento sea mayor que cero.

x-1>0\to x>1

\mathrm{D}\mathrm{o}\mathrm{m}\left(f\right)=x\in \left(1,\infty \right)

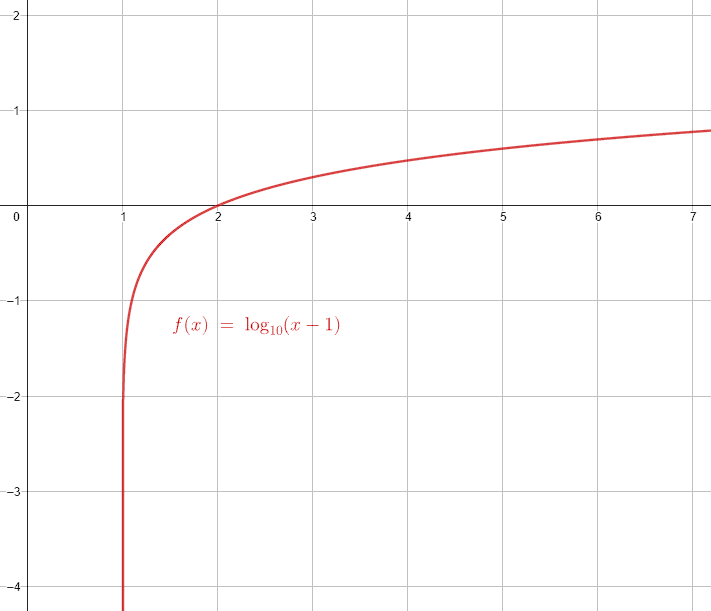
Indicamos como respuesta correcta al inciso C.

Reactivo 56

El punto medio del segmento que une a los puntos A\left(2m,  m+1\right) y B\left(2m,  m–1\right) es:

1. \left(0, 2\right)
2. \left(m, 2m\right)
3. \left(2m, m\right)
4. \left(4m, 2m\right)

Solución:

Para calcular el punto medio de un segmento cuyos extremos son A y B , empleamos la siguiente ecuación:

M=\left(\frac{{A}_{x}+{B}_{x}}{2},\frac{{A}_{y}+{B}_{y}}{2}\right)

Sustituimos en la ecuación las coordenadas de los puntos.

M=\left(\frac{2m+2m}{2},\frac{m+1+m–1}{2}\right)=\left(\frac{4m}{2},\frac{2m}{2}\right)=\left(2m, m\right)

El punto medio del segmento cuyos extremos son A y B es:

M=\left(2m, m\right)

Indicamos como respuesta correcta al inciso C.

Reactivo 57

La pendiente de la recta 3x+6y-1=0 es:

1. -3
2. -\frac{1}{2}
3. \frac{1}{2}
4. 3

Solución:

Para obtener la pendiente de la recta, realizamos el siguiente cociente:

m=-\frac{a}{b}

Donde a y b son los coeficientes de x y y respectivamente. Sustituimos:

m=-\frac{3}{6}=-\frac{1}{2}

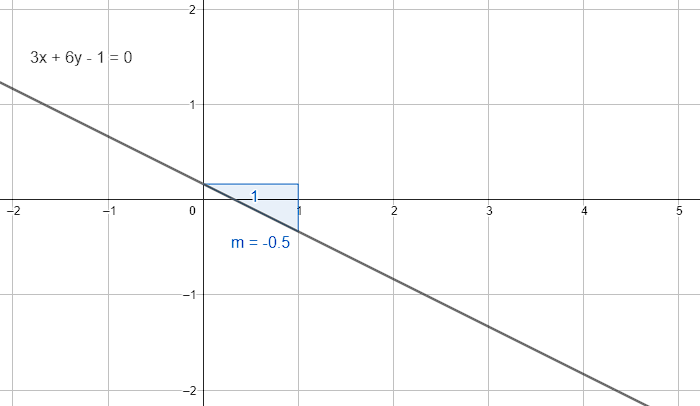
La respuesta correcta es el inciso B.

Temario matemáticas área 2

La lista contiene el temario de matemáticas para el área 2 de la UNAM. Es extenso, pero si planificas tus sesiones de estudio podrás cubrir todo el contenido. Puedes acceder a mayor información sobre el examen y la convocatoria UNAM haciendo clic en este enlace.