Examen Simulador IPN de Cálculo integral: 40 reactivos resueltos

De acuerdo con las opiniones de quienes han presentado el examen, la asignatura de cálculo integral y diferencial representa el mayor desafío dentro de la sección de matemáticas, e incluso, se considera la más compleja de todo el examen de admisión al IPN.

El objetivo principal de este examen simulacro de cálculo integral es permitirte evaluar tu dominio de los conocimientos en la materia. Así, podrás identificar y dedicar tiempo al estudio de los temas que te resulten más difíciles.

¿Qué viene en el examen del IPN?

La estructura del examen del IPN varía según el área a la que pertenece tu carrera, aunque muchos creen que al ser un politécnico su oferta académica es exclusiva de áreas de ingeniería, su oferta académica abarca más de 50 licenciaturas de distintas áreas del conocimiento.

La siguiente tabla muestra la estructura de reactivos para cada área:

Materia	IyCFM	CMB	CSyA
Matemáticas	37	33	35
Competencia escrita	20	20	25
Competencia lectora	20	20	20
Reading comprehension	10	10	10
Historia	10	10	20
Biología	9	17	10
Química	17	17	10
Física	17	13	10

Temario de Cálculo integral

Como te comentamos al inicio, el cálculo integral, que se incluye dentro del apartado de matemáticas, es uno de los más complejos del examen, sobre todo para aquellos que no cuentan con el conocimiento básico en matemáticas.

• Integral indefinida
  • Definición de la antiderivada
  • Constante de integración
  • Fórmulas básicas de integración
• Derivada de funciones algebraicas y trascendentes
  • Por sustitución
  • Integración por partes
  • Sustitución trigonométrica
  • Fracciones parciales
• Integral definida
  • Teorema Fundamental del Cálculo
  • Área bajo la curva
  • Longitud de arco

Toma en cuenta que esta materia viene en el examen de admisión a todas las carreras.

Sin más preámbulo, comienza la solución de los primeros 10 reactivos de cálculo integral para el IPN.

Reactivo 1

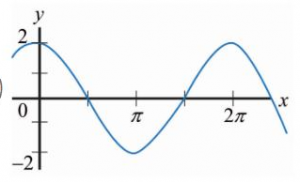
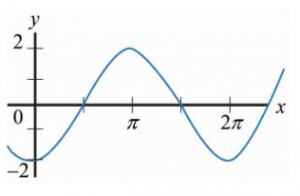
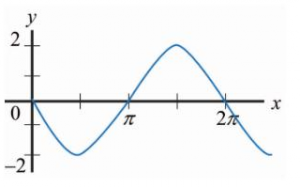
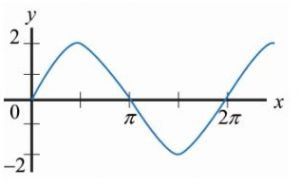
Identificar la gráfica que corresponde a la antiderivada de:

\frac{d F(x)}{d x}=2 \cos (x+2 \pi)

1. 
2. 
3. 
4. 

Solución:

Según la definición de antiderivada, el operador de integración “deshace” al operador de diferenciación. Con base en esto, procedemos a integrar en ambos miembros:

\int \frac{d F(x)}{d x} d x=\int 2 \cos (x+2 \pi) d x

F(x)=\int 2 \cos (x+2 \pi) d x

Por propiedad de la integral de una función por una constante, podemos extraer fuera al 2:

F(x)=2 \int \cos (x+2 \pi) d x

Ya que la derivada de x+2 \pi es 1, podemos aplicar integración directa:

F(x)=2 \int \cos (x+2 \pi) d(x+2 \pi)

Según las tablas de integración básicas:

  \int f(x)^{\prime} \cos [f(x)] d f(x)=\operatorname{sen}[f(x)]+C

F(x)=2 \int \cos (x+2 \pi) d(x+2 \pi)=2 \operatorname{sen}(x+2 \pi)+C

Concluimos finalmente que:

F(x)=2 \operatorname{sen}(x+2 \pi)+C

Sí suponemos que C=0

F(x)=2 \operatorname{sen}(x+2 \pi)

Según identidades trigonométricas, desplazar +2 \pi radianes a cualquiera de las funciones trigonométricas, la dejaría inalterada.

F(x)=2 \operatorname{sen}(x)

La gráfica de esta función es la del seno con amplitud 2 unidades. Comparando con las opciones que ofrece el problema, la respuesta correcta es la d).

Reactivo 2

Hallar la antiderivada de la función F(t) si \frac{d F(t)}{d t}=\frac{e^{2 t}+4}{e^{2 t}} .

1. \ln \left(e^{-2 t}+4\right)+C
2. 4 \ln \left(e^{-2 t}+4\right)+C
3. t-2 e^{-2 t}+C
4. 4 t-2 e^{-2 t}+C

Solución:

Aplicando la definición de antiderivada nos queda:

\frac{d F(t)}{d t}=\frac{e^{2 t}+4}{e^{2 t}} \rightarrow F(t)=\int \frac{e^{2 t}+4}{e^{2 t}} d t

A simple vista, parece una integral complicada, pero solo basta con aplicar algo de álgebra para simplificar al integrando.

F(t)=\int \frac{e^{2 t}+4}{e^{2 t}} d t=\int\left(1+\frac{4}{e^{2 t}}\right) d t

Aplicando ahora la propiedad del exponente negativo a \frac{4}{e^{2 t}} obtenemos:

=\int\left(1+\frac{4}{e^{2 t}}\right) d t=\int\left(1+4 e^{-2 t}\right) d t

Con la propiedad de la integral de la suma la integral queda como:

=\int d t+\int 4 e^{-2 t} d t

La primera integral es inmediata. Para la segunda, solo hay que multiplicar y dividir por -2, porque la derivada de -2 t es -2.

=\int d t-\frac{4}{2} \int(-2) e^{-2 t} d t=t-2 e^{-2 t}+C

F(t)=t-2 e^{-2 t}+C

Comparando con las opciones que ofrece el problema, la respuesta correcta es la c).

Reactivo 3

Se define Y(x)=\int\left[2 x^{3}-\frac{1}{2} x\right] d x . Si se sabe que Y(2)=10 , encontrar la función Y(x) con su constante de integración.

1. Y(x)=\frac{1}{2} x^{4}-\frac{1}{4} x^{2}+3
2. Y(x)=\frac{1}{2} x^{4}-\frac{1}{4} x^{2}+10
3. Y(x)=\frac{1}{4} x^{4}-\frac{1}{2} x^{2}+3
4. Y(x)=\frac{1}{4} x^{4}-\frac{1}{2} x^{2}+10

Solución:

Para resolver este problema, primero resolveremos la integral planteada por el enunciado. Luego, sustituiremos x=2 en el resultado igualándolo a 10 para calcular el valor respectivo de la constante de integración.

Y(x)=\int\left[2 x^{3}-\frac{1}{2} x\right] d x

Aplicamos la propiedad de la integral de la suma.

Y(x)=2 \int x^{3} d x-\frac{1}{2} \int x d x

Se emplean las fórmulas de integral de una potencia para encontrar las primitivas.

=2 \int x^{3} d x-\frac{1}{2} \int x d x=\frac{2 x^{4}}{4}-\frac{\frac{1}{2} x^{2}}{2}+c

Y(x)=\frac{1}{2} x^{4}-\frac{1}{4} x^{2}+c

Ahora, sustituimos Y(x=2)=10 .

Y(x=2)=10=\frac{1}{2}(2)^{4}-\frac{1}{4}(2)^{2}+c

10=7+C \rightarrow C=3

Finalmente:

Y(x)=\frac{1}{2} x^{4}-\frac{1}{4} x^{2}+3

Comparando con las opciones que ofrece el problema, la respuesta correcta es la a).

Reactivo 4

Encontrar la constante de integración para la función X(t)=\int 8 \operatorname{sen}(4 t+\pi) d t, \operatorname{si} X(0)=0 .

1. X(t)=2[\operatorname{sen}(4 t+\pi)+2]
2. X(t)=-2 \cos (4 t+\pi)+1
3. X(t)=2[\operatorname{sen}(4 t+\pi)+2]
4. X(t)=-2[\cos (4 t+\pi)+1]

Solución:

Para resolver este problema, obtendremos la antiderivada de la función X(t) , para luego evaluar en el punto y calcular el valor respectivo de la constante de integración en base a la condición dada X(0)=0 .

X(t)=\int 8 \operatorname{sen}(4 t+\pi) d t

Aplicamos la propiedad de la integral de una constante por una función.

X(t)=8 \int \operatorname{sen}(4 t+\pi) d t

Para poder aplicar la fórmula de la integral del seno, en el integrando debe encontrarse el diferencial del argumento del seno. Dicho diferencial es 4 d x , solo debemos multiplicar y dividir por 4.

X(t)=\frac{8}{4} \int 4 \operatorname{sen}(4 t+\pi) d t=2 \int \operatorname{sen}(4 t+\pi) d(4 t+\pi)

Finalmente.

X(t)=-2 \cos (4 t+\pi)+C

Sustituimos t=0 e igualamos la función a 0.

X(0)=0=-2 \cos (0+\pi)+C

-2(-1)+C=0 \rightarrow C=-2

X(t)=-2 \cos (4 t+\pi)-2=-2[\cos (4 t+\pi)+1]

Comparando con las opciones que ofrece el problema, la respuesta correcta es la d).

Reactivo 5

Identificar la curva correcta al hallar la constante de integración de:

F(x)=\int 4 x d x, \text { donde } F(0)=2

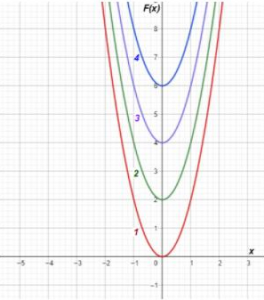
1. 1
2. 2
3. 3
4. 4

Solución:

Resolvemos la integral indicada:

F(x)=\int 4 x d x=4 \int x d x

\therefore F(x)=2 x^{2}+C

Sustituimos x=0 \operatorname{con} F(0)=2 .

F(0)=2=2(0)^{2}+C

C=2

Finalmente.

F(x)=2 x^{2}+2

Comparando con las opciones en la imagen, la gráfica correcta es la que corta al eje y en 2, ya que nuestra función vale 2 cuando x=0 . La respuesta correcta es la opción b).

Reactivo 6

Calcular \int_{0}^{1}[2 f(x)-3 g(x)] d x \text { si } \int_{0}^{1} f(x) d x=4 \text { y } \int_{0}^{1} g(x) d x=-1 .

1. 3
2. 5
3. 11
4. 24

Solución:

Para resolver este problema, comenzaremos por aplicar la propiedad de la integral de una constante por una función y la integral de la suma, para simplificar cada integrando.

\int_{0}^{1}[2 f(x)-3 g(x)] d x=2 \int_{0}^{1} f(x) d x-3 \int_{0}^{1} g(x) d x

Los valores de \int_{0}^{1} f(x) d x y \int_{0}^{1} g(x) d x los conocemos, ya que son datos dados por el problema. 4 y -1 respectivamente. Sustituyendo nos queda:

2 \int_{0}^{1} f(x) d x-3 \int_{0}^{1} g(x) d x=2(4)-3(-1)=8+3=11

Concluimos indicando que.

\int_{0}^{1}[2 f(x)-3 g(x)] d x=11

Comparando con las opciones que ofrece el problema, escogemos como respuesta correcta a la opción c).

Reactivo 7

Hallar la siguiente integral indefinida: \int(2+x) \sqrt{x} d x

1. \frac{4 x^{\frac{2}{3}}}{3}+\frac{2 x^{\frac{2}{5}}}{5}+C
2. \frac{3 x^{\frac{3}{2}}}{4}+\frac{5 x^{\frac{5}{2}}}{2}+C
3. \frac{3 x^{\frac{2}{3}}}{4}+\frac{5 x^{\frac{2}{5}}}{2}+C
4. \frac{4 x^{\frac{3}{2}}}{3}+\frac{2 x^{\frac{5}{2}}}{5}+C

Solución:

Aunque a simple vista parezca una integral atemorizante, lo que haremos es desarrollar el producto distributivo y expresar los radicales como potencias para finalmente aplicar la integral de una potencia.

\int(2+x) \sqrt{x} d x=\int 2 \sqrt{x} d x+\int x \sqrt{x} d x

=2 \int x^{\frac{1}{2}} d x+\int x x^{\frac{1}{2}} d x=2 \int d x+\int x^{1+\frac{1}{2}} d x

=2 \int x^{\frac{1}{2}} d x+\int x^{\frac{3}{2}} d x

Aplicamos la fórmula para la integral de una potencia.

=\frac{2 x^{\frac{3}{2}}}{\frac{3}{2}}+\frac{x^{\frac{5}{2}}}{\frac{5}{2}}+C=\frac{4 x^{\frac{3}{2}}}{3}+\frac{2 x^{\frac{5}{2}}}{5}+C

Concluimos que:

\int(2+x) \sqrt{x} d x=\frac{4 x^{\frac{3}{2}}}{3}+\frac{2 x^{\frac{5}{2}}}{5}+C

Comparando con las opciones que ofrece el problema, la respuesta correcta es la d).

Reactivo 8

Calcular la integral indefinida:

\int(\sqrt{2}+\sqrt{x})^{2} d x

1. 2 x-\frac{4 x \sqrt{2 x}}{3}+\frac{x^{2}}{2}+C
2. 2 x+\frac{4 x \sqrt{2 x}}{3}+\frac{x}{2}+C
3. 2 x-\frac{4 x \sqrt{2 x}}{3}+\frac{x}{2}+C
4. 2 x+\frac{4 x \sqrt{2 x}}{3}+\frac{x^{2}}{2}+C

Solución:

A simple vista, resolver la integral por fórmula es imposible, ya que no corresponde a ninguna de las formas comunes. Desarrollaremos el producto notable en el integrando para llegar a una expresión más simple con sumandos.

\int(\sqrt{2}+\sqrt{x})^{2} d x=\int(2+2 \sqrt{2 x}+x) d x

Separamos la integral.

=\int 2 d x+\int 2 \sqrt{2 x} d x+\int x d x

Resolvemos cada integral simple aplicando las fórmulas básicas correspondientes.

=2 x+\frac{4}{2} \sqrt{2} x^{\frac{3}{2}}+\frac{x^{2}}{2}+C

=2 x+\frac{4 x \sqrt{2 x}}{3}+\frac{x^{2}}{2}+C

Comparando con las opciones del reactivo, se escoge como respuesta correcta a la opción d).

Reactivo 9

Calcular la integral:

\int\left(x^{3}+4 x^{2}-\frac{3}{x}-\frac{7}{x^{2}}+1\right) d x

1. \frac{x^{4}}{4}+\frac{4 x^{3}}{3}-3 \ln x+\frac{7}{x}+x+C
2. \frac{x^{4}}{4}-\frac{4 x^{3}}{3}-3 \ln x+\frac{7}{x}+x+C
3. -\frac{x^{4}}{4}+\frac{4 x^{3}}{3}-3 \ln x+\frac{7}{x}+x+C
4. -\frac{x^{4}}{4}-\frac{4 x^{3}}{3}-3 \ln x-\frac{7}{x}-x+C

Solución:

En este caso, solo debemos aplicar la propiedad de la suma para integrales y aplicar la respectiva fórmula de integración en cada caso.

\int\left(x^{3}+4 x^{2}-\frac{3}{x}-\frac{7}{x^{2}}+1\right) d x=\int x^{3} d x+\int 4 x^{2} d x-\int \frac{3}{x} d x-\int \frac{7}{x^{2}} d x+\int d x

Se aplican las fórmulas para integrar una potencia, el inverso de  y el diferencial.

=\frac{x^{4}}{4}+\frac{4 x^{3}}{3}-3 \ln (x)-\frac{7}{x}+x+C

Comparando con las opciones, la respuesta correcta es la a).

Reactivo 10

Obtener la integral de:

\int\left(\frac{2}{\sqrt[3]{x}}+\frac{1}{x^{2}}\right) d x

1. 2 \sqrt[3]{x}-\frac{1}{x}+C
2. 3 \sqrt{x}+x+C
3. 3 \sqrt[3]{x^{2}}-\frac{1}{x}+C
4. 9 \sqrt{x}+x+C

Solución:

De nuevo, aplicamos la propiedad de la suma para integrales, luego convertimos ambos integrando radicales en potencias para finalmente aplicar la fórmula de integral de una potencia.

\int\left(\frac{2}{\sqrt[3]{x}}+\frac{1}{x^{2}}\right) d x=\int \frac{2}{\sqrt[3]{x}} d x+\int \frac{1}{x^{2}} d x

Convertimos los radicales a potencias.

=2 \int x^{-\frac{1}{3}} d x+\int x^{-2} d x

Integramos ambos términos.

=\frac{2 x^{\frac{2}{3}}}{\frac{2}{3}}-x+C=3 x^{\frac{2}{3}}-x+C

Comparando con las opciones que ofrece el problema, la respuesta correcta es la c).