Examen Simulador IPN de Cálculo integral: Ejercicios del 21 al 30

Continúa con la solución del examen simulacro de cálculo integral para que alcances un buen resultado en tu examen de admisión en el Instituto Politécnico Nacional. Vamos a resolver los ejercicios del 21 al 30.

Reactivo 21

Hallar la integral indefinida:

\int \frac{x d x}{\sqrt{x^{2}+25}}

1. \frac{1}{\sqrt{x^{2}+5^{2}}}+C
2. \frac{x^{2}}{\sqrt{x^{2}+5^{2}}}+C
3. \sqrt{x^{2}+5^{2}}+C
4. x^{2} \sqrt{x^{2}+5^{2}}+C

Solución:

En este caso, el cambio de variable se hará para la expresión de adentro del radicar, ya que en el numerador tenemos a x que es de un grado menor que el binomio cuadrático del radical.

w=x^{2}+25 \rightarrow d w=2 x d x

x d x=\frac{1}{2} d w

Aplicamos el CV.

\frac{1}{2} \int \frac{d w}{\sqrt{w}}=\frac{1}{2} \int \omega^{-1 / 2} d w

Resolvemos aplicando la fórmula de integral de una potencia.

\frac{1}{2} \int \omega^{-1 / 2} d w=\frac{1}{2} \frac{\omega^{1 / 2}}{\frac{1}{2}}+C=\sqrt{\omega}+C

Devolvemos el CV.

\sqrt{\omega}+C \sim \sqrt{x^{2}+25}+C

Finalmente.

\int \frac{x d x}{\sqrt{x^{2}+25}}=\sqrt{x^{2}+25}+C

Comparando con las opciones del problema, la respuesta correcta es la c).

Reactivo 22

Resolver la siguiente integral \int \frac{e^{\theta}}{c+a e^{\theta}} d \theta donde c y a son constantes.

1. -\frac{1}{a} \ln \left|c+a e^{\theta}\right|+C
2. \operatorname{aln}\left|c+a e^{\theta}\right|+C
3. -\operatorname{aln}\left|c+a e^{\theta}\right|+C
4. \frac{1}{a} \ln \left|c+a e^{\theta}\right|+C

Solución:

Aplicamos cambio de variable al denominador de la integral.

w=c+a e^{\theta} \rightarrow d w=a e^{\theta} d \theta

e^{\theta} d \theta=\frac{1}{a} d w

Sustituyendo.

\int \frac{e^{\theta}}{c+a e^{\theta}} d \theta \sim \frac{1}{a} \int \frac{d w}{w}

Utilizamos la fórmula de la integral de \frac{1}{w} .

\frac{1}{a} \int \frac{d w}{w}=\frac{1}{a} \ln |w|+C

Devolvemos el CV.

\frac{1}{a} \ln |w|+C \sim \frac{1}{a} \ln \left|c+a e^{\theta}\right|+C

Finalmente.

\int \frac{e^{\theta}}{c+a e^{\theta}} d \theta=\frac{1}{a} \ln \left|c+a e^{\theta}\right|+C

Comparando con las opciones que ofrece el problema, la respuesta correcta es la d).

Reactivo 23

Hallar la integral indefinida:

\int \sec ^{3}(6 x) \cdot \tan (6 x) d x

1. \frac{1}{6} \sec ^{3}(6 x)+C
2. \frac{1}{18} \sec ^{3}(6 x)+C
3. \frac{1}{18} \sec (6 x) \cdot \tan (6 x)+C
4. \frac{1}{6} \sec (6 x) \cdot \tan (6 x)+C

Solución:

Separamos el integrando para acomodar un cambio de variable. Del cálculo diferencial sabemos que:

\frac{d[\sec (x)]}{d x}=\sec (x) \tan (x)

Con base en esto, le aplicamos el cambio de variable a \sec (x) .

\int \sec ^{3}(6 x) \cdot \tan (6 x) d x=\int \sec ^{2}(6 x) \cdot \sec (6 x) \cdot \tan (6 x) d x

w=\sec (6 x)

d w=6 \sec (6 x) \operatorname{tg}(6 x) d x

\sec (6 x) \operatorname{tg}(6 x) d x=\frac{1}{6} d w

Sustituimos.

\int \sec ^{2}(6 x) \cdot \sec (6 x) \cdot \tan (6 x) d x \sim \frac{1}{6} \int w^{2} d w

Empleamos la fórmula de la integral de la potencia.

\frac{1}{6} \int w^{2} d w=\frac{1}{6} \frac{\omega^{3}}{3}+C=\frac{\omega^{3}}{18}+C

Devolviendo el CV.

\frac{\omega^{3}}{18}+C \sim \frac{\sec ^{3}(6 x)}{18}+C

Finalmente.

\int \sec ^{3}(6 x) \cdot \tan (6 x) d x=\frac{\sec ^{3}(6 x)}{18}+C

Comparando con las opciones que ofrece el problema, la respuesta correcta es la b).

Reactivo 24

Calcular la integral por partes siguiente:

\int x \ln (3 x) d x

1. \frac{x^{2}}{2}\left(\ln (3 x)-\frac{1}{2}\right)+C
2. x^{2}\left(\ln (3 x)-\frac{1}{2}\right)+C
3. x^{2} \ln (3 x)+C
4. \frac{x^{2}}{2}(\ln (3 x))+C

Solución:

El método de integración por partes se basa en un pequeño cambio de variables aplicado sobre la derivada del producto de dos funciones.

\frac{d}{d x}(f g)=g \frac{d f}{d x}+f \frac{d g}{d x} \rightarrow \int f(x) g^{\prime}(x) d x=f(x) g(x)-\int f^{\prime}(x) g(x) d x

Por simplicidad, expresaremos la fórmula de integración por partes como:

\int u d v=u v-\int v d u

Donde u será la función que conviene derivar y v la función que conviene integrar. Puedes aplicar la regla de ILATES o la regla ALPES para seleccionar la función candidata a ser u . Son reglas que funcionan en muchos casos.

Nuestra recomendación es que, no las tengas como primera opción para resolver integrales por partes. Ejercita tu propia intuición y practica mucho. Lo mejor, es verlas como herramientas, no como un paso más a seguir.

En este caso, es más que claro que la función que conviene derivar es \ln (3 x) y x la que conviene integrar, por lo tanto:

u=\ln (3 x) \quad d v=x d x

Derivamos e Integramos.

d u=\frac{3}{3 x} d x \quad v=\frac{x^{2}}{2}

Ahora, expresamos a la integral original como:

i=u v-\int v d u

i=\frac{x^{2}}{2} \ln (3 x)-\int \frac{x^{2}}{2} \cdot \frac{1}{x} d x

i=\frac{x^{2}}{2} \ln (3 x)-\frac{1}{2} \int x d x

La integral resultante es muy sencilla. Resolvemos y concluimos nuestra respuesta.

\frac{x^{2}}{2} \ln (3 x)-\frac{1}{2} \int x d x=\frac{x^{2}}{2} \ln (3 x)-\frac{1}{4} x^{2}+C

Finalmente.

\int x \ln (3 x) d x=\frac{x^{2}}{2}\left[\ln (3 x)-\frac{1}{2}\right]+C

Comparando con las opciones que ofrece el problema, la respuesta correcta es la a).

Reactivo 25

Resolver la siguiente integral indefinida:

\frac{1}{2} \int x^{2}[6 \ln x+5] d x

1. x^{3} \ln x+\frac{x^{3}}{2}+C
2. \frac{x^{3} \ln x}{2}-\frac{x^{3}}{3}+C
3. \frac{x^{3} \ln x}{3}-\frac{x^{3}}{9}+C
4. \frac{x^{3} \ln x}{4}+\frac{x^{3}}{12}+C

Solución:

Nuevamente, escogemos como u a la función con el logaritmo, es decir u=6 \ln x+5 y a d v=x^{2} .

\left\{\begin{array}{c}u=6 \ln x+5 \\d v=\frac{1}{2} x^{2}\end{array}\right.

Derivamos e integramos.

\left\{\begin{array}{c}d u=\frac{6}{x} d x \\v=\frac{1}{6} x^{3}\end{array}\right.

Ahora, expresamos a la integral original:

i=u v-\int v d u

i=\frac{1}{6} x^{3}[6 \ln x+5]-\int \frac{1}{6} x^{3} \cdot \frac{6}{x} d x

=x^{3} \ln x+\frac{5 x^{3}}{6}-\int x^{2} d x

Integramos aplicando la fórmula de la integral de la potencia.

=x^{3} \ln x+\frac{5}{6} x^{3}-\frac{x^{3}}{3}+C

=x^{3} \ln x+\frac{x^{3}}{2}+C

Comparando con las opciones que ofrece el problema, la respuesta correcta es la a).

Reactivo 26

Determinar la integral:

\int x^{2} \cos (x) d x

1. x^{2} \cos (x)+2 x \operatorname{sen}(x)-x \cos (x)+C
2. -x^{2} \operatorname{sen}(x)-2 x \cos (x)+\operatorname{xsen}(x)+C
3. x^{2} \cos (x)-2 x \operatorname{sen}(x)+x \cos (x)+C
4. x^{2} \operatorname{sen}(x)+2 x \cos (x)-\operatorname{xsen}(x)+C

Solución:

En este caso, como la derivada del coseno no se degrada, es decir, no se convierte en una función más simple al derivar, escogemos a x^{2} como u y a \cos (x) como d v , entonces:

\left\{\begin{array}{c}u=x^{2} \\d v=\cos x d x\end{array}\right.

Derivando e integrando.

\left\{\begin{array}{c}d u=2 x d x \\v=\operatorname{sen} x\end{array}\right.

Ahora, expresamos a la integral original como:

i=u v-\int v d u

i=x^{2} \operatorname{sen} x-2 \int x \operatorname{sen} x d x

Trabajamos a la segunda integral por separado.

i_{2}=2 \int x \operatorname{sen} x d x

Aplicamos integración por partes nuevamente. Seleccionamos como u a x y como d v a \operatorname{sen} x .

u=x

d v=\operatorname{sen} x d x

d u=d x

v=-\cos x

Expresamos a la segunda integral en base a la fórmula.

i_{2}=-2 x \cos x+2 \int \cos x d x

La tercera integral es inmediata, por tanto:

i_{2}=-2 x \cos x+2 \operatorname{sen} x+C

Sustituimos el resultado en la integral original.

i=x^{2} \operatorname{sen} x-2 \int \mathrm{xsen} x d x=x^{2} \operatorname{sen} x+2 x \cos x-2 \operatorname{sen} x+C

Finalmente.

\int x^{2} \cos (x) d x=x^{2} \operatorname{sen} x+2 x \cos x-2 \operatorname{sen} x+C

Comparando con las opciones que ofrece el problema, la respuesta correcta es la d).

Reactivo 27

Resolver la siguiente integral:

\int 2 \ln x^{3} d x

1. 6 x(\ln x-1)+C
2. 6 x(\ln x+1)+C
3. \frac{2}{3} x(\ln x-1)+C
4. \frac{2}{3} x(\ln x+1)+C

Solución:

La integral del logaritmo no se encuentra en las tablas de fórmulas básicas para integrales. La razón es que depende mucho de la función que lleve como argumento. Para resolverla, se emplea el método por partes.

Primero, extraemos el 2 y aplicamos la propiedad de los logaritmos: logaritmo de una potencia.

\int 2 \ln x^{3} d x=6 \int \ln (x) d x

Seleccionamos como u a \ln (x) y a d v a d x .

u=\ln (x)

d v=d x

Derivamos e integramos.

d u=\frac{1}{x} d x

v=x

Ahora, expresamos a la integral original como:

i=u v-\int v d u

i=6 x \ln (x)-6 \int x \cdot \frac{1}{x} d x=6 x \ln (x)-6 \int d x

Resolvemos esta integral inmediata:

i=6 x \ln (x)-6 x+C

Finalmente.

\int 2 \ln x^{3} d x=6 x \ln (x)-6 x+C=6 x[\ln (x)-1]+C

Comparando con las opciones que ofrece el problema, la respuesta correcta es la a).

Reactivo 28

Resolver la siguiente integral:

\int \frac{4 d u}{\left(4-u^{2}\right)^{\frac{3}{2}}}

1. \frac{4 u}{\sqrt{4-u^{2}}}+C
2. \frac{u}{4 \sqrt{4-u^{2}}}+C
3. \frac{u}{\sqrt{4-u^{2}}}+C
4. \frac{8 u}{\sqrt{4-u^{2}}}+C

Solución:

El método de integración por sustitución trigonométrica es útil para integrandos con algún factor  a^{2} \pm x^{2} o  \sqrt{a^{2} \pm x^{2}} donde no es posible aplicar cambio de variable o integración por partes.

Se basa en trasladar la expresión anterior con a y x a un triángulo mediante el teorema de Pitágoras. Luego, con las relaciones trigonométricas, la integral se transforma de algebraica a una trigonométrica que, usualmente es más simple.

Para visualizar el cambio en este caso, debemos reacomodar un poco el integrando.

\int \frac{4 d u}{\left(\sqrt{2^{2}-u^{2}}\right)^{3}}

Para este caso, a es la hipotenusa del triángulo u es un cateto y  \sqrt{a^{2}-u^{2}} es el otro, quedando de la siguiente forma:

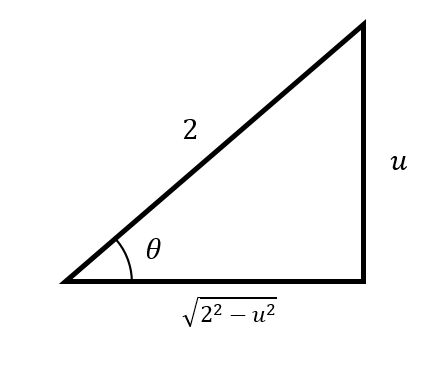
Para el caso  \sqrt{2^{2}-u^{2}} la sustitución es:

u=2 \operatorname{sen} \theta \rightarrow d u=2 \cos \theta d \theta

\sqrt{2^{2}-x^{2}}=2 \cos \theta

Aplicamos la sustitución:

\int \frac{4 d u}{\left(\sqrt{2^{2}-u^{2}}\right)^{3}} \sim 4 \int \frac{2 \cos \theta}{(2 \cos \theta)^{3}} d \theta

\int \frac{1}{\cos ^{2} \theta} d \theta=\int \sec ^{2} \theta d \theta

Empleamos la fórmula para la secante al cuadrado.

\int \sec ^{2} \theta d \theta=\operatorname{tg} \theta+C

Devolviendo el cambio de variable. A partir del triángulo:

\operatorname{tg} \theta=\frac{u}{\sqrt{4-u^{2}}}

\operatorname{tg} \theta+C \sim \frac{u}{\sqrt{4-u^{2}}}+C

Finalmente.

\int \frac{4 d u}{\left(\sqrt{2^{2}-u^{2}}\right)^{3}}=\frac{u}{\sqrt{4-u^{2}}}+C

Comparando con las opciones que ofrece el problema, la respuesta correcta es la c).

Reactivo 29

Resolver la siguiente integral:

\int \frac{d x}{\sqrt{b^{2}+x^{2}}}

1. \ln \left|\frac{\sqrt{x^{2}+b^{2}}+x}{b}\right|+C
2. \ln \left|\frac{\sqrt{x^{2}+b^{2}}+b}{x}\right|+C
3. \ln \left|\frac{\sqrt{x^{2}+b^{2}}-x}{b}\right|+C
4. \ln \left|\frac{x-\sqrt{x^{2}+b^{2}}}{b}\right|+C

Solución:

En esta integral se presenta el caso en el que en el integrando, la expresión radical corresponde a la hipotenusa del triángulo. La disposición quedaría:

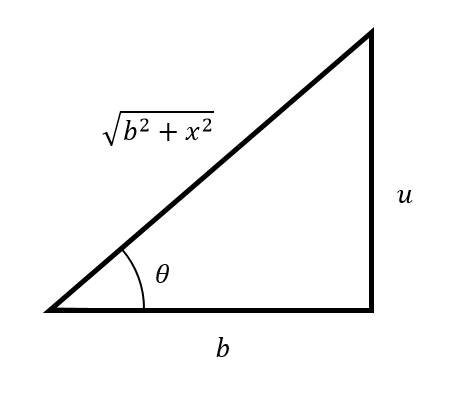
La correspondencia es:

x=b \operatorname{tg} \theta \rightarrow d x=b \sec ^{2} \theta d \theta

Sustituimos en la integral original:

\int \frac{d x}{\sqrt{b^{2}+x^{2}}} \sim \int \frac{b \sec ^{2} \theta}{b \sec \theta} d \theta=\int \sec \theta d \theta

Aplicamos la fórmula de la integral para la secante.

\int \sec \theta d \theta=\ln |\sec \theta+\operatorname{tg} \theta|+C

Del triángulo extraemos:

\operatorname{tg} \theta=\frac{x}{b}

\sec \theta=\frac{\sqrt{b^{2}+x^{2}}}{b}

Devolviendo el cambio:

\ln |\sec \theta+\operatorname{tg} \theta|+C \sim \ln \left|\frac{x}{b}+\frac{\sqrt{b^{2}+x^{2}}}{b}\right|+C

Finalmente.

\int \frac{d x}{\sqrt{b^{2}+x^{2}}}=\ln \left|\frac{x+\sqrt{b^{2}+x^{2}}}{b}\right|+C

Comparando con las opciones que ofrece el problema, la respuesta correcta es la a).

Reactivo 30

Cuál es el resultado de la integral:

\int \frac{\sqrt{4-x^{2}}}{x^{2}} d x

1. \frac{\sqrt{4-x^{2}}}{x}+\operatorname{arcsen}\left(\frac{x}{2}\right)+C
2. -\frac{\sqrt{4-x^{2}}}{x}+\operatorname{arcsen}\left(\frac{x}{2}\right)+C
3. -\frac{\sqrt{4-x^{2}}}{x}-\operatorname{arcsen}\left(\frac{x}{2}\right)+C
4. \frac{\sqrt{4-x^{2}}}{x}-\operatorname{arcsen}\left(\frac{x}{2}\right)+C

Solución:

En este caso, no es posible (a simple vista) aplicar cambio de variable y la integración por partes sería extensa. La sustitución trigonométrica acortaría enormemente la resolución. El triángulo quedaría como:

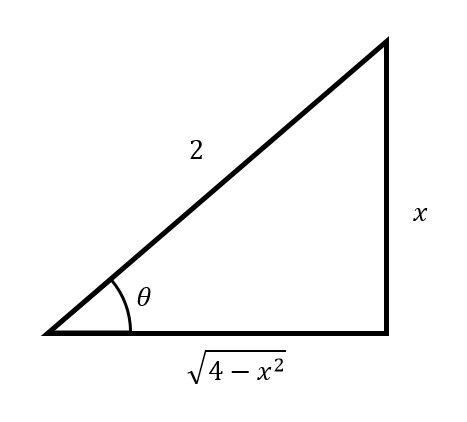
En tal caso:

x=2 \operatorname{sen} \theta \rightarrow d x=2 \cos \theta d \theta

\sqrt{2^{2}-x^{2}}=2 \cos \theta

Aplicamos la sustitución en la integral:

\int \frac{2 \cos \theta}{4 \operatorname{sen}^{2} \theta} 2 \cos \theta d \theta=\int \frac{4 \cos ^{2} \theta}{4 \operatorname{sen}^{2} \theta} d \theta=\int \frac{\cos ^{2} \theta}{\operatorname{sen}^{2} \theta} d \theta

Sustituimos por la identidad de la cotangente.

\int \cot ^{2} \theta d \theta

Ahora, la identidad para la cotangente cuadrada.

=\int\left(\csc ^{2} \theta-1\right) d \theta=\int \csc ^{2} \theta d \theta-\int d \theta

Aplicando las fórmulas de integración básicas correspondientes nos queda que:

=-\cot \theta-\theta+C

Del triángulo se sabe:

\operatorname{sen} \theta=\frac{x}{2} \rightarrow \theta=\operatorname{Arcsen}\left(\frac{x}{2}\right)

\cot \theta=\frac{\sqrt{4-x^{2}}}{x}

Sustituyendo.

-\cot \theta-\theta+C \sim-\frac{\sqrt{4-x^{2}}}{x}-\operatorname{Arcsen}\left(\frac{x}{2}\right)+C

Finalmente.

\int \frac{\sqrt{4-x^{2}}}{x^{2}} d x=-\frac{\sqrt{4-x^{2}}}{x}-\operatorname{Arcsen}\left(\frac{x}{2}\right)+C

Comparando con las opciones que ofrece el problema, la respuesta correcta es la c).