¡Hola aspirante! Has llegado a la última parte del examen simulacro de cálculo integral perteneciente al temario de matemáticas para el IPN.

Si miras en retrospectiva verás cómo has avanzado un peldaño más en el extenso temario de matemáticas del IPN, esta vez con los reactivos de cálculo integral, sin duda uno de los más difíciles de la prueba.
No olvides los puntos claves del examen y continúa estudiando para pertenecer al 20% de aspirantes aceptados en el Instituto Politécnico Nacional.
Reactivo 31
En el proceso de obtención de la siguiente integral indefinida existe un error, ¿en cuál paso se cometió?
Paso 1.
\int \frac{d y}{\left(y^{2}+4\right)^{\frac{3}{2}}}=\int \frac{d y}{\left[\left(y^{2}+4\right)^{\frac{1}{2}}\right]^{3}}
A partir del siguiente triángulo se establecen equivalencias.
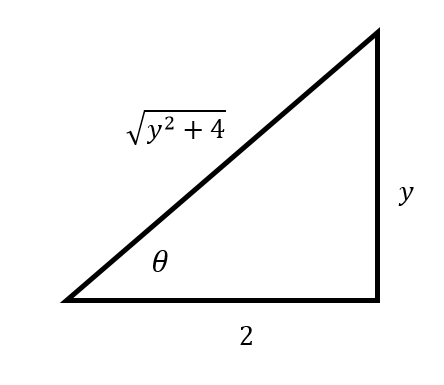
Paso 2.
\tan \theta=\frac{y}{x} \quad \sec \theta=\frac{\sqrt{y^{2}+4}}{2}
y=2 \tan \theta \quad \sqrt{y^{2}+4}=2 \sec \theta
d y=2 \sec ^{2} \theta d \theta \quad \operatorname{sen} \theta=\frac{y}{\sqrt{y^{2}+4}}
Se sustituye en la integral transformada y se simplifica.
Paso 3.
\int \frac{d y}{\left(\sqrt{y^{2}+4}\right)^{3}}=\int \frac{2 \sec ^{2} \theta d \theta}{(2 \sec \theta)^{3}}=
\frac{1}{4} \int \frac{d \theta}{\sec \theta}=\frac{1}{4} \int \cos \theta d \theta
Resolver la integral obtenida.
Paso 4.
\frac{1}{4} \int \cos \theta d \theta=\frac{1}{4} \operatorname{sen} \theta+C
Realizar nuevamente el cambio de variable.
Paso 5.
\int \frac{d y}{\left(y^{2}+4\right)^{\frac{3}{2}}}=\frac{1}{4} \frac{\sqrt{y^{2}+4}}{y}+C
- Paso 2
- Paso 3
- Paso 4
- Paso 5
Solución:
Para dar con el paso en el que se ha cometido el error, examinaremos cada una de las operaciones con detenimiento. Por la naturaleza del denominador \sqrt{y^{2}+4} la sustitución correspondiente es:
x=2 \tan \theta \text{ y } \sqrt{x^{2}+2^{2}}=2 \sec \theta
Precisamente la que se ha planteado en el primer y segundo paso.
El diferencial de x=2 \tan \theta \text { es } 2 \sec ^{2} \theta d \theta , quedando validado por completo el segundo paso. La sustitución en el tercero se hace también de forma correcta, quedando 2 \sec ^{2} \theta d \theta en lugar que d y \text{y}(2 \sec \theta)^{3} en lugar de \left(\sqrt{y^{2}+4}\right)^{3} . La simplificación posterior es también correcta.
Validado el paso 3, en el paso 4 solo queda la integral del coseno, que tiene como resultado al seno. Por último, en el paso 5 se debe devolver el cambio.
Como el resultado fue \operatorname{sen} \theta la sustitución correspondiente es \frac{y}{\sqrt{y^{2}+4}} pero en el procedimiento se ha escrito invertido. Concluimos entonces que el paso 5 es el incorrecto, el resultado debió ser:
\int \frac{d y}{\left(y^{2}+4\right)^{\frac{3}{2}}}=\frac{1}{4} \frac{y}{\sqrt{y^{2}+4}}+C
Comparando con las opciones que ofrece el problema, la respuesta correcta es la c).
Reactivo 32
La siguiente integral se puede resolver usando el método de fracciones parciales ¿Cuál será la expresión algebraica de la segunda integral?
\int \frac{3 x+6}{x^{2}-x-42} d x=\int \frac{d x}{x+6}+\int \underline{2 d x}
- x+7
- x-7
- 7-x
- -x-7
Solución:
La descomposición en fracciones parciales, es un truco algebraico que simplifica la integración de expresiones polinómicas racionales donde no es posible aplicar un cambio de variables.
Ya que solo se nos pide completar la expresión, vamos a realizar la descomposición en fracciones del integrando para escoger la respuesta correcta.
\frac{3 x+6}{x^{2}-x-42}
Parece ser el caso de un polinomio cuadrado pero, el denominador puede factorizarse como el producto de dos binomios lineales.
\frac{3 x+6}{x^{2}-x-42}=\frac{3 x+6}{(x-7)(x+6)}
Ahora el caso es el de factores lineales distintos, la descomposición quedaría como:
\frac{3 x+6}{(x-7)(x+6)}=\frac{A}{x+6}+\frac{B}{x-7}
Comparando los denominadores con el espacio faltante en el problema, concluimos que el denominador debe ser x-7 . En base a las opciones que ofrece el problema, la respuesta correcta es la b).
Reactivo 33
Para resolver la integral \int \frac{(2 x+5)}{\left(x^{2}-16\right)} d x , se emplea el método de integración por fracciones parciales, por lo que el integrando se escribe de la siguiente forma:
- \frac{A}{(x+4)}+\frac{B}{(x-4)}
- \frac{A}{(x-4)^{2}}+\frac{B}{(x+4)}
- \frac{A}{(x+4)}+\frac{B}{(x+4)^{2}}
- \frac{A}{(x-4)}+\frac{B}{(x-4)^{2}}
Solución:
Aislemos por un momento al integrando de la integral para descomponerlo en fracciones parciales.
\frac{(2 x+5)}{\left(x^{2}-16\right)}
El denominador se puede factorizar aplicando diferencia de cuadrados.
\frac{(2 x+5)}{\left(x^{2}-4^{2}\right)}=\frac{(2 x+5)}{(x-4)(x+4)}
Es el caso de factores lineales distintos, por lo que su descomposición seria:
\frac{(2 x+5)}{(x-4)(x+4)}=\frac{A}{x+4}+\frac{B}{x-4}
Comparando con las opciones que ofrece el problema, la respuesta correcta sería la a).
Reactivo 34
Al resolver la integral \int \frac{(5 x+30)}{x^{2}-3 x+2} d x por fracciones parciales ¿Cuáles son los valores de las constantes A y B?
- A=20 \text { y } B=-15
- A=-35 \text { у } B=40
- A=-40 \text { у } B=35
- A=-20 \text { y } B=15
Solución:
En este caso, solo se nos pide realizar la descomposición completa en fracciones parciales del integrando. Primero, se descompone al polinomio cuadrático del denominador en factores reales lineales.
\frac{(5 x+30)}{x^{2}-3 x+2}=\frac{(5 x+30)}{(x-2)(x-1)}
Siendo este el caso, la descomposición quedaría:
\frac{(5 x+30)}{(x-2)(x-1)}=\frac{A}{x-1}+\frac{B}{x-2}
Se pasa a multiplicar el denominador del primer miembro al segundo y se simplifican factores.
5 x+30=A(x-2)+B(x-1)
Solo queda encontrar los valores de A y B. Esto puede hacerse de dos formas: haciendo cero un término o descomponiendo para luego igualar términos. En este caso, lo haremos de la segunda manera.
5 x+30=(A+B) x-(2 A+B)
Se igualan los coeficientes de cada término.
\left\{\begin{array}{c} A+B=5 \\ -(2 A+B)=30 \end{array}\right.
Resolvemos el sistema de ecuaciones 2×2. Puedes emplear el método que quieras, la regla de Cramer 2×2 es una solución rápida.
\left\{\begin{array}{c} A+B=5 \\ -(2 A+B)=30 \end{array} \rightarrow\left|\begin{array}{cc|c} 1 & 1 & 5 \\ -2 & -1 & 30 \end{array}\right|\right.
A=\frac{\left|\begin{array}{cc} 5 & 1 \\ 30 & -1 \end{array}\right|}{\left|\begin{array}{cc} 1 & 1 \\ -2 & -1 \end{array}\right|}=-35
B=\frac{\left|\begin{array}{cc} 1 & 5 \\ -2 & 30 \end{array}\right|}{\left|\begin{array}{cc} 1 & 1 \\ -2 & -1 \end{array}\right|}=40
Finalmente.
\frac{(5 x+30)}{(x-2)(x-1)}=\frac{-35}{x-1}+\frac{40}{x-2}
Comparando con las opciones del problema, la respuesta correcta es la b).
Reactivo 35
Describir las integrales que son el resultado de descomponer en fracciones parciales la siguiente integral indefinida \int \frac{k}{(x+d)^{2}(x+f)} d x
- \int \frac{A x+B}{(x+d)^{2}} d x+\int \frac{C}{(x+f)} d x
- \int \frac{A}{(x+d)^{2}} d x+\int \frac{B}{(x+f)} d x
- \int \frac{A}{(x+d)^{2}} d x+\int \frac{B}{(x+d)} d x+\int \frac{C}{(x+f)} d x
- \int \frac{A x+B}{(x+d)^{2}} d x+\int \frac{B}{(x+d)} d x+\int \frac{C}{(x+f)} d x
Solución:
En este problema, el integrando tiene en el denominador un factor lineal repetido dos veces o de multiplicidad 2. Para ello, dicho factor repetido se descompone en n términos desde su potencia, es decir 2 hasta 1.
\frac{k}{(x+d)^{2}(x+f)}=\frac{A}{(x+d)^{2}}+\frac{B}{x+d}+\frac{C}{x+f}
Nótese que la expresión del numerador es una constante a pesar de que está elevado al cuadrado, esto es porque, a fin de cuentas, sigue siendo un factor lineal. Sustituyendo en el integrando nos queda:
\int \frac{k}{(x+d)^{2}(x+f)} d x=\int \frac{A}{(x+d)^{2}} d x+\int \frac{B}{x+d} d x+\int \frac{C}{x+f} d x
Comparando con las opciones que ofrece el problema, la respuesta correcta sería la c).
Reactivo 36
Asociar el método de integración que se puede utilizar para resolver la integral.
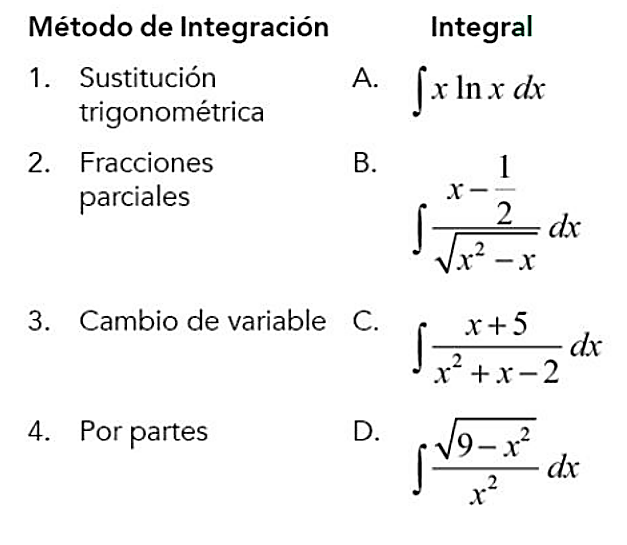
- 1B,2A,3C,4D
- 1B,2C,3A,4D
- 1D,2C,3B,4A
- 1D,2C,3A,4B
Solución:
Para responder a la pregunta, analizaremos cada una de las integrales de la columna derecha para determinar el método correcto.
Integral A.
\int x \ln x d x
Es una integral que mezcla a una función polinómica con una función logarítmica. Sin dudas, el método que se aplicaría en este caso es por partes. Por tanto 4A.
Integral B.
\int \frac{x-\frac{1}{2}}{\sqrt{x^{2}-x}} d x
Si se resuelve la resta de fracciones en el numerador, obtenemos una expresión idéntica a la derivada del argumento del radical. Con ello, podríamos entonces aplicar cambio de variable para dar con la solución. Por tanto 3B.
Integral C.
\int \frac{x+5}{x^{2}+x-2} d x
Esta integral se puede resolver aplicando fracciones parciales. El denominador es un polinomio cuadrático que se puede descomponer en dos factores lineales (x-1)(x+2) , dejando la descomposición en el caso más simple. Por tanto 2C.
Integral D.
\int \frac{\sqrt{9-x^{2}}}{x^{2}} d x
No tenemos un cambio de evidente en la integral y aplicar por partes haría la integración extensa y compleja. Sustitución trigonométrica es el método más idóneo, con el numerador \sqrt{9-x^{2}} se arma el triángulo y posteriormente la sustitución. Por tanto 1D.
Uniendo todas las soluciones nos queda: 1D, 2C, 3B, 4A. Comparando con las opciones que ofrece el problema, la respuesta correcta es la c).
Reactivo 37
Calcular el valor de:
\int_{0}^{1}\left(10 x^{4}+6 x^{2}+3\right) d x
- -2
- 2
- 5
- 7
Solución:
En este caso, resolvemos la integral como cualquier otra integral indefinida y al obtener la respuesta aplicamos el segundo teorema fundamental del cálculo:
\int_{a}^{b} f(x) d x=F(b)-F(a)
Donde F(b) \text { y } F(a) corresponden a la antiderivada de f(x) evaluada en b \text { y } a respectivamente.
\int_{0}^{1}\left(10 x^{4}+6 x^{2}+3\right) d x
Separamos la integral aplicando la propiedad de la integral de la suma y resolvemos.
=\left(10 \frac{x^{5}}{5}+\frac{6 x^{3}}{3}+3 x\right]_{0}^{1}
=\left(2 x^{5}+2 x^{3}+3 x\right]_{0}^{1}
=7-0=7
Comparando con las opciones que ofrece el problema, la respuesta correcta es la d).
Reactivo 38
Calcular la integral definida:
\int_{\frac{\pi}{4}}^{\frac{5 \pi}{4}}(\operatorname{sen} x-\cos x) d x
- \int_{\frac{\pi}{4}}^{\frac{5 \pi}{4}}(\operatorname{sen} x-\cos x) d x
- 2
- 4 \sqrt{2}
- \frac{3 \sqrt{2}}{2}
Solución:
Comenzamos por separar la integral en sumandos, para luego resolver como una indefinida y finalmente aplicar el segundo teorema fundamental del cálculo.
=\int_{\frac{\pi}{4}}^{\frac{5 \pi}{4}} \operatorname{sen} x d x-\int_{\frac{\pi}{4}}^{\frac{5 \pi}{4}} \cos x d x
Empleamos las fórmulas de integración básicas correspondientes.
\left.=-\cos x]_{\frac{\pi}{4}}^{\frac{5 \pi}{4}}-\operatorname{sen} x\right]_{\frac{\pi}{4}}^{\frac{5 \pi}{4}}
Evaluamos.
=-\cos \frac{5 \pi}{4}+\cos \frac{\pi}{4}-\operatorname{sen} \frac{5 \pi}{4}+\operatorname{sen} \frac{\pi}{4}
=2 \sqrt{2}
Finalmente.
\int_{\frac{\pi}{4}}^{\frac{5 \pi}{4}}(\operatorname{sen} x-\cos x) d x=2 \sqrt{2}
Comparando con las opciones que ofrece el problema, la respuesta correcta es la opción a).
Reactivo 39
En el cálculo del valor de la siguiente integral definida existe un error ¿en cuál paso está el error?
Paso 1.
\int_{-3}^{3} e^{\frac{1}{3} x} d x
Paso 2.
3 \int_{-3}^{3} \frac{1}{3} e^{\frac{1}{3} x} d x
Paso 3.
\left.3 e^{\frac{1}{3} x}\right|_{-3} ^{3}
Paso 4.
3 e+3 e^{-1}
Paso 5.
3\left(e+\frac{1}{e}\right)
- Paso 1
- Paso 2
- Paso 3
- Paso 4
Solución:
Para encontrar el paso incorrecto, examinemos cada una de las operaciones efectuadas para resolver la integral. En el paso 2 solo se multiplica y divide por 3 para establecer el diferencial de \frac{1}{3} x y aplicar de forma directa la fórmula de integración correspondiente.
En el paso 3, se obtiene la primitiva de la función integrando, la cual es correcta. Solo falta evaluar.
\left.3 e^{\frac{1}{3} x}\right|_{-3} ^{3}=3\left[e-e^{-1}\right]
Si comparamos con el paso 4, nuestra respuesta difiere por el signo menos. El paso 4 es el incorrecto porque el segundo TFC establece que:
\int_{a}^{b} f(x) d x=F(b)-F(a)
Comparando con las opciones que ofrece el problema, la respuesta correcta es la d).
Reactivo 40
La solución de la \int_{1}^{4}(1)^{e} d x es:
- e
- 1
- 3
- 0
Solución:
Esta integral es sencilla de resolver. Recordemos que el 1 elevado a cualquier cantidad es siempre igual a 1, por lo que nuestra integral se convierte en:
\left.\int_{1}^{4}(1)^{e} d x=\int_{1}^{4} d x=x\right]_{1}^{4}
Evaluando nos queda que:
\int_{1}^{4}(1)^{e} d x=4-1=3
Comparando con las opciones que ofrece el problema, la respuesta correcta es la c).

