Simulacro examen UNAM | 50 reactivos de Matemáticas Parte 2

Vamos con la solución de la segunda parte de los reactivos del simulador real de matemáticas, como preparación al examen de ingreso a la UNAM.

[no_toc]

Matemáticas muchas veces se entiende como una asignatura de solo fórmulas y despejes, pero en ella yacen los modelos para comprender el mundo que nos rodea.

Simulador de Matemáticas UNAM

Continuamos resolviendo los siguientes reactivos del 31 al 40 de matemáticas en el simulador real de matemáticas para la UNAM. Recuerda tomar descansos entre grupos de ejercicios, esto también forma parte del proceso de aprendizaje.

Reactivo 31

Calcule el dominio de la siguiente función logarítmica:

g\left(x\right)={\mathrm{log}}_{3}\left(\frac{x+2}{{x}^{2}+4}\right)

1. x\in \left(-\infty , 2\right)
2. x\in \left(-2, 2\right)
3. x\in \left(-2, \infty \right)
4. x\in R

Solución:

En este caso, la función principal es el logaritmo de base 3, cuya restricción es que su argumento \frac{x+2}{{x}^{2}+4} sea siempre mayor que cero.

\frac{x+2}{{x}^{2}+4}>0

Podemos simplificar el cálculo, ya que el denominador {x}^{2}+4 siempre arroja valores positivos. Esto reduce las condiciones de estudio: \frac{\left(+\right)}{\left(+\right)}=+ y \frac{\left(-\right)}{\left(-\right)}=+ , solo la primera.

x+2>0\wedge {x}^{2}+4>0

Solo resolvemos para x+2>0 , porque {x}^{2}+4>0 se cumple en todos los reales.

x+2>0\to x>-2

Interceptando:

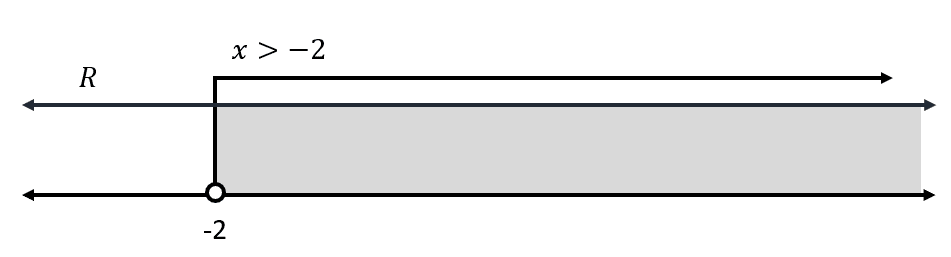
El dominio de la función g\left(x\right) son todos los reales mayores que -2.

\mathrm{D}\mathrm{o}\mathrm{m}\left(g\right)=x\in \left(-2, \infty \right)

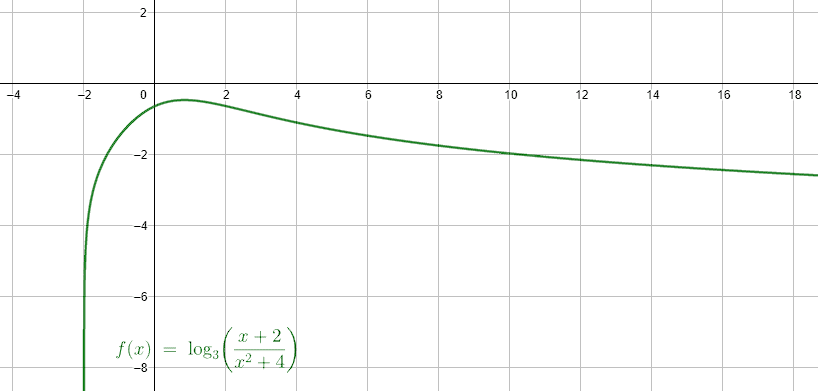
Indicamos la c) como respuesta correcta.

Si tienes dudas sobre el proceso de admisión ingresa a la convocatoria de la UNAM y conoce los pasos del registro.

Reactivo 32

Identifique el codominio de la función y={2}^{-x} .

1. y\in \left(-\infty , \infty \right)
2. y\in \left(-\infty , 0\right)
3. y\in \left(-2, 2\right)
4. y\in \left(0, \infty \right)

Solución:

El codominio o rango de una función, es el conjunto de valores que puede tomar la variable dependiente y al momento de sustituir valores en la variable independiente x .

• Cuando sustituimos un valor positivo en x , tenemos al 2 elevado a un número negativo, lo que arroja un resultado positivo que tiende a cero cuando x tiende a +\infty .
• Cuando sustituimos un valor negativo en x , nos queda el 2 elevado a un número positivo, resultando en un número positivo que siente a infinito cuando x tiende a -\infty .

Con este análisis, podemos concluir que el codominio de y={2}^{-x} es toda y mayor que cero.

\mathrm{R}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{o}\left(y\right)=y\in \left(0, \infty \right)

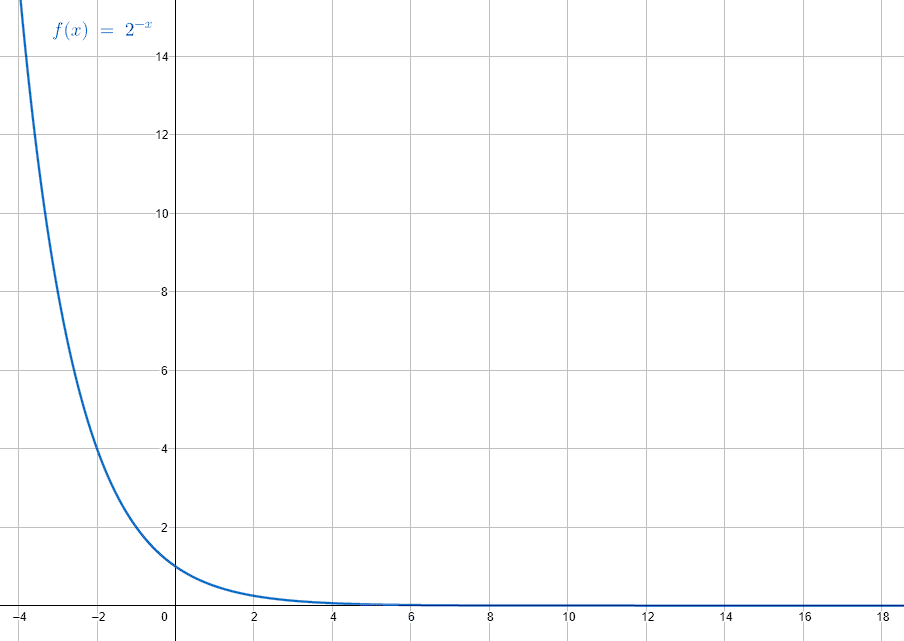
La respuesta correcta es la d).

Reactivo 33

Calcule la distancia entre los puntos A\left(1, -2\right) y B\left(2, 4\right) .

1. d\left(A,B\right)=\sqrt{37}
2. d\left(A,B\right)=\sqrt{40}
3. d\left(A,B\right)=\sqrt{35}
4. d\left(A,B\right)=\sqrt{36}

Solución:

Empleamos la ecuación de distancia entre dos puntos en el plano:

d\left(A, B\right)=\sqrt{{\left({x}_{b}-{x}_{a}\right)}^{2}+{\left({y}_{b}-{y}_{a}\right)}^{2}}

Sustituimos los valores de las coordenadas.

d\left(A, B\right)=\sqrt{{\left(2-1\right)}^{2}+{\left(4+2\right)}^{2}}=\sqrt{{1}^{2}+{6}^{2}}=\sqrt{37}

d\left(A, B\right)\approx 6.0827

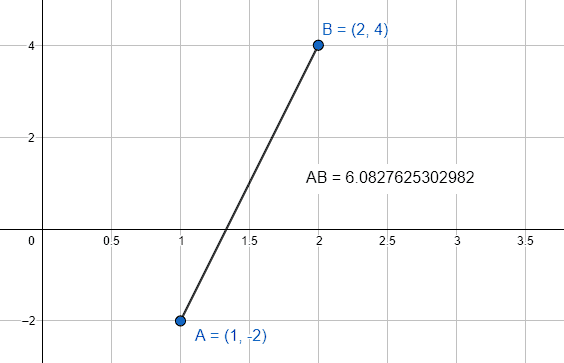
Seleccionamos al inciso a) como respuesta correcta.

Lista completa de carreras de la UNAM

Reactivo 34

Obtenga la ecuación explícita de la recta que corta a los ejes coordenados en x=2 y y=4 .

1. y=4-2x
2. y=2-4x
3. y=4+2x
4. y=2+4x

Solución:

Para resolver este problema, empleamos la ecuación simétrica de la recta:

\frac{x}{a}+\frac{y}{b}=1

Donde a y b son los cortes de la recta con los ejes x y y respectivamente. Sustituimos.

\frac{x}{2}+\frac{y}{4}=1

Para obtener la ecuación explícita y=b+mx , debemos linealizar la ecuación simétrica. Multiplicamos ambos miembros por 4.

4\left(\frac{x}{2}+\frac{y}{4}\right)=4\to 2x+y=4

Despejando nos queda:

y=4-2x

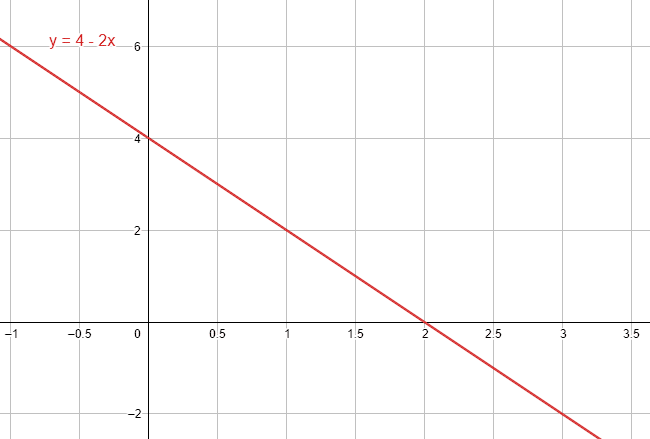
La respuesta correcta es la a).

Reactivo 35

Obtenga la ecuación explícita de la recta que es perpendicular a y=2x+1 y que pasa por el punto P\left(1, 2\right) .

1. y=5-x
2. y=\frac{1}{2}-\frac{5}{2}x
3. y=\frac{5}{2}-\frac{1}{2}x
4. y=\frac{5}{2}+\frac{1}{2}x

Solución:

La condición de perpendicularidad entre dos rectas nos dice que: la pendiente {m}_{a} de la recta a es igual a -\frac{1}{{m}_{b}} , donde {m}_{b} es la pendiente de la recta b .

Calculamos la pendiente de la recta solicitada.

{m}_{a}=-\frac{1}{{m}_{b}}=-\frac{1}{2}

Sustituimos {m}_{a} y al punto en la ecuación punto pendiente.

y-2=-\frac{1}{2}\left(x-1\right)

Simplificando:

y=2-\frac{1}{2}x+\frac{1}{2}

y=\frac{5}{2}-\frac{1}{2}x

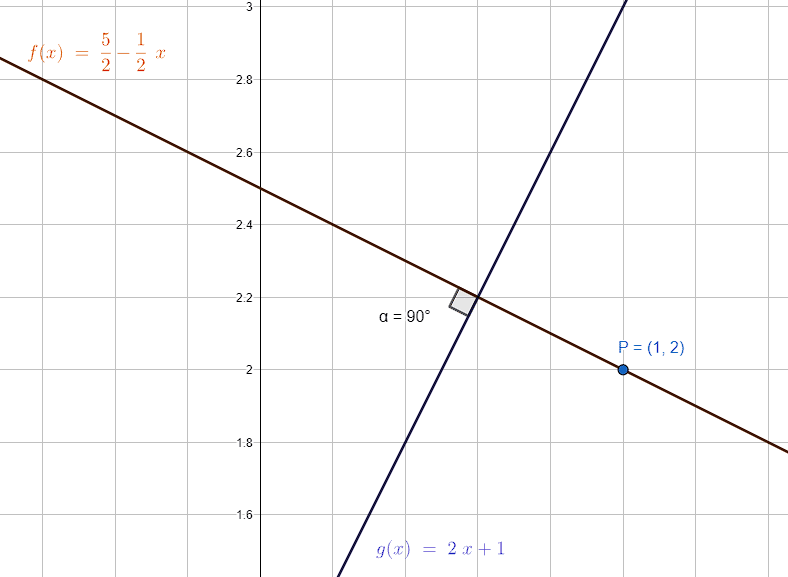
Seleccionamos como respuesta correcta al inciso c).

Reactivo 36

Determine las coordenadas del punto que divide en partes iguales al segmento cuyos extremos son A\left(-4, 5\right) y B\left(5, -6\right) .

1. {P}_{M}=\left(1, -\frac{1}{2}\right)
2. {P}_{M}=\left(-\frac{1}{2}, -\frac{1}{2}\right)
3. {P}_{M}=\left(\frac{1}{2}, \frac{1}{2}\right)
4. {P}_{M}=\left(\frac{1}{2}, -\frac{1}{2}\right)

Solución:

Para calcular el punto que divide en partes iguales a un segmento, empleamos la siguiente expresión:

{P}_{M}=\left(\frac{{x}_{a}+{x}_{b}}{2}, \frac{{y}_{a}+{y}_{b}}{2}\right)

Sustituimos las coordenadas:

{P}_{M}=\left(\frac{-4+5}{2}, \frac{5-6}{2}\right)

{P}_{M}=\left(\frac{1}{2}, -\frac{1}{2}\right)

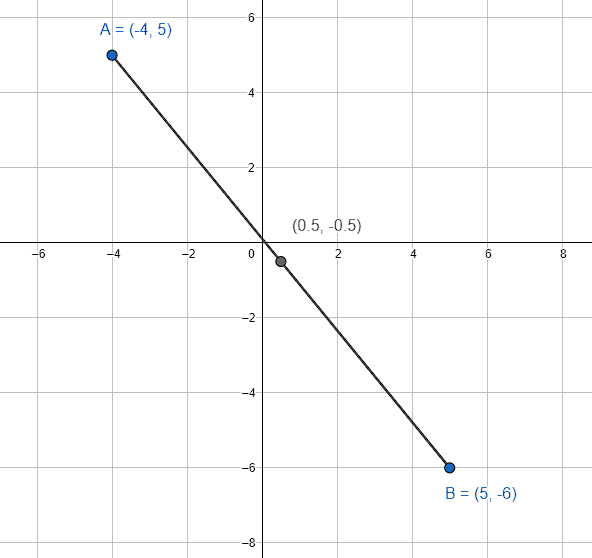
La respuesta correcta es el inciso d).

Conoce todos los temas de la guía de estudios de la UNAM

Reactivo 37

Obtenga la ecuación general de la parábola con eje focal vertical, cuyo vértice es \left(0, -1\right) y pasa por el punto \left(3, 4\right) .

1. y={x}^{2}-1
2. y=\frac{5}{9}{x}^{2}-1
3. y={x}^{2}-\frac{5}{9}
4. y=\frac{5}{9}{x}^{2}+1

Solución:

Para encontrar la ecuación general de la parábola, debemos sustituir el vértice y el lado recto en la ecuación ordinaria correspondiente. En este caso, nos dicen que el eje focal es vertical, por tanto, la ecuación ordinaria es:

y-k=4p{\left(x-h\right)}^{2}

Parábola que abre hacia arriba o hacia abajo.

Ahora, tenemos las coordenadas h, k del centro, pero no el lado recto p .

y+1=4p{\left(x-0\right)}^{2}\to y+1=4p{x}^{2}

En contraposición, el enunciado nos indica un punto por el que pasa la parábola. Si sustituimos este punto y el vértice, podemos calcular a p .

4+1=4p{\left(3\right)}^{2}\to 4p=\frac{5}{9}

Sustituyendo a 4p nos queda:

y=\frac{5}{9}{x}^{2}-1

Sustituimos x=3 para comprobar el resultado.

y=\frac{5}{9}{\left(3\right)}^{2}-1=5-1=4

Graficando la parábola:

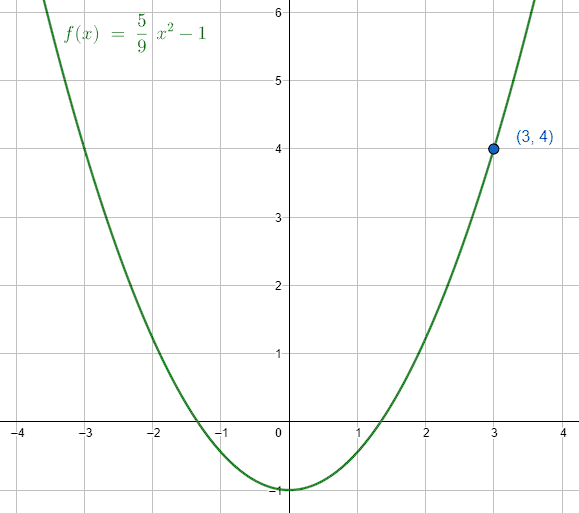
La respuesta correcta es el inciso b).

Reactivo 38

Calcule las coordenadas del vértice de la parábola, cuyo lugar geométrico está descrito por: 0={x}^{2}+x-y-1 .

1. \left(\frac{1}{2},\frac{5}{4}\right)
2. \left(-\frac{1}{2},\frac{5}{4}\right)
3. \left(\frac{1}{2},-\frac{5}{4}\right)
4. \left(-\frac{1}{2},-\frac{5}{4}\right)

Solución:

El enunciado nos indica la ecuación de la parábola en la forma general, debemos aplicar completar cuadrados para obtener la forma ordinaria y de allí extraer el vértice.

Comenzamos despejando la y .

y={x}^{2}+x-1

Al completar cuadrados, aplicamos en sentido inverso el producto notable:

{\left(a\pm b\right)}^{2}={a}^{2}\pm 2ab+{b}^{2}

El término x puede escribirse como 2\cdot \frac{1}{2}\cdot x .

y={x}^{2}+2\cdot \frac{1}{2}\cdot x-1

Si comparamos con el producto notable, a=x y b=\frac{1}{2} . Sumamos y restamos el cuadrado de \frac{1}{2} .

y={x}^{2}+2\cdot \frac{1}{2}\cdot x-1+\frac{1}{4}-\frac{1}{4}

Agrupamos.

y=\left({x}^{2}+2\cdot \frac{1}{2}\cdot x+\frac{1}{4}\right)-\frac{1}{4}-1={\left(x+\frac{1}{2}\right)}^{2}-\frac{5}{4}

y+\frac{5}{4}={\left(x+\frac{1}{2}\right)}^{2}

Concluimos que las coordenadas del vértice son:

\left(h, k\right)=\left(-\frac{1}{2},-\frac{5}{4}\right)=\left(-0.5, -1.25\right)

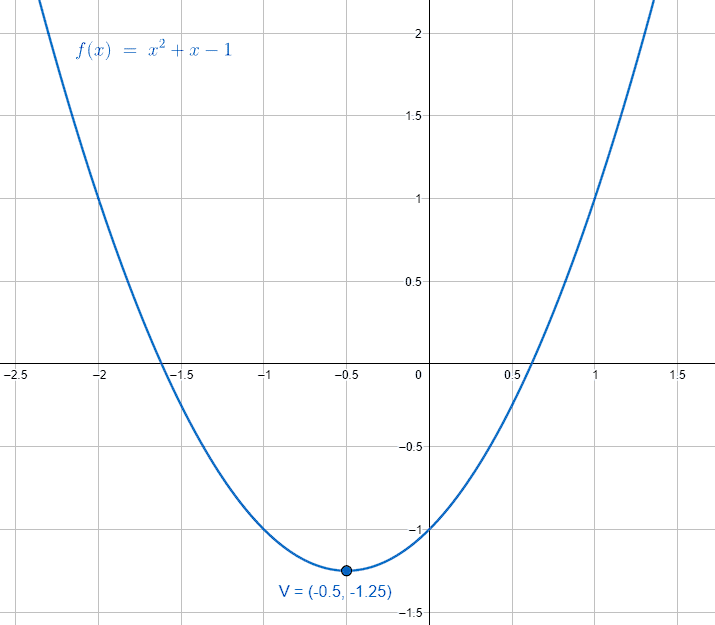
Concluimos que la respuesta correcta es el inciso d).

Reactivo 39

Determine las coordenadas del foco de la parábola:

y+1=-2{\left(x-1\right)}^{2}

1. f\left(1, -\frac{3}{2}\right)
2. f\left(1, \frac{3}{2}\right)
3. f\left(-1, -\frac{3}{2}\right)
4. f\left(-1, \frac{3}{2}\right)

Solución:

El foco de una parábola con eje focal paralelo al eje de las y (como en este caso), se encuentra en el punto \left(h, k\pm p\right) . Si la parábola abre hacia arriba p va positivo, en caso contrario, negativo.

Nuestra parábola abre hacia abajo, debido al signo negativo en el 2, por tanto, la ecuación a utilizar en este caso es:

f\left(h, k-p\right)

Calculamos a p como:

-4p=-2\to p=\frac{1}{2}

Sustituimos las coordenadas del vértice \left(1, -1\right) y el lado recto p=\frac{1}{2} .

f\left(1, -1-\frac{1}{2}\right)=f\left(1, -\frac{3}{2}\right)

Gráficamente obtenemos:

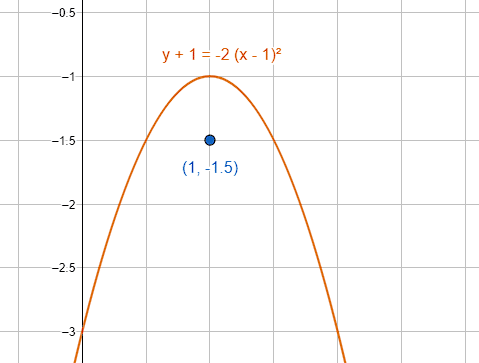
La respuesta correcta es el inciso a).

Lista de aciertos necesarios para quedar en la UNAM

Reactivo 40

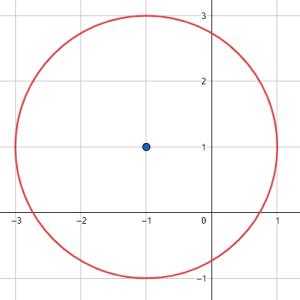
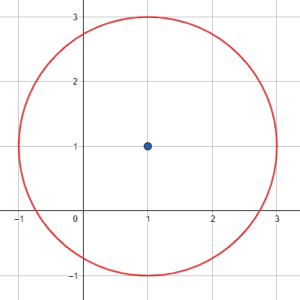
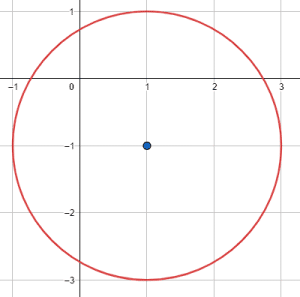
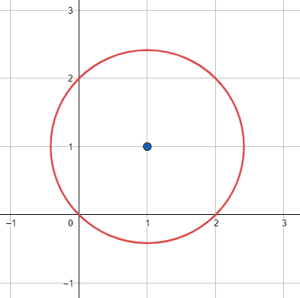
¿Cuál de las siguientes circunferencias tiene radio igual a \sqrt{2} y centro en el punto \left(1, 1\right) ?

1. 
2. 
3. 
4. 

Solución:

Para seleccionar la respuesta correcta, comencemos por identificar qué opciones se encuentran centradas en el punto \left(1, 1\right) : la b) y la d). Descartamos del análisis las otras dos opciones. Solo nos queda comprobar el radio, midiendo la distancia desde el centro hasta un punto de la circunferencia.

Radio de la circunferencia b.

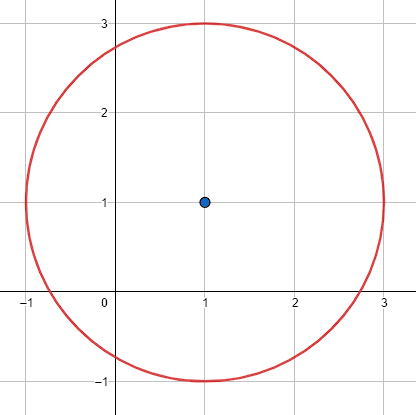
Seleccionamos como punto de la circunferencia a \left(-1, 1\right) .

r=\sqrt{{\left(-1-1\right)}^{2}+{\left(1-1\right)}^{2}}=\sqrt{4}=2

Descartamos la circunferencia b.

Radio de la circunferencia c.

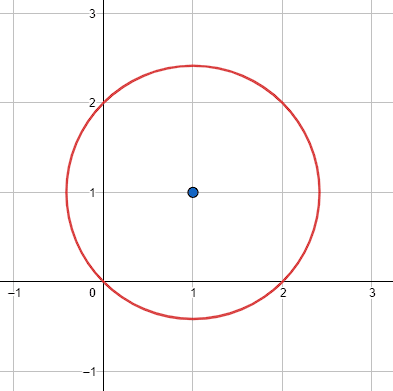
Seleccionamos al punto \left(0, 2\right) .

r=\sqrt{{\left(1-0\right)}^{2}+{\left(1-2\right)}^{2}}=\sqrt{1+1}=\sqrt{2}

Concluimos que la respuesta correcta es el inciso d).