¿Vas a presentar el examen de ingreso a la UNAM en alguna de las carreras del área 3? En este tutorial vamos a resolver 24 reactivos de la guía de matemáticas correspondiente al área de ciencias sociales.

El área 3 correspondiente a ciencias sociales abarca 9 materias, de las cuales 24 reactivos son de matemáticas, y 28 corresponden a historia universal y de México.
La licenciatura en derecho es parte de las carreras que tienen mayor cantidad de rechazo, puedes consultar la lista de carreras más difíciles en la UNAM.
Estructura examen área 3
El examen de la UNAM tiene un total de 120 reactivos, y un tiempo de 3 horas pares contestarlo en su totalidad, por lo que es muy importante que practiques y midas el tiempo para asegurarte de que no se te acaben los minutos disponibles el día del examen.
Consulta el temario completo del área 3 con la Guía UNAM vigente.
Durante el examen deberás responder reactivos de 9 materias distintas, por lo que es importante que tomes en cuenta que debes estudiar todas y cada una de ellas previo a tu prueba de admisión a la universidad.
Estructura examen de la UNAM para el área 3
| Materia | Reactivos |
| Español | 18 |
| Matemáticas | 24 |
| Física | 10 |
| Química | 10 |
| Biología | 10 |
| Historia universal | 14 |
| Historia de México | 14 |
| Literatura | 10 |
| Geografía | 10 |
| Total | 120 |
Temario matemáticas UNAM área 2
El Área 3 (ciencias sociales) incluye casi todos los temas de matemáticas que cursaste durante el bachillerato. Si no conoces para registrarte al examen te recomiendo que revises la convocatoria de la UNAM.
Estos son los temas que tienes que estudiar:
- Operaciones con números reales, complejos y expresiones algebraicas
- Números reales
- Suma y resta
- Multiplicación y división
- Raíces y potencias con exponente racional
- Números complejos
- Suma y resta
- Multiplicación
- Expresiones algebraicas
- Suma y resta
- Multiplicación y división
- Raíces y potencias con exponente racional
- Operaciones con radicales
- Números reales
- Productos notables y factorización
- Binomio de Newton a+bn, n ∈N
- Teorema del residuo y del factor
- Simplificación de fracciones algebraicas
- Operaciones con fracciones algebraicas
- Ecuaciones
- Ecuación, identidad y propiedades de la igualdad
- Ecuaciones de primer grado
- Ecuaciones de segundo grado
- Desigualdades
- Desigualdad de primer grado en una variable y sus propiedades
- Sistemas de ecuaciones
- Sistemas de dos ecuaciones lineales con dos incógnitas
- Métodos de solución
- Sistemas de tres ecuaciones lineales con tres incógnitas
- Métodos de solución (Regla de Cramer)
- Sistemas de dos ecuaciones lineales con dos incógnitas
- Funciones algebraicas
- Dominio, contradominio y regla de correspondencia
- Rango o imagen
- Gráfica
- Implícitas y explícitas
- Crecientes y decrecientes
- Continuas y discontinuas
- Álgebra de funciones
- Trigonometría
- Trigonometría básica
- Medida de un ángulo (conversión de grados a radianes y de radianes a grados)
- Razones trigonométricas
- Resolución de triángulos rectángulos
- Ley de los Senos y Ley de los Cosenos
- Resolución de triángulos oblicuángulos
- Razones trigonométricas para un ángulo en cualquier cuadrante. Fórmulas de reducción
- Funciones trigonométricas
- El círculo trigonométrico
- Funciones trigonométricas directas
- Dominio y rango
- Periodo y amplitud
- Desfasamiento
- Asíntotas de la gráfica
- Trigonometría básica
- Funciones exponenciales y logarítmicas
- Dominio y rango
- Gráficas y asíntotas
- Recta
- Distancia entre dos puntos
- Coordenadas de un punto que divide a un segmento de acuerdo con una razón dada
- Pendiente de una recta
- Formas de la ecuación de la recta y su gráfica
- Condiciones de paralelismo y perpendicularidad
- Distancia de un punto a una recta
- Ecuaciones de las medianas, mediatrices y alturas de un triángulo. Puntos de intersección (ortocentro, circuncentro y baricentro)
- Circunferencia
- Circunferencia como lugar geométrico
- Formas ordinarias (canónica) y general de la ecuación de la circunferencia con centro en el origen
- Ecuación de la circunferencia con centro en (h, k) en las formas ordinaria y general
- Elementos de una circunferencia
- Parábola
- Parábola como lugar geométrico
- Formas ordinaria y general de la ecuación de la parábola cuando el vértice está en el origen y el eje focal coincide con alguno de los ejes coordenados
- Formas ordinaria y general de la ecuación de la parábola cuando el vértice está en un punto cualquiera del plano y eje focal paralelo a alguno de los ejes coordenados
- Elementos de una parábola
- Elipse
- Elipse como lugar geométrico
- Relación entre los parámetros a, b y c
- Formas ordinaria y general de la ecuación de la elipse con centro en el origen y eje focal sobre alguno de los ejes coordenados
- Formas ordinaria y general de la ecuación de la elipse con centro fuera del origen y eje focal paralelo a alguno de los ejes coordenados
- Elementos de una elipse
- Hipérbola
- Hipérbola como lugar geométrico
- Relación entre los parámetros de la hipérbola a, b y c
- Formas ordinaria y general de la ecuación de la hipérbola con centro en el origen y eje focal sobre alguno de los ejes coordenados
- Formas ordinaria y general de la ecuación de la hipérbola con centro fuera del origen y eje focal paralelo a alguno de los ejes coordenados
- Elementos de una hipérbola
- Ecuación general de segundo grado
- Las cónicas
- Ecuación general de segundo grado
- Criterios para identificar a la cónica que representa una ecuación de segundo grado
- Traslación de ejes
¿Cómo resolver el simulacro del área 3?
Al momento de resolver un examen simulacro es importante que tomes en cuenta que se trata de un ejercicio que tiene el principal objetivo de poner a prueba tus conocimientos, está bien equivocarse aquí, lo importante es que tengas un panorama claro sobre tu nivel de conocimientos.
Consulta la oferta académica completa: Lista completa de licenciaturas de la UNAM
5 recomendaciones para antes de resolverlo:
- Mide tus tiempos (puedes usar el cronómetro de tu celular).
- Toma notas sobre los ejercicios que se te dificulten más.
- Intenta resolverlo por tu cuenta antes de consultar la solución.
- Evita cualquier tipo de distracción.
- Una vez que termines inténtalo de nuevo en unos días para medir tu avance.
En cada reactivo hemos indicado el tema para que no batalles en identificarlo, ahora sí, comenzamos…
Reactivo 1: Operaciones aritméticas
El resultado de 0.1709-2.91+1.1783 es:
- -4.1512
- -1.6592
- -4.2592
- -1.5608
Solución:
Para encontrar el resultado correcto, debemos resolver las sumas y restas con decimales de la expresión. Comencemos por 0.1709-2.91 , a 0.1709 de debemos quitar 2.91 , alineamos el punto decimal de ambas cantidades al escribir una encima de otra.
Para facilitar el proceso de resta, se escribe 2.91 y luego el 0.1709 . Al resultado se le cambia el signo.
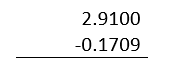
Ahora, restamos de derecha a izquierda los números que se encuentran en la misma columna, pidiendo prestado o “acarreando” al de un lado si es necesario.
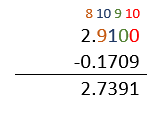
Cambiando el signo al resultado obtenemos que: 0.1709-2.91=-2.7391 . Las operaciones quedan como:
-2.7391+1.1783=1.1783-2.7391
Aplicamos el mismo procedimiento para restar ambos números.
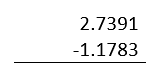
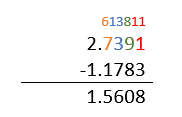
Cambiamos de signo porque invertimos las cantidades de lugar y nos queda:
1.1783-2.7391=-1.5608
Comparando el resultado con las opciones, concluimos que la respuesta correcta está en el inciso D.
Reactivo 2: Cociente de dos números
Un auto viaja a 50.4 kilómetros con 6.3 litros de gasolina. ¿Cuánto fue su rendimiento de kilómetros recorridos por litro de gasolina?
- 8\frac{km}{L}
- 9\frac{km}{L}
- 8.5\frac{km}{L}
- 9.5\frac{km}{L}
Solución:
El problema solicita que calculemos el cociente entre los 50.4 kilómetros recorridos y los 6.3 litros de gasolina que consumió el automóvil durante el viaje. En tal caso 50.4 será el dividendo y 6.3 el divisor.
![]()
Ya que los números son decimales, corremos la coma a la derecha la misma cantidad de espacios hasta que desaparezca. Si es necesario, se completa con cero.
![]()
Intentamos con el 8.
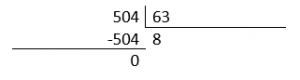
Concluimos que el auto tuvo un rendimiento de \frac{50.4 km}{6.3 L}=8\frac{km}{L} .
Seleccionamos como respuesta correcta la opción A.
Conoce los puntos necesarios por carrera para ingresar a la UNAM.
Reactivo 3: Producto notable
Desarrolla el binomio (x-y{)}^{2}
- {x}^{2}-{y}^{2}
- {x}^{2}+{y}^{2}
- {x}^{2}-2xy+{y}^{2}
- {x}^{2}+2xy+{y}^{2}
Solución:
Para encontrar el desarrollo del binomio al cuadrado tenemos dos opciones: realizar el producto entre binomios (x-y{)}^{2}=\left(x-y\right)\left(x-y\right) o aplicar producto notable. Debido a la rapidez, la mejor opción es aplicar producto notable.
{\left(a\pm b\right)}^{2}={a}^{2}\pm 2ab+{b}^{2}
En este caso a=x y b=y .
(x-y{)}^{2}={x}^{2}-2xy+{y}^{2}
Comparando el resultado con las opciones, escogemos como correcto al inciso C.
Reactivo 4: Factorización de expresiones racionales
Factoriza la siguiente operación algebraica
\frac{\left({x}^{2}-7x+12\right)}{\left({x}^{2}-16\right)(x-3)}
- \frac{1}{x-3}
- \frac{1}{x+4}
- \frac{x-3}{x+4}
- \frac{x-4}{x-3}
Solución:
Para poder simplificar elementos del numerador con elementos del denominador, es necesario expresar todo como el producto de factores primos (irreducibles). En este caso, solo hay dos expresiones que se pueden factorizar: {x}^{2}-7x+12 y {x}^{2}-16 .
En la primera, podemos aplicar la fórmula de segundo grado o factorización de la forma {x}^{2}+bx+c . Por simplicidad, nos favorece la segunda opción. Debemos encontrar dos números que sumados den -7 y multiplicados 12, ellos son: -3 y -4.
{x}^{2}-7x+12=\left(x-3\right)\left(x-4\right)
La expresión {x}^{2}-16 , puede factorizarse aplicando diferencia de cuadrados.
{x}^{2}-16={x}^{2}-{4}^{2}=\left(x+4\right)\left(x-4\right)
Sustituimos todo en la fracción original.
\frac{\left({x}^{2}-7x+12\right)}{\left({x}^{2}-16\right)(x-3)}=\frac{\left(x-3\right)\left(x-4\right)}{\left(x+4\right)\left(x-4\right)\left(x-3\right)}
Se simplifican x-3 y x-4 .
\frac{\left(x-3\right)\left(x-4\right)}{\left(x+4\right)\left(x-4\right)\left(x-3\right)}=\frac{1}{x+4}
Finalmente:
\frac{\left({x}^{2}-7x+12\right)}{\left({x}^{2}-16\right)(x-3)}=\frac{1}{x+4}
Concluimos seleccionando como correcta la opción B.
Reactivo 5: Ecuaciones lineales
La solución de la ecuación \frac{x}{4}+1=\frac{x}{2} es:
- x=\frac{1}{2}
- x=\frac{1}{4}
- x=4
- x=8
Solución:
Debemos despejar a x para encontrar el valor numérico que satisface a la ecuación. Iniciamos agrupando en el primer miembro las x y al segundo miembro los términos independientes.
\frac{x}{2} pasa restando al primer miembro y 1, restando también, al segundo miembro.
\frac{x}{4}+1=\frac{x}{2}\to \frac{x}{4}-\frac{x}{2}=-1
Multiplicamos todo por -1.
\frac{x}{4}-\frac{x}{2}=-1\to \frac{x}{2}-\frac{x}{4}=1
Realizamos la resta de fracciones.
\frac{x}{2}-\frac{x}{4}=1\to \frac{4x-2x}{8}=1
\frac{2x}{8}=1
Simplificamos y despejamos.
\frac{x}{4}=1
\therefore x=4
La solución de la ecuación \frac{x}{4}+1=\frac{x}{2} es x=4 .
Concluimos al indicar como correcta la opción C.
Reactivo 6: Ecuaciones lineales
Resuelve la siguiente ecuación.
5+\frac{x}{x+2}=1
- -\frac{8}{5}
- \frac{5}{8}
- -\frac{5}{8}
- \frac{8}{5}
Solución:
Encontrar la solución de la ecuación, pasa por despejar a x y calcular su valor numérico, aplicando las propiedades de la igualdad. Comencemos por pasar el 5 restando al segundo miembro.
5+\frac{x}{x+2}=1\to \frac{x}{x+2}=1-5\to \frac{x}{x+2}=-4
Ahora, multiplicamos la igualdad por x+2 .
\frac{x}{x+2}\left(x+2\right)=-4\left(x+2\right)
x=-4\left(x+2\right)\to x=-4x-8
Agrupamos los términos con x en el primer miembro.
x=-4x-8\to x+4x=-8
5x=-8
\therefore x=-\frac{8}{5}
Concluimos indicando como respuesta correcta la opción A.
Reactivo 7: Inecuaciones lineales
Encuentra el rango de valores para x , que satisface las siguientes desigualdades.
x-1<0 3\le x+5
- -2<x\le 1
- -1\le x<2
- -2<x\le -1
- -2\le x<1
Solución:
Calcular el conjunto de valores de x que satisface ambas desigualdades, implica calcular la solución independiente de cada una e interceptar ambos conjuntos en la recta real.
Inecuación 1.
x-1<0
x-1+1<1
x<1
{Sol}_{1}=x\in \left(-\infty ,1\right)
Inecuación 2.
3\le x+5
x+5\ge 3
x+5-5\ge 3-5
x\ge -2
{Sol}_{2}=x\in [-2,\infty )
Interceptamos ambas soluciones.
Sol={Sol}_{1}\cap {Sol}_{2}
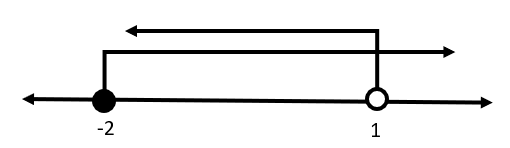
La intersección de los conjuntos es todos los números mejores o iguales a -2 y menores a 1.
-2\le x<1
Comparando con las opciones del problema, seleccionamos como respuesta correcta la opción D.
Reactivo 8: Sistema de ecuaciones lineal
¿Cuáles son las soluciones del siguiente sistema de ecuaciones?
y=x-3
4x+y=32
- x=5;y=12
- x=4;y=16
- x=8;y=5
- x=7;y=4
Solución:
Existen diferentes métodos para resolver sistemas de ecuaciones, todos llevan al mismo resultado, pero según el caso, simplifican la cantidad de operaciones que debemos realizar. En este caso, como en la primera ecuación se encuentra despejada la y , podemos simplemente sustituir en la segunda, calcular a x y por regresión a y .
Lo anterior descrito corresponde al método por sustitución por ello, ese será el método que emplearemos en esta ocasión.
Sustituyendo y en la segunda ecuación.
4x+x-3=32
Despejamos.
5x=35
\therefore x=7
Sustituimos el valor de x en la expresión de y .
y=x-3\to y=7-3=4
\therefore y=4
Concluimos entonces que las soluciones al sistema de ecuaciones son:
x=7;y=4
Esto se puede comprobar al graficar ambas ecuaciones.
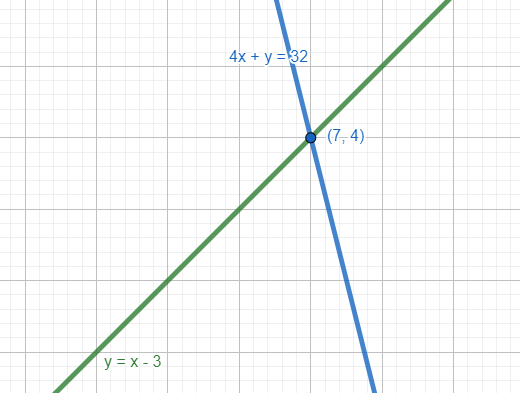
Concluimos seleccionando como respuesta correcta al inciso D.
Reactivo 9: Problemas con sistemas de ecuaciones
Cinco cuadernos y ocho lapiceros cuestan $115; tres cuadernos y cinco lapiceros cuestan $70. ¿Cuál es el precio de cada cuaderno?
- $15
- $10
- $13
- $12
Solución:
Debemos extraer las ecuaciones de las frases en el enunciado. Luego de tener el SEL, podremos aplicar cualquier método para encontrar el precio de cada cuaderno. A los lapiceros los llamaremos l y a los cuadernos c .
Cinco cuadernos y ocho lapiceros cuestan $115.
5c+8l=115
Tres cuadernos y cinco lapiceros cuestan $70.
3c+5l=70
El sistema de ecuaciones quedaría como:
\left\{\begin{array}{c}5c+8l=115 \\ 3c+5l=70\end{array}\right.
Ya que solo nos interesa el precio de cada cuaderno, aplicaremos el método por sustitución para obtener una expresión únicamente en función de c . Despejamos a l de la primera ecuación.
5c+8l=115\to 8l=115-5c
l=\frac{115-5c}{8}
Sustituimos en la segunda ecuación.
3c+5\left(\frac{115-5c}{8}\right)=70
Multiplicamos todo por 8.
24c+5\left(115-5c\right)=560
24c+575-25c=560
Despejamos a c .
24c-25c=560-575
-c=-15
\therefore c=15
Concluimos indicando que el precio de cada cuaderno es de $15. La respuesta correcta está en el inciso A.
Reactivo 10: Dominio de funciones
¿Cuál es el dominio de la siguiente función polinomial?
f\left(x\right)={x}^{3}+2{x}^{2}-3x+1
- \left[-\infty ,\infty \right]
- (-\infty ,1)
- \left(-\infty ,\infty \right)
- (-1,\infty )
Solución:
El dominio de una función real, es el conjunto de valores de x para los cuales, se obtiene una imagen de f al ser evaluados en su regla de correspondencia.
Las funciones polinómicas tienen como dominio a todos los números reales. No importa el número que elijas, siempre tendrá una imagen. Concluimos que: f\left(x\right)={x}^{3}+2{x}^{2}-3x+1 tiene como dominio a todos los números reales.
Dom\left(f\right)=x\in \left(-\infty ,\infty \right)
Seleccionamos como respuesta correcta la opción C.
Sigue practicando: 50 ejercicios de matemáticas del examen de la UNAM
Reactivo 11: Gráfica de una función
La gráfica de la función y=-x-1 corresponde a una recta que _________ de izquierda a derecha y que corta al eje de las ordenadas en ____________.
- asciende; \left(0,-1\right)
- desciende; \left(0,-1\right)
- desciende; \left(\mathrm{0,1}\right)
- asciende; \left(\mathrm{0,1}\right)
Solución:
Lo primero que podemos observar, es que la función corresponde a una recta en el plano real cuya pendiente es -1. Por tanto, desciende el valor de y a medida incrementamos las x o avanzamos de izquierda a derecha.
El corte con las ordenadas o eje de las y , se obtiene al hacer cero la x .
y=-0-1\to y=-1
La función lineal desciende y corta con las ordenadas en \left(0,-1\right) .
Escogemos como respuesta correcta al inciso B.
Reactivo 12: Funciones crecientes y decrecientes
¿Cuál de las siguientes funciones tiene un comportamiento creciente?
- f\left(x\right)=-3x
- f\left(x\right)={3}^{-x}
- f\left(x\right)=\frac{3}{x}
- f\left(x\right)={x}^{3}
Solución:
En términos generales, decimos que una función es creciente cuando y aumenta para aumentos de x y decreciente si y decrece para aumentos de x . Otra forma de decir que una función es creciente o decreciente, pasa por examinar su gráfica.
Si al desplazarnos de izquierda a derecha la gráfica va de arriba hacia abajo decrece, si va de menos a más crece. Basados en lo anterior y sin emplear la gráfica de las funciones, analizaremos cuál de ellas es creciente.
Primera función.
f\left(x\right)=-3x
Es una función lineal con pendiente negativa m=-3 por consiguiente, es decreciente para cualquier incremento de x .
Segunda función.
f\left(x\right)={3}^{-x}
Si aplicamos propiedades de la potenciación, la segunda función puede escribirse como:
f\left(x\right)={3}^{-x}=\frac{1}{{3}^{x}}
Corresponde a una función potencial que tiene valores más cercanos a cero a medida que x se acerca a +\infty , por tanto, es una función decreciente.
Tercera función.
f\left(x\right)=\frac{3}{x}
El dominio de esta función son todos los reales excepto en x=0 , punto en el que presenta una discontinuidad. Debemos analizar su crecimiento/decrecimiento para dos intervalos: \left(-\infty ,0\right) y \left(0,\infty \right) .
En el primer intervalo, la función tiene valores más negativos a medida que x se acerca a cero, punto en el que por la izquierda se va hacia -\infty . Para el segundo, en cero por la derecha la función decrece desde infinito positivo hasta hacerse cada vez más pequeña a medida que x incrementa.
Concluimos entonces que la función 3 es decreciente en sus dos intervalos de existencia.
Cuarta función.
f\left(x\right)={x}^{3}
La última función es de tercer grado e incrementa rápidamente su valor cuando nos movemos de izquierda a derecha. La cuarta función es la única de tipo creciente en los 4 incisos.
Seleccionamos como respuesta correcta la opción D.
Reactivo 13: Conversión entre ángulos
Convierte el valor de un ángulo que mide \frac{2}{4}\pi radianes a grados.
- 270°
- 90°
- 60°
- 240°
Solución:
Para pasar un ángulo que se encuentra en radianes a grados, empleamos la siguiente relación:
180°\to \pi rad
Hacemos una sencilla regla de tres.
\pi rad\to 180°
\frac{2}{4}\pi \to x
Entonces:
x=\frac{\frac{2}{4}\pi *180°}{\pi }=\frac{2}{4}*180°=90°
Concluimos que \frac{2}{4}\pi es igual a 90°.
Seleccionamos como respuesta correcta la opción B.
Reactivo 14: Razones trigonométricas
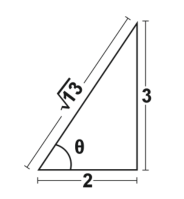
A partir de la siguiente imagen, determina la razón trigonométrica que corresponde a la secante del ángulo \theta .
- \frac{2}{\sqrt{13}}
- \frac{\sqrt{13}}{2}
- \frac{3}{\sqrt{13}}
- \frac{\sqrt{13}}{3}
Solución:
La secante es la relación trigonométrica inversa del coseno y representa el cociente entre la hipotenusa y el cateto adyacente a \theta .
sec\theta =\frac{H}{CA}
Basados en la imagen, sabemos que la hipotenusa vale \sqrt{13} unidades y el cateto adyacente a \theta 2 unidades. Sustituimos en la relación trigonométrica.
sec\theta =\frac{\sqrt{13}}{2}
Concluimos entonces que la respuesta correcta es el inciso B.
Reactivo 15: Dominio y rango de una función real
El dominio D y el rango R de la función f\left(x\right)=\frac{{e}^{x}}{-5} son
- D=\left(-\infty ,0\right);R=\left(-\infty ,\infty \right)
- D=\left(0,\infty \right);R=\left(-\infty ,\infty \right)
- D=\left(-\infty ,\infty \right);R=\left(0,\infty \right)
- D=\left(-\infty ,\infty \right);R=\left(-\infty ,0\right)
Solución:
El dominio de una función es el conjunto de valores de x que, sustituidos en su regla de correspondencia, dan como resultado una imagen para f . Por otro lado, el rango es el conjunto de valores que corresponden a las imágenes de la función.
El cálculo de ambos conjuntos se resume en aplicar restricciones para que los resultados existan y sean finitos. Para el dominio no existe ninguna restricción, ya que una función potencial puede recibir como valor de entrada cualquier número real, por ende:
D=\left(-\infty ,\infty \right)
El rango se calcula primero determinando la inversa de la función y luego aplicando las mismas restricciones a y .
Inversa de f .
y=\frac{{e}^{x}}{-5}\to {e}^{x}=-5y
\therefore x=ln \left(-5y\right)
La restricción para el argumento de una función logarítmica, es que sea mayor que cero.
-5y>0
\therefore y<0
El rango de f es el conjunto de valores de la imagen que son menores a cero.
R=\left(-\infty ,0\right)
Concluimos que:
D=\left(-\infty ,\infty \right); R=\left(-\infty ,0\right)
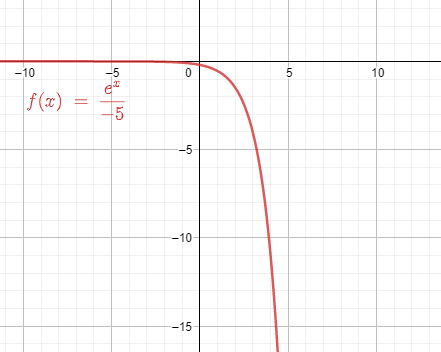
Comparando con las opciones, concluimos que la respuesta correcta es el inciso D.
Reactivo 16: Distancia entre dos puntos
Calcula la distancia entre los puntos P(-\mathrm{1,1}) y Q(1,-1) en el plano cartesiano.
- \sqrt{8}
- 2
- \sqrt{2}
- 4
Solución:
La distancia entre dos puntos en el plano cartesiano se calcula con la siguiente fórmula:
d\left(P,Q\right)=\sqrt{{\left({x}_{p}-{x}_{q}\right)}^{2}+{\left({y}_{p}-{y}_{q}\right)}^{2}}
Donde:
\left({x}_{p},{y}_{p}\right)=\left(-\mathrm{1,1}\right)
\left({x}_{q},{y}_{q}\right)=\left(1,-1\right)
Sustituimos.
d\left(P,Q\right)=\sqrt{{\left(-1-1\right)}^{2}+{\left(1+1\right)}^{2}}
Resolvemos.
d\left(P,Q\right)=\sqrt{{\left(-1-1\right)}^{2}+{\left(1+1\right)}^{2}}=\sqrt{{2}^{2}+{2}^{2}}=\sqrt{8}
d\left(P,Q\right)=\sqrt{8}=2.82842
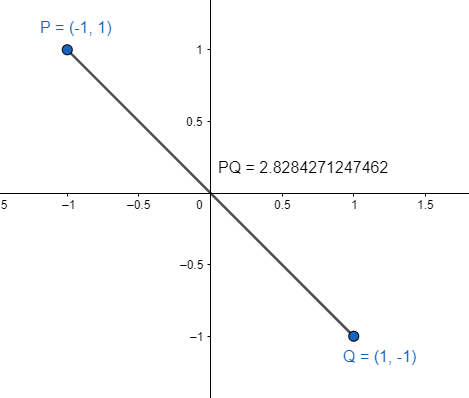
Concluimos indicando como respuesta correcta la opción A.
Reactivo 17: Distancia entre dos puntos
Calcula la distancia entre los puntos A(-7,-2) y B\left(\mathrm{2,7}\right) en el plano cartesiano.
- 162
- \sqrt{50}
- \sqrt{162}
- 50
Solución:
La distancia entre dos puntos en el plano real se calcula con la siguiente fórmula:
d\left(A,B\right)=\sqrt{{\left({x}_{a}-{x}_{b}\right)}^{2}+{\left({y}_{a}-{y}_{b}\right)}^{2}}
Donde:
\left({x}_{a},{y}_{a}\right)=\left(-7,-2\right)
\left({x}_{b},{y}_{b}\right)=\left(\mathrm{2,7}\right)
Sustituimos.
d\left(A,B\right)=\sqrt{{\left(-7-2\right)}^{2}+{\left(-2-7\right)}^{2}}
Resolvemos.
d\left(A,B\right)=\sqrt{{\left(-7-2\right)}^{2}+{\left(-2-7\right)}^{2}}=\sqrt{{9}^{2}+{9}^{2}}=\sqrt{162}
d\left(A,B\right)=\sqrt{162}=12.7279

Concluimos indicando como respuesta correcta la opción C.
Reactivo 18: Distancia entre dos puntos
Calcula la distancia entre los puntos A\left(\mathrm{1,1}\right) y B\left(-1,-1\right) en el plano cartesiano.
- 2\sqrt{2}
- 5\sqrt{2}
- 2
- 4
Solución:
La distancia entre dos puntos en el plano real se calcula con la siguiente fórmula:
d\left(A,B\right)=\sqrt{{\left({x}_{a}-{x}_{b}\right)}^{2}+{\left({y}_{a}-{y}_{b}\right)}^{2}}
Donde:
\left({x}_{a},{y}_{a}\right)=\left(\mathrm{1,1}\right)
\left({x}_{b},{y}_{b}\right)=\left(-1,-1\right)
Sustituimos.
d\left(A,B\right)=\sqrt{{\left(1+1\right)}^{2}+{\left(1+1\right)}^{2}}
Resolvemos.
d\left(A,B\right)=\sqrt{{\left(1+1\right)}^{2}+{\left(1+1\right)}^{2}}=\sqrt{{2}^{2}+{2}^{2}}=\sqrt{8}
d\left(A,B\right)=\sqrt{8}=2\sqrt{2}
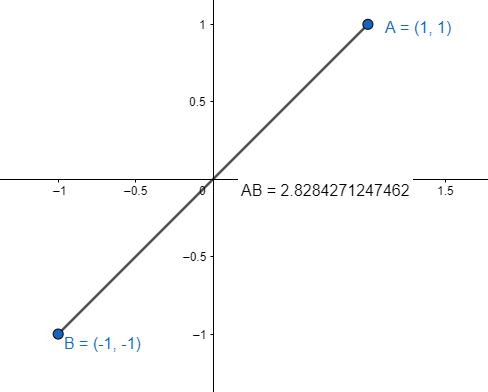
Concluimos indicando como respuesta correcta la opción A.
Reactivo 19: Ecuación de la circunferencia
¿Cuál de las siguientes ecuaciones corresponde a una circunferencia con centro en el origen y radio 2?
- {x}^{2}+{y}^{2}-4=0
- {x}^{2}-{y}^{2}-2=0
- {x}^{2}+{y}^{2}+2=0
- {x}^{2}-{y}^{2}-4=0
Solución:
Partimos de la ecuación ordinaria de la circunferencia con centro en \left(h,k\right) y radio r .
{\left(x-h\right)}^{2}+{\left(y-k\right)}^{2}={r}^{2}
En este caso, el centro tiene coordenadas \left(h,k\right)=\left(\mathrm{0,0}\right) y el radio una longitud r=2 unidades. Sustituimos los valores en la ecuación.
{\left(x-0\right)}^{2}+{\left(y-0\right)}^{2}={2}^{2}
{x}^{2}+{y}^{2}=4
Finalizamos pasando el 4 al primer miembro.
{x}^{2}+{y}^{2}-4=0
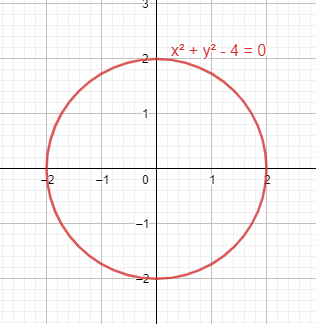
Seleccionamos como respuesta correcta la opción A.
Reactivo 20: Elementos de la circunferencia
¿Cuál es el centro y el radio de la siguiente circunferencia?
(x+3{)}^{2}+(y-2{)}^{2}=36
- C\left(\mathrm{3,2}\right);r=6
- C\left(\mathrm{3,2}\right);r=36
- C\left(-\mathrm{3,2}\right);r=6
- C\left(-\mathrm{3,2}\right);r=36
Solución:
Podemos extraer el radio y el centro a partir de la ecuación dada en forma ordinaria al observar ciertas partes de la expresión. Comencemos por el término independiente en el segundo miembro, que corresponde al cuadrado del radio.
36={r}^{2}
Despejamos.
r=\sqrt{36}=6
Por otra parte, las coordenadas del centro h y k se encuentran dentro de los paréntesis de x y y respectivamente.
h=-3;k=2
Concluimos entonces que:
C\left(-\mathrm{3,2}\right);r=6
Seleccionamos como respuesta correcta la opción C.
Reactivo 21: Vértice de la parábola
Calcula el vértice de la siguiente parábola.
(y-3{)}^{2}=12x-24
- V=\left(\mathrm{2,3}\right)
- V=\left(\mathrm{3,2}\right)
- V=\left(-3,-2\right)
- V=\left(-2,-3\right)
Solución:
La ecuación corresponde a una parábola con eje focal paralelo al eje horizontal de la forma:
{\left(y-k\right)}^{2}=4p\left(x-h\right)
Donde h,k son las coordenadas del vértice.
Por simple inspección, el valor de k se extrae del primer miembro: k=3 . En el caso de h , debemos extraer factor común 12 en el segundo miembro.
(y-3{)}^{2}=12x-24\to (y-3{)}^{2}=12\left(x-2\right)
\therefore h=2
Las coordenadas del vértice de la parábola son:
V\left(\mathrm{2,3}\right)
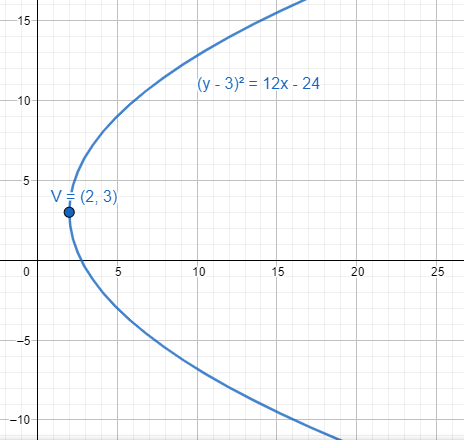
Comparando con las opciones del problema, escogemos como correcta la opción A.
Reactivo 22: La elipse
Determina las coordenadas de los focos de una elipse cuya ecuación es 9{x}^{2}+{y}^{2}=9
- {F}_{1}=\left(-\sqrt{8},0\right);{F}_{2}=\left(\sqrt{8},0\right)
- {F}_{1}=\left(-\sqrt{10},0\right);{F}_{2}=\left(\sqrt{10},0\right)
- {F}_{1}=\left(0,-\sqrt{8}\right);{F}_{2}=\left(0,\sqrt{8}\right)
- {F}_{1}=\left(0,-\sqrt{10}\right);{F}_{2}=\left(0,\sqrt{10}\right)
Solución:
Los focos de la elipse se encuentran a los lados del centro a una distancia c sobre el eje focal. Primero, debemos identificar si el eje focal es paralelo a las x o a las y .
9{x}^{2}+{y}^{2}=9
Dividimos todo por 9.
\frac{{x}^{2}}{1}+\frac{{y}^{2}}{9}=1
El parámetro de mayor magnitud se encuentra dividiendo a la y , por tanto, el eje focal es paralelo a las y , mientras que el centro posee coordenadas C\left(\mathrm{0,0}\right) . En base a esto, los focos de la elipse se sitúan de la siguiente manera:
{F}_{1}\left(0,-c\right);{F}_{2}\left(0,c\right)
Por otra parte, c puede calcularse a partir de la siguiente relación:
{a}^{2}={b}^{2}+{c}^{2}
Despejamos a c .
c=\sqrt{{a}^{2}-{b}^{2}}
Donde {a}^{2}=9 y {b}^{2}=1
c=\sqrt{9-1}=\sqrt{8}
Sustituimos los focos.
{F}_{1}\left(0,-\sqrt{8}\right);{F}_{2}\left(0,\sqrt{8}\right)
Finalmente, comparamos las opciones para seleccionar como correcta la C.
Reactivo 23: La hipérbola
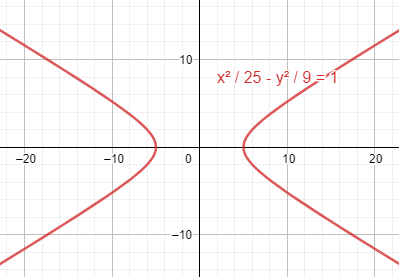
¿Cuál de las siguientes ecuaciones corresponde a la ecuación ordinaria de una hipérbola con centro en el origen y eje focal sobre el eje de las abscisas?
- \frac{{x}^{2}}{25}+\frac{{y}^{2}}{9}=1
- \frac{{x}^{2}}{25}-\frac{{y}^{2}}{9}=1
- \frac{{x}^{2}}{25}-\frac{y}{9}=1
- \frac{x}{25}-\frac{{y}^{2}}{9}=1
Solución:
Para las hipérbolas, el eje focal es paralelo a la variable que tenga el signo positivo. Ya que las abscisas corresponden al eje x , esta es la variable que debe quedar con signo positivo en la ecuación.
\frac{{\left(x-h\right)}^{2}}{{a}^{2}}-\frac{{\left(y-k\right)}^{2}}{{b}^{2}}=1
Por otra parte, las coordenadas del centro \left(h,k\right) son \left(\mathrm{0,0}\right) .
\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1
Comparando esta expresión base con las ecuaciones de cada inciso, el B tiene la respuesta correcta.
\frac{{x}^{2}}{25}-\frac{{y}^{2}}{9}=1
Reactivo 24: Ecuación general de segundo grado
¿Cuál de las siguientes representa la ecuación general de segundo grado con dos variables?
- A{x}^{2}+B{y}^{2}+C{z}^{2}+Dx{y}^{2}+2Exy=0
- A{x}^{2}+B{y}^{2}=0
- A{x}^{2}+Bx+C=0
- A{x}^{2}+Bxy+C{y}^{2}+Dx+Ey+F=0
Solución:
La ecuación general de segundo grado permite describir a todas las cónicas a partir del valor que tome cada parámetro, siempre que A , B o C sea diferente de cero. La ecuación general de segundo grado representa la expresión:
A{x}^{2}+Bxy+C{y}^{2}+Dx+Ey+F=0
Y se considera la definición geométrica que incluye a todas las cónicas y dos casos excepcionales: un punto o dos rectas.
En base al análisis anterior, la respuesta correcta se encuentra en el inciso D.

