Quinta parte, y final del examen simulacro de pensamiento matemático, vamos a responder los reactivos del 41 al 50, siendo estos los últimos 10 del simulacro Exani II.

¿Qué sigue? Una vez que termines el examen mi recomendación es que estudies los temas que más se te dificultaron e intentes resolverlo de nuevo cuando te tengas más conocimiento en la materia (que espero sea dentro de un par de días).
Todas las partes del Simulacro:
Recuerda que este simulacro estará disponible siempre que quieras practicar, asi como muchos otros contenidos de estudio gratuitos en la sección de materiales en el menú del sitio.
Reactivo 41
Se tiene un gráfico de barra que representa la cantidad de clientes en un restaurante para cada día de la semana.
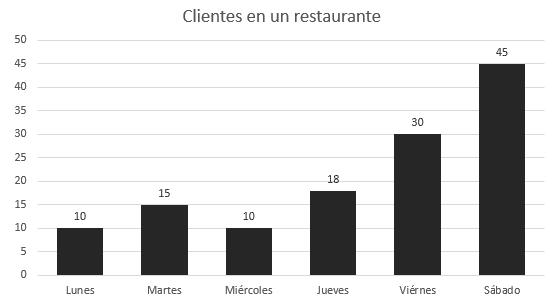
¿Cuál es la desviación típica del conjunto de datos?
- 21.33
- 157.21
- 12.538
Solución:
La desviación típica o estándar, es un parámetro estadístico que nos permite cuantificar el nivel de dispersión de los datos respecto de la media. La desviación estándar se calcula como:
\sigma =\sqrt{\frac{\sum {\left({x}_{i}-\stackrel{-}{x}\right)}^{2}}{N}}
Donde:
- {x}_{i} es el i-ésimo dato del conjunto.
- \stackrel{-}{x} es la media de los datos.
- N el total de datos.
Iniciamos por calcular la media aritmética.
\stackrel{-}{x}=\frac{10+15+10+18+30+45}{6}=21.33
Ahora, calculamos la diferencia de los datos respecto a la media en una tabla.
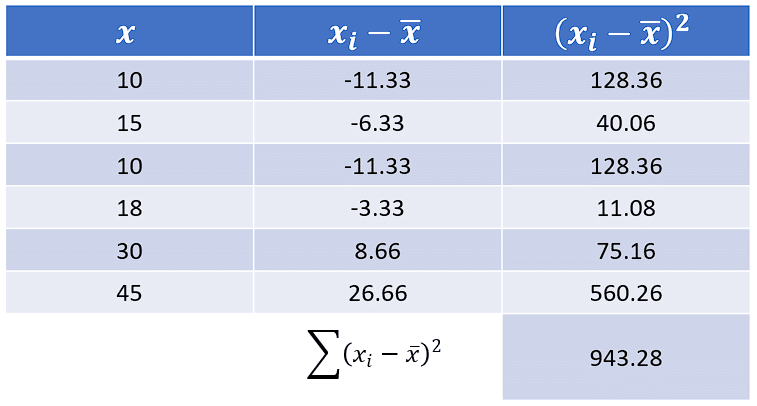
Finalmente, sustituimos los valores en la ecuación de la desviación típica.
\sigma =\sqrt{\frac{943.28}{6}}=12.538
Concluimos que la respuesta correcta es el inciso c).
Pregunta 42
Un estudio de mercado, arroja que la demanda de cierto producto en los últimos 24 meses tiene una pendiente de +500.
¿Cuál de las siguientes aseveraciones es correcta?
- La demanda decrece linealmente
- La demanda tiene una media mensual de 500 unidades
- La demanda aumenta linealmente
Solución:
Cuando hablamos de una pendiente, nos referimos a variaciones constantes de una variable dependiente, normalmente y , respecto de otra variable independiente, que suele denotarse como x .
Ahora, estas variaciones lineales pueden ser de incrementos o decrementos. Sabremos que se trata de la primera si la pendiente es positiva, o de la segunda si es negativa. Debido a que la pendiente es positiva, decimos que la demanda incrementa en 500 unidades a medida que pasan los meses.
Concluimos que la respuesta correcta es el inciso c).
Pregunta 43
Se realizó un estudio acerca del peso en recién nacidos durante una semana en el centro de maternidad de un hospital. La siguiente gráfica resume los datos recolectados.
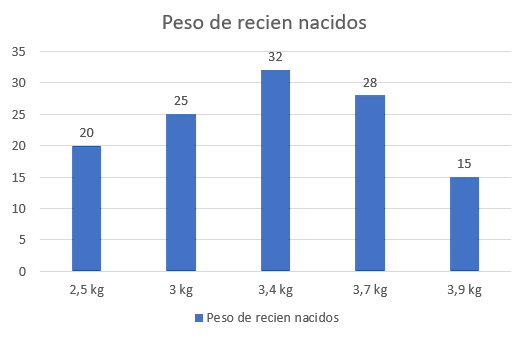
¿Cuál es el peso más cercano a la media?
- 3.3 \mathrm{k}\mathrm{g}
- 3.4 \mathrm{k}\mathrm{g}
- 3 \mathrm{k}\mathrm{g}
Solución:
Iniciamos calculando la media aritmética del peso de los infantes. En este caso, empleamos la ecuación de la media que depende de la frecuencia absoluta de los datos.
\stackrel{-}{x}=\frac{\sum {f}_{i}{x}_{i}}{N}
Sustituyendo los valores en la ecuación, a partir de los datos suministrados por el gráfico nos queda:
\stackrel{-}{x}=\frac{\left(2.5\right)\left(20\right)+\left(3\right)\left(25\right)+\left(3.4\right)\left(32\right)+\left(3.7\right)\left(28\right)+\left(3.9\right)\left(15\right)}{20+25+32+28+15}=3.299\approx 3.3 \mathrm{k}\mathrm{g}
El promedio del peso es de 3.3 kilogramos. Teniendo en cuenta ahora los valores de la tabla, el más cercano a la media es 3.4 kilogramos. La respuesta correcta al ejercicio es el inciso b).
Pregunta 44
Encuentre la ecuación de la parábola y={x}^{2}+1 , luego de trasladar su vértice al punto {V}^{\text{'}}\left(1, -1\right) .
- {\left(x+1\right)}^{2}=y+1
- {\left(x-1\right)}^{2}=y+1
- {\left(x-1\right)}^{2}=y-1
Solución:
Examinando la ecuación de la parábola, se trata de una que abre de forma vertical. Comparándola con su forma general, podemos obtener las coordenadas del centro antes de trasladarlo.
{\left(x-h\right)}^{2}=4p\left(y-k\right)
Obtenemos que:
y-1={x}^{2}\to {\left(x-0\right)}^{2}=y-1
V\left(0, 1\right)
La gráfica de esta parábola sería:
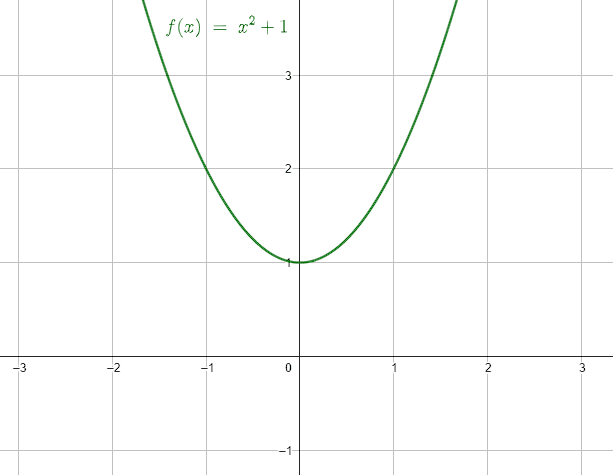
Ahora, cambiamos las coordenadas del vértice: {V}^{\text{'}}\left(1, -1\right) .
{\left(x-1\right)}^{2}=y+1
Gráficamente:
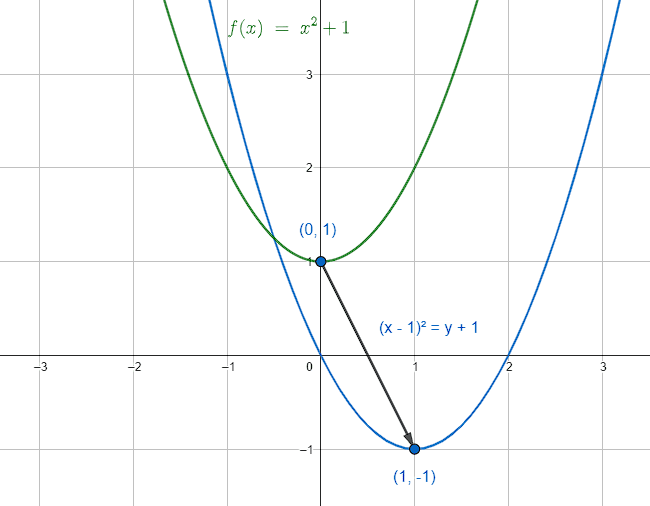
Concluimos que la respuesta correcta es el inciso b).
Pregunta 45
Sean los puntos A\left(1, 1\right) y B\left(2x, x\right) , ¿cuánto debe valer x>0 para que la distancia entre los puntos sea igual a 4 ?
- B\left(4.754, 2.377\right)
- B\left(2.377, 2.377\right)
- B\left(-4.754, 2.377\right)
Solución:
Para encontrar el valor de x mayor que cero que satisfaga la condición, empleamos la ecuación de distancia entre dos puntos.
{4}^{2}={\left(1-2x\right)}^{2}+{\left(1-x\right)}^{2}
Desarrollamos las potencias.
16=1-4x+4{x}^{2}+1-2x+{x}^{2}\to 16=2-6x+5{x}^{2}
Simplificamos y agrupamos.
5{x}^{2}-6x-14=0
Empleamos la fórmula de segundo grado.
x=\frac{-\left(-6\right)\pm \sqrt{{\left(-6\right)}^{2}-4\left(5\right)\left(-14\right)}}{2\left(5\right)}=\frac{6\pm \sqrt{316}}{10}
De las dos posibles soluciones, la única que arrojará un valor positivo es:
x=\frac{6+\sqrt{316}}{10}\approx 2.377
Sustituimos este valor aproximado en la ecuación de distancia para comprobar.
{4}^{2}={\left(1-2\left(2.377\right)\right)}^{2}+{\left(1-\left(2.377\right)\right)}^{2}
16=15.988\approx 16
Finalmente:
B\left(4.754, 2.377\right)
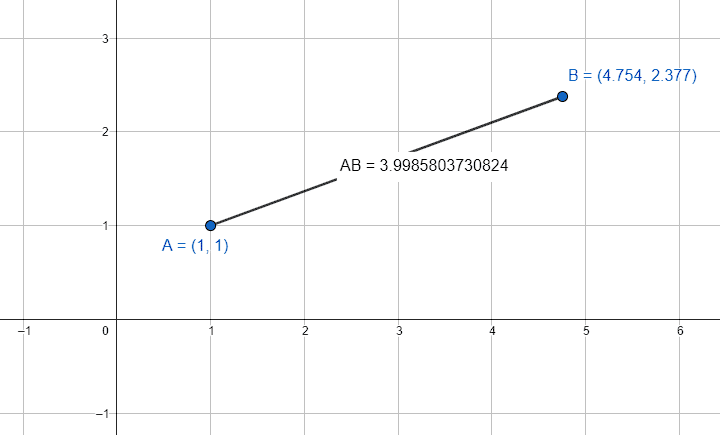
Concluimos indicando como respuesta correcta al inciso a).
Reactivo 46
El profesor de historia de Juan solicita a su clase crear grupos de 3 integrantes. Si la clase está compuesta por 27 estudiantes, ¿de cuántas formas podría Juan hacer grupo con sus compañeros?
- 325
- 305
- 625
Solución:
Iniciemos identificando que al ser de 3 integrantes los grupos, Juan ya forma parte de esos 3 por tanto, quedan 2 espacios disponibles en su grupo. En este caso no importa el orden que tengan Juan y sus compañeros en el grupo, ya que no se ha establecido una jerarquía en los mismos.

Esto nos deja con 26 estudiantes para ser agrupados de 2 en 2. Debido a que no importa el orden, la técnica de conteo a emplear es: combinaciones.
{C}_{n}^{m}=\frac{m!}{\left(m-n\right)!n!}
Tenemos que: m=35 y n=2 . Sustituimos:
{C}_{2}^{26}=\frac{26!}{\left(26-2\right)!2!}=325
Juan puede combinar su grupo con el resto de compañeros de 325 formas distintas.
Concluimos que la respuesta correcta es el inciso a).
Pregunta 47
Una empresa ha entrevistado a un grupo de recién egresados y ha seleccionado a Gabriela y Estefanía para realizar la selección final. En los requisitos, se toma en cuenta: zona de residencia, nota del examen técnico, promedio universitario y materias electivas cursadas relacionadas con el cargo. Será seleccionada la aspirante que más requisitos cumpla entre las dos.
La siguiente tabla resume las aptitudes de ambas aspirantes.

¿Cuál debe seleccionar la empresa?
- Gabriela
- Estefanía
- Ninguna de las dos aspirantes
Solución:
En este caso, solo debemos determinar cuál de las dos aspirantes sobresale en la mayor cantidad de aptitudes solicitadas por la empresa. Con sobresalir en al menos 3, dicha candidata será seleccionada.
En la zona de residencia, puntaje en el examen técnico y promedio universitario, destaca Gabriela. Por tanto, es ella quien se queda con el puesto. La respuesta correcta es el inciso a).
Pregunta 48
Una empresa desarrolladora de videojuegos ha tenido un incremento en ventas durante el último mes del 45%. A los empleados se les paga de la siguiente forma: 12,550$ de sueldo base y un 0.25% de dividendos por concepto de ventas en la empresa.
Si el flujo de caja promedio es de 2,500,000$ al mes, ¿cuánto ganará un empleado al final del mes actual?
- 21563\mathrm{\$}
- 9063\mathrm{\$}
- 3437\$
Solución:
Para calcular el salario del empleado, debemos sumarle a su ingreso mensual el 0.25% por concepto de dividendos.
\mathrm{S}=12500+{\mathrm{D}}_{0.25\mathrm{\%}}
El enunciado nos dice que el flujo de caja promedio es de 2,500,000$/mes, incrementando el 45% nos queda:
\mathrm{I}\mathrm{n}\mathrm{g}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{o}\mathrm{s}=1.45\cdot 2500000=3625000\mathrm{\$}
El 0.25% de esta cifra es:
{\mathrm{D}}_{0.25\mathrm{\%}}=0.0025\cdot 3625000=9063\mathrm{\$}
Finalmente:
\mathrm{S}=12500+9063=21563\mathrm{\$}
Concluimos que la respuesta correcta es el inciso a).
Pregunta 49
El parámetro estadístico que permite dividir en 5 partes iguales un conjunto de datos se denomina:
- Moda
- Mediana
- Cuartil
Solución:
Los cuartiles, son 4 valores que pertenecen al conjunto de datos y que permiten dividirlo en 5 subconjuntos con la misma cantidad de elementos. La respuesta correcta es el inciso c).
Pregunta 50
¿Cuál de los siguientes términos es un parámetro estadístico de dispersión?
- Desviación típica
- Media
- Percentil 75
Solución:
Los parámetros de dispersión, son aquellos que cuantifican la separación entre los datos respecto de otro parámetro estadístico, por ejemplo, de la media o entre ellos mismos. Los parámetros de dispersión más conocidos son: la varianza, la desviación típica y el rango.
Teniendo en cuenta lo anterior, la respuesta correcta es el inciso a).

