Examen Simulador de Cálculo UNAM | Áreas 1 y 2

¡Bienvenido aspirante! En este post vamos a resolver los primeros 10 reactivos del Simulador de Cálculo para el examen de admisión a la UNAM, para las áreas 1 y 2.

La materia de cálculo únicamente viene en el examen de admisión de las carreras que pertenecen a las carreras de Ciencias Físico-Matemáticas y de las Ingenierías y Ciencias Biológicas, Químicas y de la Salud.

A continuación tienes un resumen de los puntos más resaltantes del examen de ingreso a la UNAM.

• Desarrollo: UNAM
• Materia: Matemáticas – Cálculo
• Reactivos: 120
• Tipo: Opción múltiple
• Duración: 3 horas
• Modalidades: Presencial

Recuerda resolver los reactivos por tu cuenta, tu calificación es proporcional esfuerzo que dediques durante la preparación.

Estructura del examen UNAM

La prueba de ingreso tiene una extensión total de 120 problemas, pero la distribución de reactivos por materia varía en función al área que pertenece tu carrera. La siguiente tabla resume la estructura del examen UNAM para las 4 áreas.

Temas	Área 1	Área 2	Área 3	Área 4
Español	18	18	18	18
Matemáticas	26	24	24	22
Física	16	12	10	10
Química	10	13	10	10
Biología	10	13	10	10
Historia universal	10	10	14	10
Historia de México	10	10	14	10
Literatura	10	10	10	10
Geografía	10	10	10	10
Filosofía	NA	NA	NA	10
Total	120	120	120	120

¿Quieres conocer todos los detalles del examen a la UNAM?

Además del examen de ingreso, algunas facultades en la UNAM aplican pruebas adicionales a sus aspirantes en lo que se conoce como ingreso indirecto.

¿Cómo estudiar cálculo?

Cálculo representa un salto enorme comparado con el álgebra y la geometría. Es importante comprender los conceptos básicos para tener plena consciencia a la hora de integrar y derivar. No seguir este consejo puede afectar tus aciertos del examen, disminuyendo la nota final.

A continuación, te dejo algunos consejos que puedes poner en práctica para mejorar tu rendimiento a la hora de estudiar cálculo.

Temario cálculo UNAM

En la siguiente lista tienes el temario de cálculo para el área 1 y 2 de la UNAM. Puedes acceder a mayor información sobre el examen y la convocatoria UNAM en el resto de artículos que hemos preparado para ti.

Reactivo 1

A partir del gráfico que se muestra a continuación, determine qué pasa con la función cuando x tiende a +\infty  .

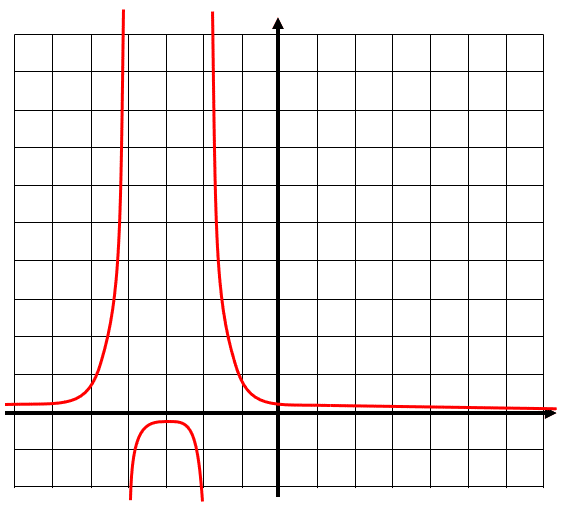
1. Tiende a +\infty
2. Tiende a cero
3. La función se indetermina
4. Tiende a 1

Solución:

Para responder al enunciado, debemos recordar un concepto fundamental en el cálculo diferencial: el límite de una función.

Cuando decimos que la variable x tiende a cierto valor a , significa que x se acerca a ese valor, pero nunca es igual a él. La notación para representar esto es: x\to a y se lee como: “equis que tiende a valer a”.

El objetivo es ver qué pasa con el valor de la función a medida que nos acercamos al valor a , en este caso: a=\infty  , para emitir una conclusión.

Si nos referimos a la gráfica, el trazo de color rojo corresponde a la función. Si nos movemos con la x hacia el +\infty  , vemos que la función se hace cada vez más cercana a cero. Esto se puede escribir como:

x\to +\infty  \leftrightarrow y\to 0

“Cuando equis tiende a más infinito, la función tiende a cero”

Teniendo en cuenta nuestro análisis, concluimos que la respuesta correcta es el inciso b).

Reactivo 2

Calcule el valor del siguiente límite.

\underset{x\to -1}{\mathrm{lim}}\frac{x+1}{{x}^{2}-4x+3}

1. L=0
2. L=-1
3. L=\frac{1}{2}
4. L=\infty

Solución:

El primer paso para resolver el límite de una función, es evaluarla en el punto de tendencia. En este caso corresponde a -1.

\underset{x\to -1}{\mathrm{lim}}\frac{x+1}{{x}^{2}-4x+3}=\frac{-1+1}{{\left(-1\right)}^{2}-4\left(-1\right)+3}=\frac{0}{1+4+3}=0

Debido a que no se presenta ninguna indeterminación, concluimos que el límite de la función cuando x\to -1 es cero.

La respuesta correcta es el inciso a).

Reactivo 3

Obtenga el valor del siguiente límite.

\underset{x\to 3}{\mathrm{lim}}\frac{x\sqrt{x}-3\sqrt{3}}{\sqrt{x}-\sqrt{3}}

1. -9
2. 9
3. 0
4. 4

Solución:

Comenzamos por evaluar el límite para verificar si se presenta o no una indeterminación.

\underset{x\to 3}{\mathrm{lim}}\frac{x\sqrt{x}-3\sqrt{3}}{\sqrt{x}-\sqrt{3}}=\frac{3\sqrt{3}-3\sqrt{3}}{\sqrt{3}-\sqrt{3}}=\frac{0}{0}

Una indeterminación cero sobre cero.

En este caso, no podemos extraer ningún término o coeficiente como factor común. Nos queda multiplicar y dividir por el conjugado del denominador.

\underset{x\to 3}{\mathrm{lim}}\frac{x\sqrt{x}-3\sqrt{3}}{\sqrt{x}-\sqrt{3}}\cdot \frac{\sqrt{x}+\sqrt{3}}{\sqrt{x}+\sqrt{3}}=\underset{x\to 3}{\mathrm{lim}}\frac{\left(x\sqrt{x}-3\sqrt{3}\right)\left(\sqrt{x}+\sqrt{3}\right)}{\left(\sqrt{x}-\sqrt{3}\right)\left(\sqrt{x}+\sqrt{3}\right)}

Desarrollamos y simplificamos:

\underset{x\to 3}{\mathrm{lim}}\frac{\left(x\sqrt{x}-3\sqrt{3}\right)\left(\sqrt{x}+\sqrt{3}\right)}{\left(\sqrt{x}-\sqrt{3}\right)\left(\sqrt{x}+\sqrt{3}\right)}=\underset{x\to 3}{\mathrm{l}\mathrm{i}\mathrm{m}}\frac{\left(x\sqrt{x}-3\sqrt{3}\right)\left(\sqrt{x}+\sqrt{3}\right)}{x-3}

No vamos a desarrollar el numerador, porque ahora debemos multiplicar y dividir por su conjugado.

\underset{x\to 3}{\mathrm{l}\mathrm{i}\mathrm{m}}\frac{\left(x\sqrt{x}-3\sqrt{3}\right)\left(\sqrt{x}+\sqrt{3}\right)}{x-3}=\underset{x\to 3}{\mathrm{l}\mathrm{i}\mathrm{m}}\frac{\left(x\sqrt{x}-3\sqrt{3}\right)\left(\sqrt{x}+\sqrt{3}\right)}{x-3}\cdot \frac{x\sqrt{x}+3\sqrt{3}}{x\sqrt{x}+3\sqrt{3}}

\underset{x\to 3}{\mathrm{l}\mathrm{i}\mathrm{m}}\frac{\left({x}^{3}-27\right)\left(\sqrt{x}+\sqrt{3}\right)}{\left(x-3\right)\left(x\sqrt{x}+3\sqrt{3}\right)}

Si desarrollamos los productos tal como se encuentran ahora, obtendremos términos con exponentes fraccionarios que no nos llevarán a nada. Pongamos atención en el factor {x}^{3}-27 que puede escribirse como {x}^{3}-{3}^{3} .

Es una diferencia de cubos que es igual a:

{x}^{3}-{3}^{3}=\left(x-3\right)\left({x}^{2}+3x+9\right)

Sustituimos y simplificamos:

\underset{x\to 3}{\mathrm{l}\mathrm{i}\mathrm{m}}\frac{\left(x-3\right)\left({x}^{2}+3x+9\right)\left(\sqrt{x}+\sqrt{3}\right)}{\left(x-3\right)\left(x\sqrt{x}+3\sqrt{3}\right)}=\underset{x\to 3}{\mathrm{l}\mathrm{i}\mathrm{m}}\frac{\left({x}^{2}+3x+9\right)\left(\sqrt{x}+\sqrt{3}\right)}{x\sqrt{x}+3\sqrt{3}}

Intentamos evaluar el límite.

\underset{x\to 3}{\mathrm{l}\mathrm{i}\mathrm{m}}\frac{\left({x}^{2}+3x+9\right)\left(\sqrt{x}+\sqrt{3}\right)}{x\sqrt{x}+3\sqrt{3}}=\frac{\left({3}^{2}+3\left(3\right)+9\right)\left(\sqrt{3}+\sqrt{3}\right)}{3\sqrt{3}+3\sqrt{3}}=\frac{\left(27\right)\left(2\sqrt{3}\right)}{6\sqrt{3}}

\frac{\left(27\right)\left(2\sqrt{3}\right)}{6\sqrt{3}}=\frac{\left(27\right)\left(2\right)}{6}=9

Finalmente decimos que:

\underset{x\to 3}{\mathrm{lim}}\frac{x\sqrt{x}-3\sqrt{3}}{\sqrt{x}-\sqrt{3}}=9

La respuesta correcta es el inciso b).

Reactivo 4

Determine el valor del siguiente límite al infinito.

\underset{x\to \infty }{\mathrm{lim}}\frac{{x}^{3}+64}{\sqrt{{x}^{2}-4}}

1. \infty
2. 0
3. -\infty
4. \nexists

Solución:

Comenzamos evaluando el límite para verificar el tipo de indeterminación.

\underset{x\to \infty }{\mathrm{lim}}\frac{{x}^{3}+64}{\sqrt{{x}^{2}-4}}=\frac{{\infty }^{3}+64}{\sqrt{{\infty }^{2}-4}}=\frac{\infty }{\infty }

Debemos romper la indeterminación cero sobre cero.

La regla general para atacar límites al infinito de funciones racionales con polinomios en el numerador y denominador, es dividir por x elevada al mayor exponente al numerador y denominador. En este caso, {x}^{3} .

\underset{x\to \infty }{\mathrm{lim}}\frac{\frac{{x}^{3}+64}{{x}^{3}}}{\frac{\sqrt{{x}^{2}-4}}{{x}^{3}}}=\underset{x\to \infty }{\mathrm{lim}}\frac{1+\frac{64}{{x}^{3}}}{\sqrt{\frac{{x}^{2}-4}{{x}^{3}}}}=\underset{x\to \infty }{\mathrm{lim}}\frac{1+\frac{64}{{x}^{3}}}{\sqrt{\frac{{x}^{2}}{{x}^{3}}-\frac{4}{{x}^{3}}}}=\underset{x\to \infty }{\mathrm{lim}}\frac{1+\frac{64}{{x}^{3}}}{\sqrt{\frac{1}{x}-\frac{4}{{x}^{3}}}}

Evaluamos el límite.

\underset{x\to \infty }{\mathrm{lim}}\frac{1+\frac{64}{{x}^{3}}}{\sqrt{\frac{1}{x}-\frac{4}{{x}^{3}}}}=\frac{1+\frac{64}{{\infty }^{3}}}{\sqrt{\frac{1}{\infty }-\frac{4}{{\infty }^{3}}}}=\frac{1+0}{\sqrt{0-0}}=\frac{1+0}{0}=\infty 

Infinito es un resultado válido. Significa que: cuando x tiende a infinito, el valor de la función también tiende a infinito.

La respuesta correcta es el inciso a).

Reactivo 5

Determine si la función g\left(x\right)=\frac{2-\sqrt{x}}{4-x} es discontinua en {x}_{0}=4 , de ser así, indique el tipo de discontinuidad.

1. Continua
2. Discontinuidad evitable
3. Discontinuidad de salto finito
4. Discontinuidad de salto infinito

Solución:

A partir del estudio del límite de una función en un punto {x}_{0} , se puede determinar si es o no continua en dicho valor. A continuación, las condiciones de continuidad:

1. El límite de f cuando x\to {x}_{o} debe existir
2. {x}_{o} debe pertenecer al dominio de f
3. El valor del límite y debe ser igual a la función evaluada en {x}_{o} : \underset{x\to {x}_{o}}{\mathrm{lim}}f\left(x\right)=f\left({x}_{o}\right)

Cuando una o todas condiciones no se cumplen, se presenta una discontinuidad.

Comencemos estudiando la existencia de la función en {x}_{0}=4 . Si examinamos el denominador de la función, vemos que al sustituir x=4 la función se indetermina, por tanto:

f\left(x=4\right)=\nexists 

La función es discontinua en x=4 , ahora solo nos queda determinar el tipo estudiando el límite cuando x\to 4 .

\underset{x\to 4}{\mathrm{lim}}\frac{2-\sqrt{x}}{4-x}

Evaluamos:

\underset{x\to 4}{\mathrm{lim}}\frac{2-\sqrt{x}}{4-x}=\frac{2-\sqrt{4}}{4-4}=\frac{0}{0}

Multiplicamos y dividimos por el conjugado del numerador.

\underset{x\to 4}{\mathrm{lim}}\frac{2-\sqrt{x}}{4-x}\cdot \frac{2+\sqrt{x}}{2+\sqrt{x}}=\underset{x\to 4}{\mathrm{lim}}\frac{4-x}{\left(4-x\right)\left(2+\sqrt{x}\right)}=\underset{x\to 4}{\mathrm{lim}}\frac{1}{2+\sqrt{x}}

Evaluamos.

\underset{x\to 4}{\mathrm{lim}}\frac{1}{2+\sqrt{x}}=\frac{1}{2+\sqrt{4}}=\frac{1}{4}

El límite de g\left(x\right) existe y vale \frac{1}{4} . Concluimos que la función tiene una discontinuidad evitable en x=4 .

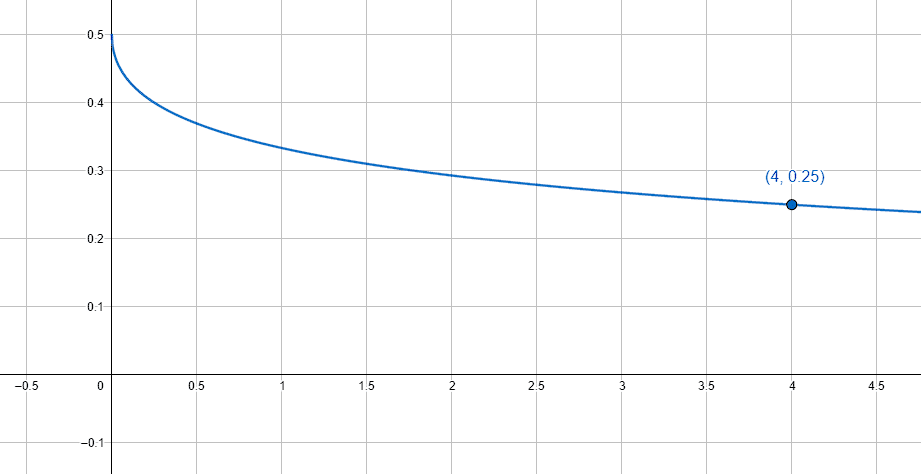
Indicamos como respuesta correcta al inciso b).

Reactivo 6

Identifique cuál de los siguientes límites permite obtener la derivada por definición de la función:

f\left(x\right)={x}^{2}+1

1. \underset{h\to 0}{\mathrm{lim}}\frac{{\left(x-h\right)}^{2}+1-{x}^{2}-1}{h}
2. \underset{h\to 0}{\mathrm{lim}}\frac{{\left(x+h\right)}^{2}+1-{x}^{2}-1}{h}
3. \underset{h\to 0}{\mathrm{lim}}\frac{{\left(x+h\right)}^{2}+1+{x}^{2}+1}{h}
4. \underset{h\to 0}{\mathrm{lim}}\frac{{\left(x+h\right)}^{2}+1-{x}^{2}-1}{h-x}

Solución:

Comencemos recordando la fórmula de la derivada por definición:

\underset{h\to 0}{\mathrm{lim}}\frac{f\left(x+h\right)-f\left(x\right)}{h}

Debemos sustituir las funciones correspondientes para f\left(x+h\right) y f\left(x\right) . Para la primera, sustituimos a la x por x+h , de tal forma que:

f\left(x+h\right)={\left(x+h\right)}^{2}+1

La segunda es simplemente la función en sí.

f\left(x\right)={x}^{2}+1

Sustituimos en el límite.

\underset{h\to 0}{\mathrm{lim}}\frac{{\left(x+h\right)}^{2}+1-{x}^{2}-1}{h}

Comparando con los incisos, concluimos que la respuesta correcta es b).

Reactivo 7

Calcule la derivada por fórmula de la función f\left(x\right)=\frac{1}{{x}^{2}+1} .

1. -\frac{2x}{{\left({x}^{2}+1\right)}^{2}}
2. \frac{2x}{{\left({x}^{2}+1\right)}^{2}}
3. -\frac{x}{{\left({x}^{2}+1\right)}^{2}}
4. -\frac{2x}{{\left({x}^{2}+1\right)}^{3}}

Solución:

Para resolver derivadas con fórmulas, debemos identificar a la función principal. En este caso es la función racional. Comenzamos aplicando la fórmula de la derivada de un cociente.

{f}^{\text{'}}\left(x\right)=\frac{{\left(1\right)}^{\text{'}}\left({x}^{2}+1\right)-{\left({x}^{2}+1\right)}^{\text{'}}\left(1\right)}{{\left({x}^{2}+1\right)}^{2}}

Resolvemos las derivadas indicadas. La derivada de 1 es cero y para {x}^{2}+1 aplicamos la derivada de una suma.

\frac{{\left(1\right)}^{\text{'}}\left({x}^{2}+1\right)-{\left({x}^{2}+1\right)}^{\text{'}}\left(1\right)}{{\left({x}^{2}+1\right)}^{2}}=\frac{0-2x}{{\left({x}^{2}+1\right)}^{2}}=-\frac{2x}{{\left({x}^{2}+1\right)}^{2}}

Esta es la forma más simplificada de la derivada de f\left(x\right) .

{f}^{\text{'}}\left(x\right)=-\frac{2x}{{\left({x}^{2}+1\right)}^{2}}

Indicamos como respuesta correcta al inciso a).

Reactivo 8

¿Cuál es la derivada de la función g\left(x\right)=\mathrm{ln}\left(x+1\right)-\mathrm{ln}\left(x\right) ?

1. \frac{1}{{x}^{2}\left(x+1\right)}
2. -\frac{1}{{x}^{2}\left(x+1\right)}
3. \frac{1}{x\left(x+1\right)}
4. -\frac{1}{x\left(x+1\right)}

Solución:

Antes de aplicar las respectivas fórmulas de derivadas, examinemos la expresión para intentar simplificar. Ya que tenemos dos logaritmos de la misma base restándole, podríamos aplicar la propiedad del logaritmo de un cociente.

g\left(x\right)=\mathrm{ln}\left(\frac{x+1}{x}\right)=\mathrm{ln}\left(1+\frac{1}{x}\right)

Empleamos la fórmula de la derivada de un logaritmo.

{g}^{\text{'}}\left(x\right)={\left[\mathrm{ln}\left(\frac{x+1}{x}\right)\right]}^{\text{'}}=\frac{{\left(1+\frac{1}{x}\right)}^{\text{'}}}{1+\frac{1}{x}}

Resolvemos la derivada indicada.

{g}^{\text{'}}\left(x\right)=\frac{-\frac{1}{{x}^{2}}}{1+\frac{1}{x}}

Simplificamos.

{g}^{\text{'}}\left(x\right)=\frac{-\frac{1}{{x}^{2}}}{\frac{x+1}{x}}=-\frac{x}{{x}^{2}\left(x+1\right)}=-\frac{1}{x\left(x+1\right)}

\therefore {g}^{\text{'}}\left(x\right)=-\frac{1}{x\left(x+1\right)}

Concluimos que la respuesta correcta es el inciso d).

Reactivo 9

¿Cuál es la derivada de la función trigonométrica h\left(x\right)={\mathrm{cos}}^{2}x ?

1. \mathrm{cos}x\mathrm{sin}x
2. -\mathrm{cos}x\mathrm{sin}x
3. -2\mathrm{cos}x\mathrm{sin}x
4. 2\mathrm{cos}x\mathrm{sin}x

Solución:

En este caso tenemos a una función coseno elevada al cuadrado. Según la regla de la cadena, debemos comenzar aplicando la fórmula para la derivada de una potencia.

{h}^{\text{'}}\left(x\right)={\left[{\mathrm{cos}}^{2}x\right]}^{\text{'}}=2\cdot \mathrm{cos}x\cdot {\left(\mathrm{cos}x\right)}^{\text{'}}

Ahora, resolvemos la derivada indicada aplicando la fórmula de la derivada del coseno.

{h}^{\text{'}}\left(x\right)=2\mathrm{cos}x\left(-\mathrm{sin}x\right)=-2\mathrm{cos}x\mathrm{sin}x

Comparando con las opciones, concluimos que la respuesta correcta es c).

Reactivo 10

Aplicando la regla de la cadena, determine la derivada de la función f\left(x\right)=\mathrm{ln}\sqrt{{x}^{2}+1} .

 

Solución:

Antes de comenzar a derivar, podemos simplificar al argumento del logaritmo aplicando la siguiente propiedad:

\mathrm{ln}{x}^{n}=n\mathrm{ln}x

Aplicando a la función nos queda:

f\left(x\right)=\mathrm{ln}\sqrt{{x}^{2}+1}=\frac{1}{2}\mathrm{ln}\left({x}^{2}+1\right)

Empleamos la fórmula de la derivada del logaritmo:

{f}^{\text{'}}\left(x\right)=\frac{1}{2}\cdot \frac{{\left({x}^{2}+1\right)}^{\text{'}}}{{x}^{2}+1}

Resolvemos la derivada indicada.

{f}^{\text{'}}\left(x\right)=\frac{1}{2}\cdot \frac{{\left({x}^{2}+1\right)}^{\text{'}}}{{x}^{2}+1}=\frac{1}{2}\cdot \frac{2x}{{x}^{2}+1}=\frac{x}{{x}^{2}+1}

\therefore {f}^{\text{'}}\left(x\right)=\frac{x}{{x}^{2}+1}

La respuesta correcta es el inciso b).