Vamos con la cuarta parte del examen simulacro de la guía EXANI II de Cálculo Diferencial e Integral. En este artículo, resolveremos desde el reactivo 31 hasta el 40.

Si un reactivo parece complejo, déjalo y pasa al siguiente. Es importante que mantengas la concentración mientras estudias.
Reactivo 31
Calcule la siguiente integral indefinida.
\int \sqrt{x}\left({x}^{2}-2x\right)dx
- I=\frac{2}{7}{x}^{\frac{7}{2}}-\frac{4}{5}{x}^{\frac{5}{2}}+C
- I=\frac{2}{7}{x}^{\frac{7}{2}}-\frac{4}{5}{x}^{\frac{5}{2}}
- I=\frac{2}{7}{x}^{\frac{7}{2}}+\frac{4}{5}{x}^{\frac{5}{2}}+C
Solución:
Para resolver esta integral, iniciamos expresando a la raíz como potencia y luego resolvemos la distributiva del integrando.
\int \sqrt{x}\left({x}^{2}-2x\right)dx=\int {x}^{\frac{1}{2}}\left({x}^{2}-2x\right)dx
Resolviendo la distributiva:
\int {x}^{\frac{1}{2}}\left({x}^{2}-2x\right)dx=\int \left({x}^{\frac{1}{2}}\cdot {x}^{2}-2{x}^{\frac{1}{2}}\cdot x\right)dx=\int \left({x}^{5/2}-2{x}^{\frac{3}{2}}\right)dx
Separamos en dos integrales aplicando la propiedad de la integral de la suma.
\int \left({x}^{5/2}-2{x}^{\frac{3}{2}}\right)dx=\int {x}^{5/2}dx-2\int {x}^{3/2}dx
Integramos aplicando la fórmula de la integral de una potencia en ambos términos.
\int {x}^{5/2}dx-2\int {x}^{\frac{3}{2}}dx=\frac{{x}^{\frac{5}{2}+1}}{\frac{5}{2}+1}-2\frac{{x}^{\frac{3}{2}+1}}{\frac{3}{2}+1}+C
Simplificando nos queda que:
\int \sqrt{x}\left({x}^{2}-2x\right)dx=\frac{2}{7}{x}^{\frac{7}{2}}-\frac{4}{5}{x}^{\frac{5}{2}}+C
Indicamos como respuesta correcta al inciso a).
Reactivo 32
Dada la pendiente de la recta tangente a una curva m\left(x\right)=4x-3 , obtenga la expresión de la curva si el punto de tangencia es \left(1, 2\right) .
- y=4{x}^{2}-3x
- y=2x-\frac{3}{2}
- y=2{x}^{2}-3x+3
Solución:
Para resolver este problema, debemos recordar la teoría detrás de las integrales y su conexión con las derivadas. Iniciemos indicando que la derivada de una función en un punto, es igual a la pendiente de la recta tangente en dicho punto.
m\left(x\right)=\frac{df}{dx}
Por lo tanto:
\frac{df\left(x\right)}{dx}=4x-3
Para obtener a la función, debemos integrar respecto de x en ambos lados de la igualdad.
\int \frac{df\left(x\right)}{dx}dx=\int \left(4x-3\right)dx
Simplificando nos queda:
\int df\left(x\right)=\int \left(4x-3\right)dx\to f\left(x\right)=\int \left(4x-3\right)dx
Encontramos a la familia de funciones resolviendo la integral.
f\left(x\right)=\int \left(4x-3\right)dx=4\int xdx-3\int dx=\frac{4{x}^{2}}{2}-3x+C
Finalmente:
F\left(x\right)=2{x}^{2}-3x+C
Esta es la familia de curvas en la que se encuentra f\left(x\right) . Sustituimos los valores del punto dado para calcular el valor de C .
F\left(1\right)=2\to 2=2{\left(1\right)}^{2}-3\left(1\right)+C
Despejamos a C .
C=2-2+3=3
Sustituimos en la familia de curvas:
f\left(x\right)=2{x}^{2}-3x+3
Comparando con los incisos, concluimos que la respuesta correcta es c).
Reactivo 33
La demanda en México para determinado producto tiene un incremento de 500+600\sqrt{t} cada año. Si la demanda actual es de 120.000 y el tiempo t se mide en años, ¿cuánta demanda habrá en 4 años?
- 122.200 unidades
- 125.200 unidades
- 132.200 unidades
Solución:
En los problemas de variaciones (como el de este caso), el problema indica en lenguaje natural cuál es la derivada de la función original mediante frases como: el delta de variación es, los incrementos … ocurren cada … o la tasa de variación de … respecto de … es.
Para nosotros, la derivada de la función de demanda es 500+600\sqrt{t} , mientras que la variable t corresponde al tiempo medido en años.
\frac{dD\left(t\right)}{dt}=500+600\sqrt{t}
Integramos para obtener la función de demanda.
D\left(t\right)=\int \left(500+600\sqrt{t}\right)dt=\int 500dt+\int 600\sqrt{t}dt
Expresamos a la raíz como potencia e integramos.
500\int dt+600\int {t}^{\frac{1}{2}}dt=500t+\frac{1200{t}^{\frac{3}{2}}}{3}+C
D\left(t\right)=500t+400{t}^{\frac{3}{2}}+C
Esta es la familia de curvas de demanda. Para encontrar la correspondiente al problema, debemos calcular el valor de C . El enunciado nos dice que la demanda actual es de 120.000, es decir, que la demanda en el año t=0 \mathrm{a}\mathrm{ñ}\mathrm{o}\mathrm{s} es igual a 120.000.
Sustituimos:
12000=500\left(0\right)+400{\left(0\right)}^{3/2}+C\to C=120000
D\left(t\right)=500t+400{t}^{\frac{3}{2}}+120000
Finalmente, evaluamos a la función de demanda en t=4 .
D\left(4\right)=500\left(4\right)+400{\left(4\right)}^{3/2}+120000=125200
En el año 4, la demanda del producto será de 125,200 unidades.
La respuesta correcta es el inciso b).
Reactivo 34
Identifique el cambio de variables que resuelve la siguiente integral.
\int \frac{{y}^{2}}{\sqrt{1-{y}^{6}}}dy
- u={y}^{2}
- u=y
- u={y}^{3}
Solución:
Recordemos que, para aplicar un cambio de variables, se debe encontrar en el integrando y en forma de producto, la derivada de la expresión que queremos cambiar. Examinando al integrando, vemos que tenemos dos posibles derivadas para el cambio:
dz={y}^{2}dy
dz=\frac{1}{\sqrt{1-{y}^{6}}}dy
Descartamos la segunda. Para que la primera sea la derivada de algún cambio de variable, la expresión original debería ser {y}^{3} . Podemos reacomodar al término {y}^{6} dentro de la raíz como potencia de una potencia {\left({y}^{3}\right)}^{2} .
\int \frac{{y}^{2}}{\sqrt{1-{y}^{6}}}dy=\int \frac{{y}^{2}}{\sqrt{1-{\left({y}^{3}\right)}^{2}}}dy
De esta manera, aplicamos el cambio sobre {y}^{3} .
z={y}^{3}\to dz=3{y}^{2}dy\to \frac{1}{3}dz={y}^{2}dy
Aplicando el cambio la función quedaría:
\frac{1}{3}\int \frac{1}{\sqrt{1-{z}^{2}}}dz
Concluimos el ejercicio indicando como respuesta correcta al inciso c).
Reactivo 35
Calcule la integral indicada aplicando cambio de variables.
\int \frac{\mathrm{ln}\left(\mathrm{ln}x\right)}{x\mathrm{ln}x}dx
- I=\frac{1}{2}{\left[\mathrm{ln}\left(\mathrm{ln}x\right)\right]}^{2}+C
- I={\left[\mathrm{ln}\left(\mathrm{ln}x\right)\right]}^{2}+C
- I=\frac{1}{2}\left[\mathrm{ln}\left(\mathrm{ln}x\right)\right]+C
Solución:
Iniciemos calculando la derivada del numerador.
{\left[\mathrm{ln}\left(\mathrm{ln}x\right)\right]}^{\text{'}}=\frac{{\left(\mathrm{ln}x\right)}^{\text{'}}}{\mathrm{ln}x}=\frac{\frac{1}{x}}{\mathrm{ln}x}=\frac{1}{x\mathrm{ln}x}
Este diferencial lo podemos obtener del integrando:
\int \frac{\mathrm{ln}\left(\mathrm{ln}x\right)}{x\mathrm{ln}x}dx=\int \mathrm{ln}\left(\mathrm{ln}x\right)\frac{1}{x\mathrm{ln}x}dx
Aplicamos el cambio de variables sobre \mathrm{ln}\left(\mathrm{ln}x\right) .
z=\mathrm{ln}\left(\mathrm{ln}x\right)\to dz=\frac{1}{x\mathrm{ln}x}dx
\int \frac{\mathrm{ln}\left(\mathrm{ln}x\right)}{x\mathrm{ln}x}dx\to \int zdz
Integrando nos queda:
\int zdz=\frac{{z}^{2}}{2}+C
Devolvemos el cambio de variables:
\frac{{z}^{2}}{2}+C\to \frac{{\left[\mathrm{ln}\left(\mathrm{ln}x\right)\right]}^{2}}{2}+C
Finalmente:
\int \frac{\mathrm{ln}\left(\mathrm{ln}x\right)}{x\mathrm{ln}x}dx=\frac{{\left[\mathrm{ln}\left(\mathrm{ln}x\right)\right]}^{2}}{2}+C
La respuesta correcta es el inciso a).
Reactivo 36
¿Cuál de las siguientes opciones corresponde con el cambio de variables relacionado con el método de integración por partes?
- \int udv=\int vdu-uv
- \int udv=uv-\int vdu
- \int udv=udv-vdu
Solución:
El método de integración por partes, sale de aplicar integración a la fórmula de la derivada de un producto.
\frac{d\left[u\cdot v\right]}{dx}=\frac{du}{dx}v+\frac{dv}{dx}u\to d\left(u\cdot v\right)=vdu+udv
Integrando nos queda:
\int d\left(u\cdot v\right)=\int vdu+\int udv\to u\cdot v=\int vdu+\int udv
Despejando al término \int udv obtenemos:
\int udv=uv-\int vdu
La fórmula de integración por partes. Debido al procedimiento anterior, el método es realmente un cambio de variables con algunos artificios matemáticos. La respuesta correcta es el inciso b).
Reactivo 37
Calcule la siguiente integral, teniendo en cuenta que debe aplicar el método de integración por partes.
\int \frac{\mathrm{ln}x}{x\sqrt{x}}dx
- -\frac{2}{\sqrt{x}}\mathrm{ln}x-\frac{4}{\sqrt{x}}+C
- \frac{2}{\sqrt{x}}\mathrm{ln}x+\frac{4}{\sqrt{x}}+C
- -\frac{1}{\sqrt{x}}\mathrm{ln}x-\frac{2}{\sqrt{x}}+C
Solución:
Examinando la función integrando, queda claro que u debe ser \mathrm{ln}x , debido a que esta función se simplifica cuando la derivamos. Nos queda entonces que dv será \frac{1}{x\sqrt{x}}dx .
u=\mathrm{ln}x\to du=\frac{1}{x}dx
dv=\frac{1}{x\sqrt{x}}dx\to v=\int \frac{1}{x\sqrt{x}}dx
Expresamos al integran como una potencia.
v=\int \frac{1}{x\sqrt{x}}dx=\int \frac{1}{{x}^{3/2}}dx=\int {x}^{-3/2}dx
Integramos aplicando la fórmula de la integral de una potencia.
\int {x}^{-3/2}dx=-2{x}^{-1/2}
Finalmente:
v=-2{x}^{-1/2}
Aplicamos la fórmula de integración por partes.
\int \frac{\mathrm{ln}x}{x\sqrt{x}}dx=-2\frac{\mathrm{ln}x}{\sqrt{x}}+2\int \frac{1}{x\cdot {x}^{\frac{1}{2}}}dx=-2\frac{\mathrm{ln}x}{\sqrt{x}}+2\int {x}^{-\frac{3}{2}}dx
-2\frac{\mathrm{ln}x}{\sqrt{x}}+2\int {x}^{-\frac{3}{2}}dx=-2\frac{\mathrm{ln}x}{\sqrt{x}}-2\left(2{x}^{-\frac{1}{2}}\right)+C=-2\frac{\mathrm{ln}x}{\sqrt{x}}-\frac{4}{\sqrt{x}}+C
Finalmente:
\int \frac{\mathrm{ln}x}{x\sqrt{x}}dx=-2\frac{\mathrm{ln}x}{\sqrt{x}}-\frac{4}{\sqrt{x}}+C
La respuesta correcta es el inciso a).
Reactivo 38
¿Cuál es el resultado de calcular la siguiente integral?
\int \mathrm{sin}\left(3x\right)\mathrm{cos}\left(2x\right)dx
- I=-3\mathrm{cos}\left(3x\right)+2\mathrm{sin}\left(2x\right)+C
- I=-\frac{1}{10}\mathrm{cos}\left(5x\right)-\frac{1}{2}\mathrm{cos}x+C
- I=-\mathrm{cos}\left(5x\right)-\frac{1}{2}\mathrm{cos}x+C
Solución:
Examinando la integral, vemos que no es posible aplicar un cambio de variables debido a que los argumentos son distintos. Podemos simplificar mediante la identidad del producto del coseno por el seno.
\mathrm{cos}a\mathrm{sin}b=\frac{\mathrm{sin}\left(b+a\right)+\mathrm{sin}\left(b-a\right)}{2}
Sustituyendo los argumentos correspondientes:
\mathrm{cos}2x\mathrm{sin}3x=\frac{\mathrm{sin}\left(3x+2x\right)+\mathrm{sin}\left(3x-2x\right)}{2}=\frac{\mathrm{sin}\left(5x\right)+\mathrm{sin}\left(x\right)}{2}
\mathrm{cos}2x\mathrm{sin}3x=\frac{\mathrm{sin}\left(5x\right)}{2}+\frac{\mathrm{sin}\left(x\right)}{2}
Sustituimos en la integral.
\int \mathrm{sin}\left(3x\right)\mathrm{cos}\left(2x\right)dx=\int \frac{\mathrm{sin}\left(5x\right)}{2}+\frac{\mathrm{sin}\left(x\right)}{2}dx=\int \frac{\mathrm{sin}\left(5x\right)}{2}dx+\int \frac{\mathrm{sin}\left(x\right)}{2}dx
Estas integrales si son inmediatas.
\int \frac{\mathrm{sin}\left(5x\right)}{2}dx+\int \frac{\mathrm{sin}\left(x\right)}{2}dx=-\frac{1}{10}\mathrm{cos}\left(5x\right)-\frac{1}{2}\mathrm{cos}\left(x\right)+C
Finalmente:
\int \mathrm{sin}\left(3x\right)\mathrm{cos}\left(2x\right)dx=-\frac{1}{10}\mathrm{cos}\left(5x\right)-\frac{1}{2}\mathrm{cos}\left(x\right)+C
Comparando con los incisos, la respuesta correcta es el b).
Reactivo 39
Calcule la siguiente integral, aplicando la identidad pitagórica en términos de la tangente y la secante, cuando sea necesario, apoyado en un cambio de variable que le sea conveniente.
\int {\mathrm{tan}}^{\frac{3}{2}}x{\mathrm{sec}}^{4}xdx
- I=\frac{2}{3}{\mathrm{tan}}^{\frac{5}{2}}x+\frac{1}{4}{\mathrm{sec}}^{5}x+C
- I=\frac{2}{5}{\mathrm{tan}}^{\frac{5}{2}}x+\frac{2}{9}{\mathrm{tan}}^{\frac{9}{2}}x+C
- I={\mathrm{tan}}^{\frac{5}{2}}x+\frac{2}{3}{\mathrm{tan}}^{\frac{3}{2}}x+C
Solución:
La identidad pitagórica en términos de la secante y la tangente es:
{\mathrm{tan}}^{2}x+1={\mathrm{sec}}^{2}x
Vamos a expresar a la cuarta potencia de la secante como el producto de dos secantes al cuadrado.
\int {\mathrm{tan}}^{\frac{3}{2}}x{\mathrm{sec}}^{4}xdx=\int {\mathrm{tan}}^{\frac{3}{2}}x{\mathrm{sec}}^{2}x{\mathrm{sec}}^{2}xdx
Sustituimos a una de las secantes al cuadrado por la identidad.
\int {\mathrm{tan}}^{\frac{3}{2}}x{\mathrm{sec}}^{2}x{\mathrm{sec}}^{2}xdx=\int {\mathrm{tan}}^{\frac{3}{2}}x\left({\mathrm{tan}}^{2}x+1\right){\mathrm{sec}}^{2}xdx
Ahora, vamos a aplicar el cambio de variables a la tangente.
z=\mathrm{tan}x\to dz={\mathrm{sec}}^{2}xdx
Aplicamos el cambio de variables.
\int {\mathrm{tan}}^{\frac{3}{2}}x\left({\mathrm{tan}}^{2}x+1\right){\mathrm{sec}}^{2}xdx\to \int {z}^{\frac{3}{2}}\left({z}^{2}+1\right)dz
Esta integral puede resolverse de forma inmediata.
\int {z}^{\frac{3}{2}}\left({z}^{2}+1\right)dz=\int {z}^{\frac{3}{2}}\cdot {z}^{2}dz+\int {z}^{\frac{3}{2}}dz=\int {z}^{\frac{7}{2}}dz+\int {z}^{\frac{3}{2}}dz
\int {z}^{\frac{7}{2}}dz+\int {z}^{\frac{3}{2}}dz=\frac{2}{9}{z}^{9/2}+\frac{2}{5}{z}^{5/2}+C
Devolvemos el cambio de variables:
\frac{2}{9}{z}^{9/2}+\frac{2}{5}{z}^{5/2}+C\to \frac{2}{9}{\mathrm{tan}x}^{9/2}+\frac{2}{5}{\mathrm{tan}x}^{5/2}+C
Finalmente:
\int {\mathrm{tan}}^{\frac{3}{2}}x{\mathrm{sec}}^{4}xdx=\frac{2}{9}{\mathrm{tan}x}^{9/2}+\frac{2}{5}{\mathrm{tan}x}^{5/2}+C
La respuesta correcta es el inciso b).
Reactivo 40
Calcule la siguiente integral utilizando sustitución trigonométrica.
\int \sqrt{4-{x}^{2}}dx
- I=-\frac{1}{\sqrt{4-{x}^{2}}}+C
- I={\left(4-{x}^{2}\right)}^{\frac{3}{2}}+C
- I=2{\mathrm{sin}}^{-1}\left(\frac{x}{2}\right)+\frac{x}{2}\sqrt{4-{x}^{2}}+C
Solución:
Teniendo en cuenta la expresión del integrando, el triángulo que se construye es el siguiente:
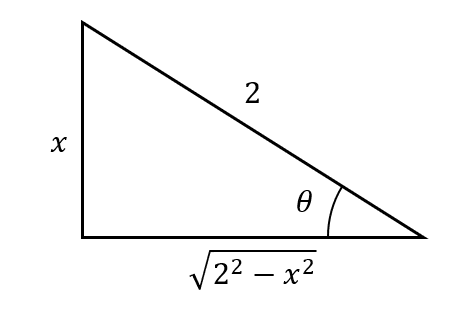
x=2\mathrm{sin}\theta
dx=2\mathrm{cos}\theta d\theta
Aplicando la sustitución trigonométrica:
\int \sqrt{4-{x}^{2}}dx\to 2\int \sqrt{4-{\left(2\mathrm{sin}\theta \right)}^{2}}\mathrm{cos}\theta d\theta =4\int \sqrt{1-{\mathrm{sin}\theta }^{2}}\mathrm{cos}\theta d\theta
Sustituyendo por la identidad pitagórica.
4\int \sqrt{1-{\mathrm{sin}\theta }^{2}}\mathrm{cos}\theta d\theta =4\int \sqrt{{\mathrm{cos}}^{2}\theta }\mathrm{cos}\theta d\theta =4\int \mathrm{cos}\theta \mathrm{cos}\theta d\theta
4\int \mathrm{cos}\theta \mathrm{cos}\theta d\theta =4\int {\mathrm{cos}}^{2}\theta d\theta
Aplicamos la siguiente identidad trigonométrica:
{\mathrm{cos}}^{2}\theta =\frac{1+\mathrm{cos}2\theta }{2}
Sustituimos en la integral.
4\int {\mathrm{cos}}^{2}\theta d\theta =4\int \frac{1+\mathrm{cos}2\theta }{2}d\theta =4\int \left(\frac{1}{2}+\frac{\mathrm{cos}2\theta }{2}\right)d\theta
4\int \left(\frac{1}{2}+\frac{\mathrm{cos}2\theta }{2}\right)d\theta =2\int d\theta +2\int \mathrm{cos}2\theta d\theta
Resolvemos estas dos integrales inmediatas.
2\int d\theta +2\int \mathrm{cos}2\theta d\theta =2\theta +\mathrm{sin}2\theta +C
Devolvemos el cambio de variables despejando a \theta .
x=2\mathrm{sin}\theta \to \theta ={\mathrm{sin}}^{-1}\left(\frac{x}{2}\right)
Además:
\mathrm{sin}2\theta =2\mathrm{sin}\theta \mathrm{cos}\theta
2\theta +\mathrm{sin}2\theta +C=2\theta +2\mathrm{sin}\theta \mathrm{cos}\theta +C
\mathrm{sin}\theta =\frac{x}{2}
\mathrm{cos}\theta =\frac{\sqrt{4-{x}^{2}}}{2}
2\theta +2\mathrm{sin}\theta \mathrm{cos}\theta +C\to 2{\mathrm{sin}}^{-1}\left(\frac{x}{2}\right)+2\frac{x}{2}\frac{\sqrt{4-{x}^{2}}}{2}+C=2{\mathrm{sin}}^{-1}\left(\frac{x}{2}\right)+\frac{x}{2}\sqrt{4-{x}^{2}}+C
Finalmente:
\int \sqrt{4-{x}^{2}}dx=2{\mathrm{sin}}^{-1}\left(\frac{x}{2}\right)+\frac{x}{2}\sqrt{4-{x}^{2}}+C
Concluimos indicando como respuesta correcta al inciso c).

