Examen simulador Guía EXANI-II Cálculo reactivos del 11 al 20

Vamos con la segunda parte del examen simulador, en los reactivos del 11 al 20 del módulo de Cálculo para el Exani II. Estos ejercicios están diseñados para que practiques y refuerces tus habilidades en derivadas y análisis de funciones, conceptos esenciales para el examen de admisión.

Cada reactivo te presenta un desafío distinto, desde el cálculo de derivadas básicas hasta la interpretación gráfica y la resolución de problemas aplicados. Estos ejercicios te ayudarán a consolidar tu comprensión y agilidad para trabajar con funciones y sus derivadas.

Temas que cubrimos en estos reactivos:

1. Derivada de constantes y funciones
2. Reglas de derivación (potencia, producto, cociente)
3. Derivadas implícitas
4. Interpretación gráfica de derivadas
5. Derivada de funciones exponenciales y logarítmicas
6. Aplicación de la regla de la cadena
7. Cálculo de derivadas de funciones trigonométricas y trigonométricas inversas
8. Tercera derivada de una función
9. Derivadas de curvas parametrizadas
10. Pendientes de rectas tangentes a curvas

Prepárate para poner a prueba tu conocimiento y afinar tus habilidades en cálculo. ¡Vamos a resolver estos ejercicios juntos y a prepararnos para el éxito en el examen!

Reactivo 11

Uno de los resultados que se obtiene al calcular la derivada de una constante a partir de la regla general, es que la misma vale cero. ¿Cuál de los siguientes enunciados justifica correctamente este resultado?

1. Porque solo se derivan funciones, no números reales
2. Para calcular la derivada en ese caso, se debe usar la fórmula de la pendiente
3. Porque las constantes tienen el mismo valor sin importar el punto que seleccionemos sobre el eje x

Solución:

Debemos recordar que la derivada mide la velocidad de cambio de una función respecto de su variable independiente, en un punto dado. Debido a que las constantes siempre tienen el mismo valor, no varían en ningún punto. Por esta razón, la derivada de una constante es cero.

Teniendo esto en cuenta y examinando a los incisos, concluimos que la respuesta correcta es c).

Reactivo 12

Asocie la función con su respectiva primera derivada.

1. 1a, 2b, 3c
2. 1c, 2b, 3a
3. 1b, 2c, 3a

Solución:

Vamos a ir derivando cada una de las funciones en la columna izquierda para relacionarla con las derivadas de la derecha.

Primera función.

f\left(x\right)={x}^{2}\to {f}^{\text{'}}\left(x\right)=2x

1c.

Segunda función.

g\left(x\right)={e}^{2x}\to {g}^{\text{'}}\left(x\right)={\left(2x\right)}^{\text{'}}{e}^{2x}=2{e}^{2x}

2b.

Por descarte: 3a. Uniendo todas las respuestas parciales:

1c, 2b, 3a

Indicamos como respuesta correcta al inciso b).

Reactivo 13

Determine la derivada de la siguiente función.

f\left(x\right)=\frac{8}{{\mathrm{ln}}^{2}\left(x-1\right)+4}

1. \frac{{\mathrm{ln}}^{2}\left(x-1\right)}{\mathrm{ln}\left(x-1\right)+4}
2. \frac{1}{2\mathrm{ln}\left(x-1\right)}
3. -\frac{16\mathrm{ln}\left(x-1\right)}{{\left[{\mathrm{ln}}^{2}\left(x-1\right)+4\right]}^{2}\left(x-1\right)}

Solución:

Antes de iniciar a derivar, vamos a reescribir el logaritmo al cuadrado del denominador.

f\left(x\right)=\frac{8}{{\mathrm{ln}}^{2}\left(x-1\right)+4}=\frac{8}{{\left[\mathrm{ln}\left(x-1\right)\right]}^{2}+4}

Ahora, iniciamos derivando con la fórmula de un cociente.

{f}^{\text{'}}\left(x\right)={\left[\frac{8}{{\left[\mathrm{ln}\left(x-1\right)\right]}^{2}+4}\right]}^{\text{'}}=\frac{{\left(8\right)}^{\text{'}}\left\{{\left[\mathrm{ln}\left(x-1\right)\right]}^{2}+4\right\}-{\left\{{\left[\mathrm{ln}\left(x-1\right)\right]}^{2}+4\right\}}^{\text{'}}\left(8\right)}{{\left\{{\left[\mathrm{ln}\left(x-1\right)\right]}^{2}+4\right\}}^{2}}

La derivada del 8 es cero y para {\left[\mathrm{ln}\left(x-1\right)\right]}^{2}+4 aplicamos la propiedad de la derivada de una suma.

{f}^{\text{'}}\left(x\right)=\frac{0-\left\{{\left[{\mathrm{ln}\left(x-1\right)}^{2}\right]}^{\text{'}}+{4}^{\text{'}}\right\}\left(8\right)}{{\left\{{\left[\mathrm{ln}\left(x-1\right)\right]}^{2}+4\right\}}^{2}}

Para el término {\mathrm{ln}\left(x-1\right)}^{2} iniciamos derivando como una potencia.

{f}^{\text{'}}\left(x\right)=\frac{-8\left\{{\left[{\mathrm{ln}\left(x-1\right)}^{2}\right]}^{\text{'}}+0\right\}}{{\left\{{\left[\mathrm{ln}\left(x-1\right)\right]}^{2}+4\right\}}^{2}}=\frac{-\left(8\right)\left(2\right){\left[\mathrm{ln}\left(x-1\right)\right]}^{\text{'}}\mathrm{ln}\left(x-1\right)}{{\left\{{\left[\mathrm{ln}\left(x-1\right)\right]}^{2}+4\right\}}^{2}}

Finalmente, la derivada indicada se resuelve aplicando la fórmula del logaritmo.

{f}^{\text{'}}\left(x\right)=\frac{-16\left(\frac{1}{x-1}\right)\mathrm{ln}\left(x-1\right)}{{\left\{{\left[\mathrm{ln}\left(x-1\right)\right]}^{2}+4\right\}}^{2}}

Acomodamos:

{f}^{\text{'}}\left(x\right)=-16\frac{\mathrm{ln}\left(x-1\right)}{\left(x-1\right){\left[{\mathrm{ln}}^{2}\left(x-1\right)+4\right]}^{2}}

Concluimos que la respuesta correcta es el inciso c).

Reactivo 14

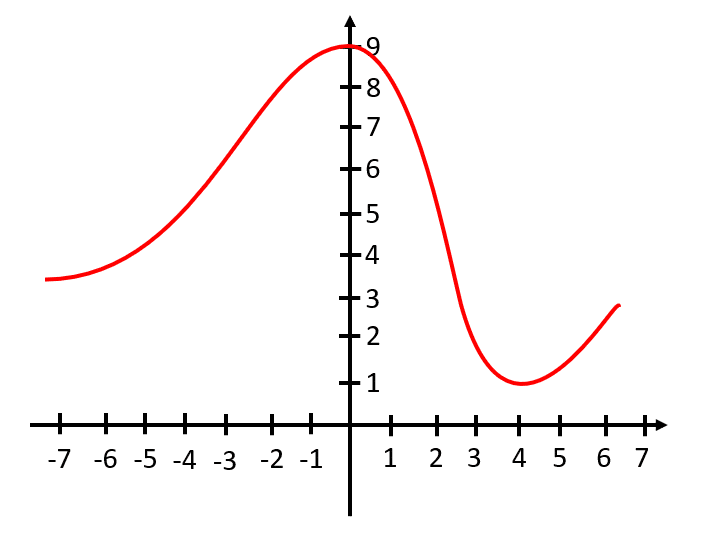
Dada la siguiente gráfica y teniendo en cuenta el intervalo mostrado, indique el o los puntos donde la pendiente a la curva se anula.

1. \left(0, 9\right);\left(4, 1\right)
2. \left(9, 0\right);\left(1, 4\right)
3. \left(-\infty , 3\right), \left(\infty , 3\right)

Solución:

Cuando la derivada de una función que no es una constante se anula, significa que la pendiente de la recta en dicho punto es cero. Una recta con pendiente cero, corresponde a una recta totalmente horizontal.

Examinando la figura, estos puntos son: el máximo relativo en \left(0, 9\right) y el mínimo relativo en \left(4, 1\right) .

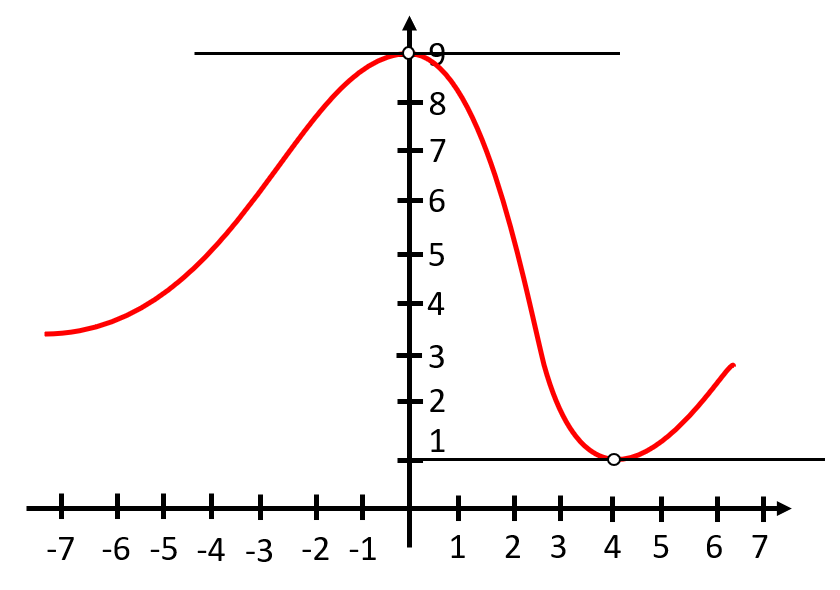
Finalizamos la solución indicando como respuesta correcta al inciso a).

Reactivo 15

Calcula la tercera derivada de la siguiente función.

g\left(x\right)={e}^{{\mathrm{tan}}^{-1}\left(\frac{1}{x}\right)}

1. {g}^{\text{'}}\left(x\right)=\frac{1}{x}{e}^{{\mathrm{tan}}^{-1}\left(\frac{1}{x}\right)}
2. {g}^{\text{'}}\left(x\right)=-\frac{1}{2x}{e}^{{\mathrm{tan}}^{-1}\left(\frac{1}{x}\right)-1}
3. {g}^{\text{'}}\left(x\right)=-\frac{{e}^{{\mathrm{tan}}^{-1}\left(\frac{1}{x}\right)}}{{x}^{2}+1}

Solución:

Para derivar la función del enunciado, debemos aplicar la regla de la cadena. En este caso, la función principal es la exponencial, por tanto, iniciamos derivando con la fórmula de la exponencial.

{g}^{\text{'}}\left(x\right)={\left[{e}^{{\mathrm{tan}}^{-1}\left(\frac{1}{x}\right)}\right]}^{\text{'}}={\left[{\mathrm{tan}}^{-1}\left(\frac{1}{x}\right)\right]}^{\text{'}}{e}^{{\mathrm{tan}}^{-1}\left(\frac{1}{x}\right)}

A la derivada indicada le aplicamos la fórmula de la derivada de la tangente inversa.

{g}^{\text{'}}\left(x\right)=\frac{{\left(\frac{1}{x}\right)}^{\text{'}}}{1+{\left(\frac{1}{x}\right)}^{2}}{e}^{{\mathrm{tan}}^{-1}\left(\frac{1}{x}\right)}

La última derivada indicada se resuelve aplicando la fórmula de la derivada de un cociente.

{g}^{\text{'}}\left(x\right)=\frac{{\left(\frac{1}{x}\right)}^{\text{'}}}{1+{\left(\frac{1}{x}\right)}^{2}}{e}^{{\mathrm{tan}}^{-1}\left(\frac{1}{x}\right)}=\frac{-\frac{1}{{x}^{2}}}{1+\frac{1}{{x}^{2}}}{e}^{{\mathrm{tan}}^{-1}\left(\frac{1}{x}\right)}=-\frac{\frac{1}{{x}^{2}}}{\frac{{x}^{2}+1}{{x}^{2}}}{e}^{{\mathrm{tan}}^{-1}\left(\frac{1}{x}\right)}

{g}^{\text{'}}\left(x\right)=-\frac{1}{{x}^{2}+1}{e}^{{\mathrm{tan}}^{-1}\left(\frac{1}{x}\right)}

Finalizamos indicando como respuesta correcta al inciso c).

Reactivo 16

Calcule la segunda derivada implícita de la siguiente curva.

\frac{{x}^{2}}{4}-\frac{{y}^{2}}{16}=1

1. {y}^{\text{'}\text{'}}=\frac{4{y}^{2}-16{x}^{2}}{{y}^{3}}
2. {y}^{\text{'}\text{'}}=\frac{16{x}^{2}}{{y}^{3}}
3. {y}^{\text{'}\text{'}}=\frac{1}{{y}^{3}}

Solución:

La derivada de una expresión es implícita, cuando tenemos términos no lineales con la variable dependiente y . En este caso, el término negativo tiene en el denominador {y}^{2} , esta es una forma no lineal de la variable dependiente.

Derivamos una primera vez:

\frac{2x}{4}-\frac{2y{y}^{\text{'}}}{16}=0

Simplificamos y despejamos a {y}^{\text{'}} .

\frac{x}{2}-\frac{y{y}^{\text{'}}}{8}=0\to {y}^{\text{'}}=\frac{4x}{y}

Derivamos una segunda vez:

{y}^{\text{'}\text{'}}=\frac{{\left(4x\right)}^{\text{'}}\left(y\right)-{\left(y\right)}^{\text{'}}\left(4x\right)}{{y}^{2}}=\frac{4y-4x{y}^{\text{'}}}{{y}^{2}}

Sustituimos {y}^{\text{'}}=\frac{4x}{y} .

{y}^{\text{'}\text{'}}=\frac{4y-4x\left(\frac{4x}{y}\right)}{{y}^{2}}=\frac{\frac{4{y}^{2}-16{x}^{2}}{y}}{{y}^{2}}=\frac{4{y}^{2}-16{x}^{2}}{{y}^{3}}

Finalmente:

{y}^{\text{'}\text{'}}=\frac{4{y}^{2}-16{x}^{2}}{{y}^{3}}

Comparando con los incisos, la respuesta correcta es el a).

Reactivo 17

Calcule la derivada de la siguiente función.

y=\frac{\mathrm{sin}x}{{\mathrm{cos}}^{2}x}+\mathrm{ln}\left(\frac{1+\mathrm{sin}x}{\mathrm{cos}x}\right)

1. {y}^{\text{'}}=2{\mathrm{sec}}^{3}x
2. {y}^{\text{'}}=2{\mathrm{sec}}^{2}x
3. {y}^{\text{'}}={\mathrm{sec}}^{3}x

Solución:

Antes de iniciar a derivar, vamos a simplificar aplicando identidades trigonométricas al primer término.

y=\frac{\mathrm{sin}x}{{\mathrm{cos}}^{2}x}+\mathrm{ln}\left(\frac{1+\mathrm{sin}x}{\mathrm{cos}x}\right)=\frac{\mathrm{sin}x}{\mathrm{cos}x}\cdot \frac{1}{\mathrm{cos}x}+\mathrm{ln}\left(\frac{1+\mathrm{sin}x}{\mathrm{cos}x}\right)=\mathrm{tan}x\mathrm{sec}x+\mathrm{ln}\left(\frac{1+\mathrm{sin}x}{\mathrm{cos}x}\right)

y=\mathrm{tan}x\mathrm{sec}x+\mathrm{ln}\left(\frac{1+\mathrm{sin}x}{\mathrm{cos}x}\right)

Iniciamos derivando con la propiedad de la derivada de una suma.

{y}^{\text{'}}={\left[\mathrm{tan}x\mathrm{sec}x+\mathrm{ln}\left(\frac{1+\mathrm{sin}x}{\mathrm{cos}x}\right)\right]}^{\text{'}}={\left(\mathrm{tan}x\mathrm{sec}x\right)}^{\text{'}}+{\left[\mathrm{ln}\left(\frac{1+\mathrm{sin}x}{\mathrm{cos}x}\right)\right]}^{\text{'}}

Para el primer término aplicamos la derivada del producto. En el segundo, la derivada del logaritmo natural.

{y}^{\text{'}}={\left(\mathrm{tan}x\right)}^{\text{'}}\mathrm{sec}x+{\left(\mathrm{sec}x\right)}^{\text{'}}\mathrm{tan}x+\frac{{\left(\frac{1+\mathrm{sin}x}{\mathrm{cos}x}\right)}^{\text{'}}}{\frac{1+\mathrm{sin}x}{\mathrm{cos}x}}

{y}^{\text{'}}={\left(\mathrm{tan}x\right)}^{\text{'}}\mathrm{sec}x+{\left(\mathrm{sec}x\right)}^{\text{'}}\mathrm{tan}x+\frac{\mathrm{cos}x}{1+\mathrm{sin}x}{\left(\frac{1+\mathrm{sin}x}{\mathrm{cos}x}\right)}^{\text{'}}

Aplicamos la derivada de la tangente, de la secante y del cociente respectivamente.

{y}^{\text{'}}={\mathrm{sec}}^{2}x\mathrm{sec}x+{\mathrm{tan}}^{2}x\mathrm{sec}x+\frac{\mathrm{cos}x}{1+\mathrm{sin}x}\cdot \frac{{\left(1+\mathrm{sin}x\right)}^{\text{'}}\left(\mathrm{cos}x\right)-{\left(\mathrm{cos}x\right)}^{\text{'}}\left(1+\mathrm{sin}x\right)}{{\mathrm{cos}}^{2}x}

{y}^{\text{'}}={\mathrm{sec}}^{3}x+{\mathrm{tan}}^{2}x\mathrm{sec}x+\frac{1}{1+\mathrm{sin}x}\cdot \frac{{\mathrm{cos}}^{2}x+\mathrm{sin}x\left(1+\mathrm{sin}x\right)}{\mathrm{cos}x}

{y}^{\text{'}}={\mathrm{sec}}^{3}x+{\mathrm{tan}}^{2}x\mathrm{sec}x+\frac{1}{1+\mathrm{sin}x}\cdot \frac{{\mathrm{cos}}^{2}x+\mathrm{sin}x+{\mathrm{sin}}^{2}x}{\mathrm{cos}x}

Aplicamos la identidad pitagórica.

{y}^{\text{'}}={\mathrm{sec}}^{3}x+{\mathrm{tan}}^{2}x\mathrm{sec}x+\frac{1}{1+\mathrm{sin}x}\cdot \frac{1+\mathrm{sin}x}{\mathrm{cos}x}={\mathrm{sec}}^{3}x+{\mathrm{tan}}^{2}x\mathrm{sec}x+\frac{1}{\mathrm{cos}x}

{y}^{\text{'}}={\mathrm{sec}}^{3}x+{\mathrm{tan}}^{2}x\mathrm{sec}x+\mathrm{sec}x

Extraemos factor común secante de los dos últimos términos.

{y}^{\text{'}}={\mathrm{sec}}^{3}x+\left({\mathrm{tan}}^{2}x+1\right)\mathrm{sec}x

Aplicamos la identidad pitagórica en términos de la secante y la tangente.

{\mathrm{tan}}^{2}x+1={\mathrm{sec}}^{2}x

{y}^{\text{'}}={\mathrm{sec}}^{3}x+{\mathrm{sec}}^{2}x\mathrm{sec}x={\mathrm{sec}}^{3}x+{\mathrm{sec}}^{3}x=2{\mathrm{sec}}^{3}x

Finalmente:

{y}^{\text{'}}=2{\mathrm{sec}}^{3}x

Comparando con los incisos, la respuesta correcta es el a).

Reactivo 18

Calcule la pendiente de la recta tangente a la curva f\left(x\right)={x}^{3}-1 , cuando x=0 .

1. m=1
2. m=3
3. m=0

Solución:

Recordemos que la pendiente de la recta tangente a una curva se obtiene evaluando su derivada en el punto. Teniendo en cuenta lo anterior, debemos calcular la derivada de f\left(x\right) .

{f}^{\text{'}}\left(x\right)={\left({x}^{3}-1\right)}^{\text{'}}=3{x}^{2}

Evaluamos x=0 :

m=3{\left(0\right)}^{2}=0

El que la pendiente de una recta sea cero, indica que es una recta horizontal.

La respuesta correcta es el inciso c).

Reactivo 19

Sea xy-y=2x-1 la expresión de una curva, determine los puntos en los que la pendiente de la recta tangente a ella vale m=-\frac{1}{2} .

1. \left(\sqrt{2}+1,\frac{2\sqrt{2}+1}{\sqrt{2}}\right) y \left(\sqrt{2}-1,\frac{2\sqrt{2}+1}{\sqrt{2}}\right)
2. \left(\sqrt{2}+1,\frac{2\sqrt{2}+1}{\sqrt{2}}\right) y \left(1-\sqrt{2},\frac{2\sqrt{2}-1}{\sqrt{2}}\right)
3. \left(\sqrt{2},\frac{1}{\sqrt{2}}\right) y \left(\sqrt{2}-1,\frac{2\sqrt{2}+1}{\sqrt{2}}\right)

Solución:

Iniciamos encontrando la derivada de la curva, recordemos que m={y}^{\text{'}} . Antes de derivar, vamos a extraer factor común y del miembro de la izquierda:

xy-y=2x-1\to y\left(x-1\right)=2x-1

y=\frac{2x-1}{x-1}

Esta expresión será más sencilla de derivar. Aplicamos la fórmula de la derivada de un cociente:

{y}^{\text{'}}={\left(\frac{2x-1}{x-1}\right)}^{\text{'}}=\frac{{\left(2x-1\right)}^{\text{'}}\left(x-1\right)-{\left(x-1\right)}^{\text{'}}\left(2x-1\right)}{{\left(x-1\right)}^{2}}

Resolvemos las derivadas indicadas.

{y}^{\text{'}}=\frac{2\left(x-1\right)-\left(2x-1\right)}{{\left(x-1\right)}^{2}}=\frac{2x-2-2x+1}{{\left(x-1\right)}^{2}}=-\frac{1}{{\left(x-1\right)}^{2}}

Ahora igualamos la derivada a la pendiente.

-\frac{1}{2}=-\frac{1}{{\left(x-1\right)}^{2}}

Para encontrar los puntos donde la pendiente es igual a -1/2 , resolvemos la ecuación anterior y evaluamos en la función original para encontrar las coordenadas en y .

{\left(x-1\right)}^{2}=2\to x-1=\pm \sqrt{2}

Obtenemos dos posibles resultados:

{x}_{1}=\sqrt{2}+1, {x}_{2}=1-\sqrt{2}

Evaluando en la función original:

{y}_{1}=\frac{2\left(\sqrt{2}+1\right)-1}{\sqrt{2}+1-1}=\frac{2\sqrt{2}+1}{\sqrt{2}}

{y}_{2}=\frac{2\left(1-\sqrt{2}\right)-1}{1-\sqrt{2}-1}=\frac{2\sqrt{2}-1}{\sqrt{2}}

Finalmente, los puntos donde la pendiente de la recta tangente a la curva es igual a -1/2 son:

\left(\sqrt{2}+1,\frac{2\sqrt{2}+1}{\sqrt{2}}\right) y \left(1-\sqrt{2},\frac{2\sqrt{2}-1}{\sqrt{2}}\right)

Podemos comprobar sustituyendo los valores de x en la pendiente.

{y}_{1}^{\text{'}}=-\frac{1}{{\left(\sqrt{2}+1-1\right)}^{2}}=-\frac{1}{{\left(\sqrt{2}\right)}^{2}}=-\frac{1}{2}

{y}_{2}^{\text{'}}=-\frac{1}{{\left(1-\sqrt{2}-1\right)}^{2}}=-\frac{1}{2}

Concluimos el problema indicando como respuesta correcta al inciso b).

Reactivo 20

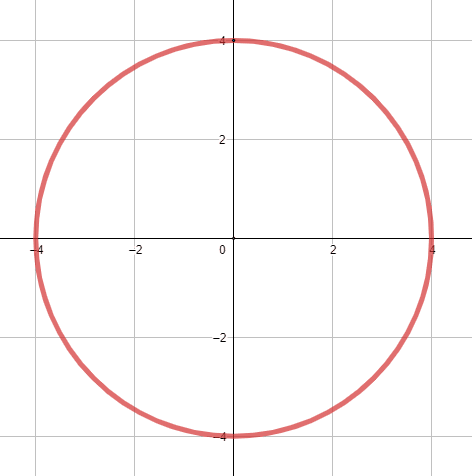
Dada la circunferencia centrada en el origen mostrada en la figura, determine las coordenadas de los puntos donde la pendiente vale \frac{1}{2} .

1. \left(\frac{4}{\sqrt{5}},-\frac{8}{\sqrt{5}}\right) y \left(\frac{4}{\sqrt{5}},\frac{8}{\sqrt{5}}\right)
2. \left(\frac{4}{\sqrt{5}},\frac{8}{\sqrt{5}}\right) y \left(\frac{4}{\sqrt{5}},\frac{8}{\sqrt{5}}\right)
3. \left(\frac{4}{\sqrt{5}},-\frac{8}{\sqrt{5}}\right) y \left(-\frac{4}{\sqrt{5}},\frac{8}{\sqrt{5}}\right)

Solución:

Iniciamos encontrando la ecuación de la circunferencia. A partir de la imagen vemos que el radio es r=4 y que el centro \left(h, k\right)=\left(0, 0\right) .

{x}^{2}+{y}^{2}=16

Derivamos la expresión implícitamente y luego despejamos a {y}^{\text{'}} .

{x}^{2}+{y}^{2}=16\to 2x+2y{y}^{\text{'}}=0

{y}^{\text{'}}=-\frac{x}{y}

Podríamos comenzar despejar a y de la ecuación original y despejar así el valor de x y luego encontrar la coordenada vertical de los puntos; pero este procedimiento es largo. En su lugar, vamos a probar los puntos de cada inciso en la ecuación de la pendiente.

Si el resultado no es 1/2 , entonces pasamos al siguiente inciso.

Primer inciso.

{y}^{\text{'}}=-\frac{\frac{4}{\sqrt{5}}}{-\frac{8}{\sqrt{5}}}=\frac{1}{2}

{y}^{\text{'}}=-\frac{\frac{4}{\sqrt{5}}}{\frac{8}{\sqrt{5}}}=-\frac{1}{2}

El segundo punto da como resultado una pendiente negativa.

Segundo inciso.

Los puntos son iguales y ambas coordenadas son positivas, el resultado será negativo.

Tercer inciso.

{y}^{\text{'}}=-\frac{\frac{4}{\sqrt{5}}}{-\frac{8}{\sqrt{5}}}=\frac{1}{2}

{y}^{\text{'}}=-\frac{-\frac{4}{\sqrt{5}}}{\frac{8}{\sqrt{5}}}=\frac{1}{2}

El inciso c) es la respuesta correcta.