¡Vamos a seguir con más ejercicios del EXANI II! Ahora vamos a resolver los reactivos del 21 al 30 del módulo de aritmética. Estos problemas son ideales para poner a prueba tus habilidades y prepararte mejor para el examen de admisión.

Aquí encontrarás una mezcla de situaciones que te ayudarán a repasar conceptos clave y te darán una idea clara del tipo de preguntas que puedes esperar en la prueba.
Temas que cubrimos en estos reactivos:
- Velocidad y tiempo
- Proporcionalidad directa
- Ganancias y pérdidas
- Divisibilidad y reglas de los números
- Porcentajes
- Traducción de frases a expresiones matemáticas
- Razones de crecimiento
- Máximo común divisor
Con esta selección, podrás practicar una amplia variedad de ejercicios, desde problemas de carreras hasta análisis de ganancias y proporciones. ¡Empecemos a resolverlos!
Reactivo 21
En una carrera de Fórmula 1, un corredor A se dirige por la recta final a una razón de 120 kilómetros por hora y el corredor en segundo lugar B, tiene una distancia con el primero de 20 metros y se desplaza a razón de 130 kilómetros por hora.
Si desde el momento en que se toman estos datos el corredor A está a 50 metros de la meta, ¿quién ganará la competición?
- Gana el corredor A
- Gana el corredor B
- Llegan empatados
Solución:
Hagamos una representación gráfica de la posición que tienen los corredores en ese instante.
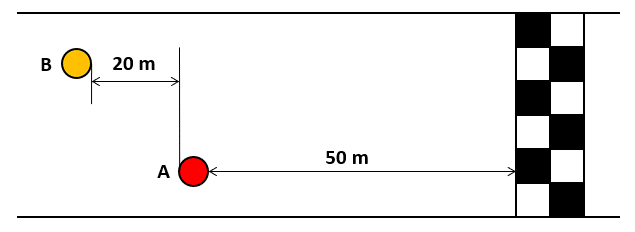
Con esto, sabemos que el corredor A está a 50 metros de la meta, mientras que el B se encuentra a 70 metros. Podemos calcular el tiempo que tardará cada uno en llegar a la meta, teniendo en cuenta la velocidad de cada uno.
Tiempo del corredor A.
120\frac{\mathrm{k}\mathrm{m}}{\mathrm{h}}\to {t}_{A}=\frac{50}{120}=0.4166 \mathrm{h}
Tiempo del corredor B.
130\frac{\mathrm{k}\mathrm{m}}{\mathrm{h}}\to {t}_{B}=\frac{70}{130}=0.5384 \mathrm{h}
Aunque el corredor B se desplaza a una mayor velocidad, el corredor A tardará menos tiempo. La respuesta correcta es el inciso a).
Reactivo 22
Eliezer le propone a su hermano menor ahorrar juntos para comprar un nuevo videojuego. Han acordado aportar de forma proporcional a sus edades. Si Eliezer tiene 12 años y su hermano menor tiene 8 años, ¿cuánto dinero deberá aportar Eliezer si el videojuego cuesta $3,800?
- $1520
- $2280
- $3000
Solución:
En este caso, la suma de las edades de los hermanos equivale al costo total del videojuego.
20\to 3800
Si Eliezer tiene 12 años, entonces podemos aplicar una regla de tres simple para calcular su aporte.
20\to 3800
12\to x
Nos queda:
x=\frac{12\cdot 3800}{20}=2280\$
Eliezer debe aportar 2280 pesos para la compra del juego con su hermano.
La respuesta correcta es el inciso b).
Reactivo 23
Un comerciante compró cierto cargamento de maíz en 80,000$ pesos y lo vendió para obtener una ganancia de 25,000$. Si el comerciante vendió el maíz a 100$ el kilo, ¿cuántos kilogramos de maíz conformaban el cargamento?
- 1050 kilogramos de maíz
- 1000 kilogramos de maíz
- 1200 kilogramos de maíz
Solución:
Para cualquier producto tenemos un precio de compra PC , un precio de venta PV y una cantidad de unidades n . La ganancia se obtiene como la diferencia:
\mathrm{G}=\mathrm{n}\mathrm{P}\mathrm{V}-\mathrm{n}\mathrm{P}\mathrm{C}
El enunciado nos indica el total que pagó el usuario por la mercancía. Lo llamaremos: precio total de inversión \mathrm{P}\mathrm{T}\mathrm{I} .
\mathrm{G}=\mathrm{n}\mathrm{P}\mathrm{V}-\mathrm{P}\mathrm{T}\mathrm{I}
Tenemos la ganancia, el precio de venta por kilogramo y la inversión total. Despejamos el total de kilogramos adquiridos.
\mathrm{G}=\mathrm{n}\mathrm{P}\mathrm{V}-\mathrm{P}\mathrm{T}\mathrm{I}\to \mathrm{n}=\frac{\mathrm{G}+\mathrm{P}\mathrm{T}\mathrm{I}}{\mathrm{P}\mathrm{V}}
Sustituimos.
\mathrm{n}=\frac{25000+80000}{100}=1050 \mathrm{k}\mathrm{i}\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{r}\mathrm{a}\mathrm{m}\mathrm{o}\mathrm{s}
El comerciante compró un total de 1050 kilogramos de maíz.
La respuesta correcta es el inciso a).
Reactivo 24
Luis y su hermano se asocian para trabajar juntos como albañiles. Ha surgido un nuevo trabajo y la paga es de 12,000$ y la duración es de 10 días. ¿Cuánto dinero gana Luis al día si su hermano gana 500$?
- 500$
- 1200$
- 700$
Solución:
Teniendo la paga total del trabajo y los días de duración del proyecto, calculamos la paga diaria.
\mathrm{P}\mathrm{D}=\frac{12000}{10}=1200\frac{\mathrm{\$}}{\mathrm{d}\mathrm{í}\mathrm{a}}
Si el hermano de Luis gana 500$ diarios, entonces él se queda con lo que resta de los 1200 al día.
\mathrm{L}\mathrm{u}\mathrm{i}\mathrm{s}=1200-500=700\mathrm{\$}
Luis gana 700 pesos al día.
La respuesta correcta es el inciso c).
Reactivo 25
Un número es divisible por nueve si…
- Si es divisible entre 3
- Si la suma de sus dígitos es 9
- Si la suma de sus dígitos es múltiplo de 9
Solución:
El número 9 sólo es divisible por el 3, por sí mismo y por el 1. Teniendo en cuenta los incisos, la respuesta correcta es c).
Reactivo 26
Escriba en lenguaje matemático la siguiente frase en lenguaje natural.
La semiresta de 6 con 3 elevada a la segunda potencia.
- {\left[\frac{6-3}{2}\right]}^{2}
- {\left[\frac{3-6}{2}\right]}^{2}
- \frac{{\left(6-3\right)}^{2}}{2}
Solución:
Vamos a ir analizando la frase por partes hasta convertirla en expresión matemática.
La semiresta de 6 con 3…
La semirresta entre dos números, establece que debemos restarlos y dividirlos entre 2.
\frac{6-3}{2}
… elevada a la segunda potencia.
Debemos elevar al cuadrado a la semiresta de 6 con 3.
{\left(\frac{6-3}{2}\right)}^{2}
Comparando con los incisos, la respuesta correcta es el a).
Reactivo 27
Un instrumento de medición marca en determinado momento 100 psi y, luego de algunos minutos su lectura ha incrementado a 107 psi. ¿En cuánto porcentaje incrementó la medición?
- 10%
- 5%
- 7%
Solución:
Para calcular cualquier diferencia porcentual, empleamos la siguiente fórmula.
{\mathrm{\Delta }}_{\mathrm{\%}}=\frac{\mathrm{N}\mathrm{u}\mathrm{e}\mathrm{v}\mathrm{o}\mathrm{ }\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{o}\mathrm{r}-\mathrm{A}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{g}\mathrm{u}\mathrm{o}\mathrm{ }\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{o}\mathrm{r}}{\mathrm{A}\mathrm{n}\mathrm{t}\mathrm{i}\mathrm{g}\mathrm{u}\mathrm{o}\mathrm{ }\mathrm{v}\mathrm{a}\mathrm{l}\mathrm{o}\mathrm{r}}\cdot 100\%
El nuevo valor es 107 psi y el antiguo valor es igual a 100 psi. Sustituimos.
{\mathrm{\Delta }}_{\mathrm{\%}}=\frac{107-100}{100}\cdot 100\%=\frac{7}{100}\cdot 100\%=7\%
La medición del instrumento se incrementa en un 7%.
La respuesta correcta es el inciso c).
Reactivo 28
A partir del número mostrado a continuación, ¿cuál de las siguientes frases es correcta?
\sqrt[3]{{2}^{4}}
- El resultado es indefinido en los reales
- Dos elevado a cuatro tercios
- Dos elevado a tres cuartos
Solución:
Vamos a ir analizando cada una de las frases en el enunciado, aquella que sea correcta será la respuesta al problema.
El resultado es indefinido en los reales.
Para que el resultado del radical no se encuentre definido en los reales, éste debería arrojar un número imaginario, pero ni el índice de la raíz es par ni el radicando es negativo.
Dos elevado a cuatro tercios.
Si expresamos a la operación como una potencia obtenemos:
\sqrt[3]{{2}^{4}}={\left({2}^{4}\right)}^{\frac{1}{3}}={2}^{\frac{4}{3}}
El inciso b) es la respuesta correcta al problema.
Reactivo 29
La gráfica que se muestra a continuación representa la relación entre voltaje y corriente de una resistencia de carbón convencional.
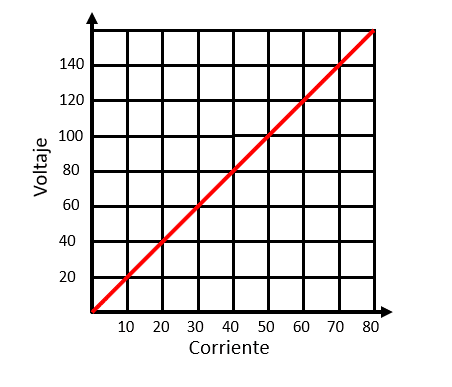
¿Cuál es la razón de crecimiento del voltaje cuando incrementa la corriente?
- 2 voltios por amperio
- 4 amperios por voltio
- 2 amperios por voltio
Solución:
Debido a que la relación entre la corriente y el voltaje es lineal, podemos calcular la razón de incremento como el cociente entre el mínimo cambio del voltaje sobre el mínimo cambio de la corriente.
\frac{20-0}{10-0}=\frac{20}{10}=2\frac{\mathrm{V}\mathrm{o}\mathrm{l}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{s}}{\mathrm{C}\mathrm{o}\mathrm{r}\mathrm{r}\mathrm{i}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{e}}
La razón de cambio es de 2 voltios por amperio.
Indicamos como respuesta correcta al inciso a).
Reactivo 30
La construcción de dos edificaciones en paralelo ha requerido el diseño de un sistema de acueductos para conectar a dichas infraestructuras al sistema de ductos de la ciudad. Desde el nodo más cercano la edificación A se encuentra a 180 metros y la edificación B a 250 metros del mismo nodo.
No deben existir cortes, ya que eso haría frágil el sistema de ductos y por temas económicos, el tubo empleado para la conexión de A se deberá emplear para la conexión de B. ¿Cuál es el máximo tamaño de tubería que debería utilizarse?
- 18 metros
- 10 metros
- 8 metros
Solución:
Aunque el enunciado sea largo, el problema nos solicita que calculemos una longitud de tubería que pueda emplearse tanto para A como para B.
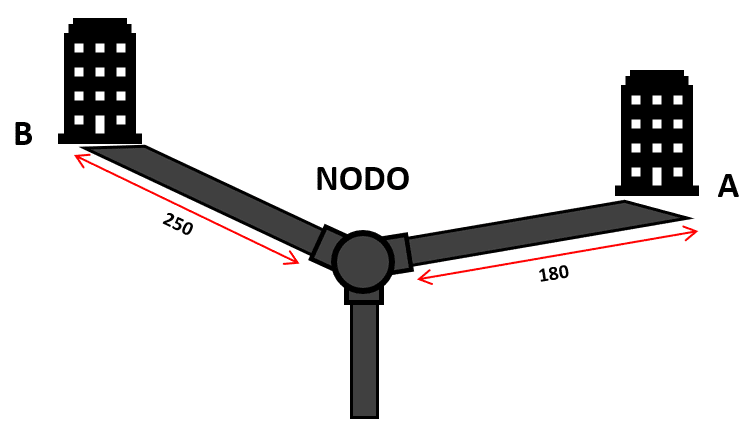
La máxima longitud de tubería para cubrir ambas distancias la encontramos con el máximo común divisor.
\mathrm{M}\mathrm{C}\mathrm{D}\left(180, 250\right)=10
La máxima distancia de tuberías que se puede emplear para los acueductos es de 10 metros. Indicamos como respuesta correcta al inciso b).