Examen simulacro guía EXANI II Pensamiento Matemático V.2 P.2

Continuamos con la solución de la segunda versión del examen simulacro de pensamiento matemático con temas de la guía EXANI II. En esta entrada, resolveremos la segunda parte desde el reactivo 11 hasta el 20.

Resuélvelos por tu cuenta antes de revisar la solución. Utiliza este material para salir de dudas, es necesario que desarrolles tu capacidad de analizar y resolver problemas.

Reactivo 11

Se lanzan dos monedas al aire y se observan sus caras superiores. Determine la probabilidad de obtener águila en ambas.

1. 1/4
2. 1/2
3. 7/8

Solución:

Para este caso, el espacio muestral del experimento aleatorio es el siguiente:

S=\left\{AA, AS, SA, SS\right\}

Es decir, ambas águilas, un águila y otra sol, sol y águila o ambas monedas sol. Examinando, nos damos cuenta que solo hay una posibilidad de obtener águila en ambas mondes. Calculamos la probabilidad como eventos favorables entre el total de eventos.

P\left(AA\right)=\frac{1}{4}

Comparando con las opciones, concluimos que la correcta está en a).

Reactivo 12

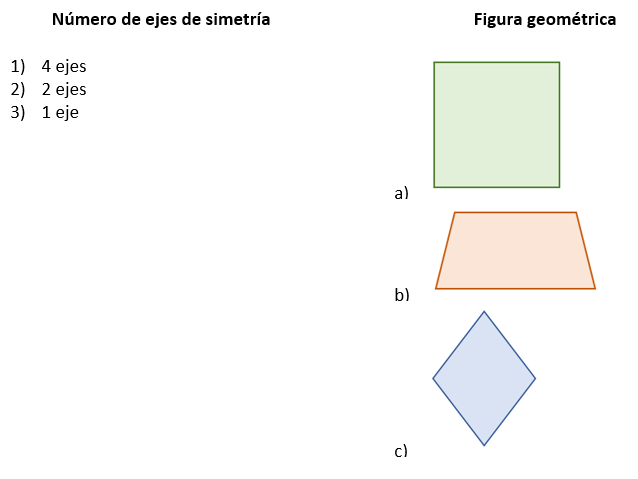
Relaciona el número de ejes de simetría con la figura correspondiente.

1. 1a, 2b, 3c
2. 1b, 2a, 3c
3. 1a, 2c, 3b

Solución:

En este caso, debemos identificar los ejes de simetría que tiene cada figura. Recordemos que un eje de simetría es un segmento de recta dibujado sobre la figura, de tal forma que, al doblar una mitad sobre la otra, ambas partes calcen perfectamente una sobre la otra.

Iremos analizando cada figura de la columna derecha para asociarla con un determinado número en la columna izquierda.

Figura a.

Sobre este cuadrado podemos dibujar 4 ejes de simetría: son diagonales, una línea vertical centrada y otra horizontal, también centrada.

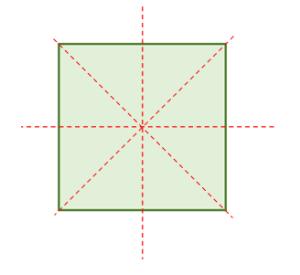
Concluimos entonces que: 1a.

Figura b.

Sin importar como se vea, este trapecio solo posee 1 eje de simetría, un segmento de recta vertical que pasa por su punto medio.

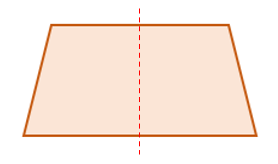
Concluimos entonces que: 3b.

Figura c.

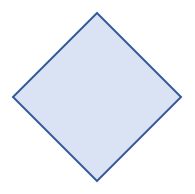
En este último caso, por descarte los ejes de simetría son 2. Esto lo podemos comprobar examinando la figura.

Concluimos que: 2c.

Uniendo todas las respuestas nos queda: 1a, 2c, 3b. Comparando con las opciones, el inciso correcto es el c).

Reactivo 13

María fue a una tienda de maquillaje y compró un producto A que tenía un descuento del 20%. Al llegar a la caja, para pagar con tarjeta de crédito, la tienda le ofreció un descuento adicional del 10%. Al pagar, María se da cuenta que le queda más dinero de lo esperado y decide comprar otro producto B con un descuento del 15%. Debido a que de nuevo pagó con tarjeta de crédito, recibió otro 10% de descuento en la segunda compra.

Si el precio del producto A es el doble del producto B, ¿Cuál fue el descuento total que recibió María por ambas compras?

1. 30.7%
2. 26.5%
3. 45%

Solución:

Debido a la complejidad del enunciado, vamos a darle nombre a los porcentajes para ir calculando todo progresivamente y evitar equivocaciones. Los descuentos del producto A se llamarán 1A, 2A, … y los del producto B 1B, 2B y así sucesivamente.

Además, el ahorro total que percibió María se calcula como: el precio original menos el precio real. Llamaremos a la cuenta actual como CA, para ir ordenando progresivamente los descuentos y CO a la cuenta original sin el descuento.

Comencemos con el producto A, el cual tiene un precio {P}_{A} y, al recibir el primer descuento, la CA queda como:

CA=\left(1-{D}_{1A}\right){P}_{A}; {D}_{1A}=20\%

Luego, por pagar con tarjeta de crédito recibe otro descuento del 10%.

CA=\left(1-{D}_{1A}\right)\left(1-{D}_{2A}\right){P}_{A}

Ahora, compra el producto B que tiene dos descuentos sucesivos aplicados de la misma forma y que se adicionan a la cuenta actual en la tienda.

CA=\left(1-{D}_{1A}\right)\left(1-{D}_{2A}\right){P}_{A}+\left(1-{D}_{1B}\right)\left(1-{D}_{2B}\right){P}_{B}

María ha ahorrado lo que hubiese pagado sin los descuentos, menos la cuenta actual.

Ah=CO-CA

Ah={P}_{A}+{P}_{B}-\left[\left(1-{D}_{1A}\right)\left(1-{D}_{2A}\right){P}_{A}+\left(1-{D}_{1B}\right)\left(1-{D}_{2B}\right){P}_{B}\right]

Empleamos la relación que tenemos del precio entre los productos:

{P}_{A}=2{P}_{B}

Sustituimos.

Ah=2{P}_{B}+{P}_{B}-\left[\left(1-{D}_{1A}\right)\left(1-{D}_{2A}\right)2{P}_{B}+\left(1-{D}_{1B}\right)\left(1-{D}_{2B}\right){P}_{B}\right]

Simplificamos.

Ah={P}_{B}\{3-\left[2\left(1-{D}_{1A}\right)\left(1-{D}_{2A}\right)+\left(1-{D}_{1B}\right)\left(1-{D}_{2B}\right)\right]\}

Sustituimos el valor de los descuentos.

Ah={P}_{B}\{3-\left[2\left(1-0.2\right)\left(1-0.1\right)+\left(1-0.15\right)\left(1-0.1\right)\right]\}

Ah=0.795{P}_{B}

María se ahorró pagar 0.795 veces el precio del producto B (esto también puede expresarse en términos del precio del producto A y sería equivalente). Para encontrar el descuento, dividimos el ahorro entre el precio total expresado en términos de {P}_{B} .

D=\frac{Ah}{{P}_{A}+{P}_{B}}=\frac{0.795{P}_{B}}{3{P}_{B}}=0.265

María obtuvo un descuento del 26.5%.

Comparando con las opciones, escogemos la b) como correcta.

Reactivo 14

Indique cuál de las siguientes oraciones es correcta.

1. Las magnitudes se miden a partir de las unidades
2. A una magnitud se le puede comparar cualquier unidad que corresponda a su naturaleza
3. El tiempo es una unidad y los segundos son una magnitud

 

1. 1, 2
2. 2, 3
3. 3, 1

Solución:

Recordemos que las unidades de medida son patrones con los que se comparan las magnitudes físicas. El metro, la yarda y el pie (por mencionar algunas) son unidades o patrones que empleamos para referirnos a longitudes. Comparamos el patrón del metro con cierta longitud para asociar un número en metros, de la misma forma sucede con el resto de unidades.

Por tanto, analizando las frases, la primera es correcta ya que dice desde otra perspectiva, lo mencionado en el párrafo anterior. La segunda frase menciona lo que comentamos sobre la yarda, el metro y el pie, comparables con cualquier magnitud que represente una longitud.

La tercera frase es errónea. La magnitud es el tiempo y los segundos son la unidad. Concluyendo el análisis decimos que:

1, 2.

La respuesta correcta es la a).

Reactivo 15

Simplifique la siguiente expresión algebraica aplicando las reglas de la potenciación y la radicación correctamente.

\frac{{\left(3{x}^{2}\right)}^{2}{y}^{4}}{3{y}^{2}}

1. \frac{3}{{y}^{3}}
2. 3{x}^{4}{y}^{2}
3. \frac{9{x}^{2}}{{y}^{2}}

Solución:

En este caso, aplicamos las reglas de los exponentes de forma correspondiente. Iniciamos resolviendo {\left(3{x}^{2}\right)}^{2} .

\frac{{\left(3{x}^{2}\right)}^{2}{y}^{4}}{3{y}^{2}}=\frac{9{x}^{4}{y}^{4}}{3{y}^{2}}

Ahora, aplicamos división de potencias de igual base y simplificamos el 9 con el 3.

3{x}^{4}{y}^{2}

Sin más que simplificar, concluimos que la respuesta correcta es la b).

Reactivo 16

Teniendo en cuenta que el lado de cada cuadrado en la cuadrícula mide una unidad (1), determine el área que encierra el contorno mostrado.

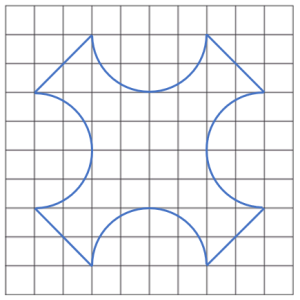
1. 56-8\pi
2. 8\pi -32
3. 34

Solución:

Para encontrar el área que encierra el contorno, debemos identificar las figuras básicas que se forman a partir de ella.

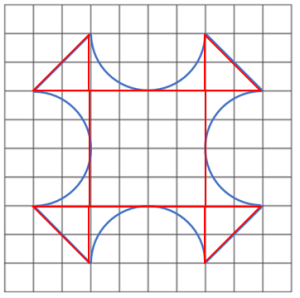
Los contornos marcados en rojo son 4 triángulos rectángulos y un cuadrado. Por otra parte, falta el área de las medias circunferencias, podemos calcular el área del rectángulo en el que se encuentran y restarle el área de la media circunferencia, así obtenemos el área faltante dentro del contorno curvo.

El área encerrada se calcula como:

{A}_{c}=4{A}_{T}+{A}_{cu}+4{A}_{cc}

Donde {A}_{T} es el área de los triángulos, {A}_{cu} es el área del cuadrado y {A}_{cc} es el área del contorno curvo. El área de cada cuadrito en la cuadrícula la llamaremos {a}_{c} .

Área de un triángulo.

{A}_{T}=\frac{1}{2}{a}_{c}+\frac{1}{2}{a}_{c}+{a}_{c}=2{a}_{c}

Área del cuadrado.

{A}_{cu}=16{a}_{c}

Área de un contorno curvo.

{A}_{cc}=8{a}_{c}-\frac{\pi {r}^{2}}{2}

El radio es igual a 2 unidades.

{A}_{cc}=8{a}_{c}-\frac{\pi {\left(2\right)}^{2}}{2}=8{a}_{c}-2\pi 

Área de los cuadrados de la cuadrícula.

{a}_{c}=1

Sustituimos.

{A}_{c}=4\left(2*1\right)+16*1+4\left(8*1-2\pi \right)=24+32-8\pi 

{A}_{c}=56-8\pi 

Comparando con las opciones, indicamos como correcta la a).

Reactivo 17

A partir de las funciones f\left(x\right) y g\left(x\right) , determine: f+g , f-g y fg .

f\left(x\right)=x-3

g\left(x\right)={x}^{2}

1. {x}^{2}+x-3, -{x}^{2}+x-3, {x}^{3}-3x
2. {x}^{2}, 3-{x}^{2}, {x}^{3}
3. 4x+{x}^{2}, -x+3, 3{x}^{3}

Solución:

En este ejercicio, solo debemos aplicar operaciones básicas entre polinomios, tales como la suma, resta y producto, debido a que ambas funciones son polinómicas. Comenzamos con la suma:

f+g=x-3+{x}^{2}={x}^{2}+x-3

Resta de polinomios.

f-g=x-3-{x}^{2}=-{x}^{2}+x-3

Producto de polinomios.

f*g=\left(x-3\right)\left({x}^{2}\right)={x}^{3}-3{x}^{2}

Juntas, las tres respuestas quedan como:

{x}^{2}+x-3, -{x}^{2}+x-3, {x}^{3}-3{x}^{2}

Concluimos que la respuesta correcta es el inciso a).

Reactivo 18

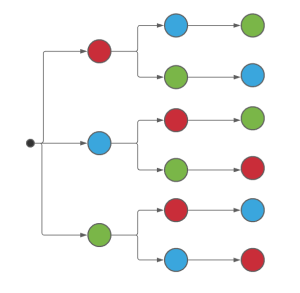
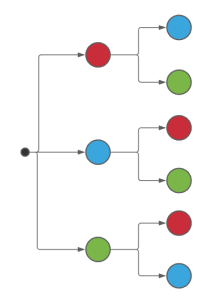
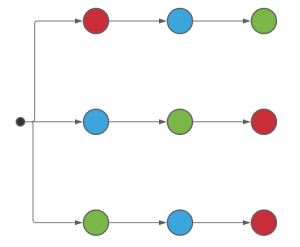
Se colocan 3 bolas de colores en una caja y se le pide a un estudiante que saque las tres bolas una luego de la otra. Si las bolas son de color rojo, verde y azul, ¿cuál es el diagrama de árbol del experimento aleatorio?

1. 
2. 
3. 

Solución:

Para construir el diagrama de árbol correcto, debemos emular que llevamos a cabo el experimento aleatorio indicado, hasta que ya no queden más posibles resultados. Antes de iniciar, es necesario recordar que, al sacar una bola, la cantidad disminuye en 1.

Primera extracción.

Al sacar la primera bola tenemos 3 posibilidades: que sea roja, verde o azul. Esto queda representado como:

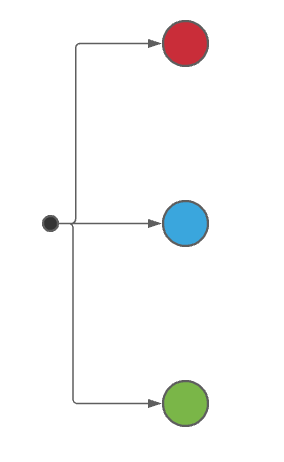
Segunda extracción.

Ahora, en lugar de 3 bolas quedan 2 de los colores que no salieron en la primera extracción. Es decir, quedan rojo y verde si en la primera salió azul. Así con rojo y verde.

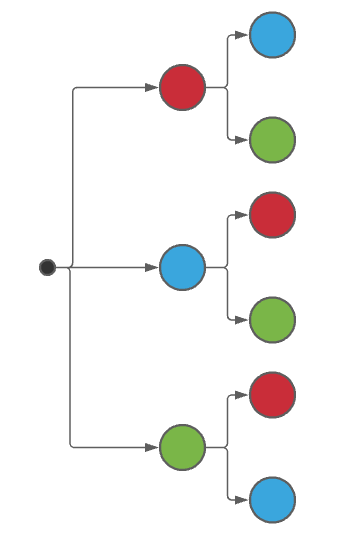
Tercera extracción.

Para la última extracción solo queda una bola, y será la del color no extraído en las anteriores 2 jugadas. El diagrama queda finalmente como:

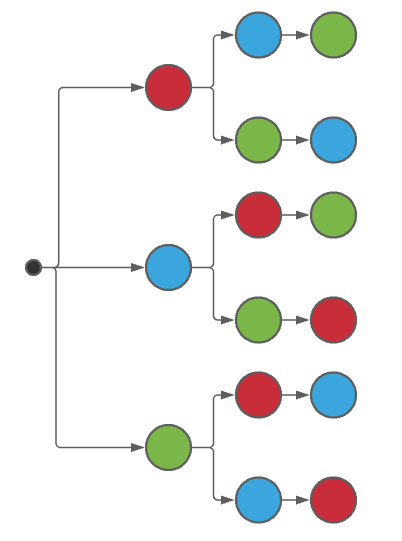
Comparando el diagrama de árbol con las opciones de los incisos, concluimos que la correcta se encuentra en el a).

Reactivo 19

Dado el siguiente sistema de ecuaciones lineales con dos incógnitas, encuentra los valores de x y y que son solución del mismo.

\left\{\begin{array}{c}2x+5y=15\\ 4x+y=21\end{array}\right.

1. x=2, y=-1
2. x=5, y=1
3. x=1, y=-5

Solución:

Para resolver el sistema de ecuaciones, debemos aplicar cualquier método de solución de SEL. En este caso, usaremos el método por reducción. Comenzamos multiplicando la segunda ecuación por -5 y la sumamos con la primera.

-5{E}_{2}: -20x-5y=-105

Sumamos.

{E}_{1}-5{E}_{2}:

2x+5y=15

-20x-5y=-105

-18x=-90\to x=5

Sustituimos este resultado en cualquiera de las ecuaciones para obtener a y . Esta vez lo haremos en la ecuación 2.

4\left(5\right)+y=21\to y=1

\therefore x=5,y=1

Comparando con las opciones, concluimos que la respuesta correcta es la b).

Reactivo 20

Se lanza al aire un dado regular de 6 caras una única vez. ¿Cuál es la probabilidad de obtener como resultado un número menor o igual que tres?

1. 7/8
2. 3/4
3. 1/2

Solución:

Recordemos que, para calcular la probabilidad de cualquier evento, debemos tener dos cosas: los eventos a favor y el total de eventos. Nuestros eventos a favor son todos los números menores o iguales que tres, es decir:

A=\{1, 2, 3\}

El total de eventos es el total de caras del dado, es decir, 6.

S=\left\{1, 2, 3, 4, 5, 6\right\}

Calculamos entonces la probabilidad de A como:

P\left(A\right)=\frac{3}{6}=\frac{1}{2}

Comparando con las opciones, seleccionamos como correcta la c).