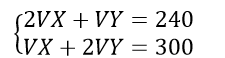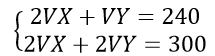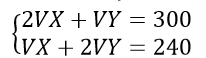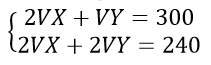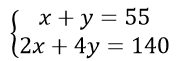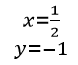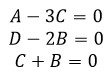Últimos 10 reactivos del examen simulador de Álgebra. En esta quinta parte vamos a resolver los reactivos del 41 al 50, cuando termines te recomiendo que lo intentes de nuevo.

¡Felicitaciones por haber terminado el examen simulacro con éxito! Pero, tu preparación continúa con las demás materias a estudiar. Recuerda que el porcentaje de aspirantes rechazados es muy alto.
Reactivo 41
Identificar el sistema de ecuaciones que resuelve el siguiente problema:
En un hospital se aplican dos vacunas: una dosis de Vx y dos de Vy a un total de 240 individuos del personal médico, a la población en general se aplicarán dos dosis de Vx y una dosis de Vy para un total de 300 personas ¿Cuántas vacunas Vx y Vy deben tener disponibles en el hospital?
Solución:
Extraemos las ecuaciones a partir de las frases en el enunciado:
…una dosis de Vx y dos de Vy a un total de 240 individuos del personal médico…
V X+2 V Y=240
…a la población en general se aplicaran dos dosis de Vx y una dosis de Vy para un total de 300 personas…
2 V X+V Y=300
El SEL quedaría entonces como:
Si comparamos con las opciones que ofrece el problema, la correcta seria la c). Ahora solo queda resolver al SE, para ellos aplicaremos la regla de Cramer.
V X=\frac{\operatorname{det}\left(A_{V X}\right)}{\operatorname{det}(A)}
V Y=\frac{\operatorname{det}\left(A_{V Y}\right)}{\operatorname{det}(A)}
Calculamos el determinante de la matriz del SEL:
A=\left(\begin{array}{ll} 1 & 2 \\ 2 & 1 \end{array}\right) \rightarrow \operatorname{det}(A)=\left|\begin{array}{ll} 1 & 2 \\ 2 & 1 \end{array}\right|=1-4=-3
Se calcula el determinante para cada una de las variables:
A_{V X}=\left(\begin{array}{cc} 240 & 2 \\ 300 & 1 \end{array}\right) \rightarrow \operatorname{det}\left(A_{V X}\right)=\left|\begin{array}{ll} 240 & 2 \\ 300 & 1 \end{array}\right|=240-600=-360
A_{V Y}=\left(\begin{array}{ll} 1 & 240 \\ 2 & 300 \end{array}\right) \rightarrow \operatorname{det}\left(A_{V Y}\right)=\left|\begin{array}{ll} 1 & 240 \\ 2 & 300 \end{array}\right|=300-480=-180
Sustituyendo nos queda que:
V X=\frac{\operatorname{det}\left(A_{V X}\right)}{\operatorname{det}(A)}=\frac{-360}{-3}=120
V Y=\frac{-180}{-3}=60
Reactivo 42
Asociar cada función con su gráfica correspondiente.
| Función | Gráfica | ||
| 1. y=16 x-9610 | A. | 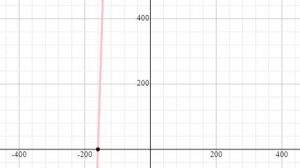
|
|
| 2. y=16 x+9610 | B. | 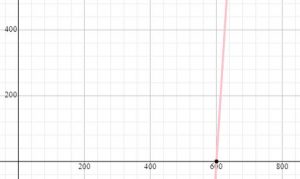
|
|
| 3. y=31 x-4960 | C. | 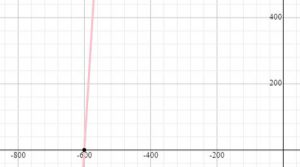
|
|
| 4. y=31 x+4960 | D. | 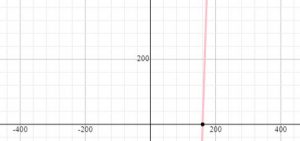
|
|
- 1B, 2C, 3A, 4D
- 1B, 2C, 3D, 4A
- 1D, 2A, 3C, 4B
- 1D, 2A, 3B, 4C
Solución:
Para relacionar correctamente cada función con su gráfica correspondiente, vamos a estudiar los puntos de corte con el eje x , es decir, los valores de x que hacen a y=0 .
Primera función.
y=16 x-9610
Hacemos y=0 y despejamos el valor de x :
16 x-9610=0 \rightarrow x=600.6
Comparando con los cortes en x de las gráficas en la columna derecha, la correcta en este caso sería la B. Por lo tanto: 1B.
Segunda función.
y=16 x+9610
Despejamos el punto de corte con x :
16 x+9610=0 \rightarrow x=-600.6
Este punto de corte corresponde correctamente con la gráfica C en la columna derecha. Por lo tanto: 2C.
Tercera función.
y=31 x-4960
Despejamos el punto de corte con x :
31 x-4960=0 \rightarrow x=160
Este punto de corte corresponde correctamente con la gráfica D en la columna derecha. Por lo tanto: 3D.
Cuarta función.
y=31 x+4960
Despejamos el punto de corte con x :
31 x+4960=0 \rightarrow x=-160
Este punto de corte corresponde correctamente con la gráfica A en la columna derecha. Por lo tanto: 4A.
Concluimos finalmente que: 1B, 2C, 3D, 4A. La respuesta correcta es la b).
Reactivo 43
Identificar el sistema de ecuaciones que permita resolver el siguiente problema:
En un zoológico hay avestruces (x) y leones (y) y en total hay 55 cabezas y 140 patas ¿Cuántos avestruces y cuantos leones hay en el zoológico?
Solución:
Para encontrar las ecuaciones del problema, hay que analizar las frases que relacionan a las variables x y y :
Los leones tienen 4 patas y los avestruces 2, por lo tanto:
2 x+4 y=140
De la misma forma, leones como los avestruces tienen solo una cabeza:
x+y=55
El SE queda entonces como:
\left\{\begin{array}{c} 2 x+4 y=140 \\ x+y=55 \end{array}\right.
Comparando con las opciones del problema, la correcta seria la a). Ahora, procederemos a resolver el SEL empleando el método por reducción:
\left\{\begin{array}{c} (I): 2 x+4 y=140 \\ (I I): x+y=55 \end{array}\right.
Hacemos -2 I I+I :
2 x+4 y=140
-2 x-2 y=-110
2 y=30 \rightarrow y=15
Sustituimos este resultado en II para encontrar el valor de x :
x+y=55 \rightarrow x=55-y
x=40
En el zoológico hay 40 avestruces y 15 leones.
Conoce los aciertos por carrera
Reactivo 44
Para el siguiente sistema de ecuaciones, encuentre los valores de w y z que satisfagan las siguientes igualdades:
\left\{\begin{array}{c} -7 w+2 z=-8 \\ 3 w-5 z=-9 \end{array}\right.
- w=1, z=2
- w=2, z=2
- w=3, z=3
- w=2, z=3
Solución:
Haremos uso del método por igualación para resolver el SEL. Escogemos a la z como variable a despejar en ambas ecuaciones:
-7 w+2 z=-8 \rightarrow z=-4+\frac{7}{2} w
3 w-5 z=-9 \rightarrow z=\frac{9}{5}+\frac{3}{5} w
Ahora, se igualan las ecuaciones y se despeja el valor numérico de w :
-4+\frac{7}{2} w=\frac{9}{5}+\frac{3}{5} w \rightarrow-\frac{3}{5} w+\frac{7}{2} w=\frac{9}{5}+4
-\frac{3}{5} w+\frac{7}{2} w=\frac{9}{5}+4 \rightarrow \frac{29}{10} w=\frac{29}{5}
\therefore w=2
Sustituimos el resultado en cualquiera de las ecuaciones, escogemos la primera:
-7 w+2 z=-8 \rightarrow-7(2)+2 z=-8
-7(2)+2 z=-8 \rightarrow z=3
Concluimos entonces que la respuesta correcta es la d).
Reactivo 45
Resolver el siguiente sistema de ecuaciones: \begin{array}{l} 2 y+\frac{3}{x}=12 \\ 4 y-\frac{2}{x}=8 \end{array}
Solución:
En este caso, haremos uso del método por sustitución. Escogemos a la variable y para despejar de la primera ecuación.
2 y+\frac{3}{x}=12 \rightarrow y=6-\frac{3}{2 x}
Este resultado lo sustituimos en la segunda ecuación:
4\left(6-\frac{3}{2 x}\right)-\frac{2}{x}=8 \rightarrow 24-\frac{6}{x}-\frac{2}{x}=8
24-\frac{6}{x}-\frac{2}{x}=8 \rightarrow 24-\frac{8}{x}=8 \rightarrow 24-8=\frac{8}{x}
24-8=\frac{8}{x} \rightarrow x=\frac{8}{16}=\frac{1}{2}
\therefore x=\frac{1}{2}
Sustituimos ahora en la primera ecuación despejada:
y=6-\frac{3}{2 \frac{1}{2}}=3
\therefore y=3
La respuesta correcta en este caso es la b).
Reactivo 46
Determinar la condición necesaria para que el sistema de ecuaciones lineales tenga una única solución:
\left\{\begin{array}{l} a x+b y=c \\ d x+e y=f \end{array}\right.
- a e-b d \neq 0
- b e-e d \neq 0
- a e+b d \neq 0
- b a-d e \neq 0
Solución:
Haremos uso de la regla de Cramer que dice que: todo sistema de ecuaciones lineales es compatible, determinado, si y solo si el determinante del SEL es diferente de cero:
\operatorname{det}(A) \neq 0
Hallamos el determinante de la matriz A :
A=\left(\begin{array}{ll} a & b \\ d & e \end{array}\right) \rightarrow \operatorname{det}(A)=\left|\begin{array}{ll} a & b \\ d & e \end{array}\right|=a e-d b
\therefore a e-d b \neq 0
Concluimos entonces que la respuesta correcta es la a).
Reactivo 47
Identificar el valor del producto de dos números, considerando lo siguiente:
La suma de dos términos es igual a 2 y la suma de sus cuadrados es igual a 4.
- -4
- -2
- 0
- 2
Solución:
Extraemos las ecuaciones de la frase:
La suma de dos términos es igual a 2…
x+y=2
… La suma de sus cuadrados es igual a 4.
x^{2}+y^{2}=4
Con esto, hemos obtenido un sistema de ecuaciones no lineales, ya que en la segunda ecuación los términos están elevados al cuadrado. Para resolverlo se aplicara el método por sustitución.
Despejamos de la primera ecuación a la variable x :
x+y=2 \rightarrow x=2-y
Ahora sustituimos el resultado en la segunda ecuación:
(2-y)^{2}+y^{2}=4
4-4 y+y^{2}+y^{2}=4 \rightarrow 2 y^{2}-4 y=0
y^{2}-2 y=0
Aplicando la ecuación de segundo grado, nos damos cuenta que hay dos posibles valores para y :
y_{1}=0, y_{2}=2
Encontramos ahora los dos posibles valores para x sustituyendo los dos resultados de y en la primera ecuación:
x=2-y
x_{1}=2-0=2
x_{2}=2-2=0
Quedando los dos puntos de intersección entre ambas ecuaciones como:
P_{1}=(2,0)
P_{2}=(0,2)
En ambos casos, el producto de los números claramente es cero. Concluimos entonces que la respuesta correcta es la c).
Reactivo 48
Identificar la relación correcta entre el valor del discriminante y la cantidad de raíces reales que tendría el polinomio de segundo grado.
- Cero, dos
- Cero, una
- Negativo, una
- Negativo, cero
Solución:
Para este primer problema, solo basta con examinar el análisis antes hecho al discriminante de la ecuación de segundo grado.
Si el discriminante es cero, solo tendríamos una única solución:
\Delta=0 \rightarrow x=\frac{-b}{2 a}
Si el discriminante es negativo, no se tendría ninguna solución en los reales. Por el contrario, las raíces serían complejas, conjugadas:
\Delta<0 \rightarrow x_{1,2}=\frac{-b}{2 a} \pm j \frac{\sqrt{4 a c-b^{2}}}{2 a}
Concluimos con esto que son correctas la b) Cero, una ya que si el discriminante es cero, solo hay una solución real y la d) Negativo, cero porque si el discriminante es negativo la solución ya no está en los reales.
Reactivo 49
Elegir la condición para que la ecuación tenga una única solución a x^{2}+b x+c .
- b^{2}+4 a c>0
- b^{2}-4 a c \neq 0
- b^{2}+4 a c=0
- b^{2}-4 a c=0
Solución:
Similar al problema anterior, la respuesta pasa por analizar al discriminante y lo que sucedería en la fórmula para calcular a las raíces.
Si el discriminante se hace cero, la fórmula para calcular quedaría:
x_{1,2}=\frac{-b \pm \sqrt{0}}{2 a} \rightarrow x=\frac{-b}{2 a}
Es decir, solo habría una única solución. Concluimos entonces que la condición para el discriminante debe ser b^{2}-4 a c=0 . Respuesta correcta la d).
Reactivo 50
Identificar el sistema de ecuaciones para establecer la igualdad de funciones cuadráticas:
f(x)=A\left(2 x^{2}+x\right)+D \text { y } g(x)=3 C x^{2}+2 B x
Solución:
Para que dos polinomios sean iguales, los coeficientes entre términos del mismo grado deben ser iguales. Solo debemos igualar los términos de ambas funciones cuadráticas y así encontraremos el sistema de ecuaciones.
f(x)=A\left(2 x^{2}+x\right)+D=2 A x^{2}+A x+D
g(x)=3 C x^{2}+2 B x
Termino cuadrático:
2 A=3 C \rightarrow 2 A-3 C=0
Termino lineal:
A=2 B \rightarrow A-2 B=0
Termino independiente:
D=0
El sistema de ecuaciones quedaría como:
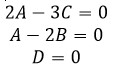
Comparando con las opciones del problema, la correcta sería la c).