¡Seguimos aspirante! En este tutorial resolveremos la cuarta parte del simulacro de física para el examen de ingreso al IPN por el área de Ingeniería y Ciencias Físico-Matemáticas, desde el reactivo 31 hasta el 40.

Resuélvelos por tu cuenta antes de revisar la solución. Además, checa el temario y estudia los fundamentos. Los problemas de física requieren que comprendas muy bien qué leyes debes aplicar.
Reactivo 31
A partir del circuito que se muestra en la figura, calcule la diferencia de potencial en la resistencia {R}_{2} . Tenga en cuenta: {R}_{1}=1 \mathrm{\Omega } , {R}_{2}=2 \mathrm{\Omega } , {R}_{3}=4 \mathrm{\Omega } , {R}_{4}=5 \mathrm{\Omega } .

- 4.21 \mathrm{V}
- 3.21 \mathrm{V}
- 2.21 \mathrm{V}
- 1.21 \mathrm{V}
Solución:
Este circuito puede ser resuelto de dos formas: aplicando las leyes de Kirchhoff a todo el circuito o recurriendo a equivalencias. Debido a que las leyes de Kirchhoff sobre circuitos enteros terminan en grandes sistemas de ecuaciones, la más rápida opción es buscar y aplicar equivalencias en el circuito.
La primera simplificación que podemos hacer, es que la resistencia {R}_{1} no afecta a la malla en la que se encuentra {R}_{2} , ya que {R}_{1} está en paralelo con la fuente. Podemos quitarla del circuito sin afectar el análisis.
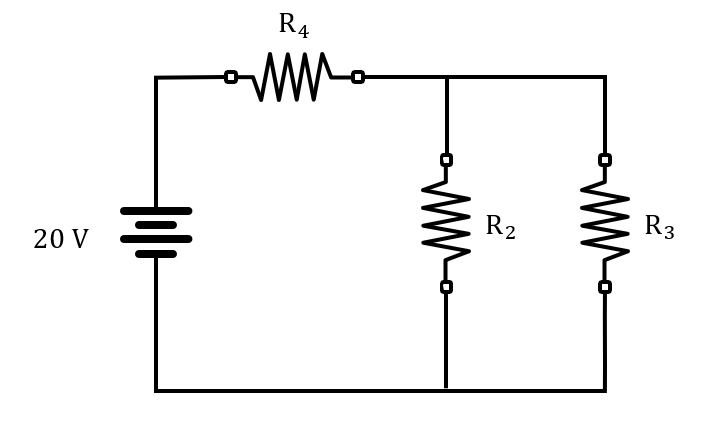
Ahora el circuito es más pequeño, pero tenemos 3 mallas y 2 nodos, aplicar Kirchhoff sigue siendo una opción poco viable.

Podemos calcular la resistencia equivalente entre el paralelo de {R}_{2} y {R}_{3} , luego calcular la corriente de {R}_{4} y finalmente aplicar la ley de mallas.
Equivalente del paralelo de {R}_{2} y {R}_{3} .
{R}_{23}=\frac{{R}_{2}{R}_{3}}{{R}_{2}+{R}_{3}}=1.333 \mathrm{\Omega }
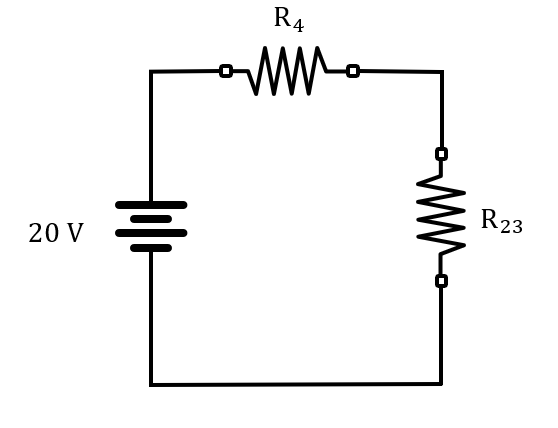
La corriente a través de {R}_{4} es la misma que a través de {R}_{23} .
20=i\left({R}_{4}+{R}_{23}\right)\to i=\frac{20}{{R}_{4}+{R}_{23}}
i=3.16 \mathrm{A}
Ahora analicemos lo siguiente. Por encontrarse en paralelo, las resistencias {R}_{2} y {R}_{3} tienen el mismo voltaje, el cuál corresponde también al voltaje de su equivalente {R}_{23} . Por tanto, solo nos queda aplicar la ley de Ohm sobre {R}_{23} para calcular el voltaje de {R}_{2} .
{v}_{23}={v}_{2}={v}_{3}
{v}_{23}=i{R}_{23}=\left(3.16 \mathrm{A}\right)\left(1.333 \mathrm{\Omega }\right)=4.21 \mathrm{V}
La caída de tensión en {R}_{2} es de 4.21 \mathrm{V} .
La respuesta correcta es el inciso a).
Descubre los aciertos por carrera que necesitas.
Reactivo 32
Calcula la resistencia equivalente para el siguiente arreglo resistivo. Ten en cuenta que {R}_{1}=20 \mathrm{\Omega } , {R}_{2}=30 \mathrm{\Omega } y {R}_{3}=60 \mathrm{\Omega } .

- 20 \mathrm{\Omega }
- 40 \mathrm{\Omega }
- 60 \mathrm{\Omega }
- 80 \mathrm{\Omega }
Solución:
Para calcular la resistencia equivalente entre los terminales del circuito, debemos aplicar resistencias en paralelo y en serie hasta que solo nos quede un solo resistor. Comenzamos resolviendo el paralelo entre {R}_{2} y {R}_{3} .
{R}_{23}=\frac{{R}_{2}{R}_{3}}{{R}_{2}+{R}_{3}}=\frac{\left(30\right)\left(60\right)}{30+60}=20 \mathrm{\Omega }
El circuito quedaría:
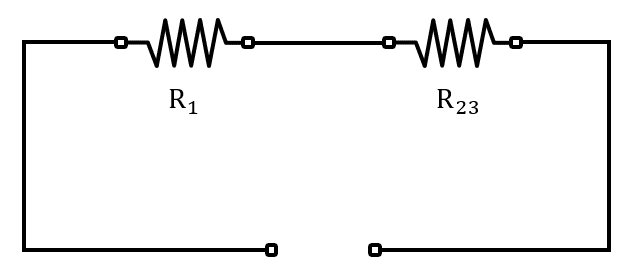
Nota: sería un error haber aplicado resistencia en serie {R}_{1} con {R}_{2} o {R}_{1} con {R}_{3} , debido a que la corriente de {R}_{1} es distinta a la de {R}_{2} y {R}_{3} . Ahora, aplicamos resistencia en serie entre {R}_{1} y {R}_{23} .
{R}_{123}={R}_{1}+{R}_{23}=20 \mathrm{\Omega }+20 \mathrm{\Omega }=40\mathrm{ }\mathrm{\Omega }
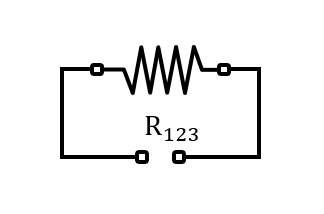
La resistencia equivalente del arreglo es de 40 \mathrm{\Omega } .
Concluimos que la respuesta correcta es el inciso b).
Reactivo 33
Dado el arreglo de capacitores que se muestra en la figura, se busca aumentar la capacitancia equivalente entre los terminales. Las únicas opciones de conexión para un tercer capacitor son: entre los puntos yz o entre los puntos xz.
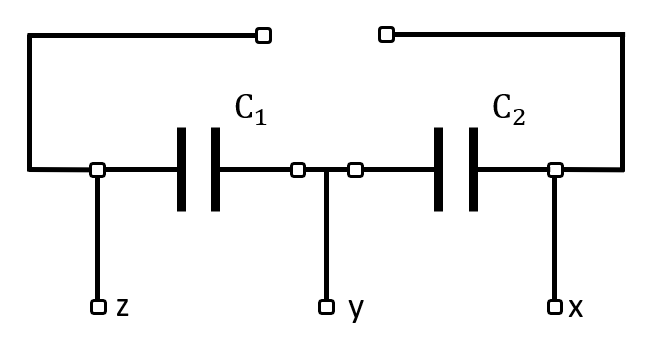
Determine cuál de las conexiones yz o xz, permite lograr el objetivo. Considere: {C}_{1}={C}_{2}=1 \mu F y {C}_{3}=2 \mu F .
- Ninguna
- yz
- Ambas
- xz
Solución:
Para resolver este problema, debemos calcular la capacitancia equivalente para ambas configuraciones, aplicando capacitores en serie y en paralelo. Comenzamos con la conexión entre los puntos yz.

La capacitancia equivalente {C}_{yz} se calcula como el paralelo de 1 y 3 con 2 en serie.
{C}_{yz}=\frac{\left({C}_{1}\left| \right|{C}_{3}\right){C}_{2}}{\left({C}_{1}\left| \right|{C}_{3}\right)+{C}_{2}}
Las capacitancias en paralelo se suman. Luego aplicamos la fórmula para capacitancias en serie.
{C}_{yz}=\frac{3{C}_{2}}{3+{C}_{2}}=\frac{3}{4}\mu F=0.75 \mu F
Vamos ahora con la conexión del capacitor en zx.
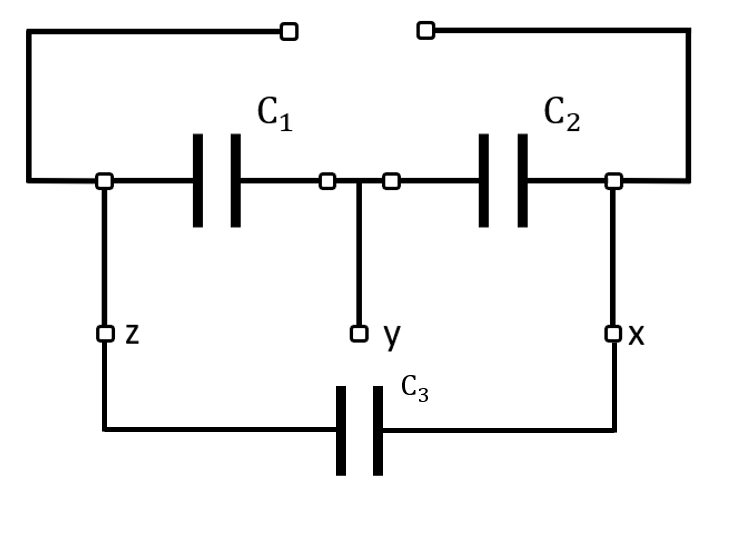
La capacitancia equivalente {C}_{xz} es igual a 1 en serie con 2 y el resultado en paralelo con 3.
{C}_{xz}=\frac{{C}_{1}{C}_{2}}{{C}_{1}+{C}_{2}}+{C}_{3}
Sustituimos.
{C}_{xz}=\frac{\left(1\right)\left(1\right)}{1+1}+2=0.5+2=2.5 \mu F
Comparando ambas capacitancias equivalentes, concluimos que la conexión xz ofrece la mayor capacitancia. Concluimos indicando como respuesta correcta al inciso d).
Conoce todo sobre el siguiente proceso de selección: Convocatoria IPN 2023.
Reactivo 34
Un dispositivo electrónico consume una corriente de 1 Amperio de forma continua, si el mismo tiene una resistencia de 4 Ohm, ¿cuánta potencia consume el dispositivo?
- 2 W
- 3 W
- 4 W
- 5 W
Solución:
En este caso, debemos aplicar la ecuación de potencia eléctrica en cualquiera de sus variantes.
P=V\cdot I={I}^{2}\cdot R=\frac{{V}^{2}}{R}
Debido a que tenemos la resistencia y la corriente, emplearemos la segunda ecuación. Hay que tener en cuenta que todas son equivalentes por la ley de Ohm. Sustituimos.
P={I}^{2}\cdot R={\left(1 \mathrm{A}\right)}^{2}\left(4 \mathrm{\Omega }\right)=4 \mathrm{W}
El dispositivo consume 4 watts de potencia eléctrica.
Concluimos que la respuesta correcta es el inciso c).
Reactivo 35
Relacione los conceptos de electrodinámica con sus respectivas ecuaciones.

- 1B, 2A, 3C, 4D
- 1B, 2C, 3A, 4D
- 1D, 2A, 3C, 4B
- 1A, 2B, 3C, 4D
Solución:
Comencemos por definir brevemente cada uno de los conceptos, para luego relacionarlos con sus respectivos modelos matemáticos.
Ley de corrientes de Kirchhoff.
Esta ley de los circuitos eléctricos, establece que la sumatoria de las corrientes entrantes en un nodo es igual a la sumatoria de las corrientes que salen de él.
\sum {i}_{in}=\sum {i}_{out}
1B.
Capacitores en serie.
La fórmula para calcular la capacitancia equivalente de condensadores en serie es:
C=\frac{1}{\frac{1}{{C}_{1}}+\frac{1}{{C}_{2}}+\frac{1}{{C}_{3}}+\dots }=\frac{1}{\sum \frac{1}{{C}_{i}}}
2A.
Potencia eléctrica.
Se calcula como el producto del voltaje aplicado a un dispositivo, con la corriente que le recorre.
P=V\cdot I
3C.
Resistores en paralelo.
Para calcular la resistencia equivalente de resistores conectados en paralelo, empleamos la ecuación:
R=\frac{1}{\frac{1}{{R}_{1}}+\frac{1}{{R}_{2}}+\frac{1}{{R}_{3}}+\dots }=\frac{1}{\sum \frac{1}{{R}_{i}}}
4D.
Combinando las respuestas parciales nos queda:
1B, 2A, 3C, 4D.
Comparando con los incisos, concluimos que la respuesta correcta es a).
Reactivo 36
Se tiene una onda electromagnética que se propaga en el vacío a la velocidad de la luz c=3\cdot {10}^{8} \mathrm{m}/\mathrm{s} , con una frecuencia de 100,000 Hz. Calcule la longitud de onda.
- 30 m
- 300 m
- 3000 m
- 3 m
Solución:
Para calcular la longitud de cualquier onda, empleamos la siguiente ecuación:
v=\lambda f
Donde v es la rapidez de la onda, \lambda es la longitud de onda y f es la frecuencia. Despejamos a \lambda .
\lambda =\frac{v}{f}
Sustituimos los valores.
\lambda =\frac{3\cdot {10}^{8} \mathrm{m}/\mathrm{s}}{\mathrm{100,000}\mathrm{ }\mathrm{H}\mathrm{z}}=3000 \mathrm{m}=3\mathrm{ }\mathrm{k}\mathrm{m}
La longitud de onda es igual a 3 kilómetros.
Concluimos que la respuesta correcta es el inciso b).
Reactivo 37
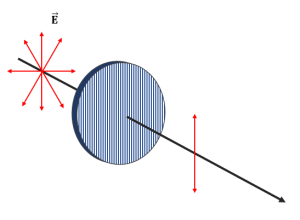
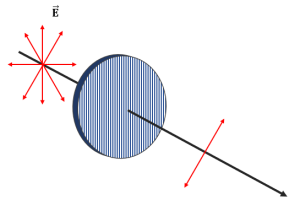
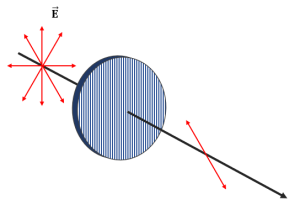
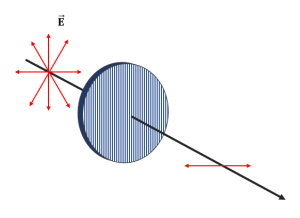
En la figura se muestra un rayo de luz no polarizada que se hace pasar a través de un polarizador por absorción cuyo eje de transmisión es el que indican las líneas sobre él. Determine cuál de las siguientes opciones corresponde a la luz transmitida por el polarizador.
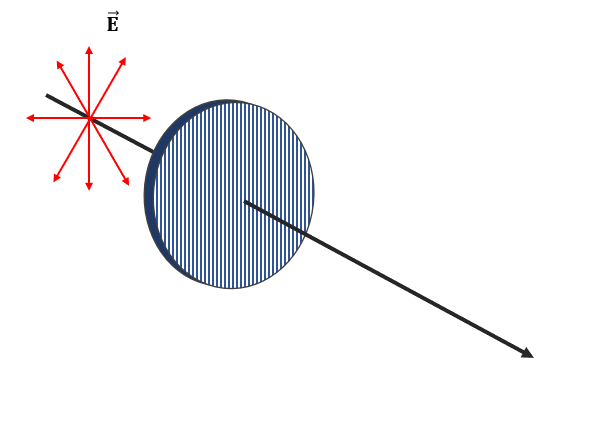
Solución:
Recordemos rápidamente los conceptos básicos sobre la polarización de la luz y, más específicamente, los polarizadores por absorción.
Se conoce como luz polarizada a todo haz cuyo campo eléctrico vibra en una misma dirección, teniendo en cuenta determinado punto del espacio. Por otra parte, la luz no polarizada se suele indicar mediante flechas que apuntan en todas las direcciones, mientras que la luz polarizada con una sola flecha que indica el sentido del campo eléctrico.

La polarización por absorción, consiste en construir una película de material con cadenas alargadas de hidrocarburos, de tal forma que cuando el campo eléctrico incide sobre ellas induciendo corrientes en las cadenas y debilitándose en el proceso. De esta forma, el campo eléctrico que vibra en esa dirección es “absorbido” y no atraviesa el material.
La dirección perpendicular a las cadenas permite el paso total del campo eléctrico que vibra en dicha dirección, por esta razón, recibe el nombre de eje de transmisión. En todo filtro polarizador por absorción, las líneas que se dibujan indican la dirección del eje de transmisión.
Ahora, debido a que el eje de transmisión del polarizador es vertical, concluimos que el campo eléctrico que vibra en dicha dirección es el transmitido. Comparando con las opciones, concluimos que la respuesta correcta es la a).
Reactivo 38
Consideremos un rayo de luz que pasa del medio 1 al medio 2, de tal forma que su ángulo de incidencia es igual a 60° y se refracta a través del medio 2 con un ángulo de 40°. Calcule el índice de refracción {n}_{2-1} .
- 1.447
- 1.347
- 1.247
- 1.147
Solución:
La ley de Snell nos dice que el cociente entre el valor del seno del ángulo de incidencia con el valor del seno del ángulo de refracción es constante y se denomina índice de refracción {n}_{I-R} .
{n}_{R-I}=\frac{\mathrm{sin}{\theta }_{I}}{\mathrm{sin}{\theta }_{R}}
Sustituimos los ángulos dados.
{n}_{2-1}=\frac{\mathrm{sin}60°}{\mathrm{sin}40°}=1.347
El índice de refracción que experimenta la luz al pasar del medio 1 al medio 2 es de 1.347 .
Concluimos indicando como respuesta correcta al inciso b).
Reactivo 39
¿Qué sucede con la velocidad de las ondas sonoras en un medio, si su densidad incrementa 4/3 respecto a la densidad original? Considere al medio como un gas ideal.
- La velocidad permanece igual
- La velocidad aumenta
- La velocidad disminuye
- La velocidad es el doble
Solución:
Recordemos que la velocidad del sonido en un medio gaseoso puede calcularse a partir de la siguiente ecuación:
v=\sqrt{\frac{\gamma P}{\rho }}
Teniendo en cuenta que solo cambia la densidad del medio, podemos indicar la velocidad según las densidades como:
{v}_{1}=\sqrt{\frac{\gamma P}{{\rho }_{1}}} y {v}_{2}=\sqrt{\frac{\gamma P}{{\rho }_{2}}}
El enunciado nos dice que la densidad {\rho }_{2} incrementa 4/3, por tanto:
{\rho }_{2}={\rho }_{1}+\frac{4}{3}{\rho }_{1}=\frac{7}{3}{\rho }_{1}
Sustituimos en la velocidad 2.
{v}_{2}=\sqrt{\frac{\gamma P}{\frac{7}{3}{\rho }_{1}}}=\sqrt{\frac{3}{7}}\cdot \sqrt{\frac{\gamma P}{{\rho }_{1}}}
Sustituyendo \sqrt{\frac{\gamma P}{{\rho }_{1}}} por {v}_{1} :
{v}_{2}=\sqrt{\frac{3}{7}} {v}_{1}=0.65465{v}_{1}
La velocidad {v}_{2} del sonido es menor respecto a {v}_{1} al aumentar la densidad del medio.
Concluimos que la respuesta correcta es el inciso c).
Reactivo 40
Un cuerpo acoplado a un resorte sube y baja verticalmente describiendo un MAS. Si la amplitud del movimiento es de 10 cm y el periodo de oscilación es igual a 1 s, calcule la velocidad cuando la posición incrementa a y=5 \mathrm{c}\mathrm{m} .
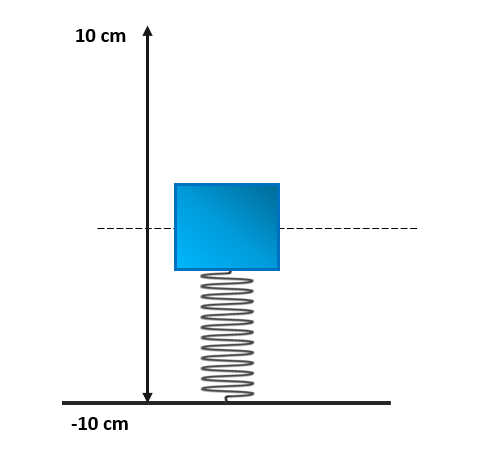
- 5.44 \mathrm{m}/\mathrm{s}
- 0.44 \mathrm{m}/\mathrm{s}
- 1.544 \mathrm{m}/\mathrm{s}
- 0.544 \mathrm{m}/\mathrm{s}
Solución:
Para resolver este problema de movimiento armónico simple, debemos recordar la ecuación para calcular la velocidad en función de la posición.
v=\pm \omega \sqrt{{a}^{2}-{y}^{2}}
Donde a es la amplitud del movimiento, y la posición y v la velocidad. Ahora, debemos saber cuándo utilizar la parte positiva y negativa de la ecuación. Empleamos la parte negativa cuando el objeto se encuentra descendiendo y positiva cuando el objeto asciende. Debido a que la masa incrementa desde 0 hasta 5 cm, empleamos la ecuación positiva. Calculamos ahora la velocidad angular.
\omega =\frac{2\pi }{\tau }=\frac{2\pi }{1 \mathrm{s}}=2\pi \mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}
Sustituimos los valores en la ecuación.
v=\left(2\pi \right)\sqrt{{0.1}^{2}-{0.05}^{2}}=0.544 \mathrm{m}/\mathrm{s}
La velocidad de la masa cuando y=0.05 \mathrm{m} es de 0.544 \mathrm{m}/\mathrm{s} .
La respuesta correcta es el inciso d).