Hola de nuevo aspirante, vamos con la tercera parte del simulacro de física del IPN para el área de Ingeniería y Ciencias Físico Matemáticas.

En esta parte del examen simulador vamos a resolver los reactivos del 21 al 30.
Reactivo 21
A partir del sistema que se muestra en la figura, determine la masa que debería tener el bloque 1 para que permanezca estable.
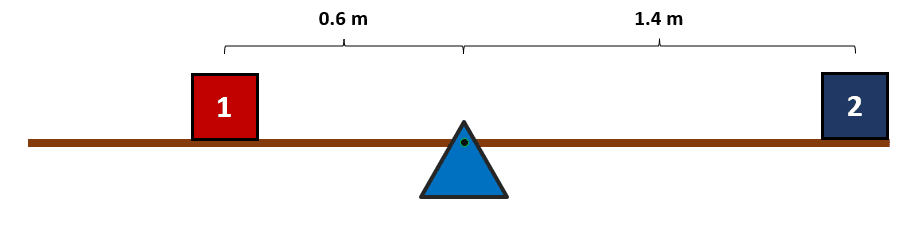
Tenga en cuenta que el bloque 2 tiene una masa de 0.8 kilogramos.
- 1.86 \mathrm{k}\mathrm{g}
- 2.86 \mathrm{k}\mathrm{g}
- 0.86 \mathrm{k}\mathrm{g}
- 0.186 \mathrm{k}\mathrm{g}
Solución:
En este problema, nos interesa que el sistema sea estable respecto a las torcas. Aplicando la segunda condición de estabilidad y asumiendo torcas positivas en sentido antihorario, obtenemos que:
\sum \tau =0\to {\tau }_{1}-{\tau }_{2}=0
{\tau }_{1}={\tau }_{2}
Recordando la definición de torca.
\tau =rF
En nuestro caso, la fuerza es el peso respectivo de cada masa.
{r}_{1}{m}_{1}g={r}_{2}{m}_{2}g
Despejamos la masa {m}_{1} .
{m}_{1}=\frac{{r}_{2}}{{r}_{1}}{m}_{2}=\frac{1.4}{0.6}\left(0.8\right)=1.86 \mathrm{k}\mathrm{g}
Para que el sistema sea estable, la masa del bloque 1 debe ser de 1.86 kilogramos.
Concluimos que la respuesta correcta es la opción a).
Reactivo 22
Se lanza una pelota de béisbol de 180 gramos en dirección totalmente horizontal hacia un bateador situado en home. La rapidez de la pelota es de 25 metros por segundo y se mantiene casi invariante hasta que entra en contacto con el bate. En este punto, la pelota es bateada de forma horizontal y con una fuerza de 500 Newtons en sentido contrario al movimiento. Si el contacto dura 0.03 segundos, calcule la velocidad con la que sale la pelota.
- 58.33\widehat{i}\frac{\mathrm{m}}{\mathrm{s}}
- 8.33\widehat{i}\frac{\mathrm{m}}{\mathrm{s}}
- -8.33\widehat{i}\frac{\mathrm{m}}{\mathrm{s}}
- -58.33\widehat{i}\frac{\mathrm{m}}{\mathrm{s}}
Solución:
A partir de los temas relacionados con la dinámica de los cuerpos, sabemos que existe una relación de igualdad entre el impulso y la variación de momento lineal que puede expresarse como:
\overrightarrow{F}\cdot \mathrm{\Delta }t=m\cdot \mathrm{\Delta }\overrightarrow{v}
El miembro de la izquierda corresponde al impulso y el de la derecha a la variación del momento lineal. Debido a que esta ecuación es vectorial, tenemos que establecer el sentido de las velocidades y la fuerza.
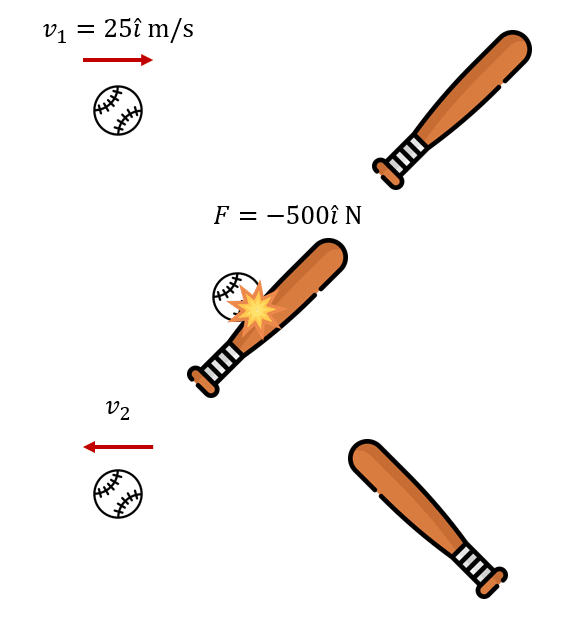
Sustituimos en la ecuación.
\left(-500\widehat{i}\right)\left(0.03 \mathrm{s}\right)=\left(0.18 \mathrm{k}\mathrm{g}\right)\left({v}_{2}-25\widehat{i}\right)
{v}_{2}=\frac{\left(-500\widehat{i}\right)\left(0.03\right)}{0.18}+25\widehat{i}=-58.33\widehat{i}\frac{\mathrm{m}}{\mathrm{s}}
La pelota de béisbol sale disparada con una velocidad de 58.33 metros por segundo en dirección -\widehat{i} .
Concluimos indicando que la respuesta correcta es el inciso d).
Reactivo 23
Si un cuerpo que tiene una masa de 250 gramos ocupa un volumen de 500 mililitros, ¿cuál es la densidad del cuerpo?
- 50\frac{\mathrm{k}\mathrm{g}}{{\mathrm{m}}^{3}}
- 5000\frac{\mathrm{k}\mathrm{g}}{{\mathrm{m}}^{3}}
- 500\frac{\mathrm{k}\mathrm{g}}{{\mathrm{m}}^{3}}
- 5500\frac{\mathrm{k}\mathrm{g}}{{\mathrm{m}}^{3}}
Solución:
Para calcular la densidad de una sustancia o cuerpo, simplemente dividimos su masa en kilogramos por el volumen que ocupa en metros cúbicos. En este caso, es necesario convertir ambas magnitudes.
Convirtiendo la masa.
250 \mathrm{g}\cdot \frac{1 \mathrm{k}\mathrm{g}}{1000 \mathrm{g}}=0.25 \mathrm{k}\mathrm{g}
Ahora el volumen.
500 \mathrm{m}\mathrm{l}\cdot \frac{1 l}{1000 \mathrm{m}\mathrm{l}}\cdot \frac{1 {\mathrm{m}}^{3}}{1000 l}=0.0005 {\mathrm{m}}^{3}
Sustituimos en la ecuación.
\rho =\frac{0.25 \mathrm{k}\mathrm{g}}{0.0005 {\mathrm{m}}^{3}}=500\frac{\mathrm{k}\mathrm{g}}{{\mathrm{m}}^{3}}
La respuesta correcta es el inciso c).
Reactivo 24
Calcule el empuje que experimenta un cuerpo que desplaza un volumen de 0.01 {\mathrm{m}}^{3} dentro de una sustancia con una densidad de 997 \mathrm{k}\mathrm{g}/{\mathrm{m}}^{3} . Considere la aceleración de la gravedad como g=10 \mathrm{m}/{\mathrm{s}}^{2} .
- 997 \mathrm{N}
- 99.7 \mathrm{N}
- 9.97 \mathrm{N}
- 1000 \mathrm{N}
Solución:
Para resolver este problema, necesitamos aplicar el principio de Arquímedes el cual nos dice que la fuerza de empuje que experimenta un cuerpo total o parcialmente sumergido, es igual a la densidad de la sustancia, por la gravedad, por el volumen desplazado.
E={\rho }_{s}g{V}_{d}
Sustituimos los datos dados por el enunciado.
E=\left(997 \mathrm{k}\mathrm{g}/{\mathrm{m}}^{3}\right)\left(10 \mathrm{m}/{\mathrm{s}}^{2}\right)\left(0.01 {\mathrm{m}}^{3}\right)=99.7 \mathrm{N}
El cuerpo experimenta un empuje de 99.7 Newtons.
La respuesta correcta es la opción b).
Reactivo 25
En la figura se muestra una configuración de 3 cargas eléctricas sobre un plano cartesiano. Si {q}_{1}=3\times {10}^{-3} \mathrm{C} , {q}_{2}=-2\times {10}^{-3} \mathrm{C} y {q}_{3}=1.5\times {10}^{-3} \mathrm{C} , calcule la fuerza resultante sobre la carga {q}_{1} .
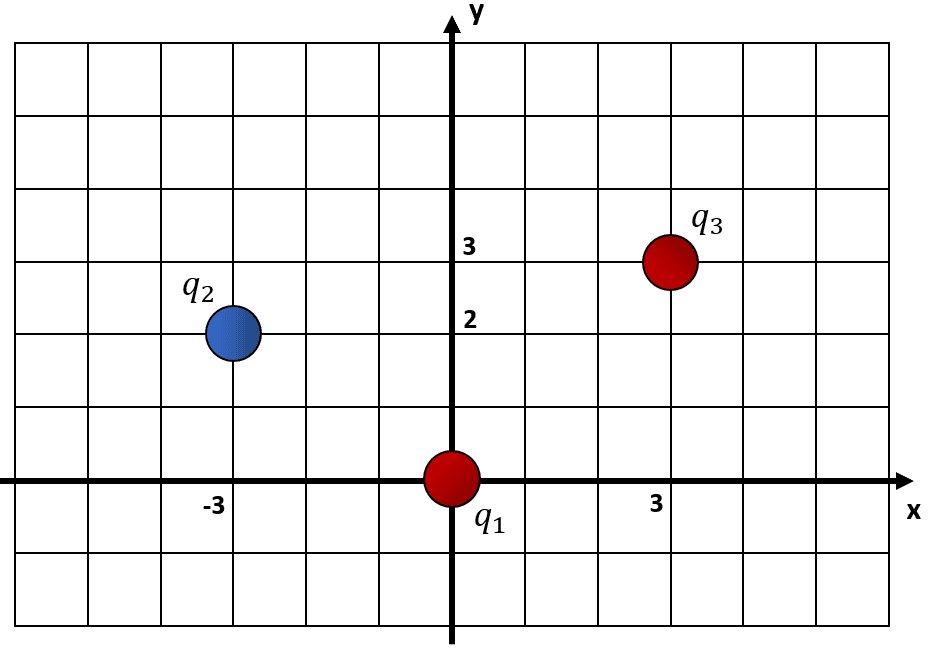
Tenga en cuenta {k}_{e}=9\times {10}^{9} \frac{\mathrm{N}\cdot {\mathrm{m}}^{2}}{{\mathrm{C}}^{2}} .
- \left(713.7\widehat{j}\right) \mathrm{N}
- \left(-5046.8\widehat{i}\right) \mathrm{N}
- \left(-5046.8\widehat{i}+713.7\widehat{j}\right) \mathrm{N}
- \left(5046.8\widehat{i}+713.7\widehat{j}\right) \mathrm{N}
Solución:
Para resolver este problema, necesitamos aplicar dos conceptos: la Ley de Coulomb y la fuerza resultante sobre un cuerpo. Examinando la figura, determinamos que la carga {q}_{1} experimenta dos fuerzas, una {F}_{12} debido a la carga 2 y otra {F}_{13} debido a la carga 3.
Recordando la naturaleza de las interacciones eléctricas, cargas opuestas se atraen y cargas iguales se repelen. Teniendo en cuenta esto, la fuerza {F}_{12} apunta en dirección a {q}_{2} y la fuerza {F}_{13} apunta en la dirección contraria a {q}_{3} .
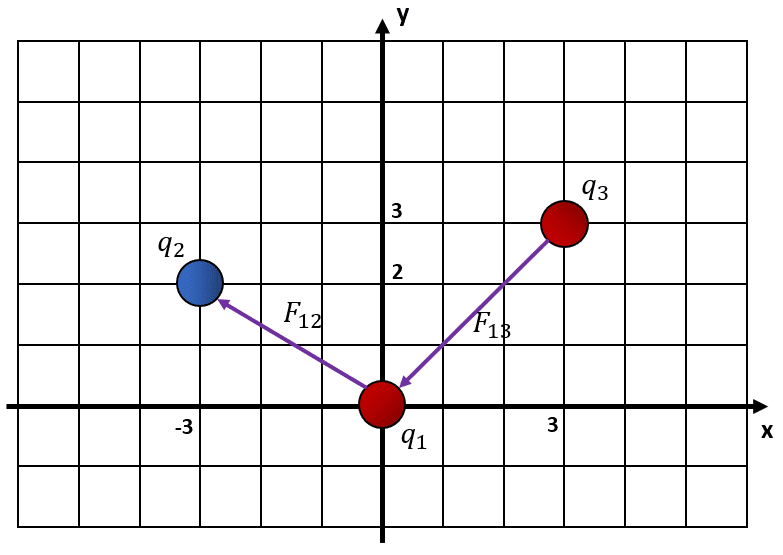
Debido a que las fuerzas no son totalmente horizontales o verticales, la forma de resolver el problema es la siguiente: calculamos el módulo de cada fuerza y luego la descomponemos en los ejes coordenados según las direcciones que hemos establecido.
Cálculo de la fuerza {F}_{12} .
{F}_{12}=\frac{{k}_{e}\left|{q}_{1}{q}_{2}\right|}{{d}_{12}^{2}}
Calculamos la distancia {d}_{12} aplicando el teorema de Pitágoras.
{d}_{12}^{2}={2}^{2}+{\left(-3\right)}^{2}=13
Sustituimos.
{F}_{12}=\frac{\left(9\times {10}^{9} \frac{\mathrm{N}\cdot {\mathrm{m}}^{2}}{{\mathrm{C}}^{2}}\right)\left|\left(3\times {10}^{-3} \mathrm{C}\right)\left(-2\times {10}^{-3} \mathrm{C}\right)\right|}{13}=4153.84 \mathrm{N}
Calculamos el ángulo que debería tener la fuerza.
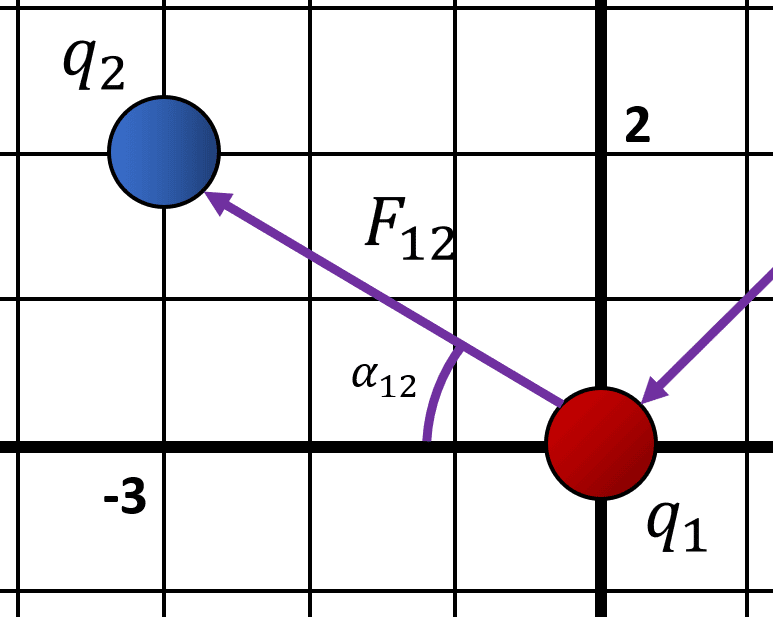
Aplicando la tangente nos queda que:
{\alpha }_{12}={\mathrm{tan}}^{-1}\left(\frac{2}{3}\right)=33.7°
Las componentes de la fuerza serían:
{F}_{12x}=-4153.84\mathrm{cos}\left(33.7°\right)=-3455.8 \mathrm{N}
{F}_{12y}=4153.84\mathrm{sin}\left(33.7°\right)=2304.7 \mathrm{N}
{F}_{12}=\left(-3455.8\widehat{i}+2304.7\widehat{j}\right)\mathrm{ }\mathrm{N}
Cálculo de la fuerza {F}_{13} .
{F}_{13}=\frac{{k}_{e}\left|{q}_{1}{q}_{3}\right|}{{d}_{13}^{2}}
{d}_{13}^{2}={3}^{2}+{3}^{2}=18
Sustituimos.
{F}_{13}=\frac{\left(9\times {10}^{9} \frac{\mathrm{N}\cdot {\mathrm{m}}^{2}}{{\mathrm{C}}^{2}}\right)\left|\left(3\times {10}^{-3} \mathrm{C}\right)\left(1.5\times {10}^{-3} \mathrm{C}\right)\right|}{18}=2250 \mathrm{N}
Calculamos el ángulo de la fuerza.
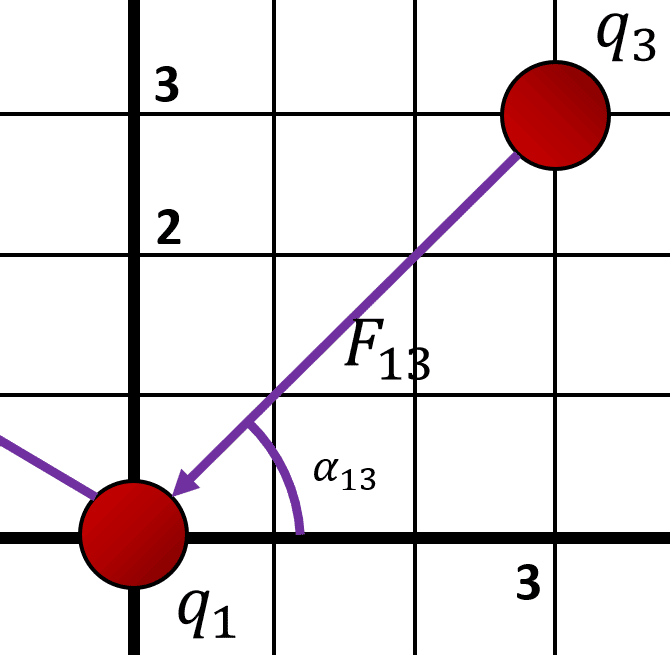
{\alpha }_{13}={\mathrm{tan}}^{-1}\left(\frac{3}{3}\right)=45°
Las componentes de la fuerza serían:
{F}_{13x}=-2250\mathrm{cos}\left(45°\right)=-1591 \mathrm{N}
{F}_{13y}=-2250\mathrm{sin}\left(45°\right)=-1591 \mathrm{N}
{F}_{13}=\left(-1591\widehat{i}-1591\widehat{j}\right)\mathrm{ }\mathrm{N}
Finalmente, aplicamos fuerza resultante.
{F}_{1}={F}_{12}+{F}_{13}=\left(-3455.8\widehat{i}+2304.7\widehat{j}\right)\mathrm{ }\mathrm{N}+\left(-1591\widehat{i}-1591\widehat{j}\right)\mathrm{ }\mathrm{N}
{F}_{1}=\left(-5046.8\widehat{i}+713.7\widehat{j}\right) \mathrm{N}
Comparando con los incisos, concluimos que la respuesta correcta es c).
Reactivo 26
Calcule la presión hidrostática que experimentaría un buzo al sumergirse 40 metros bajo el agua. Tenga en cuenta que la densidad de la sustancia es de 1023 \mathrm{k}\mathrm{g}/{\mathrm{m}}^{3} y considere la aceleración de la gravedad 10 \mathrm{m}/{\mathrm{s}}^{2} .
- 409 \mathrm{P}\mathrm{a}
- 4092 \mathrm{P}\mathrm{a}
- 40920 \mathrm{P}\mathrm{a}
- 409200 \mathrm{P}\mathrm{a}
Solución:
Para resolver este problema, debemos emplear la ecuación de presión hidrostática en el interior de un fluido en equilibrio.
P=\rho \cdot g\cdot h
Sustituimos directamente los datos suministrados por el enunciado.
P=\left(1023 \mathrm{k}\mathrm{g}/{\mathrm{m}}^{3}\right)\left(10 \mathrm{m}/{\mathrm{s}}^{2}\right)\left(40 \mathrm{m}\right)=409200 \mathrm{P}\mathrm{a}
El buzo experimentaría una presión de 409200 Pascales.
Concluimos indicando como respuesta correcta el inciso d).
Reactivo 27
Se tiene encerrado un gas considerado ideal en un recinto que tiene conectado un termómetro y un manómetro. Si la sustancia se expone a un proceso isométrico, en el que su temperatura se lleva de 23 °C a 150 °C, calcule la presión al final del proceso teniendo en cuenta que inicialmente era de 120 kPa.
- 161.46 \mathrm{k}\mathrm{P}\mathrm{a}
- 171.46 \mathrm{k}\mathrm{P}\mathrm{a}
- 181.46 \mathrm{k}\mathrm{P}\mathrm{a}
- 191.46 \mathrm{k}\mathrm{P}\mathrm{a}
Solución:
Para resolver este problema, debemos aplicar la ley de los gases ideales en procesos isométricos, es decir, en procesos con volumen constante.
\frac{{P}_{1}}{{T}_{1}}=\frac{{P}_{2}}{{T}_{2}}
Antes de sustituir, debemos convertir las temperaturas de °C a Kelvin.
{T}_{1}=23+273.15=296.15 \mathrm{K}
{T}_{2}=150+273.15=423.15 \mathrm{K}
La presión en el primer instante ya se encuentra en pascales, por tanto, solo nos queda sustituir.
{P}_{2}=\frac{{T}_{2}}{{T}_{1}}{P}_{1}=\frac{423.15 \mathrm{K}}{296.15 \mathrm{K}}\left(120 \mathrm{k}\mathrm{P}\mathrm{a}\right)=171.46 \mathrm{k}\mathrm{P}\mathrm{a}
La presión al final del proceso es de 171.46 kPa o 171460 Pa.
Concluimos que la respuesta correcta es el inciso b).
Reactivo 28
Calcule el trabajo que realiza un gas a presión constante de 220 \mathrm{k}\mathrm{P}\mathrm{a} , cuando luego de ser calentado se expande 0.012 metros cúbicos.
- 6400 \mathrm{J}
- 640 \mathrm{J}
- 1640 \mathrm{J}
- 2640 \mathrm{J}
Solución:
Para calcular el trabajo realizado por un gas durante un proceso isobárico, empleamos la siguiente ecuación.
W=P\left({V}_{2}-{V}_{1}\right)
Donde P es la presión del gas y {V}_{2}-{V}_{1} corresponde a la variación de volumen entre el estado 1 y el estado 2. El enunciado no nos indica el volumen en cada estado, pero si la expansión, es decir, la diferencia directamente.
{V}_{2}-{V}_{1}=0.012 {\mathrm{m}}^{3}
Sustituimos en la ecuación recordemos que kPa equivale a 1000 Pa.
W=\left(220 \mathrm{k}\mathrm{P}\mathrm{a}\right)\left(0.012 {\mathrm{m}}^{3}\right)=\left(220000 \mathrm{P}\mathrm{a}\right)\left(0.012 {\mathrm{m}}^{3}\right)=2640 \mathrm{J}
El gas produce 2640 Joules de trabajo durante todo el proceso.
La respuesta correcta se encuentra en el inciso d).
Reactivo 29
Se coloca una carga de prueba en las inmediaciones de un campo eléctrico estacionario. Si la carga es de 1\times {10}^{-3} \mathrm{C} y experimenta una fuerza de 20 N en ese punto, ¿cuál es la magnitud del campo eléctrico?
- 200000 \mathrm{N}/\mathrm{C}
- 20000 \mathrm{N}/\mathrm{C}
- 2000 \mathrm{N}/\mathrm{C}
- 200 \mathrm{N}/\mathrm{C}
Solución:
Para calcular el campo eléctrico en cualquier punto del espacio, empleamos la siguiente ecuación:
E=\frac{F}{{q}_{o}}
Donde {q}_{o} es la carga eléctrica de prueba. Sustituimos los valores dados por el problema.
E=\frac{20 \mathrm{N}}{1\times {10}^{-3} \mathrm{C}}=20000 \mathrm{N}/\mathrm{C}
El campo eléctrico en dicho punto tiene una intensidad de 20000 \mathrm{N}/\mathrm{C} .
Comparando con las opciones, concluimos que la respuesta correcta está en la b).
Reactivo 30
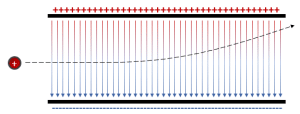
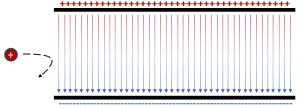
Se tiene una partícula que se desplaza uniformemente al encontrarse con un campo eléctrico perpendicular a su dirección de movimiento, tal como se muestra en la figura.
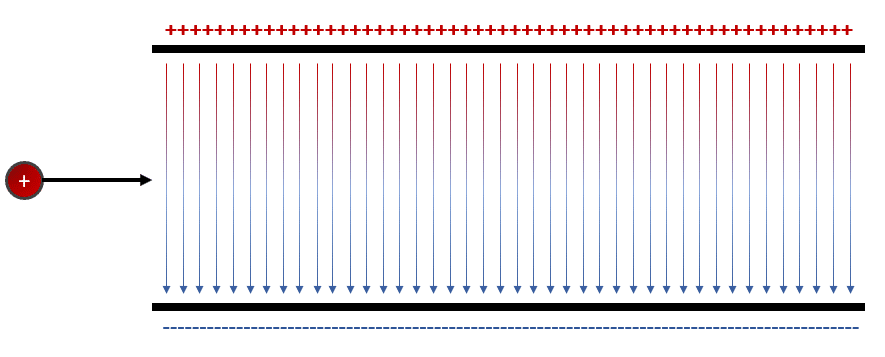
Determine cuál de las siguientes opciones describe correctamente la trayectoria que seguiría la partícula.
Solución:
Para responder a esta pregunta, recordemos cómo interactúan las cargas eléctricas con los campos eléctricos. Las líneas de campo de una carga positiva salen de ella, mientras que, para las cargas negativas las líneas de campo son entrantes.
En esta línea de ideas, una carga positiva sentirá una fuerza de atracción en la misma dirección del campo eléctrico, mientras que una carga negativa sentirá una fuerza en sentido contrario a la dirección del campo eléctrico.
Llevando estas ideas a la situación planteada en el enunciado, la carga no experimenta ninguna fuerza en la dirección del movimiento, por tanto, mantiene invariante su desplazamiento horizontal.
Por otra parte, al ser una carga positiva sentirá una fuerza que tira de ella hacia abajo y, por ende, una aceleración vertical y hacia abajo.
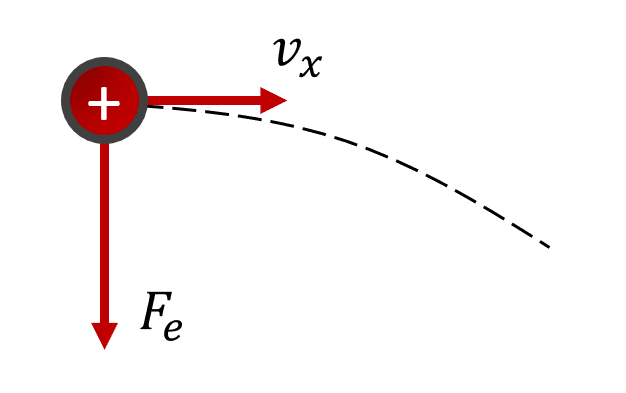
Examinando los incisos, concluimos que la respuesta correcta es c).