¡Hola aspirante al IPN! En este simulador de examen vamos a resolver 50 ejercicios de física con los temas oficiales de la guía del IPN para carreras del área de Ciencias Sociales y Administrativas.
Vamos a dividirlo en 5 partes para que vayas resolviéndolos poco a poco.

Acá tienes un resumen con lo más importante del examen de ingreso al IPN:
- Carreras ofertadas en IPN: 70+
- Porcentaje de aceptación: 20%
- Preguntas en el examen de admisión: 140 preguntas
- Nuevos temas: Historia e Inglés (reading comprehension)
- Tipo: selección múltiple
Recuerda estudiar bien los conceptos físicos y resolver los reactivos por tu cuenta antes de mirar la solución.
Estructura Examen IPN
El examen para ingresar al Politécnico Nacional está dividido en dos bloques: conocimientos generales y conocimientos experimentales. Sin embargo, este año se han realizado algunos cambios que debes tener en cuenta para iniciar tu preparación:
- El examen evaluará la materia de inglés, específicamente en el tema de Reading comprehension.
- Las materias de competencia escrita y competencia lectora, sustituyeron a producción escrita y comprensión de textos.
- Cada área asigna la cantidad de reactivos por materia (puedes consultar los reactivos en la tabla que te dejamos más adelante).
- Se agregó la materia de historia de México a las tres áreas de estudio.
- El examen para todas las carreras tendrá 140 reactivos (anteriormente eran 130).
La dificultad de los bloques varía según la carrera a la que desees ingresar, puedes consultar la lista de carreras ofertadas por el IPN en el siguiente enlace.
La siguiente tabla muestra la estructura de reactivos por materia para cada área:
| Materia | IyCFM | CMB | CSyA |
|---|---|---|---|
| Matemáticas | 37 | 33 | 35 |
| Competencia escrita | 20 | 20 | 25 |
| Competencia lectora | 20 | 20 | 20 |
| Reading comprehension | 10 | 10 | 10 |
| Historia | 10 | 10 | 20 |
| Biología | 9 | 17 | 10 |
| Química | 17 | 17 | 10 |
| Física | 17 | 13 | 10 |
Temario de Física
Los temas para el área de Física abarcan todo el contenido que se dicta en los cursos de bachillerato, con mayor o menor énfasis en ciertos temas según el área a la que pertenezca tu carrera.
Este es el temario de física por área:
| Tema | Rama |
|---|---|
| Sistemas de unidades y mediciones | IyCFM, CMB |
| Introducción a la física | CSyA |
| Álgebra vectorial | IyCFM, CMB |
| Cinemática | IyCFM, CSyA |
| Estática | IyCFM, CMB, CSyA |
| Cinemática y dinámica | CMB |
| Leyes de newton | IyCFM |
| Dinámica | CSyA |
| Propiedades generales de la materia | CMB |
| Propiedades de la materia | IyCFM, CSyA |
| Mecánica de fluidos | CMB |
| Calor y temperatura | CSyA |
| Termodinámica | IyCFM, CMB |
| Electricidad y magnetismo | CSyA |
| Electroestática | IyCFM |
| Acústica | CMB |
| Electrodinámica | IyCFM |
| Electricidad | CMB |
| Celdas electroquímicas | IyCFM |
| Electromagnetismo | IyCFM, CMB |
| Ondas | IyCFM, CSyA |
| Electroinducción-Ondas electromagnéticas | CMB |
| Óptica | CMB |
Estos son los temas que vamos a abarcar en este examen simulacro:
- Introducción a la física.
- Cinemática.
- Estática.
- Dinámica.
- Propiedades de la materia.
- Calor y temperatura.
- Electricidad y magnetismo.
- Ondas.
¿Cómo resolver el simulacro?
Estos problemas han sido diseñados para que puedas practicar los temas del examen real y mejorar el tiempo que tardas en resolverlos.
Incluye exámenes simulacro en tu rutina de estudio, de esa forma pondrás a prueba tus conocimientos en condiciones similares a la prueba real.
Las siguientes son sugerencias para tener en cuenta mientras estudias con este simulacro.
- Resuelve cada parte (I, II y III) por tu cuenta antes de checar las respuestas.
- Establece un tiempo no mayor a 15 minutos por cada 10 reactivos.
- Analiza el procedimiento al resolver los ejercicios y piensa en posibles alternativas que mejoren tu tiempo.
- Asegúrate de tener unos minutos de sobra para comprobar tus respuestas.
- Si un ejercicio parece complejo, ve al siguiente y resuélvelo de último. Lo mejor es mantener la concentración y no entrar en pánico.
Reactivo 1
Escribe en notación científica la medida 0.00025 \mathrm{k}\mathrm{g} .
- 250\cdot {10}^{-5} \mathrm{k}\mathrm{g}
- 25\cdot {10}^{-6} \mathrm{k}\mathrm{g}
- 2.5\cdot {10}^{-4} \mathrm{k}\mathrm{g}
- 250\cdot {10}^{-6} \mathrm{k}\mathrm{g}
Solución:
La notación científica permite expresar números muy grandes o muy pequeños como potencias de base 10. Para los números grandes el exponente es positivo y para los números pequeños el exponente es negativo.
Al convertir un número a notación científica debemos seguir las siguientes reglas:
- El primer factor debe ser un número comprendido entre 1 y 10.
- El segundo factor es una potencia de base 10 que tiene como exponente un número positivo o negativo que indica las veces que la coma se movió hacia la izquierda o hacia la derecha, respectivamente.
Teniendo todo esto en cuenta, para transformar el 0.00025 \mathrm{k}\mathrm{g} a notación científica debemos correr la coma hacia la derecha hasta llegar a un número entre 1 y 10, el exponente corresponderá a la cantidad de espacios recorridos y tendrá signo negativo.
0.00025 \mathrm{k}\mathrm{g}=2.5\cdot {10}^{-4} \mathrm{k}\mathrm{g}
Concluimos finalmente que la respuesta correcta es el inciso c).
Reactivo 2
Al realizar un experimento para determinar de forma empírica una relación entre la posición de un cuerpo y que se deja caer desde una altura inicial de 1 metro, con respecto al tiempo t . Luego de analizar los datos, se ha obtenido la siguiente expresión:
y=1-4.678{t}^{2}
Encuentre la expresión del tiempo en función de la altura.
- t=-\sqrt{\frac{1-y}{4.678}}
- t=\sqrt{\frac{1-y}{4.678}}
- t=\sqrt{\frac{y-1}{4.678}}
- t=-\sqrt{\frac{y-1}{4.678}}
Solución:
Para resolver este ejercicio, simplemente debemos despejar a la variable t de la expresión dada. Comenzamos por pasar al término con t al primer miembro y la y al segundo miembro.
y=1-4.678{t}^{2}\to 4.678{t}^{2}=1-y
Ahora pasamos a dividir el 4.678.
{t}^{2}=\frac{1-y}{4.678}
Aplicamos raíz cuadrada en ambos lados.
t=\pm \sqrt{\frac{1-y}{4.678}}
En este caso nos quedamos solo con la parte positiva, porque el tiempo es siempre positivo.
t=\sqrt{\frac{1-y}{4.678}}
Concluimos que la respuesta correcta es el inciso b).
Conoce todo sobre el siguiente proceso de selección: Convocatoria IPN 2023.
Reactivo 3
Efectúe la siguiente operación y exprese el resultado en notación científica, de ser posible.
\frac{0.002\left(1000-400\right)}{0.63}
- 1.905
- 1.905\cdot {10}^{0}
- 19.05\cdot {10}^{-1}
- 1.905\cdot {10}^{1}
Solución:
Para simplificar las operaciones y obtener un resultado directamente expresado en notación científica, vamos a reescribir todas las cantidades en notación científica de tal forma que todas tengan el mismo exponente.
Comenzamos por reescribir al 0.002.
\frac{0.002\left(1000-400\right)}{0.63}=\frac{2\cdot {10}^{-3}\left(1000-400\right)}{0.63}
Escribimos al resto de cantidades en notación científica, pero con exponente positivo o negativo 3.
\frac{2\cdot {10}^{-3}\left(1000-400\right)}{0.63}=\frac{2\cdot {10}^{-3}\left(1\cdot {10}^{3}-0.4\cdot {10}^{3}\right)}{630\cdot {10}^{-3}}
Cancelamos los {10}^{-3} en el numerador con el denominador.
\frac{2\cdot {10}^{-3}\left(1\cdot {10}^{3}-0.4\cdot {10}^{3}\right)}{630\cdot {10}^{-3}}=\frac{2\left(1\cdot {10}^{3}-0.4\cdot {10}^{3}\right)}{630}
Restamos 1 con 0.4 de forma directa, porque ambos tienen potencia de base 10 con el mismo exponente.
\frac{2\left(1\cdot {10}^{3}-0.4\cdot {10}^{3}\right)}{630}=\frac{2\left(0.6\cdot {10}^{3}\right)}{630}
Multiplicamos el 2 por el 0.6.
\frac{2\left(0.6\cdot {10}^{3}\right)}{630}=\frac{1.2\cdot {10}^{3}}{630}
Resolvemos al 1.2\cdot {10}^{3} y luego efectuamos la división.
\frac{1.2\cdot {10}^{3}}{630}=\frac{1200}{630}=\frac{120}{63}=1.905
El resultado de la operación es 1.905 y no es necesario expresarlo en notación científica.
Concluimos que la respuesta correcta es el inciso a).
Reactivo 4
Dada le expresión Z=\frac{{R}^{2}+K}{1-R} , encuentra el o los valores de R que satisfacen la igualdad, si sabemos que K=98 y Z=-22 .
- R=12
- R=10
- R=-12, R=-10
- R=12, R=10
Solución:
Comenzamos despejando a R de la igualdad.
Z\left(1-R\right)={R}^{2}+K
Deshacemos la distributiva.
Z-ZR={R}^{2}+K
Reordenamos la ecuación.
{R}^{2}+ZR+K-Z=0
Sustituimos los valores de Z y R dados.
{R}^{2}-22R+98+22=0\to {R}^{2}-22R+120=0
Debido al tipo de ecuación que tenemos, sabemos que los posibles resultados de R son: ninguno, raíces repetidas o raíces distintas. Aplicamos la ecuación de segundo grado.
R=\frac{22\pm \sqrt{{\left(-22\right)}^{2}-4\left(1\right)\left(120\right)}}{2\left(1\right)}=\frac{22\pm \sqrt{4}}{2}=\frac{22\pm 2}{2}
{R}_{1}=\frac{22+2}{2}=\frac{24}{2}=12
{R}_{2}=\frac{22-2}{2}=\frac{20}{2}=10
Los valores de R que satisfacen la igualdad son 12 y 10.
La respuesta correcta es el inciso d).
Reactivo 5
Relacione las ramas de la física clásica que se enumeran en la columna izquierda, con las definiciones en la columna derecha.

- 1C, 2D, 3A, 4B
- 1C, 2B, 3D, 4A
- 1C, 2D, 3B, 4A
- 1A, 2D, 3B, 4C
Solución:
Para encontrar la combinación correcta y responder este problema, debemos valernos de las definiciones básicas sobre qué es la física y sus ramas. La física es una ciencia que estudia las propiedades de la materia y sus interacciones para entender el funcionamiento de nuestro universo a todas las escalas.
Evidentemente, una definición tan amplia implica que la física se divide en determinadas ramas y, principalmente, reconocemos dos grandes divisiones: física clásica y física moderna. En este caso, nos interesan las ramas de la física clásica.
- La mecánica estudia al movimiento y las causas que lo provocan.
- La termodinámica estudia el intercambio de calor y energía entre sistemas físicos.
- El electromagnetismo estudia las interacciones entre la materia cargada a través de la electricidad y el magnetismo.
- La óptica estudia la naturaleza e interacción de la luz.
- La acústica estudia las ondas sonoras y sus propiedades.
Teniendo en cuenta lo anterior, podemos concluir el pareo de la siguiente forma:
1C, 2D, 3B y 4A.
Comparando con las opciones, indicamos como correcta la c).
Reactivo 6
Se denomina unidad derivada a aquellas que…
- Se descubren a partir de fenómenos naturales
- No dependen de ninguna magnitud
- Son adimensionales
- Provienen de la combinación de las unidades fundamentales
Solución:
Las unidades de medida son patrones asociados a determinada magnitud física como la masa, la longitud o el tiempo, que, mediante la comparación de la magnitud respecto a esta unidad, es posible asociar una cantidad numérica al fenómeno que presenciamos.
Ahora, las unidades de medida se clasifican principalmente en dos grupos: fundamentales y derivadas. Las unidades fundamentales son aquellas seleccionadas como la base del sistema de unidades, a partir de ellas se construye el resto de unidades.
Por otra parte, las unidades derivadas se forman a partir de las fundamentales como consecuencia de observar otros fenómenos en la naturaleza que se pueden estimar de forma indirecta mediante experimentos o modelos matemáticos.
Teniendo en cuenta todo lo anterior, concluimos que el inciso que completa la frase es el d).
Se denomina unidad derivada a aquellas que provienen de la combinación de las unidades fundamentales.
Reactivo 7
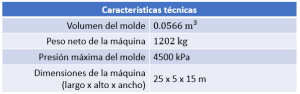
Una unidad de ingeniería que trabaja para determinada empresa, ha recibido las características técnicas de una maquinaria que necesitan para producir piezas de plástico por inyección.

Pero estas unidades no corresponden al SIU, por tanto, se le ha encomendado a usted expresar la tabla en: {\mathrm{m}}^{3} , kg, kPa y m.
Solución:
Resolver este problema será sencillo, simplemente debemos convertir cada una de las unidades indicadas en la tabla al sistema internacional. Primero, recordemos las relaciones entre cada unidad correspondiente:
1 \mathrm{m}=1.09361\mathrm{ }\mathrm{y}\mathrm{d}
1 {\mathrm{m}}^{3}=35.3147 {\mathrm{f}\mathrm{t}}^{3}
1 \mathrm{k}\mathrm{g}=2.20462\mathrm{ }\mathrm{l}\mathrm{b}
1 \mathrm{k}\mathrm{P}\mathrm{a}=0.01\mathrm{ }\mathrm{b}\mathrm{a}\mathrm{r}
Comenzamos transformando el volumen del molde.
2 {\mathrm{f}\mathrm{t}}^{3}\cdot \frac{1 {\mathrm{m}}^{3}}{35.3147 {\mathrm{f}\mathrm{t}}^{3}}=0.0566 {\mathrm{m}}^{3}
Peso de la máquina.
265 \mathrm{l}\mathrm{b}\cdot \frac{1 \mathrm{k}\mathrm{g}}{2.20462\mathrm{ }\mathrm{l}\mathrm{b}}=120.2 \mathrm{k}\mathrm{g}
Presión máxima del molde.
4.5 \mathrm{b}\mathrm{a}\mathrm{r}\cdot \frac{1 \mathrm{k}\mathrm{P}\mathrm{a}}{0.01\mathrm{ }\mathrm{b}\mathrm{a}\mathrm{r}}=450 \mathrm{k}\mathrm{P}\mathrm{a}
Dimensiones de la máquina.
\mathrm{L}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{o}=2.73\mathrm{ }\mathrm{y}\mathrm{d}\cdot \frac{1 \mathrm{m}}{1.09361\mathrm{ }\mathrm{y}\mathrm{d}}=2.5 \mathrm{m}
\mathrm{A}\mathrm{l}\mathrm{t}\mathrm{o}=5.46\mathrm{ }\mathrm{y}\mathrm{d}\cdot \frac{1 \mathrm{m}}{1.09361\mathrm{ }\mathrm{y}\mathrm{d}}=5 \mathrm{m}
\mathrm{A}\mathrm{n}\mathrm{c}\mathrm{h}\mathrm{o}=1.64\mathrm{ }\mathrm{y}\mathrm{d}\cdot \frac{1 \mathrm{m}}{1.09361\mathrm{ }\mathrm{y}\mathrm{d}}=1.5 \mathrm{m}
Sustituyendo los resultados en la tabla:

La respuesta correcta es el inciso b).
Reactivo 8
Relacione las magnitudes físicas en la columna izquierda con el tipo que se indica en la columna izquierda.

- 12A, 34B
- 14A, 23B
- 24A, 13B
- 34A, 12B
Solución:
Cuando estudiamos la naturaleza de los fenómenos que ocurren en nuestro universo, encontramos que las unidades de medida son necesarias para indicar cuánto de una magnitud estamos midiendo, pero esto no es suficiente.
Cantidades como la temperatura, el volumen o la masa pueden expresarse a través de escalares, porque solo nos interesa cuanta temperatura hay, cuanto volumen hay o cuánta masa hay, pero, ¿qué sucede con aquellos fenómenos en los que existe una dirección y un sentido?
En estos casos, es necesario el uso de vectores. La fuerza, el campo eléctrico, la presión y muchas otras magnitudes físicas contemplan como parte de su información para ser descritas matemáticamente intensidad, dirección y sentido.
Con todo lo descrito hasta este momento, podemos concluir que:
14A, 23B.
Comparando con los incisos, indicamos como correcto al b).
Reactivo 9
A partir del vector representado en la figura, identifique: inicio, extremo y magnitud.
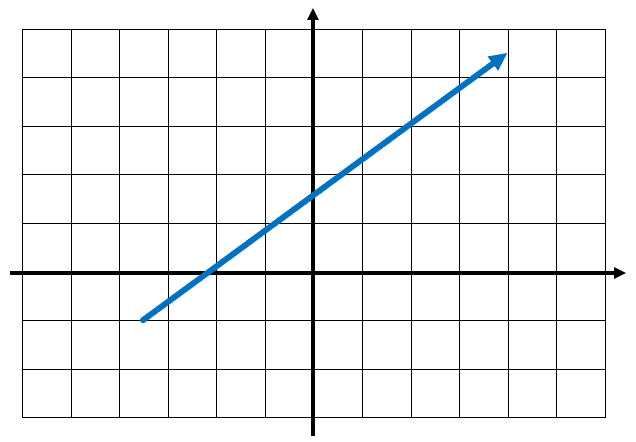
Tenga en cuenta que cada cuadrado mide 1 unidad por cada lado.
- {P}_{e}=\left(4, 4.5\right), {P}_{i}=\left(-1, -3.5\right), \left|\overrightarrow{A}\right|=9.43
- {P}_{e}=\left(4, -4.5\right), {P}_{i}=\left(-1, -3.5\right), \left|\overrightarrow{A}\right|=9.43
- {P}_{e}=\left(4, 4.5\right), {P}_{i}=\left(1, 3.5\right), \left|\overrightarrow{A}\right|=9.43
- {P}_{e}=\left(-4, -4.5\right), {P}_{i}=\left(1, 3.5\right), \left|\overrightarrow{A}\right|=9.43
Solución:
Recordemos la definición de cada uno de los elementos de los vectores que nos solicita el enunciado.
Extremo: es el punto final del vector y es hacia donde apunta la flecha.
Inicio: es el punto inicial del vector y corresponde al extremo opuesto al que apunta la flecha.
Módulo o magnitud: es la longitud o distancia representada por el vector. Se calcula como:
\left|\overrightarrow{A}\right|=\sqrt{{a}_{x}^{2}+{a}_{y}^{2}}
Para obtener las coordenadas de los extremos del vector, comenzamos por identificar su posición en los ejes coordenados.
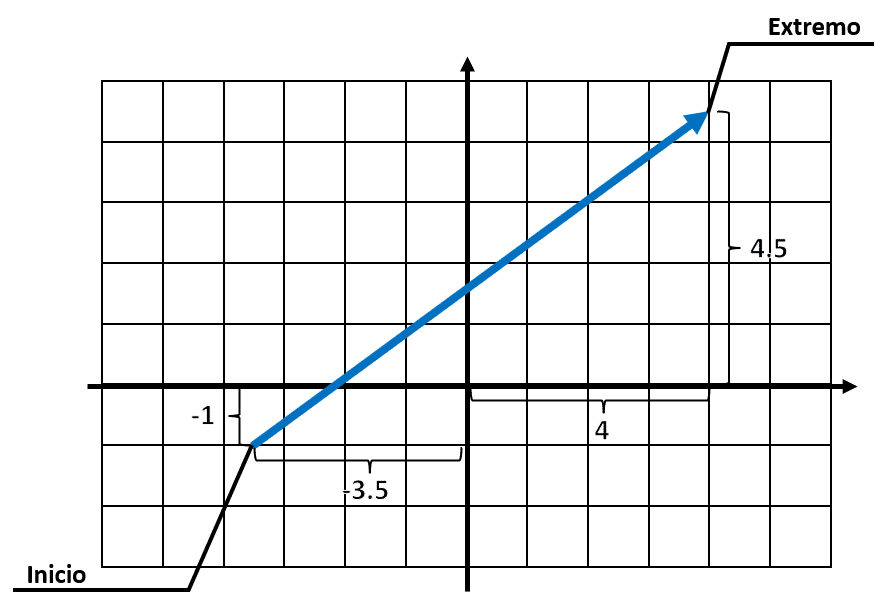
{P}_{e}=\left(4, 4.5\right), {P}_{i}=\left(-1, -3.5\right)
Calculamos la longitud del vector como:
\left|\overrightarrow{A}\right|=\sqrt{{\left(4+1\right)}^{2}+{\left(4.5+3.5\right)}^{2}}=\sqrt{{5}^{2}+{8}^{2}}=\sqrt{{5}^{2}+{8}^{2}}\approx 9.43
Finalmente:
{P}_{e}=\left(4, 4.5\right), {P}_{i}=\left(-1, -3.5\right), \left|\overrightarrow{A}\right|=9.43
Concluimos indicando como respuesta correcta la opción a).
Reactivo 10
Dados los vectores \overrightarrow{u}=\left(2, 4, -1\right) y \overrightarrow{v}=\left(1, -2, 5\right) , determine el coseno del ángulo entre ellos.
- \mathrm{cos}\theta =\frac{1}{\sqrt{630}}
- \mathrm{cos}\theta =\frac{-1}{\sqrt{630}}
- \mathrm{cos}\theta =\frac{-11}{\sqrt{630}}
- \mathrm{cos}\theta =\frac{11}{\sqrt{630}}
Solución:
Tenemos varias alternativas para el cálculo del coseno del ángulo entre dos vectores, pero en este caso, debido a que son vectores en el espacio, la mejor alternativa es emplear la definición de producto escalar.
\overrightarrow{u}\cdot \overrightarrow{v}=\left|\overrightarrow{u}\right|\left|\overrightarrow{v}\right|\mathrm{cos}\theta
Despejando nos queda:
\mathrm{cos}\theta =\frac{\overrightarrow{u}\cdot \overrightarrow{v}}{\left|\overrightarrow{u}\right|\left|\overrightarrow{v}\right|}
Ahora solo nos queda encontrar el módulo de cada vector y su producto escalar, comencemos por los módulos.
\left|\overrightarrow{u}\right|=\sqrt{{2}^{2}+{4}^{2}+{\left(-1\right)}^{2}}=\sqrt{21}
\left|\overrightarrow{v}\right|=\sqrt{{1}^{2}+{\left(-2\right)}^{2}+{5}^{2}}=\sqrt{30}
Calculamos el producto escalar.
\overrightarrow{u}\cdot \overrightarrow{v}=\left(2, 4, -1\right)\cdot \left(1, -2, 5\right)=2\cdot 1-4\cdot 2-1\cdot 5=-11
Finalmente:
\mathrm{cos}\theta =\frac{-11}{\sqrt{630}}\approx -0.43825
Comparando con los incisos, concluimos que la respuesta correcta es el c).