Seguimos con la segunda parte de la solución del examen simulador de física del área de ciencias sociales y administrativas para el examen de admisión al IPN, ahora vamos a resolver los ejercicios del 11 al 20.

Reactivo 11
Un móvil que se desplaza a una velocidad constante de 25 \mathrm{k}\mathrm{m}/\mathrm{h} acelera en determinado momento hasta obtener una velocidad final de 4 5 \mathrm{k}\mathrm{m}/\mathrm{h} , intervalo en el que recorre 100 metros. Calcule la aceleración del vehículo.
- 0.54 \mathrm{m}/{\mathrm{s}}^{2}
- 5.4 \mathrm{m}/{\mathrm{s}}^{2}
- -0.54 \mathrm{m}/{\mathrm{s}}^{2}
- -5.4 \mathrm{m}/{\mathrm{s}}^{2}
Solución:
Para comenzar el análisis de problemas de cinemática, lo más recomendable es realizar una gráfica que muestre los intervalos de movimiento con su aceleración, velocidad inicial y final junto a la distancia recorrida.
En este caso, solo tenemos a las velocidades y la distancia recorrida, la gráfica quedaría como:
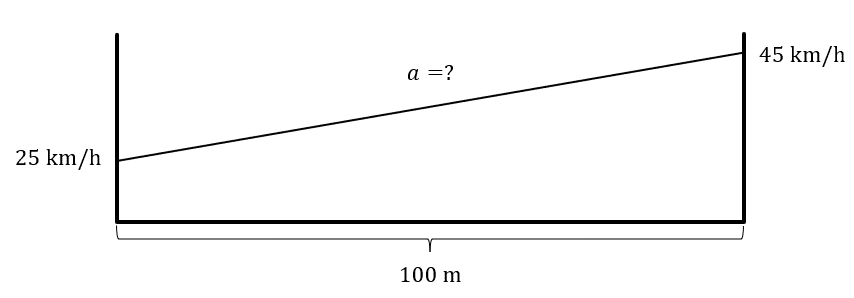
Examinando las ecuaciones de cinemática, esta es la que necesitamos en este caso:
{v}_{f}^{2}={v}_{o}^{2}+2a\mathrm{\Delta }x
Antes de despejar y sustituir los valores en la ecuación, debemos transformar las velocidades a m/s.
25\frac{\mathrm{k}\mathrm{m}}{\mathrm{h}}\cdot \frac{1000 \mathrm{m}}{1\mathrm{ }\mathrm{k}\mathrm{m}}\cdot \frac{1 \mathrm{h}}{3600 \mathrm{s}}=6.94 \mathrm{m}/\mathrm{s}
45\frac{\mathrm{k}\mathrm{m}}{\mathrm{h}}\cdot \frac{1000 \mathrm{m}}{1\mathrm{ }\mathrm{k}\mathrm{m}}\cdot \frac{1 \mathrm{h}}{3600 \mathrm{s}}=12.5 \mathrm{m}/\mathrm{s}
Despejamos la aceleración de la expresión.
{v}_{f}^{2}-{v}_{o}^{2}=2a\mathrm{\Delta }x\to \frac{{v}_{f}^{2}-{v}_{o}^{2}}{2\mathrm{\Delta }x}=a
a=\frac{{v}_{f}^{2}-{v}_{o}^{2}}{2\mathrm{\Delta }x}
Sustituimos.
a=\frac{{\left(12.5\frac{\mathrm{m}}{\mathrm{s}}\right)}^{2}-{\left(6.94\frac{\mathrm{m}}{\mathrm{s}}\right)}^{2}}{2\left(100 \mathrm{m}\right)}=0.54 \mathrm{m}/{\mathrm{s}}^{2}
La aceleración del móvil es de 0.54 \mathrm{m}/{\mathrm{s}}^{2} .
La respuesta correcta es el inciso a).
Reactivo 12
A partir del sistema que se muestra en la figura, calcule la magnitud de la tensión en la cuerda 2.
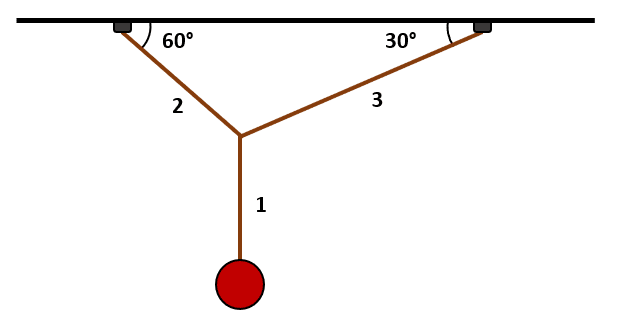
Tenga en cuenta la masa de la bola igual a 500 gramos y la aceleración de la gravedad 10 \mathrm{m}/{\mathrm{s}}^{2} .
- 0.288 N
- 2.88 N
- 28.8 N
- 288 N
Solución:
Para resolver cualquier problema de estática, debemos identificar el tipo de sistema que tenemos presente y sus partes, para establecer las condiciones de estabilidad que debemos utilizar.
El sistema consta de una masa que cuelga de una cuerda totalmente vertical, sujeta a otras dos que se encuentran atadas de tal forma que han quedado de forma oblicua.
No hay pivotes en los que puedan ocurrir rotaciones, por lo que descartamos la estabilidad debido a torcas, por lo que solo vamos a utilizar la primera ley de Newton.
Con todo esto establecido, comenzamos por dibujar el diagrama de cuerpo libre para la masa.
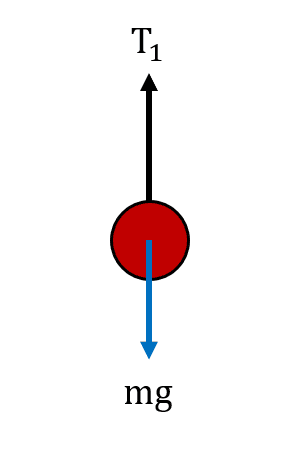
Sobre el cuerpo se manifiesta el peso y la fuerza de tensión debido a la cuerda 1.
\sum {F}_{y}=0\to {T}_{1}-mg=0
Despejamos la tensión {T}_{1} .
{T}_{1}=mg
Ahora parece que nos hemos quedado sin cuerpos sobre los cuales aplicar el DCL, ya que no queremos a la tensión 1 sino a {T}_{2} . En este caso, aplicamos la primera ley de Newton en el punto de sujeción entre las cuerdas.
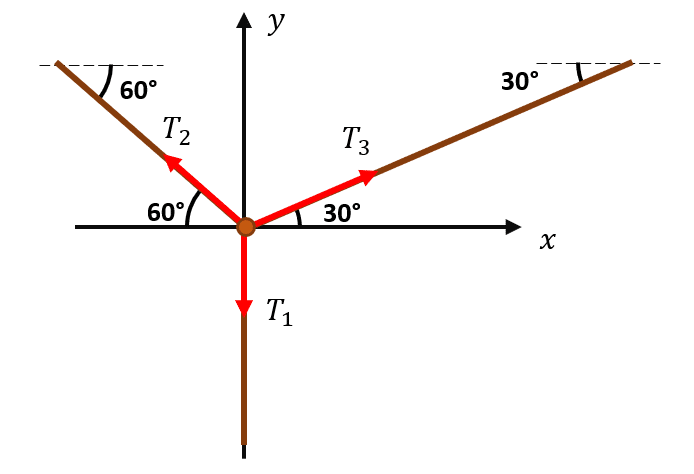
Descomponemos las fuerzas en los ejes x y y .
\sum {F}_{x}=0\to {T}_{3}\mathrm{cos}30-{T}_{2}\mathrm{cos}60=0
Obtenemos una relación entre las tensiones {T}_{3} y {T}_{2} .
{T}_{3}=\frac{\mathrm{cos}60}{\mathrm{cos}30}{T}_{2}
Aplicamos el mismo análisis en el eje y .
\sum {F}_{y}=0\to {T}_{2}\mathrm{sin}60+{T}_{3}\mathrm{sin}30-{T}_{1}=0
Sustituimos y despejamos a {T}_{2} .
{T}_{2}\mathrm{sin}60+\frac{\mathrm{cos}60\cdot \mathrm{sin}30}{\mathrm{cos}30}{T}_{2}-mg=0
{T}_{2}\left(\mathrm{sin}60+\mathrm{cos}60\cdot \mathrm{tan}30\right)=mg
{T}_{2}=\frac{mg}{\mathrm{sin}60+\mathrm{cos}60\cdot \mathrm{tan}30}
Sustituyendo valores obtenemos que:
{T}_{2}=2.88 \mathrm{N}
Comparando con los incisos, concluimos que la respuesta correcta es el b).
Reactivo 13
Calcule el trabajo que realiza una fuerza \overrightarrow{F}=\left(4.5, -5\right) \mathrm{N} , para desplazar una masa sobre un plano totalmente horizontal y cuya fricción respecto al suelo es nula, para llevarla por un camino recto de 2 metros.
- 12 J
- 4 J
- 10 J
- 9 J
Solución:
Para calcular el trabajo que realiza una fuerza al desplazar rectilíneamente una masa, debemos emplear la siguiente ecuación:
W={F}_{x}\cdot \mathrm{\Delta }x=F\cdot \mathrm{\Delta }x\cdot \mathrm{cos}\alpha
Tengamos en cuenta que {F}_{x} es la componente de la fuerza que apunta en la dirección del movimiento. Debido a que el problema nos indica directamente que la componente en x de la fuerza es 4.5 \mathrm{N} , solo nos queda sustituir y calcular directamente.
W=\left(4.5 \mathrm{N}\right)\left(2 \mathrm{m}\right)=9 \mathrm{J}
La fuerza genera 9 Joules de trabajo al desplazar a la masa.
Concluimos que la respuesta correcta es el inciso d).
Reactivo 14
Indique cuál de las siguientes aseveraciones es correcta desde el punto de vista de la estática.
- Las condiciones de estabilidad son: \sum \overrightarrow{\tau }=\overrightarrow{\alpha }I y \sum \overrightarrow{F}=\overrightarrow{a}m
- Si el eje de rotación de un sistema mecánico se coloca en el centro de masas, se aumenta el torque gravitacional total sobre el sistema
- Para un sistema de partículas, el centro de masas se encuentra sobre la partícula de mayor masa
- La estabilidad frente a torcas se logra en un sistema cuando el eje de rotación pasa por el centro de masas
Solución:
Para encontrar solución a este problema, debemos analizar cada uno de los enunciados teniendo en cuenta los postulados de la estática.
Aseveración A.
Las condiciones de estabilidad son: \sum \overrightarrow{\tau }=\overrightarrow{\alpha }I y \sum \overrightarrow{F}=\overrightarrow{a}m .
La estabilidad de un sistema mecánico implica que tanto su aceleración angular como su aceleración lineal son nulas, es decir, rotan y se desplazan a velocidad cero o constante. Estas aseveraciones son ciertas si y solo si \overrightarrow{\alpha }=0 y \overrightarrow{a}=0 . Esta aseveración no es correcta.
Aseveración B.
Si el eje de rotación de un sistema mecánico se coloca en el centro de masas, se aumenta el torque gravitacional total sobre el sistema.
Recordemos que el centro de masas de cualquier sistema físico, es un punto dentro de su geometría en el que las fuerzas gravitatorias actúan por igual en todas las direcciones, por tanto, las torcas debido a la gravedad se compensan mutuamente. Esta aseveración es también incorrecta.
Aseveración C.
Para un sistema de partículas, el centro de masas se encuentra sobre la partícula de mayor masa.
Esta aseveración es directamente incorrecta debido a que el centro de masas, en cualquier caso, es un punto cuyas coordenadas son un promedio ponderado de la posición y masa de las partículas que lo conforman, a menos que una de esas partículas sea mucho más masiva que el resto, la aseveración es incorrecta.
Aseveración D.
La estabilidad frente a torcas se logra en un sistema cuando el eje de rotación pasa por el centro de masas.
Como explicamos para la aseveración del inciso B, un eje de rotación perpendicular al plano del sistema y que pasa por el centro de masas garantiza que las torcas en un sentido se anulan completamente con las torcas en sentido contrario. Esta aseveración es correcta.
Concluimos que la respuesta correcta es el inciso d).
Reactivo 15
Se quiere realizar un experimento, en el que se deja caer libremente una pelota A desde lo alto de un edificio de 20 metros y al mismo tiempo se lanza verticalmente hacia arriba otra pelota B con una velocidad inicial de 5 m/s. Calcule teóricamente el punto de intersección de las pelotas sin considerar el efecto del viento y la aceleración de gravedad igual a 10 \mathrm{m}/{\mathrm{s}}^{2} .
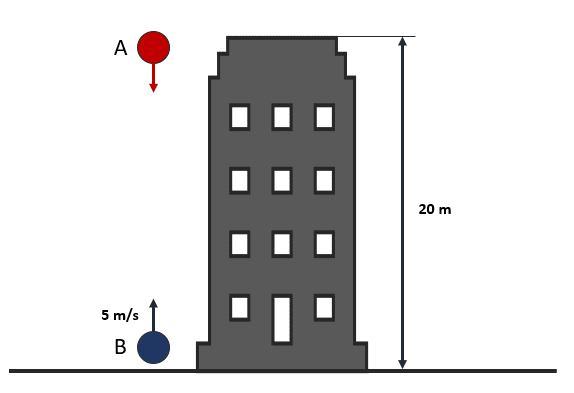
- 20 metros
- Nunca chocan en el aire
- 10 metros
- 5 metros
Solución:
En este caso, debemos calcular el punto de encuentro entre las dos pelotas para ello, primero obtenemos las ecuaciones de altura en función del tiempo para cada una y luego las igualamos para encontrar el instante de tiempo del choque. Comenzamos por la pelota A.
Cálculos para la pelota A.
{y}_{oA}=20 \mathrm{m},\mathrm{ }{v}_{oA}=0\mathrm{ }\mathrm{m}/\mathrm{s}
La ecuación de altura en función del tiempo quedaría:
{y}_{fA}={y}_{oA}+{v}_{oA}t-\frac{g{t}^{2}}{2}
Sustituimos y simplificamos.
{y}_{fA}=20+\left(0\right)t-5{t}^{2}\to {y}_{fA}=20-5{t}^{2}
Cálculos para la pelota B.
{y}_{oB}=0 \mathrm{m},\mathrm{ }{v}_{oA}=5\mathrm{ }\mathrm{m}/\mathrm{s}
En este caso, la ecuación de altura quedaría como:
{y}_{fB}={y}_{oB}+{v}_{oB}t-\frac{g{t}^{2}}{2}
Sustituimos.
{y}_{fB}=0+\left(5\right)t-5{t}^{2}\to {y}_{fB}=5t-5{t}^{2}
Igualamos las ecuaciones.
5t-5{t}^{2}=20-5{t}^{2}\to 5t=20
\therefore {t}_{choque}=4 \mathrm{s}
Ahora, sustituimos este valor en cualquiera de las ecuaciones para obtener la altura de impacto.
{y}_{fA}=20-5{\left(4\right)}^{2}=-60 \mathrm{m}
Comprobamos con las ecuaciones de B.
{y}_{fB}=5\left(4\right)-5{\left(4\right)}^{2}=-60 \mathrm{m}
Este resultado nos dice indirectamente que las pelotas nunca se tocan en el aire.
Concluimos que la respuesta correcta es la opción b).
Reactivo 16
Calcule la masa de un cuerpo que estando en reposo, experimenta una fuerza de 200 N durante 20 segundos que le hace recorrer una distancia de 100 m. Además, indique la rapidez pasados los 20 segundos.
- 400 \mathrm{k}\mathrm{g},\mathrm{ }10\mathrm{ }\mathrm{m}/\mathrm{s}
- 400 \mathrm{k}\mathrm{g},\mathrm{ }-10\mathrm{ }\mathrm{m}/\mathrm{s}
- 40 \mathrm{k}\mathrm{g},\mathrm{ }10\mathrm{ }\mathrm{m}/\mathrm{s}
- 4 \mathrm{k}\mathrm{g},\mathrm{ }-10\mathrm{ }\mathrm{m}/\mathrm{s}
Solución:
Para resolver este problema, debemos emplear la segunda ley de Newton.
F=ma
En este caso conocemos la fuerza, tenemos algunos datos para calcular la aceleración y podremos calcular la masa con la segunda ley de Newton. De las ecuaciones de cinemática sabemos que:
{x}_{f}={x}_{o}+{v}_{o}t+\frac{a{t}^{2}}{2}
El cuerpo parte del reposo y la posición inicial podemos asumirla igual a cero, por tanto:
{x}_{f}=\frac{a{t}^{2}}{2}
Despejamos la aceleración.
a=\frac{2{x}_{f}}{{t}^{2}}=\frac{2\left(100 \mathrm{m}\right)}{{\left(20 \mathrm{s}\right)}^{2}}=0.5 \mathrm{m}/{\mathrm{s}}^{2}
Calculamos la masa.
m=\frac{F}{a}=\frac{200 \mathrm{N}}{0.5 \mathrm{m}/{\mathrm{s}}^{2}}=400 \mathrm{k}\mathrm{g}
El cuerpo tiene una masa de 400 kg. Ahora, la velocidad final la obtenemos con la ecuación:
{v}_{f}={v}_{o}+at
Sustituimos.
{v}_{f}=\left(0.5 \mathrm{m}/{\mathrm{s}}^{2}\right)\left(20 \mathrm{s}\right)=10 \mathrm{m}/\mathrm{s}
El cuerpo termina su aceleración con una rapidez final de 10 m/s.
Comparando con los incisos, concluimos que la respuesta correcta es el a).
Reactivo 17
Si los bloques que se muestran en la figura tienen masas {m}_{1}=1 \mathrm{k}\mathrm{g} y {m}_{2}=0.8 \mathrm{k}\mathrm{g} , determine la aceleración que experimenta el bloque {m}_{2} .
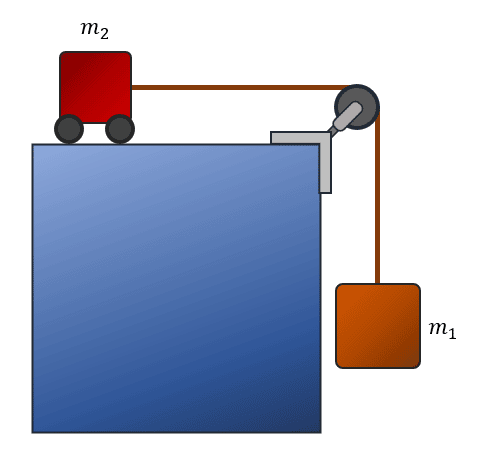
- -5.56\frac{\mathrm{m}}{{\mathrm{s}}^{2}}
- 5.56\frac{\mathrm{m}}{{\mathrm{s}}^{2}}
- 6\frac{\mathrm{m}}{{\mathrm{s}}^{2}}
- 55.6\frac{\mathrm{m}}{{\mathrm{s}}^{2}}
Solución:
A partir de la segunda ley de Newton, sabemos que la aceleración de un cuerpo depende de su masa y de la fuerza aplicada sobre él.
a=\frac{F}{m}
Del bloque 2 ya conocemos su masa, ahora solo nos queda determinar la fuerza que experimenta debido a la masa {m}_{1} . A partir de los DCL obtenemos que:
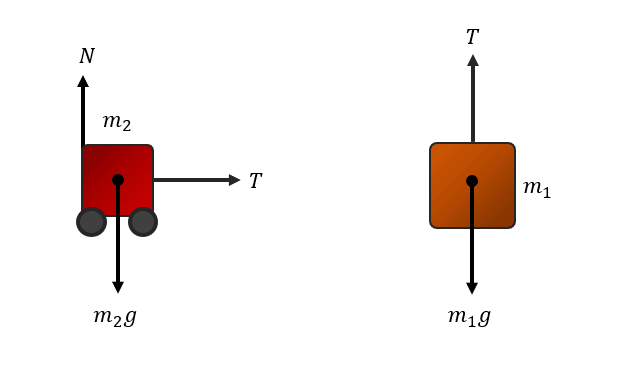
Para el bloque 1.
\sum {F}_{y}={m}_{1}a\to T-{m}_{1}g=-{m}_{1}a
Despejando la tensión.
T=\left(g-a\right){m}_{1}
Para el bloque 2.
\sum {F}_{x}={m}_{2}a\to T={m}_{2}a
No es necesario utilizar las ecuaciones en y para el bloque 2, porque el sistema carece de fricción. Igualamos las ecuaciones.
{m}_{2}a=g{m}_{1}-a\_{m}_{1}
Despejamos la aceleración.
a=\frac{g{m}_{1}}{{m}_{1}+{m}_{2}}
Sustituimos:
a=\frac{\left(10\frac{\mathrm{m}}{{\mathrm{s}}^{2}}\right)\left(1 \mathrm{k}\mathrm{g}\right)}{1 \mathrm{k}\mathrm{g}+0.8 \mathrm{k}\mathrm{g}}=5.56 \mathrm{m}/{\mathrm{s}}^{2}
El bloque {m}_{2} experimenta una aceleración de 5.56 \mathrm{m}/{\mathrm{s}}^{2} .
La respuesta correcta es el inciso b).
Reactivo 18
Calcule la velocidad inicial de un móvil que se desplaza con aceleración constante, si el mismo tarda 10 segundos en pasar por dos puntos de control, los cuales se encuentran a una distancia de 120 metros. Tenga en cuenta que la rapidez al pasar por el segundo punto fue de 20 m/s.
- 2\frac{\mathrm{m}}{\mathrm{s}}
- 1.6\frac{\mathrm{m}}{\mathrm{s}}
- 4\frac{\mathrm{m}}{\mathrm{s}}
- -4\frac{\mathrm{m}}{\mathrm{s}}
Solución:
Para resolver este problema de cinemática, comencemos por ordenar los datos que nos indica el enunciado mediante una gráfica de la situación planteada.
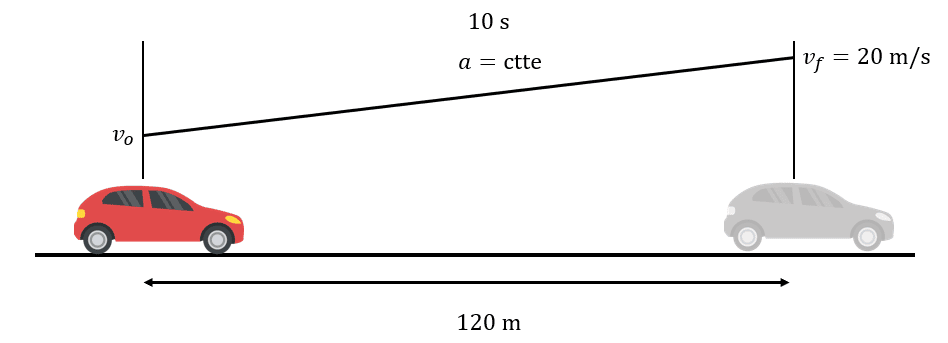
Recordemos las ecuaciones de cinemática para MUA:
{v}_{f}={v}_{o}+at
{x}_{f}={x}_{o}+{v}_{o}t+\frac{a{t}^{2}}{2}
En ambas ecuaciones tenemos dos incógnitas, por tanto, será necesario establecer un sistema de 2 ecuaciones con 2 incógnitas, comenzamos con la primera ecuación.
20={v}_{o}+10a\to {v}_{o}+10a=20 \left(I\right)
Vamos con la segunda.
120=0+10{v}_{o}+50a\to 10{v}_{o}+50a=120
Dividimos entre 10 toda la expresión.
{v}_{o}+5a=12 \left(II\right)
Restamos la primera ecuación con la segunda.
I-II:
{v}_{o}+10a-{v}_{o}-5a=20-12
5a=8\to a=1.6 \mathrm{m}/{\mathrm{s}}^{2}
Sustituimos en cualquiera de las ecuaciones para obtener a {v}_{o} .
{v}_{o}=20-\left(1.6\right)\left(10\right)=4 \mathrm{m}/\mathrm{s}
La rapidez inicial del móvil es de 4 metros por segundo.
La respuesta correcta es el inciso c).
Reactivo 19
Para el siguiente sistema totalmente estático, calcule la tensión que debe soportar la cuerda que se encuentra totalmente vertical.
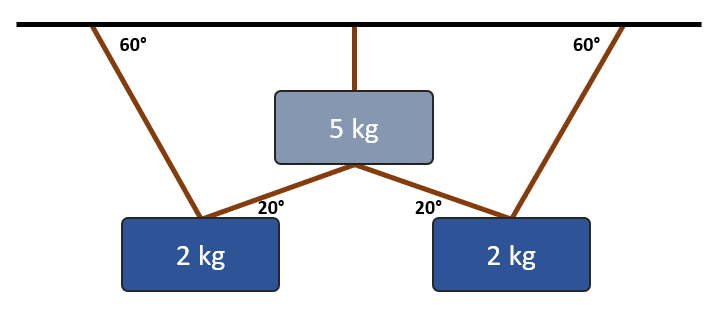
Considere a la aceleración de gravedad igual a 10 \mathrm{m}/{\mathrm{s}}^{2} .
- 5.95 \mathrm{N}
- 60 \mathrm{N}
- 56.95 \mathrm{N}
- 569.5 \mathrm{N}
Solución:
Teniendo en cuenta las condiciones de estabilidad de la mecánica clásica, en el sistema no ocurren rotaciones, por tanto, no es necesario considerar torcas. Por otro lado, las fuerzas de tensión en los ejes x y y son las que mantienen al sistema suspendido por las cuerdas, aplicamos la primera ley de Newton.
Comencemos por realizar el DCL de la masa de 5 kilogramos.
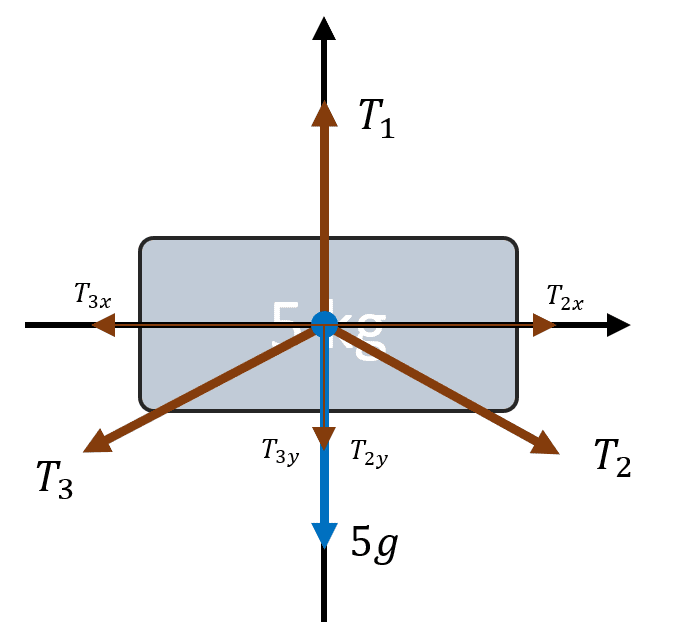
Descomponiendo las fuerzas en los ejes nos queda:
\sum {F}_{x}=0\to {T}_{2x}-{T}_{3x}=0
{T}_{2x}={T}_{3x}
Este resultado nos dice que, para lograr la estabilidad, las componentes en x de las tensiones {T}_{2} y {T}_{3} deben ser iguales y en sentido contrario para anularse.
\sum {F}_{y}=0\to {T}_{1}-{T}_{2y}-{T}_{3y}-5g=0
Despejamos a la tensión {T}_{1} .
{T}_{1}={T}_{2y}+{T}_{3y}+5g
Para calcular a {T}_{1} debemos encontrar a {T}_{2} y a {T}_{3} . Aplicamos DCL sobre la masa de la izquierda.
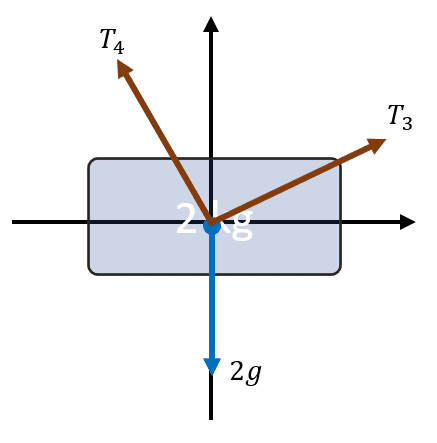
Descomponiendo las fuerzas nos queda:
\sum {F}_{x}=0\to {T}_{3x}-{T}_{4x}=0
Las componentes de las tensiones {T}_{4} y {T}_{3} son iguales y se anulan mutuamente.
\sum {F}_{y}=0\to {T}_{3y}+{T}_{4y}-2g=0
Si aplicamos DCL para la masa de la derecha, obtenemos algo similar.
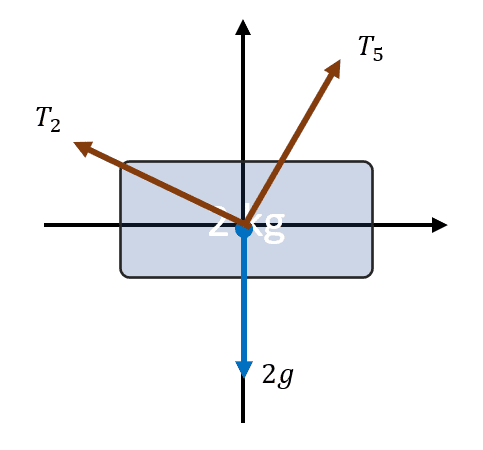
Descomponemos las fuerzas:
\sum {F}_{x}=0\to {T}_{5x}-{T}_{2x}=0
Las componentes de las tensiones {T}_{5} y {T}_{2} son iguales y se anulan mutuamente.
\sum {F}_{y}=0\to {T}_{2y}+{T}_{5y}-2g=0
Otra cosa que podemos concluir al analizar los DCL, es que la tensión {T}_{2} es igual en magnitud que {T}_{3} y que {T}_{4} es igual a {T}_{5} en magnitud, esto debido a que las masas y los ángulos son iguales. Podemos simplificar las ecuaciones aplicando el siguiente cambio:
{T}_{2}={T}_{3}={T}_{a}
{T}_{4}={T}_{5}={T}_{b}
Aplicando este cambio en la primera ecuación nos queda:
{T}_{1}={T}_{2y}+{T}_{3y}+5g={T}_{a}\mathrm{sin}20+{T}_{a}\mathrm{sin}20+5g
{T}_{1}=2{T}_{a}\mathrm{sin}20+5g \left(1\right)
Analizando ahora las ecuaciones del bloque izquierdo.
{T}_{3x}-{T}_{4x}=0\to {T}_{a}\mathrm{cos}20-{T}_{b}\mathrm{cos}60=0
{T}_{b}=\frac{\mathrm{cos}20}{\mathrm{cos}60}{T}_{a} \left(2\right)
Con las componentes en y de las fuerzas:
{T}_{3y}+{T}_{4y}-2g=0\to {T}_{a}\mathrm{sin}20+{T}_{b}\mathrm{sin}60-2g=0
Sustituimos la relación anterior.
{T}_{a}\mathrm{sin}20+\left(\frac{\mathrm{cos}20}{\mathrm{cos}60}{T}_{a}\right)\mathrm{sin}60-2g=0
{T}_{a}\mathrm{sin}20+\mathrm{cos}20\mathrm{tg}60{T}_{a}=2g
{T}_{a}=\frac{2g}{\mathrm{sin}20+\mathrm{cos}20\mathrm{tg}60} \left(3\right)
Sustituimos esto en la ecuación (1).
{T}_{1}=2\left(\frac{2g}{\mathrm{sin}20+\mathrm{cos}20\mathrm{tg}60}\right)\mathrm{sin}20+5g
{T}_{1}=\frac{4g\mathrm{sin}20}{\mathrm{sin}20+\mathrm{cos}20\mathrm{tg}60}+5g
Calculando obtenemos:
{T}_{1}=56.95 \mathrm{N}
La cuerda 1 debe soportar una tensión de 56.95 Newtons.
Concluimos que la respuesta correcta está en el inciso c).
Reactivo 20
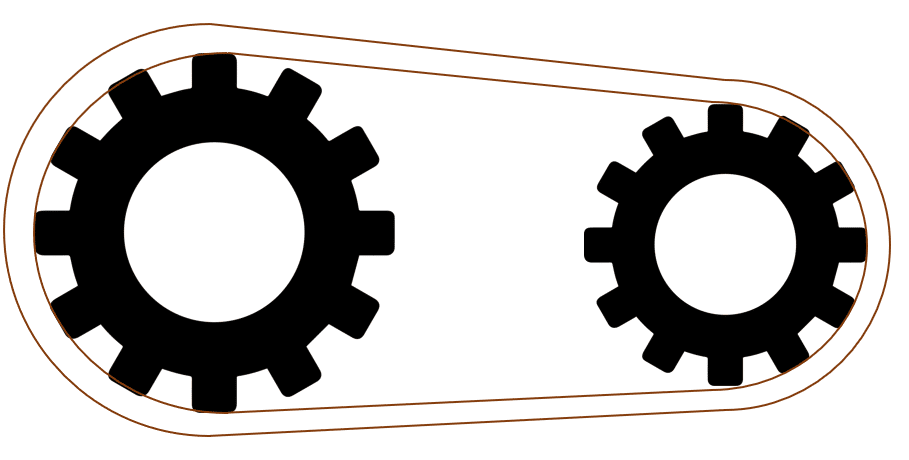
Se tienen dos engranajes de un sistema mecánico, los cuales se encuentran acoplados a través de una cadena con masa despreciable y sin rozamiento, tal como se muestra en la figura. Si la frecuencia de los engranajes 1 y 2 es {f}_{1}=20 \mathrm{H}\mathrm{z} y {f}_{2}=10 \mathrm{H}\mathrm{z} , y el radio medio del primer engranaje es de 30 cm, ¿cuál debería ser el radio del segundo engranaje para que tengan la misma velocidad lineal?
- 60 \mathrm{c}\mathrm{m}
- 6 \mathrm{c}\mathrm{m}
- 6 \mathrm{m}
- 0.6 \mathrm{c}\mathrm{m}
Solución:
A partir de las ecuaciones del movimiento circular, sabemos que la velocidad lineal se relaciona con la velocidad angular, a partir de la siguiente ecuación.
v=r\omega
Cada engranaje tiene un radio establecido, por tanto, las ecuaciones quedan como:
{v}_{1}={r}_{1}{\omega }_{1} y {v}_{2}={r}_{2}{\omega }_{2}
Igualamos las velocidades lineales.
{r}_{1}{\omega }_{1}={r}_{2}{\omega }_{2}
Ahora, no tenemos la velocidad angular de los engranajes, pero sí sus frecuencias, las cuales se relacionan con la velocidad angular según la siguiente ecuación:
\omega =2\pi f
Sustituyendo en la igualdad.
2\pi {f}_{1}{r}_{1}=2\pi {f}_{2}{r}_{2}
Simplificando nos queda:
{f}_{1}{r}_{1}={f}_{2}{r}_{2}
Despejando el radio del segundo engranaje nos queda:
{r}_{2}=\frac{{f}_{1}}{{f}_{2}}{r}_{1}=\frac{20 \mathrm{H}\mathrm{z}}{10 \mathrm{H}\mathrm{z}}\left(30 \mathrm{c}\mathrm{m}\right)=60 \mathrm{c}\mathrm{m}
El radio del segundo engranaje deber igual a 60 centímetros.
Concluimos indicando como correcta la opción a).

