Examen Simulador IPN de Física CSyA: Reactivos del 21 al 30

Seguimos con la tercera parte del examen simulador de física del área de ciencias sociales y administrativas del IPN, vamos a resolver los ejercicios del 21 al 30.

Reactivo 21

Calcular el alcance horizontal de un proyectil disparado por un cañón militar a una velocidad inicial de 800 \mathrm{m}/\mathrm{s} y un ángulo de 35° respecto de la horizontal. Tenga en cuenta g=10 \mathrm{m}/{\mathrm{s}}^{2} .

1. 30140 \mathrm{m}
2. 40140 \mathrm{m}
3. 50140 \mathrm{m}
4. 60140 \mathrm{m}

Solución:

Para resolver cualquier problema de lanzamiento de proyectiles, lo primero que debemos hacer es separar el análisis en dos movimientos distintos: uno UA para la componente vertical y otro MRU para la componente horizontal.

En este caso concreto, debemos calcular el tiempo de vuelo con el MUA en la vertical y con este dato finalmente obtener el desplazamiento horizontal. Comencemos descomponiendo la velocidad en cada una de las componentes x y y .

{v}_{ox}=800\mathrm{cos}35°=655.32 \mathrm{m}/\mathrm{s}

{v}_{oy}=800\mathrm{sin}35°=458.86 \mathrm{m}/\mathrm{s}

El tiempo de vuelo se calcula como:

{t}_{v}=\frac{2{v}_{oy}}{g}=\frac{2\left(458.86 \mathrm{m}/\mathrm{s}\right)}{10 \mathrm{m}/{\mathrm{s}}^{2}}=91.77 \mathrm{s}

Ahora, sustituimos este tiempo en la ecuación de movimiento horizontal:

{x}_{f}={x}_{o}+{v}_{x}t

{x}_{f}=\left(655.32 \mathrm{m}/\mathrm{s}\right)\left(91.77 \mathrm{s}\right)=60140 \mathrm{m}=60.14\mathrm{ }\mathrm{k}\mathrm{m}

Comparando con los incisos, concluimos que la respuesta correcta es el d).

Reactivo 22

Desde la azotea de un edificio se deja caer libremente una pelota. Pasado 1 segundo se lanza hacia abajo otra pelota con una rapidez inicial de 15 m/s. Determine la altura en la que se encuentran las pelotas.

1. Pasados 10 metros
2. Pasados 20 metros
3. Pasados 25 metros
4. Pasados 15 metros

Solución:

Este ejercicio consta en calcular la altura que tendrá la primera pelota pasado el segundo, y luego igualar las ecuaciones de altura en función del tiempo de ambos cuerpos para encontrar un intervalo de tiempo en el que sean iguales.

Calculamos la altura de la pelota 1 a transcurrido el segundo.

{y}_{1f}={y}_{1o}+{v}_{1o}t-\frac{g{t}^{2}}{2}

El enunciado no nos indica la altura del edificio, por tanto, asumimos que el cero de nuestro eje de coordenadas se encuentra en la azotea del edificio.

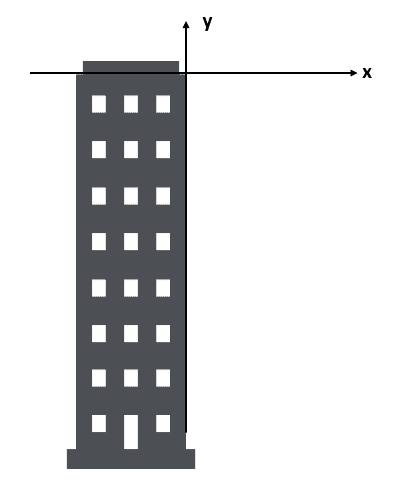
A partir de ahora, las alturas que midamos estarán referidas a este punto.

Sustituimos en la ecuación.

{y}_{1f}=-\frac{\left(10\frac{\mathrm{m}}{{\mathrm{s}}^{2}}\right){\left(1 \mathrm{s}\right)}^{2}}{2}=-5 \mathrm{m}

Ahora, esta será la velocidad inicial de la primera pelota para compararla con la segunda. Calculamos también su velocidad en este punto.

{v}_{1f}={v}_{1o}-gt=-\left(10\frac{\mathrm{m}}{{\mathrm{s}}^{2}}\right)\left(1 \mathrm{s}\right)=-10\frac{\mathrm{m}}{\mathrm{s}}

La ecuación de altura en función del tiempo para la segunda pelota sería, a partir de este punto:

{y}_{1f}=-5-10t-5{t}^{2}

Obtenemos la misma ecuación para la segunda pelota.

{y}_{2f}={y}_{2o}+{v}_{2o}t-\frac{g{t}^{2}}{2}

Sustituimos.

{y}_{2f}=-15t-5{t}^{2}

Igualamos las ecuaciones:

-15t-5{t}^{2}=-5-10t-5{t}^{2}

Simplificamos y despejamos al tiempo.

15t-10t=5\to 5t=5

t=1 \mathrm{s}

Transcurre un segundo para las pelotas se encuentren luego de lanzar a la pelota 2. Sustituimos este resultado en cualquiera de las ecuaciones para obtener la altura de impacto.

{y}_{2f}=-15\left(1\right)-5\left(1\right)=-20 \mathrm{m}

Concluimos que a los 20 metros las pelotas se chocan.

Concluimos que la respuesta correcta es el inciso b).

Reactivo 23

Encuentre la expresión para calcular el tiempo de vuelo para un proyectil disparado en tiro parabólico.

1. {t}_{v}=2{v}_{oy}
2. {t}_{v}=\frac{{v}_{oy}}{2g}
3. {t}_{v}=\frac{{v}_{oy}}{g}
4. {t}_{v}=\frac{2{v}_{oy}}{g}

Solución:

Para obtener la ecuación del tiempo de vuelo de un proyectil disparado en tiro parabólico, debemos recordar que el movimiento es simétrico respecto a la altura máxima, por tanto, nos basta con calcular el tiempo que tarda en llegar a la altura máxima y multiplicarlo por 2.

Por otro lado, estamos asumiendo que la altura inicial es cero {y}_{o}=0 . Además, en la altura máxima la velocidad en y se anula.

{v}_{fy}={v}_{oy}-gt\to {t}_{max}=\frac{{v}_{oy}}{g}

Gracias a esta simetría, solo nos queda multiplicar por 2.

{t}_{v}=\frac{2{v}_{oy}}{g}

Concluimos que la respuesta correcta es el inciso d).

Reactivo 24

En la siguiente figura se muestra la gráfica de velocidad en función del tiempo para el movimiento de un cuerpo.

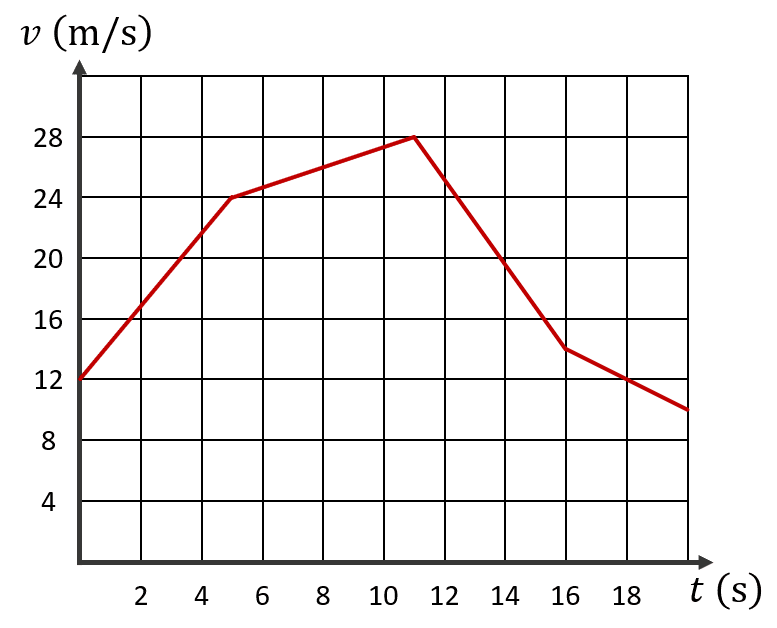
Teniendo en cuenta que el móvil parte desde cero, calcule el desplazamiento total.

1. 500 m
2. 399 m
3. 400 m
4. 250 m

Solución:

El desplazamiento total del móvil lo podemos calcular como la suma de los desplazamientos en cada intervalo donde la pendiente de la velocidad permanece constante. Examinando el gráfico, estos serían las distintas etapas del movimiento.

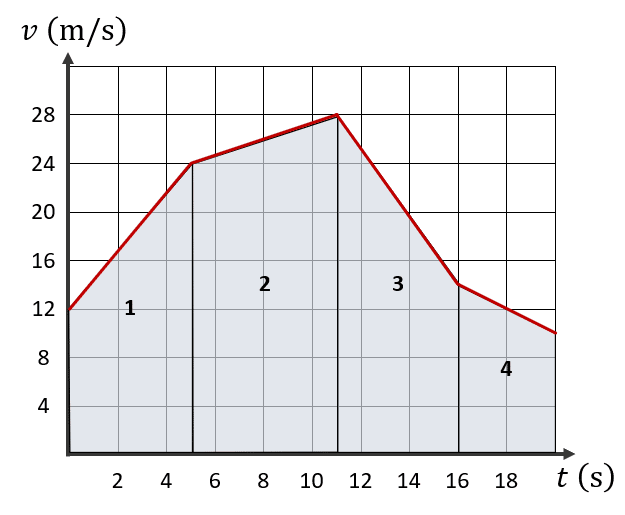
{d}_{t}={d}_{1}+{d}_{2}+{d}_{3}+{d}_{4}

Ahora, podríamos utilizar las ecuaciones clásicas de la cinemática para calcular el desplazamiento en cada intervalo y luego sumarlos. Esto no es incorrecto, pero sería un proceso largo y tardío. En su lugar, vamos a aprovechar la gráfica para aplicar un concepto bastante importante que relaciona la velocidad y el desplazamiento:

El área bajo la curva de velocidad, es igual al desplazamiento del móvil en dicho intervalo.

Con esta premisa, nuestro problema se acaba de convertir en uno totalmente geométrico que consta en calcular el área de cada uno de los trapecios.

{A}_{t}=\frac{b\left({h}_{2}+{h}_{1}\right)}{2}

Calculamos el área de cada paralelogramo.

{A}_{1}=\frac{\left(5\right)\left(24+12\right)}{2}=90 \mathrm{m}

{A}_{2}=\frac{6\left(28+24\right)}{2}=156 \mathrm{m}

{A}_{3}=\frac{5\left(28+14\right)}{2}=105 \mathrm{m}

{A}_{4}=\frac{4\left(14+10\right)}{2}=48 \mathrm{m}

El desplazamiento total fue de:

{d}_{t}=90+156+105+48=399 \mathrm{m}

Concluimos que la respuesta correcta es la b).

Reactivo 25

La ley de Coulomb establece que la fuerza de atracción o repulsión entre dos cargas es inversamente proporcional a…

1. El cuadrado de la constante eléctrica
2. El cuadrado del momento dipolar magnético
3. El cuadrado de la distancia
4. La distancia

Solución:

La Ley de Coulomb es uno de los postulados fundamentales de la electrostática y una de las herramientas fundamentales a la hora de entender las interacciones entre cargas estáticas. Esta ley nos dice que:

La fuerza eléctrica entre dos cargas, es directamente proporcional a la constante eléctrica y al producto de las magnitudes de las cargas, e inversamente proporcional al cuadrado de la distancia.

F=\frac{{k}_{e}\left|{q}_{1}\right|\left|{q}_{2}\right|}{{d}^{2}}

Teniendo en cuenta esto y considerando los incisos, concluimos que la respuesta correcta es la c).

Reactivo 26

Se tienen tres cargas eléctricas dispuestas tal como indica la figura. Si {q}_{1}=+3\times {10}^{-3} \mathrm{C} , {q}_{2}=+2.5\times {10}^{-3} \mathrm{C} y {q}_{3}=-1\times {10}^{-3} \mathrm{C} , calcule la fuerza total sobre la carga {q}_{1} . Considere {k}_{e}=9\times {10}^{9}\frac{\mathrm{N}\cdot \mathrm{m}}{\mathrm{C}} .

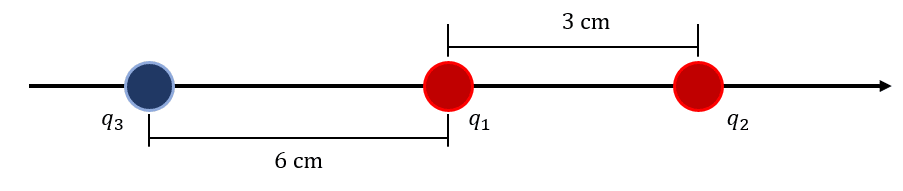
1. 8.5\times {10}^{6} \mathrm{N}\mathrm{ }\left(-\widehat{i}\right)
2. 8.25\times {10}^{6} \mathrm{N}\mathrm{ }\left(-\widehat{i}\right)
3. 0.825\times {10}^{6} \mathrm{N}\mathrm{ }\left(-\widehat{i}\right)
4. 82.5\times {10}^{6} \mathrm{N}\mathrm{ }\left(-\widehat{i}\right)

Solución:

Para encontrar la fuerza resultante sobre la carga {q}_{1} , debemos calcular por separado la fuerza en {q}_{1} debido a {q}_{2} y luego debido a {q}_{3} para finalmente aplicar sumatoria de fuerzas sobre {q}_{1} . Debemos tener presente la dirección de cada fuerza, ya que debemos trabajar con vectores.

{F}_{1}={F}_{12}+{F}_{13}

Fuerza debido a {q}_{2} .

Ya que {q}_{1} y {q}_{2} tienen la misma carga (positiva), la fuerza que experimenta {q}_{1} es de repulsión, es decir, en dirección -x .

{F}_{12}=\frac{{k}_{e}\left|{q}_{1}\right|\left|{q}_{2}\right|}{{d}_{12}^{2}}\left(-\widehat{i}\right)

Sustituimos.

{F}_{12}=\frac{\left(9\times {10}^{9}\frac{\mathrm{N}\cdot \mathrm{m}}{\mathrm{C}}\right)\left|3\times {10}^{-3} \mathrm{C}\right|\left|2.5\times {10}^{-3} \mathrm{C}\right|}{{\left(0.03 \mathrm{m}\right)}^{2}}\left(-\widehat{i}\right)=75\times {10}^{6} \mathrm{N}\mathrm{ }\left(-\widehat{i}\right)

Fuerza debido a {q}_{3} .

Ya que las cargas {q}_{1} y {q}_{3} tienen signos opuestos, la fuerza que experimenta {q}_{1} respecto a 3 es de atracción y en dirección a las -x .

{F}_{13}=\frac{{k}_{e}\left|{q}_{1}\right|\left|{q}_{3}\right|}{{d}_{13}^{2}}\left(-\widehat{i}\right)

Sustituimos.

{F}_{13}=\frac{\left(9\times {10}^{9}\frac{\mathrm{N}\cdot \mathrm{m}}{\mathrm{C}}\right)\left|3\times {10}^{-3} \mathrm{C}\right|\left|-1\times {10}^{-3} \mathrm{C}\right|}{{\left(0.06 \mathrm{m}\right)}^{2}}\left(-\widehat{i}\right)=7.5\times {10}^{6} \mathrm{N}\mathrm{ }\left(-\widehat{i}\right)

Calculamos la fuerza resultante en {q}_{1} .

{F}_{1}=75\times {10}^{6} \mathrm{N}\mathrm{ }\left(-\widehat{i}\right)+7.5\times {10}^{6} \mathrm{N}\mathrm{ }\left(-\widehat{i}\right)=82.5\times {10}^{6} \mathrm{N}\mathrm{ }\left(-\widehat{i}\right)

Comparando con las opciones, concluimos que la respuesta correcta es el inciso d).

Reactivo 27

¿En qué sentido van las líneas de campo eléctrico para una carga eléctrica positiva?

1. Hacia afuera y perpendiculares a la carga
2. Hacia el interior y perpendiculares a la carga
3. Hacia el interior y con cualquier ángulo a la carga
4. Hacia afuera y con el mínimo ángulo a la carga

Solución:

Uno de los primeros resultados que puede extraerse de la electroestática, es que las líneas de campo eléctrico son perpendiculares a las superficies des la que salen o entran. Además, las líneas de campo salen de las cargas positivas y entran hacia las negativas.

Concluimos que la respuesta correcta es el inciso a).

Reactivo 28

El potencial eléctrico en un punto del espacio se define como…

1. La energía necesaria para separar los electrones de sus átomos
2. La energía mecánica necesaria para desplazar una carga
3. La energía potencial por unidad de carga
4. La carga eléctrica necesaria para desplazar a otra

Solución:

La energía potencial es una cantidad escalar muy importante en electroestática, electricidad y electrónica, ya que permite simplificar los cálculos a la hora de tratar con sistemas eléctricos.

Su símbolo es V y se define como la energía potencial eléctrica que adquiere una unidad de carga positiva en determinado punto del espacio.

V=\frac{{E}_{p}}{q}

Comparando con los incisos, concluimos que la respuesta correcta está en el c).

Reactivo 29

Si la fuerza de atracción entre dos cargas eléctricas es de 20 N, ¿cuánto incrementa o disminuye la fuerza si la distancia se acorta a \frac{2}{3} de la distancia original?

1. 15 N
2. 25 N
3. 35 N
4. 45 N

Solución:

Para resolver este problema, debemos recordar la ecuación de fuerza eléctrica que nos brinda la Ley de Coulomb.

{F}_{e}=\frac{{k}_{e}{q}_{1}{q}_{2}}{{d}^{2}}

En este caso las cargas permanecen constantes, lo único que cambia es la distancia donde: {d}_{2}=\frac{2}{3}{d}_{1} según el enunciado. Tenemos para cada caso:

{F}_{1}=20=\frac{{k}_{e}{q}_{1}{q}_{2}}{{d}_{1}^{2}}

{F}_{2}=\frac{{k}_{e}{q}_{1}{q}_{2}}{{d}_{2}^{2}}=\frac{{k}_{e}{q}_{1}{q}_{2}}{\frac{4{d}_{1}^{2}}{9}}=\frac{9}{4}\cdot \frac{{k}_{e}{q}_{1}{q}_{2}}{{d}_{1}^{2}}

Sustituyendo \frac{{k}_{e}{q}_{1}{q}_{2}}{{d}_{1}^{2}}={F}_{1} nos queda:

{F}_{2}=\frac{9}{4}\left(20 \mathrm{N}\right)=45 \mathrm{N}

La fuerza incrementa a 45 Newtons.

La respuesta está en el inciso d).

Reactivo 30

Una persona se encuentra instalando una estufa eléctrica en su casa, pero no sabe cuanta corriente debe soportar el cableado y las instrucciones no son claras. Se sabe que la estufa consume una potencia máxima de 1200 W y que será conectado a una red eléctrica de 120 V. Calcule la ampacidad del cableado.

1. 5 A
2. 10 A
3. 15 A
4. 20 A

Solución:

Sabemos que la potencia eléctrica se calcula como:

P=VI

En este caso conocemos la potencia y el voltaje, por tanto, podemos despejar de forma directa la corriente.

I=\frac{P}{V}=\frac{1200\mathrm{W}}{120\mathrm{V}}=10 \mathrm{A}

El cableado debe soportar unos 10 amperios de corriente para instalar la estufa eléctrica.

La respuesta correcta es el inciso b).