En este post vamos a desarrollar la cuarta parte de la guía de ingreso a la Universidad de Guadalajara en el área de matemáticas. Antes de seguir, recuerda resolver los reactivos por tu cuenta, luego regresa para comprobar el procedimiento y aclarar dudas.

Consulta el resto de partes de la guía UDG resuelta de matemáticas haciendo click en los botones de navegación. El área de Matemáticas es solo una de las 4 que conforman la PAA.
Guía UDG resuelta Parte IV
La prueba de aptitud académica aplicada por la Universidad de Guadalajara es elaborada por el Collage Board y cuenta con la siguiente estructura:
- Lectura (45 reactivos).
- Redacción (25 reactivos).
- Matemáticas (55 reactivos).
- Inglés (50 reactivos).
Curso UDG
Reactivo 31: Variación de una función
Si f\left(x\right)=2x+3 y x aumenta 5 unidades, ¿Cuántas unidades aumenta f\left(x\right) ?
- 5
- 8
- 10
- 13
Solución:
Para calcular la variación en y respecto a una variación en x , debemos sustituir, hipotéticamente, un {x}_{1} y un {x}_{2} en la función para obtener un {y}_{1} y un {y}_{2} .
Luego, hacemos la resta {y}_{2}-{y}_{1} que sería igual a \Delta y , reacomodamos el lado de las x para que solo quede {x}_{2}-{x}_{1} , diferencia que es equivalente a \Delta x cuyo valor conocemos por el enunciado.
Sustituyendo {x}_{1} .
{y}_{1}=2{x}_{1}+3
Sustituyendo {x}_{2} .
{y}_{2}=2{x}_{2}+3
Hacemos la diferencia {y}_{2}-{y}_{1} .
{y}_{2}-{y}_{1}=2{x}_{2}+3-2{x}_{1}-3
\Delta y=2\left({x}_{2}-{x}_{1}\right)=2\Delta x
\therefore \Delta y=2\Delta x
Por último, sustituimos \Delta x=5 .
\Delta y=2\left(5\right)=10
Comparando con las opciones, seleccionamos como correcta la C.
Reactivo 32: Expresiones equivalentes
¿Cuál es el valor para b de manera que la ecuación 3+2\left(\frac{x+4}{x-1}\right)=b tenga la misma solución que \frac{x+4}{x-1}=6 ?
- 6
- 7
- 15
- 30
Solución:
En este caso, tomaremos toda la expresión \frac{x+4}{x-1} como una sola variable que llamaremos w . De esta forma, podemos reescribir la primera ecuación como:
3+2\left(\frac{x+4}{x-1}\right)=b\to 3+2w=b
De la segunda ecuación, sabemos que \frac{x+4}{x-1}=w=6 , sustituimos en la primera w=6 para encontrar el valor de b .
3+2w=b\to 3+2\left(6\right)=b
b=3+12=15
Concluimos entonces que: b debe ser igual a 15 para que 3+2\left(\frac{x+4}{x-1}\right)=b sea equivalente a \frac{x+4}{x-1}=6 .
Comparando con las opciones, la respuesta correcta se encuentra en el inciso C.
Reactivo 33: Solución de ecuaciones
Si para cierto valor de a la solución de la ecuación \sqrt{x}+a\sqrt{x+3}=3 es x=1 , entonces para ese mismo valor de a , ¿Cuál es la solución de a\sqrt{x-3}=1 ?
- -2
- -1
- 2
- 4
Solución:
Debemos sustituir en la expresión \sqrt{x}+a\sqrt{x+3}=3 a x=1 para hallar el valor de a . Con dicho valor, nos vamos a la expresión a\sqrt{x-3}=1 y despejamos a x .
Sustituyendo x=1 .
\sqrt{x}+a\sqrt{x+3}=3\to \sqrt{1}+a\sqrt{1+3}=3
1+a\sqrt{4}=3
2a=2\to a=1
Sustituimos a=1 en a\sqrt{x-3}=1 .
\left(1\right)\sqrt{x-3}=1\to \sqrt{x-3}=1
Despejamos la solución para x .
\sqrt{x-3}=1\to x-3=1
x=1+3\to x=4
Concluimos indicando que la respuesta correcta al problema es la opción D.
Reactivo 34: Trigonometría
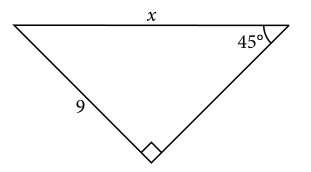
Halle la medida del lado x del triángulo que se muestra en la figura anterior.
- 9\sqrt{2}
- 9\sqrt{3}
- 3\sqrt{2}
- 2\sqrt{3}
Solución:
El triángulo rectángulo que se muestra en la figura del problema es rectángulo, porque uno de sus ángulos internos es de 90° y el lado marcado como x , que se encuentra frente al ángulo recto, es la hipotenusa del triángulo.
En este caso, debemos emplear una identidad trigonométrica que relacione al ángulo de 45°, el lado opuesto de 9 unidades y a la hipotenusa; esta descripción corresponde a la del seno del ángulo.
sin\alpha =\frac{CO}{H}
Sustituimos.
sin45 =\frac{9}{x}\to x=\frac{9}{sin45 }
El seno de 45° es \frac{\sqrt{2}}{2} .
x=\frac{9}{\frac{\sqrt{2}}{2}}=\frac{18}{\sqrt{2}}=9\sqrt{2}
Comparando con las opciones del problema, escogemos como correcta la A.
Reactivo 35: Arcos y cuerdas en la circunferencia
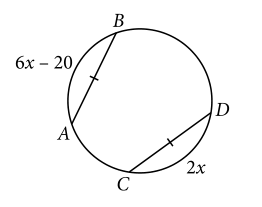
En la figura anterior, AB\cong CD . ¿Cuál es la medida del arco AB ?
- 54
- 30
- 27
- 10
Solución:
Para resolver este problema emplearemos una propiedad sobre las cuerdas y arcos en una circunferencia que dice:
A dos cuerdas iguales, les corresponde arcos iguales y viceversa.
En nuestro caso, se nos indica que las cuerdas AB y CD son aproximadamente iguales (las tomaremos como iguales) y por ellos sus arcos son también iguales.
AB=CD\to 6x-20=2x
Con esta expresión despejamos el valor de x .
6x-20=2x
4x=20
x=5
Finalmente, para conocer cuánto miden los arcos, sustituimos x=5 en 6x-20 .
\widehat{AB}=6\left(5\right)-20=10
Escogemos como correcta a la opción D.
Reactivo 36: Relaciones entre ángulos
Si dos ángulos son complementarios y sus medidas son x y x-20 , ¿Cuál es el valor de x , en grados?
- 50
- 55
- 100
- 110
Solución:
Dos ángulos son complementarios, si la suma de sus magnitudes es igual a un ángulo recto o de 90°. Tomando esta definición como base, podemos calcular el valor de x como:
x+x-20=90
Despejamos.
2x=110
\therefore x=55°
El valor de x en grados es 55.
Comparando con las opciones, la respuesta correcta se encuentra en el inciso B.
Reactivo 37: Ángulos entre rectas secantes
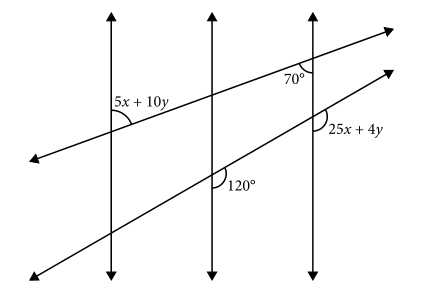
En la figura anterior, las tres rectas verticales son paralelas. ¿Cuál es el valor de x ?
- 4
- 5
- 9
- 18
Solución:
Cuando una misma recta corta a dos o más rectas paralelas entre sí, los ángulos alternos y correspondientes que se forman son iguales.
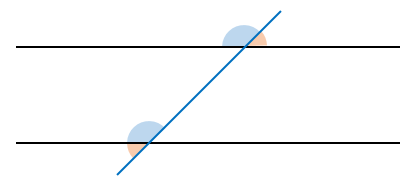
En la figura, puede verse que los ángulos en azul son correspondientes y los pintados de naranja son alternos. Trasladando esto a la imagen del problema, 5x+10y y 70° son alternos, mientras que 25x+4y y 120° son correspondientes.
5x+10y=70
25x+4y=120
Con estas dos ecuaciones tenemos un sistema 2×2 para encontrar el valor de x . Emplearemos el método por sustitución en este caso, despejamos la y de la segunda ecuación y la sustituimos en la primera.
4y=120-25x\to y=\frac{120-25x}{4}
Sustituimos.
5x+10\left(\frac{120-25x}{4}\right)=70
Multiplicamos por 4.
20x+10\left(120-25x\right)=280
Dividimos por 10.
2x+120-25x=28
-23x+120=28
23x=92
x=4
El valor de x es 4.
Concluimos el problema seleccionando como correcta a la opción A.
Reactivo 38: Volumen de solidos regulares
Un tanque de agua, con forma de prisma rectangular, mide 25 metros de largo por 10 metros de ancho por 5 metros de alto. ¿Cuál es el volumen de este tanque en metros cúbicos?
- 1250
- 1100
- 940
- 860
Solución:
Un prisma rectangular (también conocido como octaedro), es un sólido formado por dos caras rectangulares iguales una encima de otra y 4 caras laterales que encierran el interior del prisma. Para calcular su volumen, debemos multiplicar la altura por el área de la base.
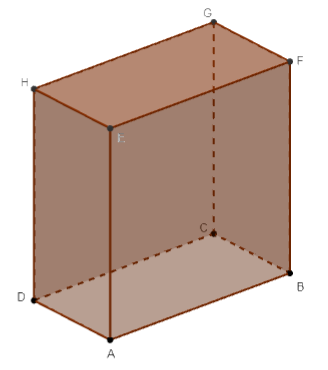
El área de la base es ancho por largo.
{A}_{b}=a*l=10 m*25 m=250 {m}^{2}
Ahora, para obtener el volumen multiplicamos la altura por el área de la base.
{V}_{p}=h*{A}_{b}=5 m*250 {m}^{2}=1250 {m}^{3}
El volumen del prisma es 1250 metros cúbicos.
Escogemos como respuesta correcta a la opción A.
Reactivo 39: El circulo
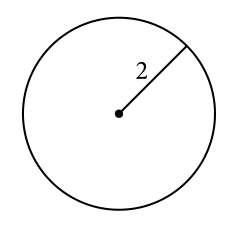
Si se duplica el radio del círculo anterior, el número de veces que aumenta el área del círculo es:
- 2
- 4
- 8
- 16
Solución:
La fórmula para calcular el área de un círculo es:
{A}_{c}=\pi {r}^{2}
Al inicio, el círculo tiene como radio r=2 por lo que su área es:
{A}_{c1}=\pi {\left(2\right)}^{2}=4\pi
Luego, el radio aumenta al doble del tamaño inicial, es decir, va de 2 a 4 por lo que el nuevo valor de área es:
{A}_{c2}=\pi {\left(4\right)}^{2}=16\pi
Para determinar en cuanta proporción aumento el área luego de duplicar el radio, hacemos el cociente \frac{{A}_{c2}}{{A}_{c1}} .
\frac{{A}_{c2}}{{A}_{c1}}=\frac{16\pi }{4\pi }=4
\therefore {A}_{c2}=4{A}_{c1}
El área aumenta en 4 veces su valor inicial cuando el radio aumenta el doble.
Comparando con las opciones, la respuesta correcta está en el inciso B.
Reactivo 40: Volumen de un cono circular
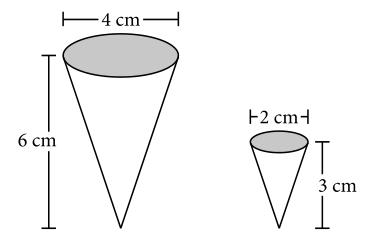
La figura anterior muestra dos conos circulares. Si el volumen de un cono circular está dado por V=\frac{\pi }{3}{r}^{2}h donde r es el radio y h es la altura del cono, ¿Cuál es la razón del volumen del cono pequeño al volumen del cono mayor?
- \frac{1}{8}
- \frac{\pi }{24}
- \frac{\pi }{8}
- \frac{1}{2}
Solución:
En este caso, debemos encontrar el cociente \frac{{V}_{cp}}{{V}_{cg}} entre el cono pequeño y el cono grande. Para la altura y el radio de cada solido nos referimos como: {h}_{g} y {r}_{g} para el cono grande y; {h}_{p} y {r}_{p} para el cono pequeño respectivamente.
De esta forma, el volumen de cada solido puede expresarse como:
{V}_{cp}=\frac{\pi }{3}{r}_{p}^{2}{h}_{p}
{V}_{cg}=\frac{\pi }{3}{r}_{g}^{2}{h}_{g}
Hacemos el cociente.
\frac{{V}_{cp}}{{V}_{cg}}=\frac{\frac{\pi }{3}{r}_{p}^{2}{h}_{p}}{\frac{\pi }{3}{r}_{g}^{2}{h}_{g}}=\frac{{r}_{p}^{2}{h}_{p}}{{r}_{g}^{2}{h}_{g}}
A partir de la imagen sabemos que:
{r}_{g}=\frac{4}{2}=2 cm
{h}_{g}=6 cm
{r}_{p}=\frac{2}{2}=1 cm
{h}_{p}=3 cm
Sustituimos.
\frac{{V}_{cp}}{{V}_{cg}}=\frac{{\left(1\right)}^{2}\left(3\right)}{{\left(2\right)}^{2}\left(6\right)}=\frac{3}{24}=\frac{1}{8}
La razón entre el volumen del cono pequeño y el cono grande es \frac{1}{8} .
Seleccionamos como respuesta correcta al inciso A.
