Este es el último de 5 post sobre la guía UDG resuelta en el área de matemáticas. Acá podrás consultar la solución a los reactivos del 41 al 55 para la prueba de ingreso a la UDG elaborada por el Collage Board.

¡Felicidades aspirante! ya solo quedan 15 reactivos para culminar el área de matemáticas en la guía de estudio. Recuerda que la PAA consta de otras 3 asignaturas y cada una tiene puntos clave que debes dominar antes presentar.
Guía UDG resuelta Parte V
El examen de admisión a la Universidad de Guadalajara se compone de 175 reactivos, con una duración de 3 horas. La división de los temas cuenta con la siguiente estructura:
- Lectura (45 reactivos).
- Redacción (25 reactivos).
- Matemáticas (55 reactivos).
- Inglés (50 reactivos).
Curso UDG
Reactivo 41: Cálculo de área
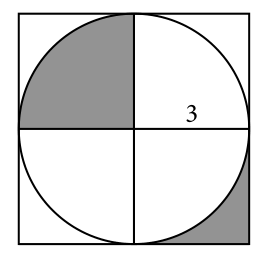
En la figura anterior hay un círculo inscrito en un cuadrado. ¿Cuántas unidades cuadradas mide la parte sombreada?
- 3
- 3\pi
- 9
- 9\pi
Solución:
El problema nos pide calcular el total del área sombreada en la figura. Tenemos dos zonas: un sector circular que representa un cuarto de círculo y una sección curva de contorno rectangular en la parte inferior derecha.
A la primera la llamaremos {A}_{sc} y a la segunda {A}_{id} .
{A}_{s}={A}_{sc}+{A}_{id}
Cálculo de {A}_{sc} .
Ya que representa a una sección circular de arco igual a 90°, podemos calcular su área al dividir el área del círculo entre 4.
{A}_{sc}=\frac{{A}_{c}}{4}=\frac{\pi {r}^{2}}{4}
A partir de la imagen sabemos que el radio es igual a 3.
{A}_{sc}=\frac{\pi {\left(3\right)}^{2}}{4}=\frac{9\pi }{4}
Cálculo de {A}_{id} .
El área sombreada en la esquina inferior derecha, es equivalente a tomar el área del cuadrado en esa zona de lado igual a 3 y restarle el área de un cuarto del círculo.
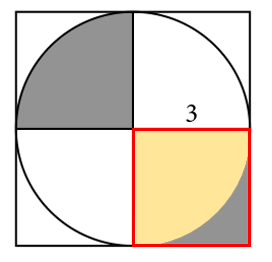
{A}_{id}={A}_{r}-{A}_{\frac{c}{4}}
El área de un cuarto de círculo lo obtenemos del paso anterior.
{A}_{id}={3}^{2}-\frac{9\pi }{4}=9-\frac{9\pi }{4}
Finalmente, calculamos lo solicitado.
{A}_{s}=\frac{9\pi }{4}+9-\frac{9\pi }{4}=9 {u}^{2}
El área sombreada total mide 9 unidades cuadradas.
Inspeccionando los incisos del problema, indicamos como respuesta correcta la opción C.
Reactivo 42: Área entre círculos
El diámetro de un círculo es el triple del de otro círculo más pequeño. ¿Cuál es la razón del área del círculo más grande al área del círculo más pequeño?
- \frac{9}{4}
- \frac{3}{2}
- 6
- 9
Solución:
Recordemos la fórmula para calcular el área de un círculo en términos del diámetro:
{A}_{c}=\frac{\pi {d}^{2}}{4}
Por el enunciado, sabemos que el diámetro del círculo más grande es 3 veces el diámetro del pequeño.
{d}_{g}=3{d}_{p}
De esta forma, el área de cada círculo queda como:
{A}_{cp}=\frac{\pi {d}_{p}^{2}}{4}
{A}_{cg}=\frac{\pi {d}_{g}^{2}}{4}=\frac{\pi {\left(3{d}_{p}\right)}^{2}}{4}=\frac{9\pi {d}_{p}^{2}}{4}
Hacemos el cociente \frac{{A}_{cg}}{{A}_{cp}} .
\frac{{A}_{cg}}{{A}_{cp}}=\frac{\frac{9\pi {d}_{p}^{2}}{4}}{\frac{\pi {d}_{p}^{2}}{4}}
Simplificando nos queda:
\frac{{A}_{cg}}{{A}_{cp}}=9
El área del círculo más grande es 9 veces mayor al área del círculo pequeño.
Finalizamos el problema escogiendo como respuesta correcta al inciso D.
Reactivo 43: Perímetro circular
Se instala una verja a 7 pies a la redonda del borde de una piscina circular de 10 pies de diámetro. ¿Cuál de las siguientes opciones expresa la longitud, en pies, de la verja?
- 12\pi
- 14\pi
- 17\pi
- 24\pi
Solución:
En este problema, se nos pide calcular el perímetro que tendrá la verja. Para ello, es necesario conocer el diámetro o radio que tendrá la misma.
El problema no indica de forma directa el valor del radio, pero nos dice que se construirá alrededor de una piscina de diámetro 10 pies (radio 5 pies) y que estará a 7 pies a la redonda de dicho borde.
Es decir, la verja será concéntrica respecto a la piscina y la distancia entre sus bordes es de 7 pies.
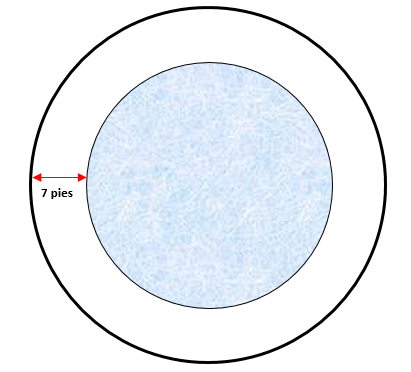
El radio de la verja es igual a la suma del radio de la piscina y la distancia entre los bordes.
{r}_{v}={r}_{p}+7=5+7=12 \mathrm{p}\mathrm{i}\mathrm{e}\mathrm{s}
Sustituimos en la fórmula de perímetro:
{s}_{v}=2\pi {r}_{v}=2\pi \left(12\right)=24\pi \mathrm{p}\mathrm{i}\mathrm{e}\mathrm{s}
Concluimos seleccionando como respuesta correcta la opción D.
Reactivo 44: Volumen de un cilindro
La altura de un cilindro es de 12 metros y su base tiene un diámetro de 10 metros. ¿Cuántos metros cúbicos mide el volumen de este cilindro?
- 60\pi
- 120\pi
- 300\pi
- 360\pi
Solución:
La fórmula para calcular el volumen de un cilindro conocido su diámetro es:
V=\frac{\pi {d}^{2}h}{4}
Donde:
- d es el diámetro
- h es la altura del cilindro
Sustituimos.
V=\frac{\pi {\left(10\right)}^{2}\left(12\right)}{4}=300\pi {m}^{3}
El cilindro tiene un volumen de 300\pi metros cúbicos.
Comparando con las opciones, la respuesta correcta se encuentra en el inciso C.
Reactivo 45: Ángulos en un triángulo
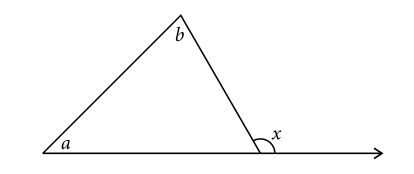
En la figura anterior, m\angle x=
- 180-a
- 180-b
- a+b
- 180\left(a-b\right)
Solución:
En el interior de todo triángulo existen 3 ángulos, en este caso a , b y c que no se indica pero es el suplementario del ángulo externo x .
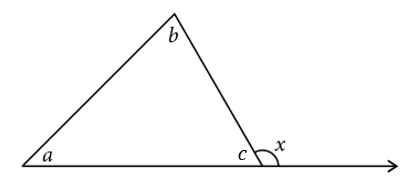
Los tres ángulos internos cumplen la siguiente propiedad:
a+b+c=180
Además, entre c y x se cumple:
c+x=180
Despejamos a c de la anterior expresión y nos queda:
c=180-x
Sustituimos en la primera ecuación:
a+b+180-x=180
Despejamos a x .
a+b-x=0\to x=a+b
Al comparar nuestra respuesta con los incisos, encontramos que la opción correcta es la C.
Reactivo 46: Porcentajes
En una tienda se le aplicó un descuento de 40% al precio P de un artículo. En otra tienda se le aplicó un 50% de descuento al precio Q del mismo artículo. En ambas tiendas el precio final luego de aplicar el descuento fue de $18. ¿Cuál es la diferencia, en dólares, entre los precios P y Q ?
Solución:
El problema indica que, luego de aplicar el descuento a ambos productos sus precios finales son iguales a $18.
P-0.4P=18
Q-0.5Q=18
Podemos despejar de ambas expresiones a P y Q .
P-0.4P=18\to P=\frac{18}{0.6}
Q-0.5Q\to Q=\frac{18}{0.5}
Además, se solicita calcular la diferencia entre los precios originales P y Q .
Diferencia de precios=Q-P
Sustituimos ambas variables y calculamos la diferencia.
Diferencia de precios=\frac{18}{0.5}-\frac{18}{0.6}=36-30=\$6
Reactivo 47: Divisibilidad
El número de cinco dígitos 14K75 es divisible por 3. ¿Cuál es un posible valor de K?
Solución:
Para que un número sea divisible por tres, la suma de sus dígitos debe ser 3 o un múltiplo conocido de 3. Aunque no se indique, K debe ser un número de 1 cifra ya que representa a un dígito de 14K75.
Teniendo en cuenta lo anterior, debemos probar con los números de 0 al 9, sumar los dígitos y comprobar si cumple con el criterio de divisibilidad.
Con el 0 no se cumple, ya que los dígitos 14075 suman 17, el cual es un número primo. Con el 1 la suma de dígitos 14175 es 18, número que es divisible por 3, por tanto K=1 es un valor posible.
Si continuamos con la búsqueda:
K=2\to 14275 no es divisible por 3.
K=3\to 14375 no es divisible por 3.
K=4\to 14475 es divisible por 3.
K=5\to 14575 no es divisible por 3.
K=6\to 14275 no es divisible por 3.
K=7\to 14775 es divisible por 3.
K=8\to 14875 no es divisible por 3.
K=9\to 14975 no es divisible por 3.
Los valores de K posibles son 1, 4 y 7.
Reactivo 48: Probabilidad de eventos aleatorios
Al lanzar 2 dados, ¿Cuál es la probabilidad de que sus 2 caras sumen 5 puntos?
Solución:
Los números que se encuentran en las caras de un dado son: 1, 2, 3, 4, 5 y 6. El total de combinaciones que tenemos al lanzar dos dados es 6*6=36 .
Ahora, las combinaciones que suman 5 son:
{D}_{1}=1, {D}_{2}=4
{D}_{1}=4, {D}_{2}=1
{D}_{1}=2, {D}_{2}=3
{D}_{1}=3, {D}_{2}=2
Es decir, de todo nuestro espacio muestral igual a 36, solo 4 eventos arrojan como resultado que la suma de los puntos es igual a 5. Calculamos la probabilidad P\left({D}_{1}+{D}_{2}=5\right) como el cociente entre los casos favorables sobre el espacio muestral.
P\left({D}_{1}+{D}_{2}=5\right)=\frac{4}{36}=\frac{1}{9}
La probabilidad es de 1/9.
Reactivo 49: Moda de un conjunto de datos
Determine la moda del conjunto de datos \{\mathrm{0,3},10,-\mathrm{3,1},3\} .
Solución:
La moda, es una medida de tendencia central que indica el evento con mayor ocurrencia. Del conjunto de números dado, el que se repite más veces es el 3 por tanto, la moda del espacio muestral es igual a 3.
Reactivo 50: Sistemas de ecuaciones
Cuatro pedazos de pizza y dos refrescos cuestan $7.90. Dos refrescos cuestan 15 centavos más que un pedazo de pizza. ¿Cuánto cuesta, en dólares, un pedazo de pizza?
Solución:
En el enunciado del problema, se establecen diferentes relaciones entre la pizza, el refresco y sus precios. Si P es pizza y R es refresco, de la frase “Cuatro pedazos de pizza y dos refrescos cuestan $7.90” podemos extraer:
4P+2R=7.9
Y de “Dos refrescos cuestan 15 centavos más que un pedazo de pizza”, sabemos que:
2R+0.15=P\to P-2R=-0.15
Tenemos el siguiente sistema de ecuaciones.
4P+2R=7.9
P-2R=-0.15
Como nos interesa solo el costo del pedazo de pizza, podemos sumar ambas ecuaciones para que todo que en función de P .
4P+2R+P-2R=7.9-0.15
Despejamos.
5P=7.75
P=1.55
El pedazo de pizza cuesta $1.55 dólares.
Reactivo 51: Pendiente de la recta
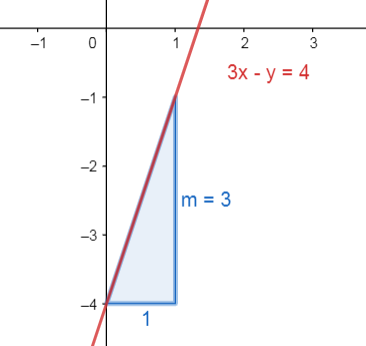
La pendiente de la recta con ecuación 9x-3y=12 es:
Solución:
Para obtener la pendiente de la recta, solo debemos despejar a y , el coeficiente final de la variable x será igual al valor solicitado.
9x-3y=12\to -3y=12-9x
3y=9x-12
y=3x-4
La pendiente de la recta es m=3 .
Reactivo 52: Ecuaciones exponenciales
Si {4}^{n}\times {8}^{n}={2}^{10} , entonces n=
Solución:
Para resolver esta ecuación y encontrar el valor de n , debemos aplicar logaritmo en ambos lados de la ecuación. Puede ser logaritmo de cualquier base, pero en este caso es conveniente hacerlo de base 2.
¿Razón? Todos los números pueden expresarse como potencias de base 2.
{4}^{n}\times {8}^{n}={2}^{10}\to {2}^{2n}\times {2}^{3n}={2}^{10}
Aplicamos logaritmo base 2.
{\mathrm{log}}_{2}\left({2}^{2n}\times {2}^{3n}\right) ={\mathrm{log}}_{2}{2}^{10}
Propiedad del logaritmo de un producto y de una potencia.
{\mathrm{log}}_{2}{2}^{2n} +{\mathrm{log}}_{2}{2}^{3n} ={2}^{10}
2n{\mathrm{log}}_{2}2 +3n{\mathrm{log}}_{2}2 =10{\mathrm{log}}_{2}2
El logaritmo de la base es igual a 1.
2n+3n=10
5n=10
n=2
Concluimos indicando que:
Si {4}^{n}\times {8}^{n}={2}^{10} , entonces n=2 .
Reactivo 53: Ángulos entre rectas
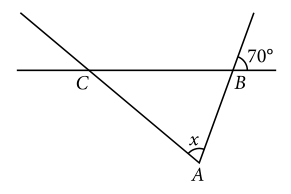
En la figura anterior, AC=BC . ¿Cuál es la medida del ángulo x , en grados?
Solución:
Lo primero que observamos es que, por la propiedad de ángulos opuestos al vértice \widehat{B}=70° . Además, si los segmentos AC y BC son iguales, el ángulo que forman con la recta que corta ambos segmentos es el mismo, el ángulo \widehat{A}=x vale 70°.
Conclusión, la medida del ángulo x es de 70°.
Reactivo 54: Área de figuras relacionadas
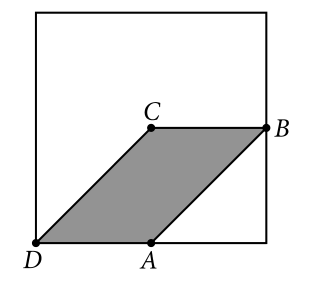
En la figura anterior se muestran un cuadrado y un paralelogramo. Los vértices del paralelogramo son: el centro del cuadrado, los puntos medios de dos de los lados del cuadrado y un vértice de este. Si el área del paralelogramo es 5 centímetros cuadrados, ¿Cuál es el área del cuadrado, en centímetros cuadrados?
Solución:
Recordemos la fórmula para calcular el área de un paralelogramo:
{A}_{p}=bh
En este caso la base corresponde a los segmentos CB=DA y la altura al segmento CA . Debido a que el paralelogramo se encuentra dentro de un cuadrado, es fácil darse cuenta que tanto la altura como la base son iguales a la mitad de un lado del cuadrado.
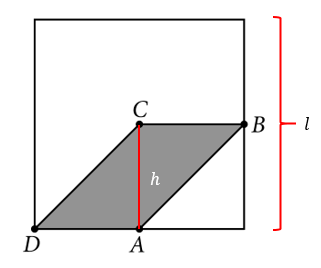
De esta forma:
h=\frac{l}{2}
b=\frac{l}{2}
Sustituyendo en la fórmula de área para un paralelogramo:
{A}_{p}=\frac{l}{2}*\frac{l}{2}=\frac{{l}^{2}}{4}
Por otra parte, el área de un cuadrado se calcula:
{A}_{c}={l}^{2}
Despejamos {l}^{2} de {A}_{c} y sustituimos.
{l}^{2}=4{A}_{p}\to {A}_{c}=4{A}_{p}
{A}_{c}=4\left(5\right)=20 {cm}^{2}
El área del cuadrado es igual a 20 centímetros cuadrados.
Reactivo 55: Volumen de un paralelogramo
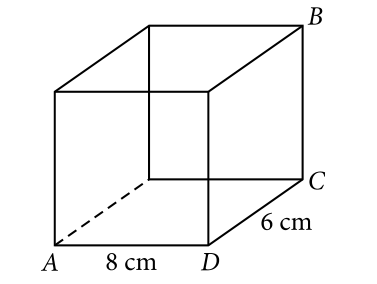
En la figura anterior, BC=\frac{1}{3}CD . ¿Cuántos centímetros cúbicos mide el volumen de la figura?
Solución:
El volumen de un paralelogramo es igual al producto de sus tres dimensiones, en este caso AD , CD y BC .
{V}_{pg}=AD*CD*BC
Sustituimos en la ecuación la relación de BC con el lado CD .
{V}_{pg}=AD*CD*\frac{1}{3}CD=AD*\frac{C{D}^{2}}{3}
Sustituimos ahora los valores numéricos respectivos.
{V}_{pg}=\left(8\right)*\frac{{\left(6\right)}^{2}}{3}=96 {cm}^{3}
La figura tiene un volumen de 96 centímetros cúbicos.

