Hola de nuevo aspirante, en este tutorial vamos a resolver la segunda parte de la guía de ingreso a la UDG en la parte de matemáticas. Vamos a resolver paso a paso los reactivos del 11 al 20, te recomiendo que primero intentes resolverlos por tu cuenta, y después compares tus respuestas y procedimiento.

Matemáticas es solo una de las 4 áreas de estudio de la prueba. Si llegaste hasta aquí y todavía no consultas la primera parte de la guía UDG resuelta de matemáticas, te recomiendo que comiences con la primera parte.
Guía UDG resuelta Parte II
Primero que nada recuerda que la Universidad de Guadalajara aplica la prueba de aptitud académica elaborada por College Board. Si no conoces la estructura del examen puedes consultarla a continuación:
- Lectura (45 reactivos).
- Redacción (25 reactivos).
- Matemáticas (55 reactivos).
- Inglés (50 reactivos).
Comienza a prepararte para el examen de admisión a la UDG con el curso más PRO.
Durante el curso aprenderás todos los temas de la prueba de aptitud académica del College Board.Reactivo 11: Simplificación de potencias
Al simplificar la expresión \frac{{2}^{3}+{3}^{0}}{{3}^{3}-3} se obtiene:
- \frac{7}{24}
- \frac{3}{8}
- \frac{11}{24}
- \frac{8}{9}
Solución:
Para encontrar la forma simplificada de la expresión, debemos resolver cada una de las potencias en el numerador y denominador, aplicando las propiedades de los exponentes, de ser necesario.
Evaluamos {2}^{3} y {3}^{3} .
\frac{{2}^{3}+{3}^{0}}{{3}^{3}-3}=\frac{8+{3}^{0}}{27-3}
Empleamos la propiedad de exponente cero a {3}^{0} .
\frac{8+{3}^{0}}{27-3}=\frac{8+1}{27-3}
Resolvemos sumas y restas.
\frac{8+1}{27-3}=\frac{9}{24}=\frac{3}{8}
Concluimos entonces que:
Al simplificar la expresión \frac{{2}^{3}+{3}^{0}}{{3}^{3}-3} se obtiene \frac{3}{8} .
Comparando con las opciones, seleccionamos al inciso B como la correcta.
Reactivo 12: Probabilidad
En una universidad, 35% de los estudiantes de primer año toma el curso de español, 20% toma el curso de inglés y 10% toma ambos cursos. Si se selecciona al azar uno de los estudiantes de primer año, ¿Cuál es la probabilidad de que NO tome el curso de español ni el de inglés?
- 0.15
- 0.35
- 0.55
- 0.65
Solución:
Una forma de visualizar fácilmente este tipo de problemas, es mediante el uso de diagramas de Venn para conjuntos de datos. En nuestro caso tenemos, principalmente, dos conjuntos: los estudiantes que inscribieron español E y los estudiantes que inscribieron inglés I .
De esta forma, aquellos que inscribieron ambas asignaturas, se representan como la intersección entre los conjuntos I\cap E .
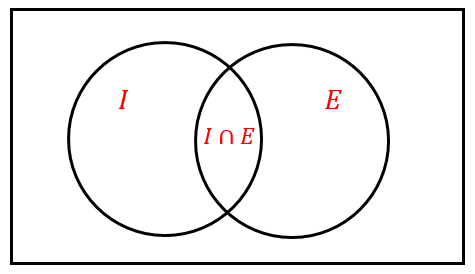
Así, el conjunto de estudiantes que no inscribieron ni inglés ni español, será el complemento de la unión entre los que sí inscribieron español e inglés.
{P}^{\text{'}}=U-{P}_{I\cup E}
Ahora, para calcular {P}_{I\cup E} empleamos la regla aditiva de conjuntos:
{P}_{I\cup E}={P}_{I}+{P}_{E}-{P}_{I\cap E}
Si la totalidad de la población estudiantil es el 100%, las probabilidades {P}_{I}, {P}_{E} e {P}_{I\cap E} son:
{P}_{I}=\frac{20\%}{100\%}=\frac{1}{5}
{P}_{E}=\frac{35\%}{100\%}=\frac{7}{20}
{P}_{I\cap E}=\frac{10\%}{100\%}=\frac{1}{10}
Nos queda que:
{P}_{I\cup E}={P}_{I}+{P}_{E}-{P}_{I\cap E}=\frac{1}{5}+\frac{7}{20}-\frac{1}{10}=\frac{9}{20}
Finalmente, calculamos la probabilidad de escoger a un estudiante que no haya inscrito ninguno de los cursos:
{P}^{\text{'}}=U-{P}_{I\cup E}=1-\frac{9}{20}=\frac{11}{20}=0.55
Comparando el resultado con las opciones de los incisos, seleccionamos como correcta a la opción C.
Reactivo 13: Técnicas de conteo
En la biblioteca de una escuela, tres estudiantes descubrieron que podían colocar tres libros uno al lado del otro de 6 maneras diferentes. ¿De cuántas formas diferentes, en total, se podrían acomodar 4 libros, uno al lado del otro?
- 8
- 10
- 16
- 24
Solución:
En este caso, cada libro representa a un objeto único y diferente, por esta razón cualquier forma en la que se disponen uno al lado de otro será también diferente; porque de una a otra posición los libros se encontrarán en lugares diferentes.
Lo anterior es una manera indirecta para decir que sí importa el orden al contar las formas de acomodar los libros, empleamos la fórmula de permutación.
V=n!
Ya que el número de libros es 4, entonces n=4 .
V=4!=24
Los cuatro libros se pueden acomodar de 24 formas diferentes.
Seleccionamos como respuesta correcta a la opción D.
Reactivo 14: Media aritmética
¿Cuál es el promedio de los factores primos de 105?
- 3
- 5
- 7
- 15
Solución:
Para calcular el promedio solicitado, primero debemos determinar cuáles son los factores primos de 105.
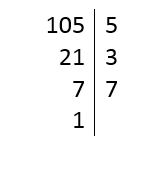
Los factores primos de 105 son: 5, 3 y 7.
Calculamos el promedio como la suma de 5, 3 y 7, dividido la cantidad de factores primos, es decir 3.
\underset{\_}{x}=\frac{5+3+7}{3}=\frac{15}{3}=5
Comparando con las opciones, la respuesta correcta es la B.
Reactivo 15: Probabilidad de un Evento Aleatorio
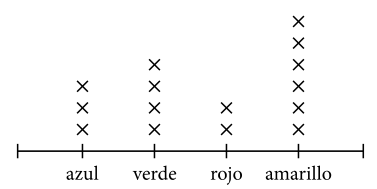
La gráfica anterior representa la distribución de un conjunto de fichas de distintos colores. Si se escoge una de ellas al azar, ¿Cuál es la probabilidad de que esta sea amarilla?
- 0.3
- 0.4
- 0.6
- 0.8
Solución:
Para calcular la probabilidad asociada a cualquier evento, debemos dividir la cantidad de resultados favorables a dicho evento sobre la cantidad total de resultados. De la gráfica de distribución extraemos que:
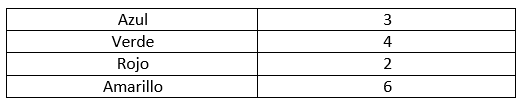
La probabilidad de que sea amarilla es:
P\left(Amarilla\right)=\frac{6}{3+4+2+6}=\frac{6}{15}=0.4
Concluimos seleccionando como respuesta correcta a la opción B.
Reactivo 16: Moda de un conjunto de datos
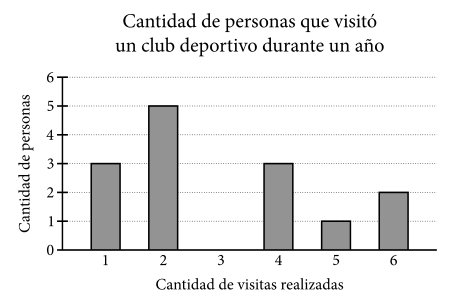
A partir de la gráfica anterior, ¿Cuál es la moda de la cantidad de visitas realizadas al club deportivo?
- 1
- 2
- 3
- 4
Solución:
La moda, es una medida de tendencia central que representa al valor que se manifiesta con mayor frecuencia o en mayores cantidades en un conjunto de datos. En resumen, debemos observar cuál es la cantidad de visitas que más personas tuvo en el club durante un año.
Para los datos de la gráfica, este sería 2 veces, con un total de 5 personas. Concluimos que:
moda=2
Comparando con las opciones, seleccionamos como correcta a la B.
Reactivo 17: Mediana de un conjunto de datos
En la gráfica del reactivo 16, ¿Cuál es la mediana de la cantidad de visitas realizadas al club deportivo?
- 2
- 2.5
- 3
- 3.5
Solución:
La mediana es una medida de tendencia central que separa al conjunto de datos en dos subconjuntos del mismo tamaño. Otra forma de referirse a la mediana es como una medida de localización, ya que representa el valor central de la muestra.
Primero debemos ordenar los datos del gráfico de menor a mayor, repitiendo tantas veces un cierto número de visitas como frecuencia tenga en el gráfico.
1, 1, 1, 2, 2, 2, 2, 2, 4, 4, 4, 5, 6, 6
El total de datos es 14, un número par. La mediana se encuentra entre las posiciones 7 y 8, calculamos el promedio entre ambos valores:
{M}_{e}=\frac{2+2}{2}
{M}_{e}=2
La mediana de los datos es 2.
Comparando con las opciones, escogemos como respuesta correcta la A.
Reactivo 18: Población y muestra estadística
Una compañía de seguros quiere saber la proporción de habitantes de cierta ciudad que tienen sus residencias aseguradas contra accidentes. Para ello, selecciona al azar 100 habitantes de la ciudad y busca la proporción deseada. ¿Cuál es la población del estudio?
- Los habitantes del país
- Los 100 habitantes seleccionados
- Los habitantes de la ciudad con residencia
- Los habitantes de la ciudad con sus residencias aseguradas
Solución:
Para responder esta pregunta, debemos recordar la definición de población. La población es el conjunto total o universo sobre el cual se realiza un experimento o estudio estadístico.
En el enunciado, se habla de conocer la porción de habitantes con residencias aseguradas. Para obtener dicha porción, es necesario emplear algún tipo de instrumento como una encuesta dirigida hacia los habitantes que posean residencia y así determinar cuales la tienen asegurada.
En base al análisis anterior, queda claro que la población de estudio son los habitantes de la ciudad con residencia. Además, aclararemos que los 100 habitantes escogidos al azar son una muestra de esa población de estudio.
Concluimos indicando la opción C como la respuesta correcta.
Reactivo 19: Desviación estándar
En un examen de matemática la media aritmética fue 74 con una desviación estándar de 6. Si la puntuación de un estudiante está 2 desviaciones estándar sobre la media aritmética, ¿Qué puntuación obtuvo este estudiante?
- 86
- 76
- 74
- 62
Solución:
La desviación estándar es un parámetro estadístico que permite estimar que tanto se alejan un conjunto de datos de su media aritmética. El enunciado nos dice cuánto vale la media {x}_{m}=74 , la desviación estándar \sigma =6 y cuánto (por encima) se encuentra la puntuación de un estudiante: 2 \sigma .
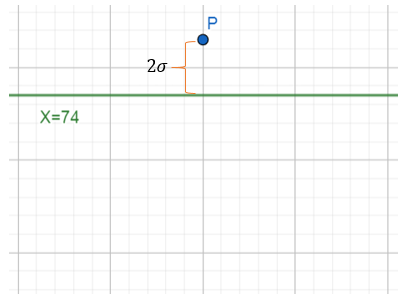
Por tanto, la puntuación será la media sumado a 2\sigma .
P=74+2\sigma =74+12=86
Comparando con las opciones del problema, seleccionamos como correcta la A.
Reactivo 20: Gráfico de tallo y hoja

En la figura anterior se muestra un diagrama de tallo y hoja de las puntuaciones de una prueba de un máximo de 60 puntos para calificar para un trabajo. ¿Cuántos tienen la oportunidad de ser seleccionados si se requiere aprobar un 70% de la prueba?
- 5
- 8
- 11
- 13
Solución:
Un gráfico de tallo y hoja permite representar un conjunto de datos cuyas cifras a la izquierda se repiten más de una vez. La cifra a la izquierda representará al tallo y el resto a la derecha las hojas.
De esta forma, en el gráfico podemos identificar 6 calificaciones entre con cifra significativa 1, 5 con cifra significativa 2 y así sucesivamente.
La máxima puntuación que se puede obtener en la prueba es 60 y se aprueba con el 70%, es decir 42 puntos. Debemos identificar en el gráfico las calificaciones mayores o iguales a 42, esto nos permite descartar los tallos con 3, 2 y 1.
En el tallo con 4 hay 6 participantes con calificación mayor a 42 y en el tallo con 5 todos califican. El total de aspirantes preseleccionados es 11.

Concluimos seleccionando a la opción C como la respuesta correcta al problema.

