En este tutorial vamos a resolver la tercera parte de la guía UDG de matemáticas correspondiente a la prueba de aptitud académica de College Board para el examen de ingreso a la UDG.

En este punto ya debiste resolver los primeros 20 reactivos de la guía de UDG correspondientes al área de matemáticas. Si no es así, te recomiendo primero intentar resolver los ejercicios por tu cuenta, y después consultar tus respuestas y procedimiento.
Guía UDG resuelta Parte III
La Universidad de Guadalajara aplica la prueba de aptitud académica elaborada por College Board. La estructura del examen de ingreso a la UDG es la siguiente:
- Lectura (45 reactivos).
- Redacción (25 reactivos).
- Matemáticas (55 reactivos).
- Inglés (50 reactivos).
Comienza a prepararte para el examen de admisión a la UDG con el curso más PRO.
Durante el curso aprenderás todos los temas de la prueba de aptitud académica del College Board.Vamos a comenzar con la solución de los reactivos del 21 al 30, recuerda que no basta con hacerlo bien, también tienes que hacerlo lo más rápido posible.
Reactivo 21: Despeje de ecuaciones
¿Cuál de las siguientes opciones es una solución de la ecuación 4{x}^{2}-8=56 ?
- 4
- 8
- 16
- 32
Solución:
Comenzamos dividiendo ambos miembros entre 4 para simplificar los coeficientes.
4{x}^{2}-8=56\to {x}^{2}-2=14
Pasamos a sumar el 2 hacia el segundo miembro.
{x}^{2}-2=14\to {x}^{2}=16
Aplicamos raíz cuadrada en ambos miembros.
{x}^{2}=16\to x=\pm \sqrt{16}
x=\pm 4
Las soluciones de la ecuación son +4 y -4.
Comparando con las opciones, seleccionamos como correcta la A.
Reactivo 22: Plano cartesiano
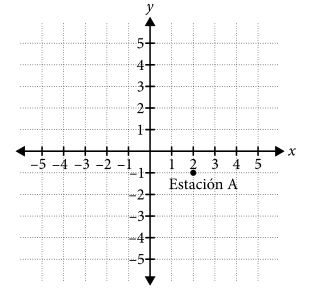
Mateo comienza una caminata en la estación A , cuya localización se muestra en la figura anterior. Luego se mueve a la estación B que está 3 kilómetros al norte. Para completar su caminata se mueve 5 kilómetros al oeste donde está la estación C . ¿Cuáles son las coordenadas de Mateo al fin de la caminata?
- \left(\mathrm{2,2}\right)
- \left(\mathrm{3,2}\right)
- \left(-\mathrm{3,2}\right)
- \left(3,-2\right)
Solución:
Para encontrar las coordenadas finales de Mateo, trazaremos uno a uno los desplazamientos que va dando en la figura dada por el problema.
Desplazamiento 1: … se mueve 3 kilómetros al norte. Recordemos, el norte es hacia arriba por lo tanto:
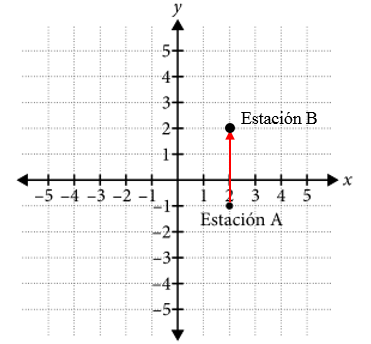
Desplazamiento 2: … se mueve 5 kilómetros al oeste. El oeste queda a la izquierda, por tanto Mateo se desplaza 5 kilómetros a la izquierda.
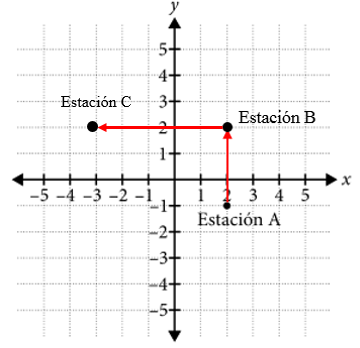
Las coordenadas de Mateo al finalizar su caminata son \left(-\mathrm{3,2}\right) .
Concluimos el problema seleccionando como correcta a la opción C.
Reactivo 23: Lenguaje natural y algebraico
La frase “cinco menos el doble de un número p ” se traduce algebraicamente como:
- 5-{p}^{2}
- 2p-5
- {p}^{2}-5
- 5-2p
Solución:
Como en todos los problemas de lenguaje natural a algebraico y viceversa, debemos examinar detenidamente cada parte de la frase para encontrar la expresión correcta.
El inicio, cinco menos… es equivalente a -5. Dicho de otra manera, indica que a lo que viene se le restan 5 unidades. Ahora el doble de un número p , es equivalente a 2p y es la expresión a la que se le restaron 5.
En ecuación matemática todo quedaría como:
2p-5
Concluimos escogiendo como opción correcta la B.
Reactivo 24: Dominio de funciones reales
El dominio de la función f\left(x\right)=2+\sqrt{x-1} es:
- [0,\infty )
- [-1,\infty )
- [1,\infty )
- [2,\infty )
Solución:
Para estudiar el dominio de una función constituida por varios términos que se suman y restan, debemos encontrar el dominio de cada término y finalmente interceptarlos, el resultado será el dominio de la función original.
En este caso la función está compuesta de 2 términos: uno independiente cuyo dominio son todos los reales y un radical.
Dominio del término radical.
\sqrt{x-1}
Para que el resultado dado por una expresión radical se mantenga en los reales, el radicando debe ser mayor o igual que cero.
x-1\ge 0
Despejamos.
x\ge 1
Expresado como intervalo:
Dom\left\{\sqrt{x-1}\right\}=x\in [1,\infty )
Al intersectar el dominio del radical con el del término independiente, el resultado es el mismo dominio que el radical, por tanto:
Dom\left\{2+\sqrt{x-1}\right\}=x\in [1,\infty )
Comparando nuestro resultado con las opciones, seleccionamos como correcta a la del inciso C.
Reactivo 25: Evaluando funciones
Si f\left(x\right)=3{x}^{2}+2x-4 , ¿Cuánto es f\left(3\right) ?
- 16
- 20
- 25
- 29
Solución:
Para evaluar una función en un punto, debemos antes estar seguros que dicho valor de x pertenezca al dominio de f . Debido a que es una función polinómica, su dominio son todos los reales, por lo que podemos sustituir x=3 sin cuidado.
Ahora, en los lugares donde está la x colocamos el 3 entre paréntesis.
f\left(3\right)=3{\left(3\right)}^{2}+2\left(3\right)-4
Resolvemos potencias, luego productos y de último sumas y restas.
f\left(3\right)=3\left(9\right)+2\left(3\right)-4=27+6-4=29
El resultado de evaluar f\left(3\right) es 29.
Escogemos como respuesta correcta a la opción D.
Reactivo 26: Recta numérica e inecuaciones

La figura anterior muestra la solución gráfica de
- x+2>0
- x+2<0
- x-2<0
- x-2>0
Solución:
Comencemos por representar en forma de desigualdad el conjunto representado en la figura, para luego llegar a la inecuación original aplicando ciertas operaciones. El conjunto representa a los valores de x que son mayores que 2.
x>2
Restamos 2 a ambos lados.
x-2>2-2
x-2>0
La inecuación que tiene como solución gráfica a la figura es: x-2>0
Comparando con las opciones, la respuesta correcta es la D.
Reactivo 27: Problemas matemáticos
Norma lee un libro de la siguiente manera: el primer día lee las primeras 5 páginas y en cada uno de los siguientes días lee 3 páginas solamente. ¿Cuántos días se requieren para que Norma lea un libro que contiene 100 páginas?
- 34
- 33
- 32
- 31
Solución:
Ya que Norma lee el primer día 5 páginas, de un libro con 100 páginas le quedan 95 para el resto de días. Ahora, a partir del segundo día leerá 3 páginas hasta acabar el libro entonces, los días totales se calculan como:
Días de lectura=1+\frac{95}{3}=1+31.6
Ya que los días cuentan enteros, podemos redondear 31.6 a 32.
Días de lectura=1+32=33
Norma tardará 33 días en leer un libro de 100 páginas.
Comparando con las opciones, seleccionamos como correcta a la B.
Reactivo 28: Operaciones algebraicas
Si 4x=\frac{5}{6}y , entonces 5y es igual a:
- \frac{1}{2}x
- \frac{4}{6}x
- 20x
- 24x
Solución:
Para eliminar el 6 del denominador de la fracción que es factor de la y , podemos multiplicar ambos lados por 6.
6*4x=6*\frac{5}{6}y
Simplificamos.
24x=5y
Concluimos entonces que 5y es igual a 24x .
Comparando con las opciones, la respuesta correcta es la D.
Reactivo 29: Regla de 3 inversa
Suponga que x y w varían inversamente, esto es, el producto entre x y w es constante. Además, cuando w=6 , entonces x=4 . ¿Cuánto es el valor de w cuando x=8 ?
- \frac{1}{3}
- \frac{3}{4}
- 3
- 24
Solución:
Para encontrar el valor de w , debemos aplicar una relación inversa entre ambas variables.
Cuando x=4\to w=6
Si x=8\to w=?
w=\frac{\left(4\right)\left(6\right)}{8}=\frac{24}{8}=3
Si x=8 entonces w disminuye a 3.
Seleccionamos como correcta la opción C.
Reactivo 30: Problemas con Sistemas de Ecuaciones
En una elección votaron 1.5 millones de electores por dos candidatos. El candidato II recibió 15,000 votos más que el candidato I. ¿Cuántos votos recibió el Candidato I?
- 1,515,000
- 1,485,000
- 757,500
- 742,500
Solución:
Para calcular la cantidad de electores que votaron por el Candidato I, debemos establecer un sistema de ecuaciones con la información suministrada por el enunciado.
Ya que la población total de votantes fue de 1,500,000 esa es la cantidad de votos que han recibido juntos ambos candidatos.
CI+CII=1500000
Además, el Candidato II recibió 15,000 más que el Candidato I, esto puede expresarse como:
CII=CI+15000
Podemos sustituir a CII en la primera ecuación para calcular directamente los votantes que ha recibido CI .
CI+CI+15000=1500000
Despejamos.
2CI=1500000-15000
CI=\frac{1485000}{2}=742500
El Candidato I recibió 742,500 votos.
Este resultado corresponde al inciso D.

