Llegamos a la séptima parte de la guía de ingreso resuelta con los reactivos del 73 al 83 para las divisiones de CBI y CNI del examen ingreso a la Universidad Autónoma Metropolitana. Puedes acceder al resto de partes a través de los botones de navegación.

Guía UAM Matemáticas Parte 7 resuelta
¡Felicidades aspirante! esta es la última parte de la guía resuelta de matemáticas para la UAM en las divisiones de Ciencias Básicas e Ingeniería y Ciencias Naturales e Ingeniería.
Esta guía es una parte del contenido que tenemos en Unibetas Pro para ti. No olvides visitar el canal de youtube, donde podrás interactuar con los profes en nuestros lives, acceder a guías resueltas y contenido valioso para tu preparación.
Reactivo 73: Identidades trigonométricas
Elige la opción que completa la identidad trigonométrica
\cos (a+b)=\cos a\_\_\_\_-\operatorname{sen} b\_\_\_\_.
- \sin (a-b), \cos (a-b)
- \cos (b-a), \sin (a-b)
- \sin a, \cos b
- \cos (a-b), \sin (a-b)
- \cos b, \sin a
Solución:
A partir de las identidades trigonométricas básicas, el coseno de la suma de ángulos es:
\cos (a+b)=\cos (a) \cos (b)-\sin (a) \sin (b)
Por tanto, en el enunciado falta cos \left(b\right) en el primer término y \left(a\right) en el segundo. Concluimos indicando que:
\cos (a+b)=\cos a \cos b-\operatorname{sen} b \operatorname{sen} a
La respuesta correcta es la E \cos b, \sin a .
Reactivo 74: Ley de senos
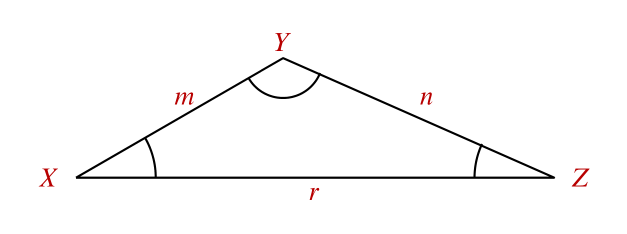
La ecuación que determina el valor de n en la figura es __________.
- \frac{n}{\operatorname{sen} Z}=\frac{m}{\operatorname{sen} X}
- \frac{r}{\operatorname{sen} Y}=\frac{n}{\operatorname{sen} X}
- \frac{m}{\operatorname{sen} Z}=\frac{n}{\operatorname{sen} Y}
- \frac{r}{\operatorname{sen} X}=\frac{n}{\operatorname{sen} Z}
- \frac{r}{\operatorname{sen} Z}=\frac{n}{\operatorname{sen} Y}
Solución:
La ley de los Senos indica que la relación entre un lado del triángulo y el seno del ángulo opuesto al mismo es una constante y es igual para los tres pares ángulo/lado opuesto del triángulo. Tomando como base al triángulo dado, las relaciones quedarían:
\frac{m}{\sin Z}=\frac{n}{\sin X}=\frac{r}{\sin Y}
Suponiendo que conocemos a todos los elementos exceptuando n , al mismo lo podríamos calcular como:
\frac{m}{\sin Z}=\frac{n}{\sin X}
O también:
\frac{n}{\sin X}=\frac{r}{\sin Y}
Comparando estas opciones con lo mostrado en cada inciso, el único que muestra una forma correcta de calcular a n es B, razón por la que se escoge como respuesta correcta.
La ecuación que determina el valor de n en la figura es \frac{n}{\sin X }=\frac{r}{\sin Y } .
Reactivo 75: Racionalización
Al racionalizar \frac{\sqrt{2x+h}-\sqrt{2x}}{h} , se obtiene __________.
- \frac{h}{\sqrt{2x+h}+\sqrt{2x}}
- \frac{1}{\sqrt{2x+h}-\sqrt{2x}}
- \frac{h}{\sqrt{2x+h}-\sqrt{2x}}
- \frac{1}{\sqrt{4x+h}}
- \frac{1}{\sqrt{2x+h}+\sqrt{2x}}
Solución:
Ya que los términos son raíces cuadradas, podemos deshacernos de las mismas si multiplicamos y dividimos a la fracción por su conjugado, es decir un binomio con los mismos términos pero con el signo cambiado; en este caso positivo.
Recordemos que:
\left(\sqrt{q}-\sqrt{p}\right)\left(\sqrt{q}+\sqrt{p}\right)={\left(\sqrt{q}\right)}^{2}-{\left(\sqrt{p}\right)}^{2}=q-p
El conjugado sería:
\sqrt{2x+h}+\sqrt{2x}
Multiplicando y dividiendo queda:
\frac{\sqrt{2x+h}-\sqrt{2x}}{h}\bullet \frac{\sqrt{2x+h}+\sqrt{2x}}{\sqrt{2x+h}+\sqrt{2x}}
Desarrollamos
\frac{\left(\sqrt{2x+h}-\sqrt{2x}\right)\left(\sqrt{2x+h}+\sqrt{2x}\right)}{h\left(\sqrt{2x+h}+\sqrt{2x}\right)}=\frac{2x+h-2x}{h\left(\sqrt{2x+h}+\sqrt{2x}\right)}=\frac{h}{h\left(\sqrt{2x+h}+\sqrt{2x}\right)}
\therefore \frac{h}{h\left(\sqrt{2x+h}+\sqrt{2x}\right)}=\frac{1}{\sqrt{2x+h}+\sqrt{2x}}
Concluimos que:
Al racionalizar \frac{\sqrt{2x+h}-\sqrt{2x}}{h} , se obtiene \frac{1}{\sqrt{2x+h}+\sqrt{2x}} .
Comparando este resultado con las opciones, escogemos como correcta a la E.
Reactivo 76: Segmento dividido una razón
Considera el segmento de recta cuyos extremos son los puntos E(-2,-1),G\left(\mathrm{3,9}\right) ¿Cuáles son las coordenadas del punto P que divide el segmento EG en la razón \frac{1}{3} ?
- P\left(\frac{1}{2},4\right)
- P\left(-\frac{5}{3},-\frac{10}{3}\right)
- P\left(\frac{1}{3},\frac{8}{3}\right)
- P\left(-\frac{3}{4},\frac{3}{2}\right)
- P\left(-\frac{5}{2},-5\right)
Solución:
La razón en la que es dividido el segmento EG por el punto P se expresa como:
r=\frac{EP}{PG}=\frac{1}{3}
Es decir, el punto P es más cercano al extremo E del segmento debido a que la razón es menor que uno y mayor que cero. Teniendo esto en cuenta, las ecuaciones para calcular las coordenadas de P son:
{x}_{p}=\frac{{x}_{e}+r{x}_{g}}{1+r}
{y}_{p}=\frac{{y}_{e}+r{y}_{g}}{1+r}
Sustituimos las coordenadas de los extremos y el valor de la razón.
{x}_{p}=\frac{-2+\left(\frac{1}{3}\right)\left(3\right)}{1+\frac{1}{3}}=-\frac{3}{4}
{y}_{p}=\frac{-1+\left(\frac{1}{3}\right)\left(9\right)}{1+\frac{1}{3}}=\frac{3}{2}
Concluimos que:
P\left(-\frac{3}{4},\frac{3}{2}\right)
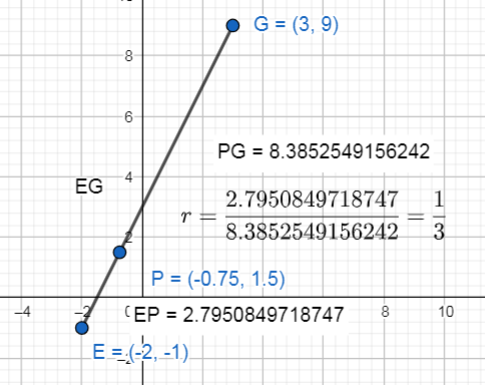
Escogemos como respuesta correcta a la opción D.
Reactivo 77: Posición relativa entre rectas
De las siguientes ecuaciones, selecciona aquellas que son rectas paralelas entre sí.
- y=\frac{5}{3}x+1
- y=\frac{3}{5}x+2
- y=-\frac{3}{5}x+3
- y=\frac{5}{3}x+4
- y=-\frac{5}{3}x+4
- 2 y 5
- 2 y 3
- 3 y 4
- 1 y 4
- 1 y 2
Solución:
De los temas referentes a la geometría analítica, sabemos que una condición necesaria y suficiente para que dos rectas sean paralelas, es que sus pendientes sean iguales. Por tanto, este problema se resume en identificar cuál es el par de rectas que poseen la misma pendiente.
Recordemos que las rectas están en su forma punto-pendiente por tanto, la pendiente se obtiene al inspeccionar el coeficiente que acompaña a la x .
y=mx+b
Las rectas de los incisos 1 y 4 poseen la misma pendiente:
y=\frac{5}{3}x+1
y=\frac{5}{3}x+4
Concluimos el problema seleccionando como respuesta correcta a la opción D.
Reactivo 78: Corte con los ejes
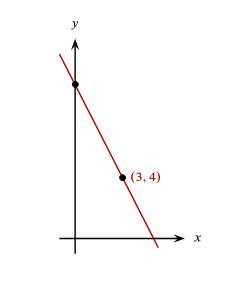
Si la pendiente de la recta mostrada en la figura es -2 ¿Cuánto vale su ordenada en el origen?
- 7
- 3
- 11
- 10
- 4
Solución:
El ejercicio nos pide calcular el corte con el eje y de la recta mostrada en la figura. Para ello, tenemos como dato la pendiente m=-2 y un punto que pertenece a la recta \left(\mathrm{3,4}\right) . Recurriremos a la ecuación punto-pendiente para sustituir estos valores y despejar a b .
y=mx+b
Sustituimos.
4=\left(-2\right)\left(3\right)+b\to 4=-6+b
b=4+6=10
La recta corta con las ordenadas en y=10 .
Comparando con las opciones, escogemos como respuesta correcta a la D.
Reactivo 79: Intersección entre rectas
Determinar el punto de intersección de las rectas, cuyas ecuaciones son:
3x-2y=-11
2x+y=2
- \left(-\mathrm{1,4}\right)
- \left(3,-1\right)
- \left(\mathrm{1,4}\right)
- \left(4,-1\right)
- \left(-\mathrm{3,1}\right)
Solución:
Para calcular el punto de intersección entre las rectas, debemos resolver el sistema de ecuaciones que estas forman. Podemos recurrir a cualquier método, en este caso lo haremos por sustitución.
\left\{\begin{array}{c} 3 x-2 y=-11 \\ 2 x+y=2 \end{array}\right.
Despejamos a y de la segunda ecuación y sustituimos la expresión obtenida en la primera.
2x+y=2\to y=2-2x
Sustituimos en 1.
3x-2\left(2-2x\right)=-11
3x-4+4x=-11
7x=4-11
x=-1
Ahora, sustituimos x=-1 en cualquiera de las dos ecuaciones para obtener la ordenada del punto de intersección.
y=2-2x\to y=2-2\left(-1\right)=4
Punto de intersección:
P\left(\mathrm{1,4}\right)
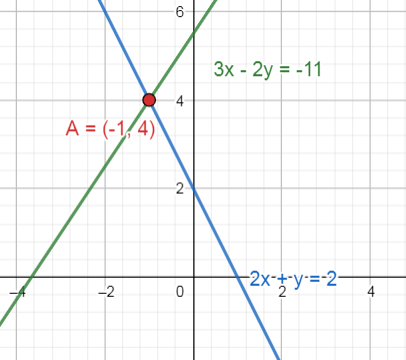
Comparando con las opciones, seleccionamos como respuesta correcta a la A.
Reactivo 80: La elipse
Si los focos de una elipse son los puntos \left(3, 8\right) y \left(3, 2\right) , y la longitud de su eje menor es 8, la ecuación de la elipse es ___________.
- \frac{(x-3{)}^{2}}{16}-\frac{(y-5{)}^{2}}{9}=1
- \frac{(x-3{)}^{2}}{25}+\frac{(y-5{)}^{2}}{16}=1
- \frac{(x-3{)}^{2}}{16}+\frac{(y-5{)}^{2}}{25}=1
- \frac{(x-3{)}^{2}}{9}-\frac{(y-5{)}^{2}}{16}=1
- \frac{(x+3{)}^{2}}{16}-\frac{(y+5{)}^{2}}{9}=1
Solución:
Lo primero que podemos identificar observando las coordenadas de los focos, es que ambos tienen igual coordenada en x pero distingue coordenada y , eso significa que la elipse tiene su eje mayor paralelo al eje y .
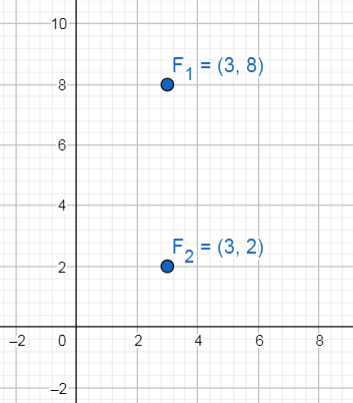
Además, la magnitud del eje menor es 8 . Recordemos que a es la mitad de la longitud del eje mayor y b la mitad de la longitud del eje menor. Por otra parte, tenemos la siguiente relación:
{c}^{2}={a}^{2}-{b}^{2}
Donde c es la mitad de la distancia focal, en este caso {F}_{1}{F}_{2}=6 por tanto c=3 . Despejamos a a de la ecuación anterior:
a=\sqrt{{c}^{2}+{b}^{2}}\to a=\sqrt{{\left(3\right)}^{2}+{\left(4\right)}^{2}}
\therefore a=5
Las coordenadas del centro se obtienen al determinar el punto medio entre los focos:
C\left(3,\frac{8+2}{2}\right)=C\left(\mathrm{3,5}\right)
Para armar la ecuación ordinaria de la elipse, el parámetro a se coloca en la fracción de la y (ya que el eje mayor es paralelo a las ordenadas) y el parámetro b en la fracción de las x .
Ecuación de la elipse.
\frac{{\left(x-h\right)}^{2}}{{b}^{2}}+\frac{{\left(y-k\right)}^{2}}{{a}^{2}}=1
Sustituimos los parámetros.
\frac{{\left(x-3\right)}^{2}}{{4}^{2}}+\frac{{\left(y-5\right)}^{2}}{{5}^{2}}=1
\frac{{\left(x-3\right)}^{2}}{16}+\frac{{\left(y-5\right)}^{2}}{25}=1
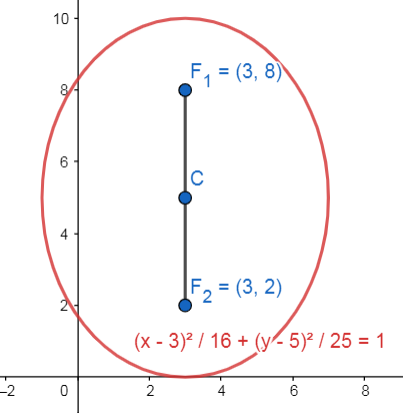
Comparando con las opciones, escogemos como correcta a la C.
Reactivo 81: La hipérbola
¿Cuál es la ecuación de la hipérbola de la siguiente gráfica?
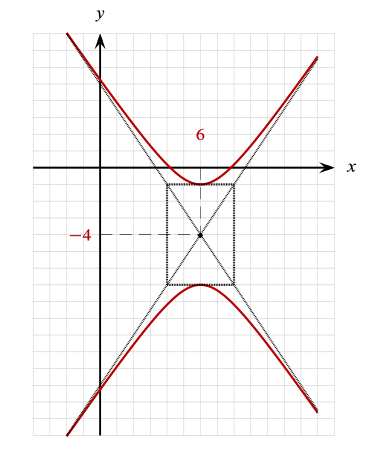
- \frac{(x-6{)}^{2}}{9}-\frac{(y+4{)}^{2}}{4}=1
- -\frac{(x+4{)}^{2}}{9}+\frac{(y-6{)}^{2}}{4}=1
- -\frac{(x-6{)}^{2}}{4}+\frac{(y+4{)}^{2}}{9}=1
- \frac{(x+4{)}^{2}}{4}+\frac{(y-6{)}^{2}}{9}=1
- -\frac{(x-6{)}^{2}}{9}+\frac{(y+4{)}^{2}}{4}=1
Solución:
La ecuación ordinaria de una hipérbola con eje focal paralelo al eje y (tal como la que se muestra en la figura) es:
\frac{(y-k{)}^{2}}{{a}^{2}}-\frac{(x-h{)}^{2}}{{b}^{2}}=1
Donde h, k son las coordenadas del centro y los parámetros a, b las magnitudes del eje mayor y menor respectivamente. Todas estas magnitudes pueden extraerse de la figura adjunta. Con un primer vistazo, nos damos cuenta que el centro es C\left(6, -4\right) .
Por otro lado a y b se obtienen del rectángulo punteado. a es la mitad de la arista más larga y b la mitad de la más corta.
a=3;b=2
Sustituyendo el centro, a y b queda:
\frac{(y+4{)}^{2}}{{3}^{2}}-\frac{(x-6{)}^{2}}{{2}^{2}}=1
\frac{(y+4{)}^{2}}{9}-\frac{(x-6{)}^{2}}{4}=1\to -\frac{(x-6{)}^{2}}{4}+\frac{(y+4{)}^{2}}{9}=1
Comparando con las opciones, la respuesta correcta es la C.
Reactivo 82: Ecuación de la recta
Determinar la ecuación de la recta que pasa por el punto P\left(3, -1\right) y es perpendicular a la recta:
3x+2y-4=0.
- 3x+2y-7=0
- 2x-3y-9=0
- 3x+2y+11=0
- 2x-3y-5=0
- 2x+3y+5=0
Solución:
Una condición suficiente y necesaria para que dos rectas sean perpendiculares, es que sus pendientes tienen la siguiente relación:
{m}_{2}=-\frac{1}{{m}_{2}}
La pendiente {m}_{1} se puede extraer de la ecuación de recta dada.
3x+2y-4=0\to y=2-\frac{3}{2}x
Entonces:
{m}_{1}=-\frac{3}{2}
Sustituyendo en la relación:
{m}_{2}=-\frac{1}{-\frac{3}{2}}=\frac{2}{3}
Con la pendiente y un punto que pertenece a la recta, podemos sustituirla en la ecuación punto-pendiente y encontrar la respuesta al problema.
y-{y}_{o}=m\left(x-{x}_{o}\right)
Sustituimos.
y+1=\frac{2}{3}\left(x-3\right)
Desarrollamos.
y+1=\frac{2}{3}x-2
Simplificamos.
3y+3=2x-6
-2x+3y+9=0
2x-3y-9=0
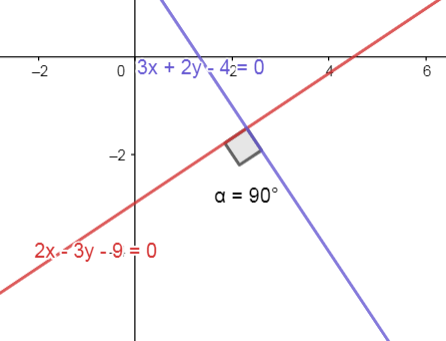
Comparando con los incisos, seleccionamos como correcta a la opción B.
Reactivo 83: Derivada con fórmula
La derivada con respecto a x de la función y=(3x+1{)}^{2} es ___________.
- 3x+1
- 6x+2
- 3x+2
- 6x+3
- 18x+6
Solución:
Para encontrar la derivada de esta función debemos identificar la fórmula o propiedad de la derivada que hay que aplicar. En este caso, es una potencia con exponente 2 y base igual a 3x+1 , recurrimos a la fórmula de la derivada de una potencia.
\frac{df{\left(x\right)}^{n}}{dx}=nf{\left(x\right)}^{\text{'}}f{\left(x\right)}^{n-1}
Comparando con la función dada identificamos que:
n=2
f\left(x\right)=3x+1
Calculamos la derivada.
\frac{d\left({\left[3x+1\right]}^{2}\right)}{dx}=2{\left(3x+1\right)}^{\text{'}}\left(3x+1\right)
Resolvemos la derivada faltante. Aplicamos la fórmula de la derivada de x y la derivada de una constante.
\frac{d\left({\left[3x+1\right]}^{2}\right)}{dx}=2\left(3\right)\left(3x+1\right)
Simplificamos.
\frac{d\left({\left[3x+1\right]}^{2}\right)}{dx}=2\left(3\right)\left(3x+1\right)=6\left(3x+1\right)
\frac{d\left({\left[3x+1\right]}^{2}\right)}{dx}=18x+6
Finalmente:
La derivada con respecto a x de la función y=(3x+1{)}^{2} es 18x+6 .
Comparando con las opciones que ofrece el problema, seleccionamos como correcta a la E.

