¡Hola aspirante! En esta primera parte vamos a resolver los reactivos del 13 al 22 de la guía de matemáticas para la división de Ciencias Básicas e Ingeniería de la Universidad Autónoma Metropolitana (UAM).

¡Recuerda! Si aún no los resuelves por tu cuenta, te invito a que lo intentes y luego regreses. Es importante que domines los temas que van para las dos partes del examen.
Antes de continuar con el resto del tutorial, te dejo un resumen de la convocatoria con datos cruciales que no debes pasar por alto.
- Número de convocatorias: Dos al año.
- Fechas de registro: marzo y agosto del 2022
- Oferta académica: 82 carreras
- Divisiones académicas: 6
- Modalidad: en línea
Estructura del examen de ingreso UAM 2022
El examen de ingreso a la UAM, está dividida en dos partes: una prueba de aptitudes académicas y otra de conocimientos específicos que dependerá de la carrera a la que desees ingresar.
A grandes rasgos, la prueba de aptitudes se divide en dos ramas, cada una con 20 reactivos.
- Prueba de razonamiento verbal
- Prueba de razonamiento matemático.
Esta parte del examen se mantiene para las 6 divisiones en la UAM, lo único que cambiará será la selección de los temas en la parte de Razonamiento Matemático.
En el caso de Ciencias Básicas e Ingeniería (CBI) y Ciencias Naturales e Ingeniería (CNI), la segunda parte consta de tres asignaturas junto con Razonamiento simbólico-abstracto y Razonamiento Lógico.
Los conocimientos específicos cambian según de la división de la carrera a la que deseas ingresar.
Matemáticas
- Aritmética
- Álgebra
- Racionalización
- Geometría euclidiana
- Trigonometría plana
- Geometría analítica
- Cálculo diferencial e integral
Física
- Análisis dimensional
- Cinemática
- Dinámica
- Estática
- Hidrostática
- Electrostática
Química
- Materia
- Estructura del átomo
- Nomenclatura
- Reacciones químicas
En la siguiente tabla encontrarás un resumen de la estructura del examen.
| Área | Reactivos | Porcentaje |
|---|---|---|
| Razonamiento verbal | 20 | 25% |
| Razonamiento matemático | 20 | 25% |
| Conocimientos específicos | 40 | 50% |
| Total | 80 | 100% |
Temario de Matemáticas para CBI y CNI
El temario puede parecer extenso, pero al iniciar tu preparación con antelación, podrás dominarlos a la perfección. Te recomiendo no saltar ningún detalle, date el tiempo que necesites con cada tema hasta comprenderlo.
Aritmética
- Mínimo común múltiplo y máximo común divisor
- Operaciones con fracciones numéricas
Álgebra
- Valor numérico de expresiones algebraicas
- Términos semejantes
- Uso de paréntesis
- Leyes de los exponentes y radicales
- Operaciones con polinomios
- Productos notables
- Factorización
- Operaciones con fracciones algebraicas
Racionalización
- Ecuaciones de primer grado con una incógnita
- Sistemas de ecuaciones lineales
- Ecuaciones de segundo grado
Geometría euclidiana
- Ángulos complementarios y suplementarios
- Ángulos formados al cortar dos paralelas por una transversal
- Propiedades de paralelogramos y triángulos
- Triángulos congruentes y semejantes
- Teorema de Pitágoras
- Perímetro y área de polígonos, y del círculo
- Área y volumen de paralelepípedos, cilindros, conos y esferas
Trigonometría plana
- Medida de ángulos en grados y radianes
- Funciones trigonométricas de ángulos notables
- Identidades trigonométricas básicas
- Resolución de triángulos rectángulos
- Funciones de la adición de ángulos
- Funciones de la sustracción de ángulos
- Ley de los cosenos
- Ley de los senos
- Resolución de triángulos oblicuángulos
Geometría analítica
- Distancia entre dos puntos
- División de un segmento en una razón dada. Punto medio
- Ángulo de inclinación y pendiente de una recta
- Condiciones de paralelismo y perpendicularidad
- Ecuación de la recta en todas sus formas
- Intersección de rectas
- Ecuación y elementos principales de la circunferencia
- Ecuación y elementos principales de la parábola
- Ecuación y elementos principales de la elipse
- Ecuación y elementos principales de la hipérbola
Cálculo diferencial e integral
- Derivadas de sumas, productos, cocientes y potencias de funciones
- Integrales inmediatas
En el examen real, los reactivos de cada tema se escogen al azar. No te confíes y estudia cada parte por igual.
Guía UAM de Matemáticas resuelta
Vamos finalmente a resolver, paso a paso, los primeros 10 reactivos de matemáticas para la Guía de Ciencias Básicas e Ingeniería, que aplica igualmente a la división de Ciencias Naturales e Ingeniería.
Reactivo 13: Modelado matemático
Una ventana rectangular tiene l metros de ancho y h metros de altura, con un perímetro de 6 m y un área de 2 {m}^{2} ¿Con cuál de las siguientes ecuaciones se puede calcular el ancho de la ventana?
- {l}^{2}-3l+2=0
- {l}^{2}+3l+2=0
- {l}^{2}-6l+2=0
- {l}^{2}+6l+2=0
- {l}^{2}+3l-2=0
Solución:
Para encontrar la ecuación que permite calcular el ancho de la ventana, necesitamos armar un sistema de ecuaciones con las expresiones de perímetro y área, ambas en función de la altura y el ancho de la misma.
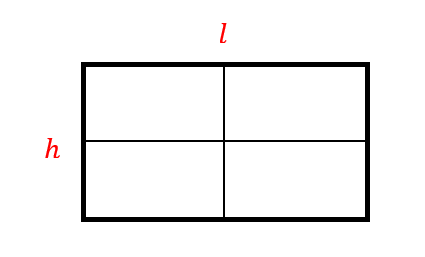
El perímetro de una figura plana se calcula sumando la magnitud de sus lados. Como la ventana es rectangular dos lados miden l y los otros dos h por tanto:
2l+2h=6 m
Además, el área de un rectángulo se obtiene al multiplicar el alto por el ancho, es decir:
l\bullet h=2 {m}^{2}
De esta forma, obtenemos un sistema de dos ecuaciones con dos incógnitas:
\left\{\begin{array}{c} 2 l+2 h=6 \\ l \cdot h=2 \end{array}\right.
Aplicamos el método por sustitución, despejando de la segunda ecuación la altura de la ventana para luego sustituirlo en la primera ecuación.
l\bullet h=2\to h=\frac{2}{l}
Sustituyendo en 1.
2l+2\left(\frac{2}{l}\right)=6
Simplificamos.
2l+\frac{4}{l}=6
2{l}^{2}+4=6l
2{l}^{2}-6l+4=0
Dividimos a toda la expresión entre 2.
{l}^{2}-3l+2=0
Para calcular el valor numérico del ancho de la ventana, debemos resolver la ecuación.
Comparando con las opciones del problema, escogemos como respuesta correcta a la opción A.
Reactivo 14: Problema con proporciones
Se funden x gramos de plata con 200 g de una aleación que contiene 75% de este metal. Identifique la ecuación que permite calcular los x gramos de plata pura para que la nueva aleación tenga 90% de plata.
- \frac{150+x}{200+x}=0.9
- \frac{200+x}{150+x}=0.9
- \frac{75+x}{200+x}=0.9
- \frac{200+x}{75+x}=90
- \frac{150+x}{200+x}=90
Solución:
Para calcular los gramos de plata pura que debe llevar la nueva aleación y conseguir una concentración del 90%, debemos dividir los gramos de plata pura con los gramos totales de la aleación resultante y ese cociente igualarlo al 90% solicitado.
De esa forma, podríamos luego despejar el valor de los x gramos de plata que se deben agregar para obtener una aleación con el porcentaje indicado.
Los gramos de plata pura en la aleación final se calculan sumando a x la porción de la aleación de mezcla que contiene plata pura, es decir el 75% de los 200 g.
x+200\bullet 0.75=x+150
Por otra parte, los gramos de aleación total se obtienen sumando a x los gramos totales de la aleación de mezcla.
x+200
Finalmente, hacemos el cociente gramos de plata con gramos de aleación y lo igualamos a 0.9:
\frac{x+150}{x+200}=0.9
Comparando con las opciones, escogemos como respuesta correcta a la A.
Reactivo 15: Relaciones con ángulos
En un triángulo rectángulo uno de los ángulos agudos es 10° mayor que el triple del otro. Determinar la medida del mayor entre ellos.
- 75°
- 65°
- 80°
- 70°
- 60°
Solución:
En todo triángulo rectángulo, se cumple que la suma de los ángulos internos es igual a 180°, además el mayor de los ángulos mide 90°. Si denominamos a uno de los ángulos \alpha y al otro \beta la relación anterior se expresa como:
\alpha +\beta +90°=180°
\alpha +\beta =90°
Por otro lado, el problema nos dice que:
…uno de los ángulos agudos es 10° mayor que el triple del otro…
Antes de traducirlo a ecuación, debemos establecer cuál será el ángulo mayos. Diremos que será mayor \alpha . Por tanto, alfa debe ser 10° mayor que el triple de beta.
\alpha =10+3\beta
Como el problema solicita el valor del mayor de ellos, despejamos de la primera ecuación a beta y la expresión resultante se sustituye en la segunda ecuación.
\alpha +\beta =90°\to \beta =90-\alpha
Sustituimos.
\alpha =10+3\left(90-\alpha \right)
Despejamos alfa.
\alpha =10+270-3\alpha
4\alpha =280
\alpha =\frac{280}{4}=70°
El ángulo mayor mide 70°.
Comparando con las opciones, escogemos como correcta a la D.
Reactivo 16: Problemas matemáticos
Una piscina se puede llenar en 7 horas (h) cuando se usan dos grifos, A y B, a la vez. Cuando solo se utiliza uno de estos para llenar la piscina, al grifo B le toma la mitad de tiempo que necesita el grifo A ¿En cuántas horas el grifo A llena la piscina?
- 21 h
- 10.5h
- 14 h
- 24 h
- 12 h
Solución:
Debemos establecer una relación entre los grifos y el tiempo que tardan en llenar la piscina. Por un lado, tenemos que si se emplean ambos grifos a la vez el tiempo de llenado es de 7 horas pero, si se utiliza un solo grifo el tiempo de llenado lógicamente debe ser mayor y debemos establecer una relación inversa.
A menor número de grifos mayor es el tiempo de llenado.
Cuando se utilizan ambos, el tiempo es de 7 horas.
A+B\to 7 h
Cuando solo se utiliza el grifo A.
A\to {t}_{a}
Para calcular el tiempo del grifo A, empleamos una regla de tres inversa.
\frac{A+B}{A}=\frac{{t}_{a}}{7}
Se dividen las relaciones anteriores pero se invierte un lado, en este caso el tiempo. El enunciado nos dice que el grifo B tarda la mitad que el grifo A.
B=\frac{A}{2}
Sustituimos en la primera relación.
\frac{A+\frac{A}{2}}{A}=\frac{{t}_{a}}{7}
Simplificamos y despejamos a {t}_{a} .
{t}_{a}=7\bullet \frac{3}{2}=10.5 h
Comparando el resultado con las opciones del problema, seleccionamos como correcta a la B.
Reactivo 17: Porcentajes y proporciones
Los hermanos Juan, Pedro y Luis compraron una casa por la que pagaron $3 000 000. Pedro aportó el doble que Juan y Luis tanto como Juan y Pedro juntos ¿Qué porcentaje aproximado, del costo de la casa pagó Pedro?
- 30%
- 33%
- 40%
- 35%
- 45%
Solución:
Lo primero que podemos establecer acerca del pago de la casa, es que los tres hermanos han aportado dinero, por tanto:
P+L+J=100\%
Es decir, el aporte conjunto de Pedro, Luis y Juan es el 100% del costo. Ya que se nos pide conocer cuánto porcentaje ha pagado Pedro, debemos dejar a la ecuación anterior expresada sólo en términos de P.
La primera relación que podemos emplear para esto, es que Pedro aportó el doble que Juan.
P=2J
Despejando a Juan tenemos:
J=\frac{P}{2}
Luis aportó tanto como Pedro y Juan juntos.
L=P+J
Sustituyendo J en función de P:
L=P+\frac{P}{2}=\frac{3}{2}P
Ahora, solo queda sustituir ambas relaciones en la primera ecuación.
P+\frac{3}{2}P+\frac{P}{2}=100\%
Simplificamos.
3P=100\%
\therefore P=33.33\%
Que podemos expresar como aproximadamente igual a 33%.
P\cong 33\%
Pedro pagó aproximadamente un 33% de los tres millones de pesos.
Finalmente, escogemos como respuesta correcta a la opción B.
Reactivo 18: Ecuaciones lineales
Una casa puede ser pintada por Diego en 10 días (d), o bien por Emilio en 15 d ¿En cuánto tiempo pintarían la casa Diego y Emilio si trabajasen juntos?
- 12.5 d
- 5 d
- 6 d
- 7.5 d
- 8 d
Solución:
A partir de los datos suministrados, debemos establecer una relación entre el trabajo hecho por día y la duración total.
Ordenamos los datos en una tabla.

Si llamamos al tiempo de duración x podemos combinar el trabajo diario de Emilio y Diego en una misma ecuación ya que, una vez transcurridos los x días, si trabajan juntos habrán pintado la casa por completo.
x\bullet \frac{1}{10}+x\bullet \frac{1}{15}=1
Como cada fracción representa la porción de casa pintada por día de Diego y Emilio respectivamente, si se multiplica por el tiempo total el resultado será la casa pintada. Despejamos a x de la ecuación.
x=\frac{1}{\frac{1}{10}+\frac{1}{15}}=\frac{1}{\frac{1}{6}}=6 días
Si Emilio y Diego combinan esfuerzos, la casa estará lista en 6 días. Concluimos seleccionando como respuesta correcta a la opción C.
Reactivo 19: Sucesiones numéricas
Considerando la sucesión numérica:
0, 3, -6, -3, 6, 9, -18, \dots
¿Cuál de las siguientes sucesiones se rige por la misma regla?
- 0,-3,-1,-4,-2,\dots
- -\mathrm{1,2},-4, 8,-16,\dots
- -5,-2, 4, 7,-14,\dots
- 1,-3,-1,-5,-3,\dots
- 0, 4, 2, 6, 4,\dots
Solución:
Debemos identificar la ley que rige a la sucesión dada y con ella determinar qué inciso cumple con ella.
Analizando, observamos que el segundo término se obtiene de sumar 3 al primero, es decir: 0+3=0 . El tercero de multiplicar por -2 al segundo: \left(3\right)\left(-2\right)=-6 y el cuarto se obtiene sumando nuevamente 3 al anterior, es decir: -6+3=-3 .
Por tanto, la ley de la sucesión es sumar 3, multiplicar por -2, sumar 3, multiplicar por -2,… Debemos ahora identificar qué sucesión de los incisos sigue esta ley.
La del inciso A no puede ser, ya que pasa de 0 a -3, es decir comienza restando 3 y no sumando 3.
La del inciso B parece coincidir pero se diferencia en el cuarto término. Luego de -4 toca sumar 3 y el resultado debería ser -1 pero es 8.
En el inciso C se cumple el patrón por completo:
{a}_{1}=-5
{a}_{2}=-5+3=-2
{a}_{3}=\left(-2\right)\left(-2\right)=4
{a}_{4}=4+3=7
{a}_{5}=\left(7\right)\left(-2\right)=-14
⋮
En el D y E evidentemente no se cumple el patrón, una pasa de 1 a -3 y la otra de 0 a 4. Con todo este análisis, concluimos que la sucesión correcta es la C.
-5,-2, 4, 7,-14,\dots
Reactivo 20: Sucesiones con reglas diferentes
¿Cuál de las siguientes sucesiones numéricas tiene una regla diferente?
- -5,-1,-\mathrm{3,1},-1,\dots
- 1,-3,-1,-5,-3,\dots
- 2, 6, 4, 8, 6,\dots
- -1, 3, 1, 5, 3,\dots
- 0, 4, 2, 6, 4,\dots
Solución:
Debemos determinar qué regla sigue cada sucesión para así indicar cuál de ellas sigue una diferente.
Sucesión A.
El segundo término se obtiene al sumar 4 al primero -5+4=-1 , el tercero de sumar -2 al segundo -1-2=-3 , el cuarto de sumar 4 al tercero -3+4=1 y el quinto de sumar -2 al cuarto 1-2=-1 .
Sucesión B.
Evidentemente no sigue la misma regla que la A. En este caso, se restan 4 luego se suman 2,…
Sucesión C.
En este caso, la regla es la misma que en la A. Primero se suman 4, luego se restan 2,… Podemos suponer que esta será la regla del resto de sucesiones y que la B es la que tiene una regla diferente.
Sucesiones D y E.
En efecto, la regla es +4, -2, +4, -2,… Concluimos entonces que la sucesión B es la que tiene una regla diferente.
Reactivo 21: Perímetro de un triángulo
Expresar el perímetro P de un triángulo equilátero en términos de su altura h .
P=\frac{ }{ }
- 2\sqrt{3}h
- 4h
- \frac{6}{\sqrt{5}}h
- \frac{\sqrt{3}}{4}h
- \frac{3\sqrt{3}}{2}h
Solución:
Un triángulo equilátero es aquel cuyos tres lados miden igual y sus tres ángulos internos son también iguales y de 60°.
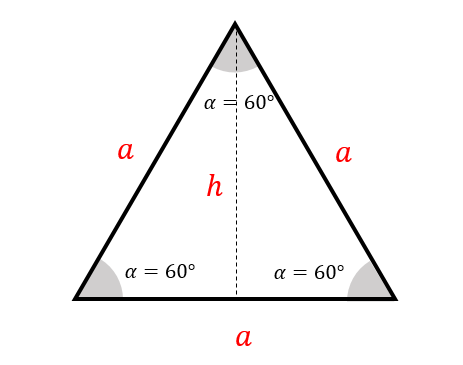
De esta forma, el perímetro del triángulo se calcula como:
P=3a
Ahora, debemos expresar al lado a en función de la altura del triángulo, para ello nos valdremos de una de los triángulos rectángulos que se forman.
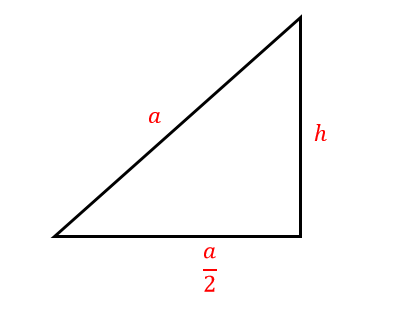
Aplicando el teorema de Pitágoras nos queda que:
{a}^{2}=\frac{{a}^{2}}{4}+{h}^{2}
{h}^{2}={a}^{2}-\frac{{a}^{2}}{4}=\frac{3}{4}{a}^{2}
h=\frac{\sqrt{3}}{2}a\to a=\frac{2\sqrt{3}}{3}h
Sustituimos en la ecuación del perímetro.
P=3\left(\frac{2\sqrt{3}}{3}h\right)
P=2\sqrt{3}h
Comparando nuestro resultado con las opciones, la respuesta correcta es la A.
Reactivo 22: Problemas matemáticos
Un comerciante mezcla café veracruzano de $130 el kg con café chiapaneco de $115 y obtiene 100 kg que vende a $120.25 el kg ¿Cuántos kilogramos uso de café veracruzano?
- 30.5 kg
- 40.5 kg
- 65 kg
- 35 kg
- 48 kg
Solución:
En este caso, debemos armar un SE con los datos que nos proporciona el enunciado. Sabemos que los 100 kg de café resultantes se obtienen al mezclar un determinado peso de café veracruzano {P}_{cv} con otro de café chiapaneco {P}_{cc} .
{P}_{cv}+{P}_{cc}=100
Además, los precios están dados por kilogramo de café, es decir \frac{\$}{kg} para obtener el precio absoluto de cada porción, podemos multiplicar el peso por su respectiva relación precio/kilogramo.
130{P}_{cv}+115{P}_{cc}=\left(100\right)\left(120.25\right)
130{P}_{cv}+115{P}_{cc}=12025
De esta forma, tenemos un sistema de dos ecuaciones y dos incógnitas.
\left\{\begin{array}{c} P_{c v}+P_{c c}=100 \\ 130 P_{c v}+115 P_{c c}=12025 \end{array}\right.
Se puede emplear cualquier método de resolución conocido. Ya que solo nos interesa el peso de la porción de café veracruzano, despejamos de la primera ecuación a {P}_{cc} para sustituir en la segunda ecuación.
{P}_{cc}=100-{P}_{cv}
130{P}_{cv}+115\left(100-{P}_{cv}\right)=12025
Simplificamos.
130{P}_{cv}+11500-115{P}_{cv}=12025
15{P}_{cv}=525
{P}_{cv}=\frac{525}{15}=35 kg
El comerciante utilizó 35 kg de café veracruzano en la mezcla. Finalmente, escogemos como respuesta correcta a la opción D.


