¡Hola de nuevo aspirante! En este tutorial estaremos resolviendo paso a paso los reactivos del 24 al 32 de la segunda parte de la guía de matemáticas para el examen de admisión a la UAM, en la división de Ciencias Básicas e Ingeniería y Ciencias Naturales e Ingeniería.

Guía UAM Matemáticas Parte 2 resuelta
Continuamos con la solución paso a paso de los reactivos de matemáticas para el examen de ingreso a la UAM en las áreas CBI y CNI.
Recuerda, si has llegado hasta acá, pero aun no los resuelves por tu cuenta ¡hazlo! Tu nota en el examen dependerá de lo lo bien que domines cada uno de los temas.
Reactivo 23: Sistema de ecuaciones lineales
José y Juan recibirán un salario mensual de $10 000 cada uno. Después de cierto tiempo Juan obtuvo un mejor empleo con un sueldo mensual de $15 000. Si entre ambos ganaron $530 000 en un periodo de 2 años ¿Cuál es la ecuación que permite determinar el número x de meses estuvo Juan en el primer trabajo?
- 240+10x+360+15x=530
- 240+240-10x+15x=530
- 240+10x+360-x=530
- 240+240-x+15x=530
- 240+10x+360-15x=530
Solución:
El problema nos proporciona diferentes relaciones entre los sueldos de Juan y José, con el tiempo transcurrido. Primero, sabemos que juntos ganaron un total de $530 000 en 24 meses (2 años) y que José nunca cambió de trabajo, por tanto durante ese tiempo su ingreso total fue:
\left(24\right)\left(\$10 000\right)=\$240 000
Como consecuencia, el ingreso de Juan fue de:
\$530 000-\$240 000=\$290 000
De esos $290 000, durante x meses gano $10 000 y durante otros y meses ganó $15 000. Esto se puede escribir como:
10000x+15000y=290000
Debemos deshacernos de la variable y , esto lo haremos gracias a que x y y suman 24 meses (2 años).
x+y=24
Despejamos a y y la sustituimos en la primera ecuación.
y=24-x
10000x+15000\left(24-x\right)=290000
10000x+360000-15000x=290000
Dividimos la ecuación entre 1000.
10x+360-15x=290
Aunque esta es la respuesta y puede incluso simplificarse más, los incisos están igualados a 530, para dejar la respuesta expresada de esta forma, debemos sumar en ambos miembros 240.
240+10x+360-15x=530
Comparando con las opciones, escogemos a la E como la respuesta correcta. Como dato extra, si se resuelve la ecuación final, sabremos que Juan estuvo 14 meses ganando $10 000 al mes.
Reactivo 24: Sistema de ecuaciones lineales
Al abrir su alcancía Sara encontró que tenía $4 800 en billetes de $50, $100 y $200. También observó que el número de billetes de $100 era el triple de los billetes de $200 y que los de $50 eran el doble de los de $100 ¿Cuántos billetes de $100 habían en la alcancía?
- 21
- 18
- 15
- 12
- 6
Solución:
En este caso, debemos extraer ecuaciones a partir del enunciado que relacionen el número de billetes para armar un sistema de ecuaciones y así determinar la cantidad de billetes de $100 en la alcancía de Sara.
Llamaremos x al número de billetes de $50, y al de $100 y z a la cantidad de billetes de $200. Los $4800 son iguales a la suma de los billetes de cada denominación, es decir:
4800=50x+100y+200z
Por otra parte, sabemos que el número de billetes de $100 era el triple de los billetes de $200: y=3z y que los de $50 eran el doble de los de $100: x=2y . De esta forma, el sistema de ecuaciones final es:
\left\{\begin{array}{c}4800=50x+100y+200z\\ y=3z x=2y\end{array}\right.
Como solo nos interesa la cantidad de billetes de $100, es decir y sustituimos en la primera ecuación a x y z en función de y .
x=2y
z=\frac{y}{3}
Sustituyendo.
4800=50\left(2y\right)+100y+\frac{200y}{3}
Despejamos a x .
4800=100y+100y+\frac{200}{3}y
y\left(200+\frac{200}{3}\right)=4800
\frac{800}{3}y=4800
y=18
Comparando nuestro resultado con las opciones del problema, seleccionamos como correcta a la B.
Reactivo 25: Trigonometría
En una avenida se encuentran dos edificios, uno frente al otro, cuyas bases están a 40 m de distancia. La altura de uno es de 45 m y la del otro es de 35 m. Si una persona se coloca en la avenida entre los dos edificios ¿a qué distancia del edificio más alto debe situarse para que su distancia a la azotea de cada edificio sea la misma?
- 17.5 m
- 12.5 m
- 15 m
- 20 m
- 10 m
Solución:
Para facilitar el análisis del problema, hagamos un bosquejo de la situación planteada.
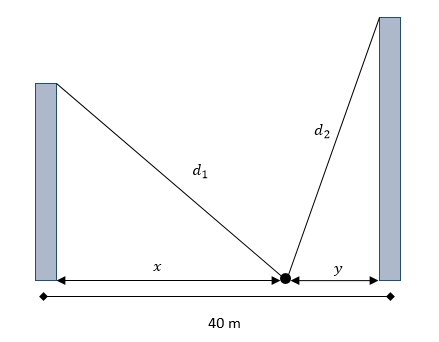
El punto negro representa a la persona situada entre los dos edificios, {d}_{1} y {d}_{2} la distancia medida desde el punto hasta la azotea y x y y las distancias entre las bases de los edificios y la persona. En este caso solo nos interesa y , porque es la distancia a la base del edificio más alto.
Por trigonometría, sabemos que:
{d}_{1}^{2}={35}^{2}+{x}^{2}
{d}_{2}^{2}={45}^{2}+{y}^{2}
Además, la suma de x con y es siempre 40 m.
x+y=40
Igualamos las distancias a las azoteas.
{d}_{1}^{2}={d}_{2}^{2}\to {35}^{2}+{x}^{2}={45}^{2}+{y}^{2}
Acomodamos la expresión.
{x}^{2}-{y}^{2}={45}^{2}-{35}^{2}
Despejamos x de la segunda ecuación.
x=40-y
Sustituimos y simplificamos.
{\left(40-y\right)}^{2}-{y}^{2}={45}^{2}-{35}^{2}
{40}^{2}-80y+{y}^{2}-{y}^{2}={45}^{2}-{35}^{2}
80y={40}^{2}+{35}^{3}-{45}^{2}
y=\frac{{40}^{2}+{35}^{3}-{45}^{2}}{80}=10
La persona debe situarse a 10 metros del edificio más alto para mantener la misma distancia respecto a las azoteas.
Comparando con las opciones, seleccionamos como correcta a la E.
Reactivo 26: Razonamiento matemático
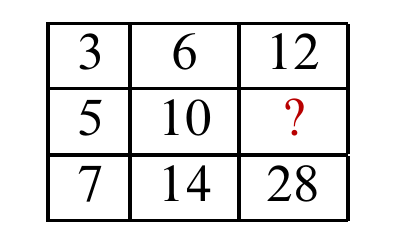
En el siguiente arreglo rectangular ¿Cuál es el número que falta?
- 40
- 15
- 20
- 30
- 25
Solución:
Para encontrar el número faltante, debemos identificar la ley que hace cambiar a los números. El patrón puede hacer que los números aumenten o disminuyan de forma vertical, horizontal o en diagonal.
En este caso, cada fila comienza con un número y aumenta el doble a medida que nos desplazamos en las filas de izquierda a derecha. Por tanto, el número restante es:
10\times 2=20
Comparando con las opciones, escogemos como correcta a la C.
Reactivo 27: Razonamiento matemático
En el siguiente arreglo rectangular ¿Cuál es la letra que falta?
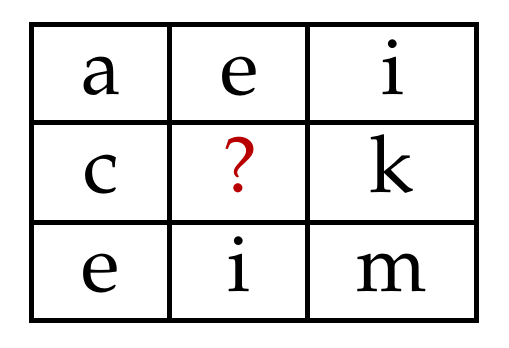
- F
- G
- H
- I
- E
Solución:
Debemos identificar la ley que hace cambiar a las letras. Si escribimos el abecedario hasta la m, nos daremos cuenta que las letras en cada fila distan 4 espacios entre ellas.
a, b, c, d, e, f, g, h, i, j, k, l, m,\dots
En la primera, hay que recorrer 4 espacios desde la a hasta la e y luego 4 más desde la e hasta la i.
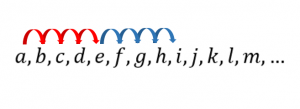
Lo mismo sucede en la tercera fila, hay 4 espacios de la e a la i y 4 más hasta la m.

En base a nuestro análisis, la letra que falta es la g ya que 4 espacios después de la c se encuentra la g. Concluimos escogiendo como respuesta correcta a la opción B.
Reactivo 28: Proporciones
Para preparar algunos postres, Sara necesitará azúcar; para el pastel requerirá 3/8 de taza y para las galletas usará 3/4 de taza. Si solo hay 15/16 de taza de azúcar ¿Cuál de las siguientes opciones es correcta?
- Tiene apenas suficiente azúcar
- Necesita 9/4 de taza extra
- Necesita 3/16 de taza
- Le sobran 3/8 de taza
- Le sobran 3/16 de taza
Solución:
El total de azúcar que Sara necesitará es:
\frac{3}{8}+\frac{3}{4}=\frac{9}{8} de taza
Para saber si le sobra o falta, debemos restar los 15/16 que tiene a los 9/8 que necesita. Si el resultado es negativo le falta esa cantidad y si es positivo le sobra.
\frac{15}{16}-\frac{9}{8}=-\frac{3}{16}
A Sara le hacen falta 3/16 de taza para preparar ambos postres. Comparando con las opciones, la respuesta correcta es la C.
Reactivo 29: Comparación de fracciones
Dadas las fracciones \frac{2}{13},\frac{1}{4},\frac{5}{3},\frac{9}{8},\frac{8}{5} , la de mayor valor es _______
- \frac{5}{3}
- \frac{2}{13}
- \frac{1}{4}
- \frac{9}{8}
- \frac{8}{5}
Solución:
Para comparar un conjunto de fracciones con diferente numerador y denominador, debemos encontrar el mínimo común múltiplo de todos los denominadores, y luego multiplicar y dividir cada fracción por un número tal que el denominador resultante sea el mcm antes determinado.
- Calculamos el mcm.
mcm\left(\mathrm{13,4},\mathrm{3,8},5\right)
Descomponemos en factores cada número.
13=13\times 1
4={2}^{2}
3=3\times 1
8={2}^{3}
5=5\times 1
Hacemos el producto de los factores con su mayor exponente.
mcm\left(\mathrm{13,4},\mathrm{3,8},5\right)=13\times {2}^{3}\times 3\times 5=1560
- Multiplicamos y dividimos cada fracción por un número que haga que el denominador sea igual al mcm
Fracción 1.
\frac{1560}{13}=120
\frac{2\bullet 120}{13\bullet 120}=\frac{240}{1560}
Fracción 2.
\frac{1560}{4}=390
\frac{390}{4\bullet 390}=\frac{390}{1560}
Fracción 3.
\frac{1560}{3}=520
\frac{5\bullet 520}{3\bullet 520}=\frac{2600}{1560}
Fracción 4.
\frac{1560}{8}=195
\frac{9\bullet 195}{8\bullet 195}=\frac{1755}{1560}
Fracción 5.
\frac{1560}{5}=312
\frac{8\bullet 312}{5\bullet 312}=\frac{2496}{1560}
- Comparamos los numeradores de las fracciones
Ya que los denominadores son iguales, la fracción mayor será aquella que tenga el mayor numerador.
\frac{240}{1560}, \frac{390}{1560}, \frac{2600}{1560},\frac{1755}{1560},\frac{2496}{1560}
En este caso, es la fracción con numerador igual a 2600 la de mayor valor. Dicha fracción es equivalente a:
\frac{2600}{1560}=\frac{5}{3}
Comparando con las opciones, escogemos como correcta al inciso A.
Dadas las fracciones \frac{2}{13},\frac{1}{4},\frac{5}{3},\frac{9}{8},\frac{8}{5} , la de mayor valor es \frac{5}{3}
Reactivo 30: Operaciones con fracciones
El resultado de \frac{\frac{3}{2}-\frac{2}{3}}{\frac{3}{2}+\frac{1}{4}} es ____________.
- \frac{35}{24}
- -\frac{8}{3}
- \frac{10}{21}
- -\frac{\frac{3}{2}}{\frac{1}{4}}
- -\frac{10}{21}
Solución:
Para encontrar el resultado, debemos realizar cada una de las operaciones dentro de la fracción. Primero, resolvemos la resta de fracciones en el numerador, luego la suma en el denominador y por último aplicar la regla del sándwich.
Resta en el numerador, aplicamos el producto cruzado.
\frac{\frac{3}{2}-\frac{2}{3}}{\frac{3}{2}+\frac{1}{4}}=\frac{\frac{9-4}{6}}{\frac{3}{2}+\frac{1}{4}}
\frac{\frac{5}{6}}{\frac{3}{2}+\frac{1}{4}}
Suma en el denominador, de nuevo el producto cruzado.
\frac{\frac{5}{6}}{\frac{3}{2}+\frac{1}{4}}=\frac{\frac{5}{6}}{\frac{12+2}{8}}
\frac{\frac{5}{6}}{\frac{14}{8}}
Regla del sándwich.
\frac{\frac{5}{6}}{\frac{14}{8}}=\frac{5\bullet 8}{6\bullet 14}
\frac{40}{84}
Simplificamos la fracción.
\frac{40}{84}=\frac{20}{42}=\frac{10}{21}
Concluimos que:
\frac{\frac{3}{2}-\frac{2}{3}}{\frac{3}{2}+\frac{1}{4}}=\frac{10}{21}
Concluimos el reactivo escogiendo como respuesta correcta a la opción C.
Reactivo 31: Regla de tres
Un auto puede recorrer 180 km con 12 L de gasolina ¿Qué distancia puede recorrer con 20 L?
- 350 km
- 280 km
- 325 km
- 300 km
- 200 km
Solución:
Antes de realizar la regla de tres, debemos identificar si la relación entre los kilómetros recorridos y la gasolina en el tanque es lineal o inversa. Por simple lógica, mientras mayor gasolina tenga el auto más kilómetros podrá recorrer, por ende es una relación lineal.
Regla de tres lineal.
12 L\to 180 km
20 L\to x
x=\frac{20 L\bullet 180 km}{12 L}=300 km
El conductor podrá recorrer 300 km si tiene en el tanque 20 litros.
Seleccionamos como respuesta correcta a la opción D.
Reactivo 32: Porcentajes
El 0.56% del número N es 196 ¿Cuál es el número N ?
- 100 000
- 35 000
- 128 000
- 19 600
- 40 000
Solución:
Este problema podemos resolverlo fácilmente con la definición de porcentaje.
\%=\frac{{N}_{\%}}{N}*100\%
Donde N es la cantidad total, {N}_{\%} es una cantidad que representa un porcentaje de N y \% es el porcentaje de {N}_{\%} respecto de N . El enunciado solicita que calculemos cuánto debe ser N para que el \%=0.56\% sea {N}_{\%}=196 .
Debemos despejar a N de la definición de porcentaje para encontrar su valor.
\%=\frac{{N}_{\%}}{N}*100\%\to N=\frac{{N}_{\%}}{\%}*100\%
Sustituimos.
N=\frac{196}{0.56\%}*100\%=35 000
N debe valer 35 000 para que su 0.56% sea igual a 196.
Concluimos el ejercicio escogiendo como respuesta correcta a la opción B.

