¿Tienes problemas con la guía de Física del IPN? ¡No te preocupes! En este tutorial vamos a resolver paso a paso los 50 reactivos de física de la guía IPN 2023 rama de ingeniería y ciencias físico matemáticas.

Por motivos de aprendizaje hemos dividido la guía en 5 partes para que tengas en cuenta las pasusas activas entre cada bloque de estudio.
Te dejo un resumen puntual de la convocatoria IPN.
- Carreras ofertadas en IPN: 70+.
- Porcentaje de Aceptación: 20%.
- Preguntas en el examen de Admisión: 140 preguntas.
- Nuevos temas: historia e inglés (reading comprehension).
- Tipo: selección múltiple.
Estructura del Examen IPN
La estructura del examen de ingreso al Instituto Politécnico Nacional este 2023 ha sido modificada. Ahora, el total de reactivos por asignatura cambia según el área de conocimientos. Las carreras que ofrece el IPN se dividen en 3 áreas del conocimiento:
- Ingeniería y Ciencias Físico Matemáticas IyCFM
- Ciencias Sociales y Administrativas CSA
- Ciencias Médico Biológicas CMB
La siguiente tabla muestra la estructura de reactivos por materia para cada área.
| Materia | IyCFM | CMB | CSyA |
|---|---|---|---|
| Matemáticas | 37 | 33 | 35 |
| Competencia escrita | 20 | 20 | 25 |
| Competencia lectora | 20 | 20 | 20 |
| Reading comprehension | 10 | 10 | 10 |
| Historia | 10 | 10 | 20 |
| Biología | 9 | 17 | 10 |
| Química | 17 | 17 | 10 |
| Física | 17 | 13 | 10 |
¿Qué tan difícil es el examen al IPN?
Una pregunta común entre los aspirantes al IPN es: ¿qué tan difícil es entrar al IPN? La respuesta depende de un único factor: las ganas que inviertes en tu preparación antes del examen.
Para la convocatoria se incluyen 2 nuevas asignaturas, lo que aumenta el total de reactivos a 140. En la guía de física para el área de Ingeniería y Ciencias Físico Matemáticas, se incluyen reactivos que cubren el temario de física clásica del bachillerato.
Temario de física del área IyCFM IPN 2023
Estos son los temas de física que deberás estudiar antes de presentar el examen:
| Tema | Rama |
|---|---|
| Sistemas de unidades y mediciones | IyCFM, CMB |
| Álgebra vectorial | IyCFM, CMB |
| Cinemática | IyCFM, CSyA |
| Estática | IyCFM, CMB, CSyA |
| Leyes de newton | IyCFM |
| Propiedades de la materia | IyCFM, CSyA |
| Termodinámica | IyCFM, CMB |
| Electroestática | IyCFM |
| Electrodinámica | IyCFM |
| Celdas electroquímicas | IyCFM |
| Electromagnetismo | IyCFM, CMB |
| Ondas | IyCFM, CSyA |
¿Cómo resolver la guía del IPN 2023?
La dinámica es sencilla, los ejercicios que vienen en la guía son un adelanto de lo que puede salir en el examen. Por ello, lo primero que debes hacer es familiarizarte muy bien con los puntos de física que específica el temario, consultar la bibliografía recomendada en la guía e ir paso a paso resolviendo los ejercicios con nuestra ayuda hasta que los domines por completo.
No comiences a resolver sin tener una idea de los temas que saldrán. Estudiar de esta forma te hará perder tiempo e irás a ciegas sin una metodología establecida.
Los siguientes consejos te ayudarán a mejorar tu desempeño para obtener los aciertos que necesitas para ser admitido.
- Resuelve cada parte por tu cuenta antes de checar las respuestas. Utiliza este material a modo de consulta.
- Establece un tiempo no mayor a 15 minutos por cada 10 reactivos.
- Analiza el procedimiento al resolver los ejercicios y piensa en posibles alternativas que mejoren tu tiempo.
- Si un ejercicio parece complejo, ve al siguiente y resuélvelo de último. Lo mejor es mantener la concentración y no entrar en pánico.
- Te advierto que la guía del IPN 2023 tiene algunos errores, aquí te señalamos cuáles son.
- Física no se trata de aplicar fórmulas. Debes conocer los fundamentos, analizar los enunciados y seleccionar las leyes físicas correctas para resolver el problema.
Reactivo 1
Para un objeto en movimiento, la velocidad v en \mathrm{m}/\mathrm{s} de un automóvil viene dada por v=a{t}^{2}+b{t}^{3} , donde el tiempo (t) está en segundos. ¿Qué valor corresponde a las unidades a y b, respectivamente?
- m\cdot {s}^{2},m\cdot {s}^{4}
- \frac{{s}^{3}}{m},\frac{{s}^{4}}{m}
- \frac{m}{{s}^{2}},\frac{m}{{s}^{3}}
- \frac{\mathrm{m}}{{\mathrm{s}}^{3}},\frac{\mathrm{m}}{{\mathrm{s}}^{4}}
Solución:
La función que se muestra en el enunciado, es la de velocidad en función del tiempo. Es decir, debemos sustituir un valor de tiempo en segundos, para obtener un resultado en m/s .
Debido a que la función posee dos términos, las unidades de ambos deben ser m/s para que las unidades sean homogéneas al momento de sumar. Para el término a{t}^{2} , el tiempo queda en {s}^{2} por lo tanto, para que el resultado sea \frac{m}{s} , las unidades del coeficiente a deben ser: \frac{m}{{s}^{3}} .
Comprobación de unidades del término a{t}^{2} .
a{t}^{2}=\left[\frac{m}{{s}^{3}}\right]\cdot \left[{s}^{2}\right]=\left[\frac{m}{s}\right]
Debido a que el único inciso que tiene como primera opción m/{s}^{3} es el d), seleccionamos a dicho inciso como la respuesta correcta del ejercicio.
Reactivo 2
Calcular la fuerza de tracción sobre el auto, si a él se ata un extremo de cable y el otro extremo se ata a un árbol, como se muestra en la figura, y se ejerce una fuerza de F = 100 N en el centro del cable.
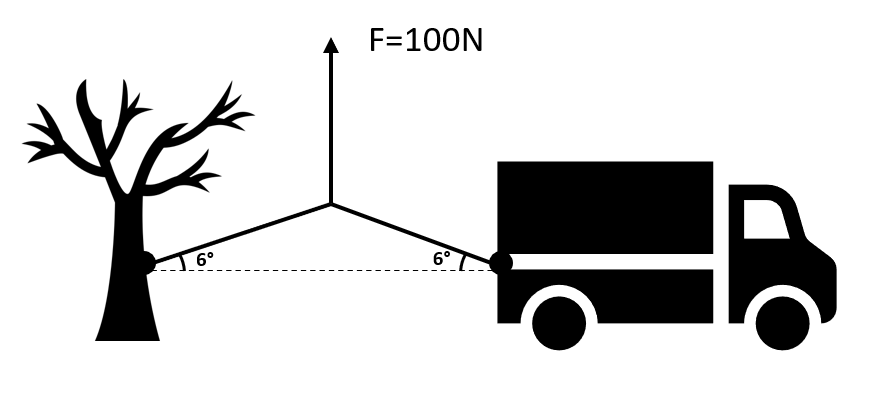
- 1000.16 N
- 478.4N
- 600N
- 400N
Solución:
Para resolver este problema, debemos descomponer las fuerzas aplicando diagrama de cuerpo libre en el punto central de la cuerda. En este caso, la fuerza de tracción es la que experimenta el auto al ser alado.
Debido a que nuestro sistema se encuentra en reposo, debemos aplicar la primera ley de Newton en la descomposición de fuerzas. En el diagrama de cuerpo libre en el centro de la cuerda, actúan tres fuerzas: F , la tensión que ejerce el árbol {T}_{1} y la tensión que ejerce el carro {T}_{2} .
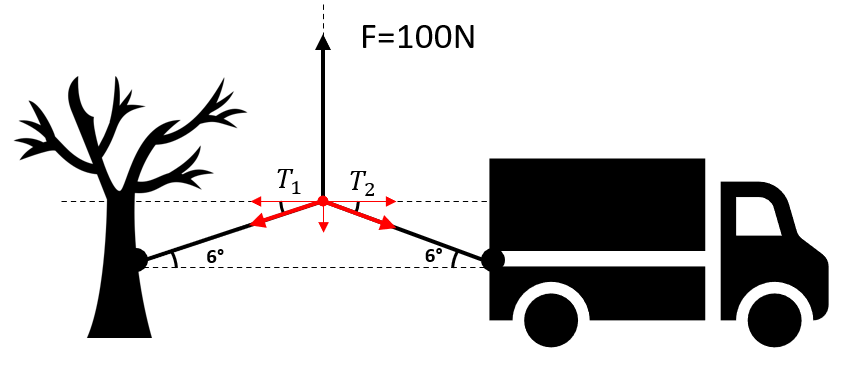
El ángulo que forman los vectores de tensión respecto a la horizontal es el mismo de 6°. De esta forma, las componentes en x y y de las tensiones quedarían como:
Descomposición de la tensión 1.
{T}_{1x}=-{T}_{1}\mathrm{cos}6°
{T}_{1y}=-{T}_{1}\mathrm{sin}6°
Descomposición de la tensión 2.
{T}_{2x}={T}_{2}\mathrm{cos}6°
{T}_{2y}=-{T}_{2}\mathrm{sin}6°
Tengamos en cuenta que {T}_{1} y {T}_{2} son los módulos de los vectores de tensión. Aplicando la primera ley de Newton.
{F}_{x}: {T}_{2}\mathrm{cos}6°-{T}_{1}\mathrm{cos}6°=0
{F}_{y}:F-{T}_{2}\mathrm{sin}6°-{T}_{1}\mathrm{sin}6°=0
A partir de la primera ecuación, obtenemos que los módulos de las tensiones son iguales.
{T}_{2}\mathrm{cos}6°-{T}_{1}\mathrm{cos}6°=0\to {T}_{2}\mathrm{cos}6°={T}_{1}\mathrm{cos}6°
\therefore {T}_{1}={T}_{2}=T
Sustituimos esto en la segunda ecuación.
F-T\mathrm{sin}6°-T\mathrm{sin}6°=0\to F-2T\mathrm{sin}6°=0
F=2T\mathrm{sin}6°\to T=\frac{F}{2\mathrm{sin}6°}
Sustituimos los valores de la fuerza F y calculamos el seno de 6°.
T=\frac{100}{2\mathrm{sin}6°}=478.34 \mathrm{N}
La fuerza de tracción que experimenta el carro es de 478.34 \mathrm{N} .
La respuesta correcta es el inciso b).
Reactivo 3
Calcular el desplazamiento de un automóvil que parte del reposo y se mueve con una aceleración constante de 4\mathrm{m}/{\mathrm{s}}^{2} durante 4s y los próximos 10s avanza con movimiento uniforme.
- 395 m
- 293 m
- 192 m
- 170 m
Solución:
Examinando el enunciado, identificamos dos movimientos: primero hay un MRUA y luego un MRU. Podemos simplificar la información suministrada por el enunciado a partir del siguiente gráfico:
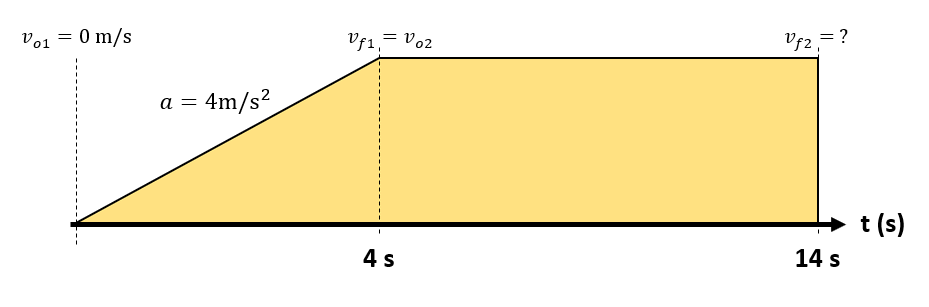
Para el primer desplazamiento empleamos la siguiente ecuación del MRUA:
{x}_{f1}={x}_{o}+{v}_{o}t+\frac{a{t}^{2}}{2}
Tenemos que: {x}_{o}=0 \mathrm{m} , {v}_{o}=0 \mathrm{m}/\mathrm{s} , a=4 \mathrm{m}/{\mathrm{s}}^{2} , t=4 \mathrm{s} .
{x}_{f1}=0+\left(0\right)\left(4\right)+\frac{\left(4\right){\left(4\right)}^{2}}{2}=32 \mathrm{m}
Ahora calculamos la velocidad final del movimiento 1, porque esta será la velocidad inicial para el movimiento 2.
{v}_{f1}={v}_{o1}+at=0+\left(4\right)\left(4\right)=16 \mathrm{m}/\mathrm{s}
Calculamos el desplazamiento para el segundo movimiento.
{x}_{f2}={x}_{o2}+{v}_{2}\left({t}_{2}-{t}_{1}\right)
Sustituimos: {x}_{o2}=32 \mathrm{m} , {v}_{2}=16 \mathrm{m}/\mathrm{s} , {t}_{2}=14 \mathrm{s} , {t}_{1}=4 \mathrm{s} .
{x}_{f2}=32+\left(16\right)\left(14-4\right)=192 \mathrm{m}
El automóvil recorre 192 metros durante todo el desplazamiento.
La respuesta correcta es el inciso c).
Reactivo 4
Determinar el tiempo total de un viaje en automóvil si este recorre una distancia de 170 km y desarrolla, en los primeros 140 km, una velocidad media de 70 km/h, en tanto que en los últimos 30 km presenta una velocidad media de 50 km/h.
- 5h
- 6h
- 0h
- 5h
Solución:
El tiempo total del viaje es igual a la suma de los tiempos en los dos intervalos.
t={t}_{1}+{t}_{2}
Para realizar los cálculos, nos apoyamos en la ecuación de velocidad media.
{v}_{m}=\frac{{x}_{f}-{x}_{i}}{\mathrm{\Delta }t}
El primer intervalo tiene una velocidad media de 70 km/h, inicia en 0 km y termina en 140 km.
70=\frac{140-0}{\mathrm{\Delta }{t}_{1}}\to \mathrm{\Delta }{t}_{1}=\frac{140}{70}=2 \mathrm{h}
Para el segundo intervalo: 50 km/h, inicia en 140 km y termina en 170 km.
50=\frac{170-140}{\mathrm{\Delta }{t}_{2}}\to \mathrm{\Delta }{t}_{2}=\frac{30}{50}=0.6 \mathrm{h}
Finalmente:
t=2+0.6=2.6 \mathrm{h}
El automóvil terminó el recorrido en 2.6 horas.
La respuesta correcta es el inciso b).
Reactivo 5
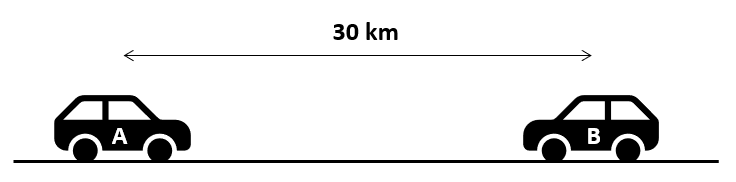
Deducir las velocidades de dos móviles A y B que están separados por una distancia de 30 km. Si se mueven en la misma dirección y sentido se encuentran a 10 km de B, pero si se mueven en sentidos opuestos, tardaran 40 minutos en encontrarse.
- {V}_{A}=\frac{11\mathrm{m}}{\mathrm{s}},{V}_{B}=\frac{2.7\mathrm{m}}{\mathrm{s}}
- {V}_{A}=\frac{10\mathrm{m}}{\mathrm{s}},{V}_{B}=\frac{2.5\mathrm{m}}{\mathrm{s}}
- {V}_{A}=\frac{11\mathrm{m}}{\mathrm{s}},{V}_{B}=\frac{2.6\mathrm{m}}{\mathrm{s}}
- {V}_{A}=\frac{10\mathrm{m}}{\mathrm{s}},{V}_{B}=\frac{2.7\mathrm{m}}{\mathrm{s}}
Solución:
Inicialmente los coches se encuentran separados por una distancia de 30 km y nos plantea dos posibilidades para que estos se muevan.
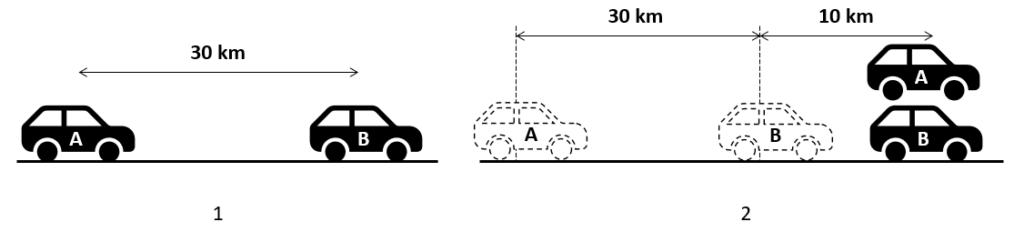
Posibilidad 1: que se mueven en la misma dirección.
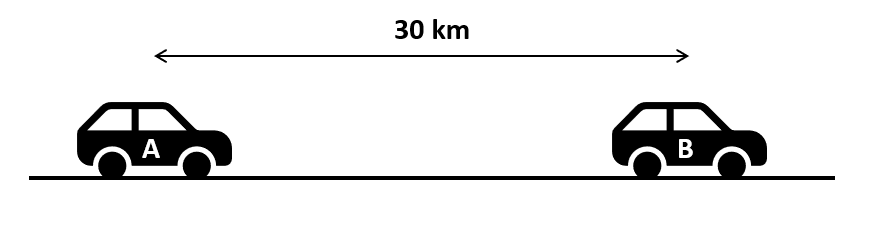
Posibilidad 2: que se muevan en sentidos opuestos.
En ambos casos, asumimos que el movimiento es rectilíneo uniforme. Debemos tomar los datos de ambos movimientos y formar un sistema de ecuaciones. Vamos con los datos del primer caso.
Las ecuaciones de movimiento rectilíneo uniforme para ambos carros son:
{x}_{fA}={x}_{oA}+t{V}_{A}
{x}_{fB}={x}_{oB}+t{V}_{B}
La posición inicial para el carro A es 0 y la final es 40 km, mientras que la posición inicial de B es 30 km y la final es 40 km. Despejamos el tiempo e igualamos las expresiones.
40=t{V}_{A}\to t=\frac{40}{{V}_{A}}
10=t{V}_{B}\to t=\frac{10}{{V}_{B}}
Igualando.
\frac{40}{{V}_{A}}=\frac{10}{{V}_{B}}\to 10{V}_{A}=40{V}_{B}\to 10{V}_{A}-40{V}_{B}=0
{V}_{A}-4{V}_{B}=0
Para el segundo movimiento, debemos transformar el tiempo de encuentro a horas.
40\mathrm{ }\mathrm{m}\mathrm{i}\mathrm{n}\cdot \frac{1 \mathrm{h}}{60 \mathrm{m}\mathrm{i}\mathrm{n}}=0.66 \mathrm{h}
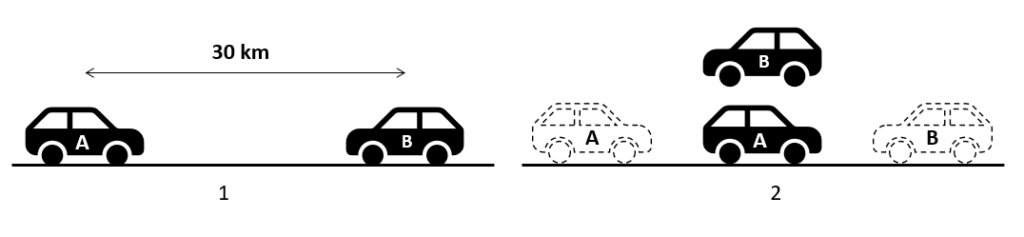
La posición inicial de A es cero, mientras que la posición inicial de B es 30 km. En este caso, la velocidad de A es positiva y la velocidad de B es negativa. La velocidad final es igual para ambos carros.
{x}_{f}={x}_{oA}+t{V}_{A}
{x}_{f}={x}_{oB}-t{V}_{B}
Igualamos y sustituimos.
{x}_{oA}+t{V}_{A}={x}_{oB}-t{V}_{B}
0.66\cdot {V}_{A}=30-0.66\cdot {V}_{B}
{V}_{A}+{V}_{B}=\frac{30}{0.66}\to {V}_{A}+{V}_{B}=45
El sistema de ecuaciones es:
\left\{\begin{array}{c}{V}_{A}+{V}_{B}=45\\ {V}_{A}-4{V}_{B}=0\end{array}\right.
Resolviendo el sistema de ecuaciones (saltaremos este paso, pero puedes emplear cualquier método que conozcas), los valores de {V}_{A} y {V}_{B} son:
{V}_{A}=36\frac{\mathrm{k}\mathrm{m}}{\mathrm{h}}, {V}_{B}=9\frac{\mathrm{k}\mathrm{m}}{\mathrm{h}}
Transformamos a metros por segundo para comparar con los enunciados.
{V}_{A}=36\frac{\mathrm{k}\mathrm{m}}{\mathrm{h}}\cdot \frac{1 \mathrm{h}}{3600 \mathrm{s}}\cdot \frac{1000\mathrm{ }\mathrm{m}}{1 \mathrm{k}\mathrm{m}}=10\frac{\mathrm{m}}{\mathrm{s}}
{V}_{B}=9\frac{\mathrm{k}\mathrm{m}}{\mathrm{h}}\cdot \frac{1 \mathrm{h}}{3600 \mathrm{s}}\cdot \frac{1000\mathrm{ }\mathrm{m}}{1 \mathrm{k}\mathrm{m}}=2.5\frac{\mathrm{m}}{\mathrm{s}}
Concluimos el ejercicio seleccionando como respuesta correcta al inciso b).
Reactivo 6
Determinar la altura que alcanza una bala, si esta se dispara hacia arriba a una velocidad de 50\mathrm{m}/\mathrm{s} . Considerar \mathrm{g}=9.81\mathrm{m}/{\mathrm{s}}^{2} ?
- 9.8 m
- 45.0 m
- 127.42m
- 200.0 m
Solución:
Para resolver el problema, empleamos las ecuaciones de lanzamiento vertical de cuerpos.
\begin{array}{c}{y}_{f}={y}_{o}+{v}_{o}t-\frac{g{t}^{2}}{2}\\ \begin{array}{c}{v}_{f}={v}_{o}-gt\\ {v}_{f}^{2}={v}_{o}^{2}-2g\left({y}_{f}-{y}_{o}\right)\end{array}\end{array}
En el lanzamiento vertical, cuando un proyectil alcanza la altura máxima su velocidad en este punto es cero. Teniendo en cuenta que el punto desde el que se lanza el proyectil es {y}_{o}=0 y la velocidad inicial es {v}_{o}=50 \mathrm{m}/\mathrm{s} , podemos calcular la altura final empleando la tercera ecuación.
Despejamos la altura final de la ecuación.
{v}_{f}^{2}={v}_{o}^{2}-2g\left({y}_{f}-{y}_{o}\right)\to -\frac{{v}_{f}^{2}-{v}_{o}^{2}}{2g}={y}_{f}-{y}_{o}
\therefore {y}_{f}={y}_{o}-\frac{{v}_{f}^{2}-{v}_{o}^{2}}{2g}
Sustituimos en la ecuación.
{y}_{f}=0-\frac{0-{\left(50\right)}^{2}}{2\left(9.81\right)}=127.42 \mathrm{m}
La altura máxima que alcanza la bala es de 127.42 metros.
Concluimos el problema indicando como respuesta correcta al inciso c).
Reactivo 7
Determinar la magnitud de la fuerza que se aplica a un cuerpo cuya masa es de 2.0 kg y posee una aceleración de a=0.24\mathrm{m}/{\mathrm{s}}^{2} .
- 0.05N
- 0.08N
- 0.10N
- 0.48N
Solución:
Para resolver el problema, aplicamos la segunda ley de Newton. Esta ecuación es vectorial, pero vamos a utilizar el módulo de las magnitudes vectoriales.
\overrightarrow{F}=m\overrightarrow{a}\to F=ma
Sustituimos los valores de la masa y la aceleración:
F=\left(2\right)\left(0.24\right)=0.48 \mathrm{N}
La fuerza aplicada sobre el cuerpo tiene una magnitud de 0.48 Newtons.
La respuesta correcta es el inciso d).
Reactivo 8
El ángulo máximo de la pendiente de un plano inclinado de 2.2 m de altura y 4 m de base es tal que permite que un bloque de peso de 100 N repose en equilibrio, ¿cuál es el coeficiente de fricción estático entre el plano inclinado y el bloque?
- 18
- 25
- 45
- 55
Solución:
Realicemos un dibujo de la situación planteada en el enunciado.
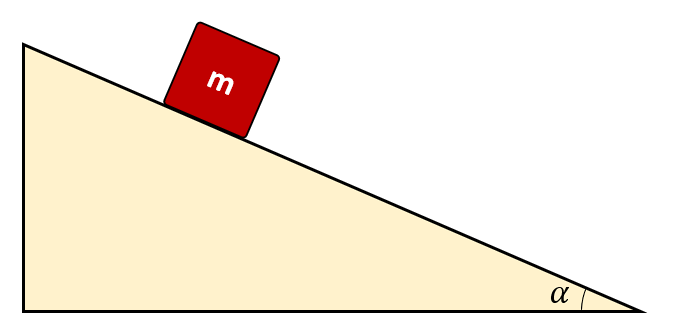
Debemos tener en cuenta que el plano inclinado posee fricción, cuyo valor es nuestra incógnita. Además, recordemos que la fuerza de roce es igual al producto del coeficiente de roce por la normal.
Aplicamos una descomposición de las fuerzas que actúan sobre el bloque mediante un diagrama de cuerpo libre.
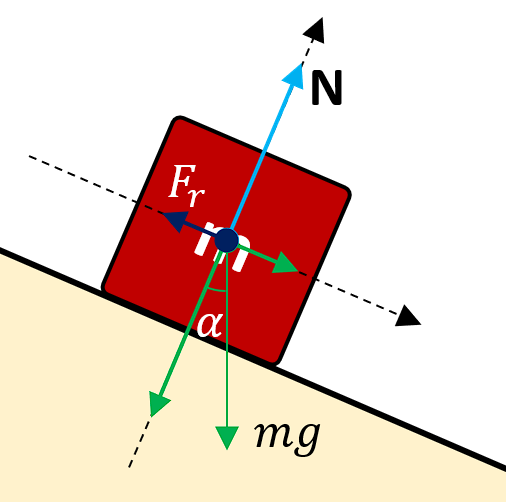
Descomponemos el peso en las componentes x y y .
{W}_{x}=mg\mathrm{sin}\alpha
{W}_{y}=-mg\mathrm{cos}\alpha
Ahora aplicamos la primera ley de Newton.
\begin{array}{c}{F}_{x}: mg\mathrm{sin}\alpha -{F}_{r}=0\\ {F}_{y}:N-mg\mathrm{cos}\alpha =0\end{array}
Despejamos el valor de la normal del balance de fuerzas en el eje vertical.
N=mg\mathrm{cos}\alpha
Sustituimos este resultado en la primera ecuación:
mg\mathrm{sin}\alpha -{F}_{r}=0\to mg\mathrm{sin}\alpha -\mu N=0
mg\mathrm{sin}\alpha =\mu mg\mathrm{cos}\alpha
Despejamos el coeficiente de fricción \mu .
\mu =\frac{\mathrm{sin}\alpha }{\mathrm{cos}\alpha }=\mathrm{tan}\alpha
Ahora, no conocemos el valor de \alpha pero si las dimensiones del plano inclinado. Podemos calcular la tangente de \alpha aplicando razones trigonométricas.
Recordemos que el enunciado indica que el bloque está situado en lo más alto del plano, por lo tanto, usamos las dimensiones del plano.
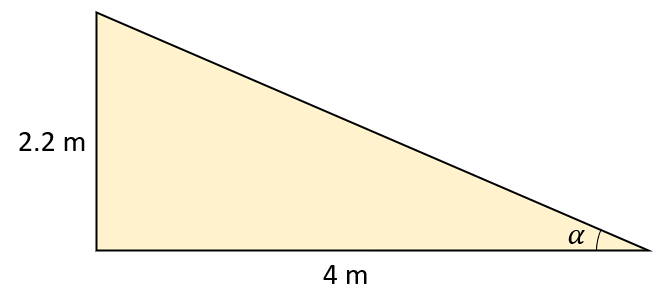
\mathrm{tan}\alpha =\frac{2.2}{4}=0.55
Otro razonamiento más general para justificar el uso de las dimensiones totales del bloque en el cálculo es que, sin importar la posición del bloque en el plano, todo triángulo que se formes será semejante, porque el ángulo \alpha es el mismo para todos.
Concluimos indicando que el coeficiente de fricción estático del plano es de 0.55 y que la respuesta correcta es el inciso d).
Reactivo 9
Una persona de 80 kg y otra persona de 90 kg están sentadas en una banca a una distancia de 60 cm. Calcular la magnitud de fuerza gravitacional que cada una ejerce sobre la otra considerando: \mathrm{G}=6.67\times {10}^{-11}\mathrm{N}\frac{{\mathrm{m}}^{2}}{{\mathrm{k}\mathrm{g}}^{2}}
- 6.6\times {10}^{-9}\mathrm{N}
- 7.0\times {10}^{-7}\mathrm{N}
- 1.3\times {10}^{-6}\mathrm{N}
- 5.0\times {10}^{-6}\mathrm{N}
Solución:
En este caso, aplicamos la ley de gravitación universal de Newton. La siguiente ecuación representa el módulo de la fuerza de atracción entre los cuerpos.
{F}_{12}=G\frac{{m}_{1}\cdot {m}_{2}}{{r}^{2}}
Convertimos la distancia a metros para sustituirla en la ecuación.
r=60 \mathrm{c}\mathrm{m}\cdot \frac{1 \mathrm{m}}{100 \mathrm{c}\mathrm{m}}=0.6 \mathrm{m}
Sustituimos todo en la ecuación:
{F}_{12}=\left(6.67\times {10}^{-11}\right)\frac{\left(80\right)\left(90\right)}{{\left(0.6\right)}^{2}}=1.334\times {10}^{-11} \mathrm{N}
El módulo de la fuerza de atracción entre las personas es de 1.334\times {10}^{-11} \mathrm{N} .
Comparando con los incisos, concluimos que la respuesta correcta es el inciso c).
Reactivo 10
Es uno de los llamados “problemas típicos” de rotación:
- cuerpos circundantes
- cuerpos rodantes
- estocásticos
- polímeros
Solución:
Tengamos en cuenta que “problemas típicos” se refiere a situaciones comunes que se resuelven en los ejercicios de rotación de los cuerpos.
Podemos descartar a los incisos c) y d), porque el primero se refiere a sistemas que dependen del azar para su desarrollo y el segundo a un tipo de sustancia química.
Por otra parte, “cuerpos circundantes” alude a un sistema físico en el que los elementos del sistema se rodean unos a otros, esto no es un problema de la rotación de los cuerpos. Por reducción, concluimos que la respuesta correcta es el inciso b).


