Guía IPN Sociales y Administrativas | Física reactivos 21 al 35

¡Hola de nuevo aspirante! Este es el ultimo post de la guía de física resuelta para la rama de CSA del IPN. No olvides visitar el resto de partes y desarrollar los ejercicios por tu cuenta, usa este material como apoyo ante dudas.

Parte II

Gestiona bien el tiempo y planifica las sesiones de estudio para cubrir todo el contenido del examen. [wpipa id=»6649″]

¿Qué viene en el examen del IPN?

El examen está dividido en dos partes: la primera con reactivos de matemáticas y comunicación, y la segunda con ejercicios de biología, química y física. La distribución de los 130 reactivos es la siguiente:

Guía IPN de Física resuelta

Accede a la solución paso a paso de los últimos 15 reactivos de física para CSA, a continuación. Aprobar el examen de ingreso es solo el inicio de tu carrera profesional, estudia con nosotros y asegúrate de entrar.

Reactivo 21: Escalas de temperatura

La escala Kelvin de temperatura se dice que es una escala:

1. Absoluta
2. Práctica
3. Energética
4. Dinámica

Solución:

Lord Kelvin propuso la construcción de una escala de temperatura cuyo cero fuese el cero absoluto, es decir, -273 °C y cuyos intervalos de un grado fueran iguales a los de la escala Centígrada, expresada como:

K=273°+C

Debido a que se encuentra referida al cero absoluto, se dice que la escala Kelvin es absoluta. Concluimos seleccionando como respuesta correcta la opción a).

Reactivo 22: Eficiencia de un Sistema Termodinámico

Una máquina toma 950 J de calor del reservorio de alta temperatura y tiene una eficiencia del 27%. ¿Qué cantidad de calor se expulsa al reservorio de baja temperatura?

1. 400.4 J
2. 565.3 J
3. 693.5 J
4. 714.8 J

Solución:

El rendimiento o eficiencia de una máquina termodinámica es la razón entre el trabajo neto o útil que realiza y la cantidad de calor que absorbe de un reservorio de alta temperatura.

\eta =\frac{{W}_{neto}}{{Q}_{abs}}

Donde:

• {W}_{neto} es el trabajo realizado por la máquina
• {Q}_{abs} es el calor absorbido

La imagen anterior muestra el funcionamiento básico de cualquier máquina termodinámica, donde el trabajo neto de salida puede expresarse como la resta del calor absorbido y el calor expulsado.

{W}_{neto}={Q}_{abs}-{Q}_{exp}

Sustituimos en la fórmula de eficiencia.

\eta =\frac{{Q}_{abs}-{Q}_{exp}}{{Q}_{abs}}=1-\frac{{Q}_{exp}}{{Q}_{abs}}

De esta expresión podemos despejar el calor expulsado por la máquina del enunciado.

{Q}_{exp}=\left(1-\eta \right){Q}_{abs}

Sustituimos los valores.

{Q}_{exp}=\left(1-0.27\right)\left(950 J\right)=693.5 J

El calor expulsado al reservorio de baja temperatura es de 693.5 Joules.

Seleccionamos como respuesta correcta a la opción c).

Reactivo 23: Interacciones eléctricas

La figura muestra dos cargas iguales; el patrón de líneas de campo corresponde a:

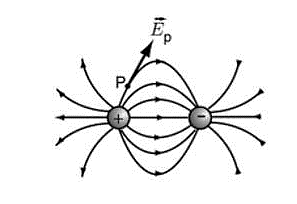
1. Un monopolo eléctrico
2. Una carga positiva
3. Un dipolo eléctrico
4. Una carga negativa

Solución:

Un dipolo eléctrico consiste en dos cargas opuestas, +q y -q , separadas por una distancia muy pequeña. En un dipolo eléctrico, las líneas de fuerza del campo van desde la carga positiva hacia la carga negativa, tal como se ejemplifica en la figura del problema.

Con esta simple explicación, concluimos entonces que la respuesta correcta es la opción c).

Reactivo 24: Intensidad del campo eléctrico

Al incrementar la distancia en la fórmula de campo eléctrico, ¿Qué le sucede a su magnitud?

1. Aumenta
2. Disminuye
3. Queda igual
4. Es independiente

Solución:

Recordemos que el campo eléctrico es generado por una carga eléctrica Q en algún punto del espacio y su intensidad depende de la fuerza eléctrica por unidad de carga de prueba q en cualquier punto del espacio donde se desee medir.

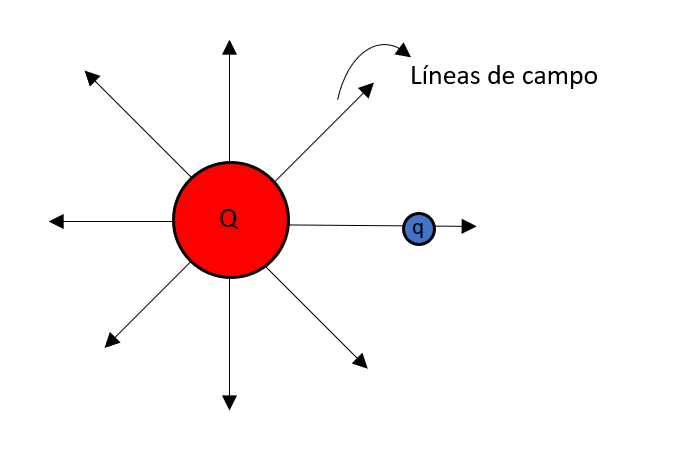
La fórmula para calcular la intensidad de campo eléctrico emitido por una carga en algún punto del espacio es inversamente proporcional al cuadrado de la distancia entre la carga Q y el punto de medición.

E=\frac{{K}_{e}Q}{{d}^{2}}

Es decir, para aumentos de la distancia la magnitud del campo eléctrico disminuye.

Concluimos seleccionando como respuesta correcta la opción b).

Reactivo 25: Campo eléctrico

Una fuerza eléctrica interactúa sobre un protón, el cual se encuentra situado en un punto donde experimenta una intensidad de campo eléctrico determinado. Ordenar en forma ascendente la magnitud de la fuerza que experimenta dicho protón considerando las diferentes magnitudes del campo eléctrico indicados a continuación.

1. 2\times {10}^{4}N/C
2. 1\times {10}^{5}N/C
3. 2\times {10}^{6}N/C
4. 1\times {10}^{8}N/C
5. 3\times {10}^{7}N/C

 

1. 3, 1, 4, 2, 5
2. 1, 2, 5, 3, 4
3. 3, 1, 5, 4, 2
4. 1, 2, 3, 5, 4

Solución:

Recordemos que la magnitud de la fuerza eléctrica que experimenta una partícula, en este caso un protón, es directamente proporcional al campo eléctrico que le rodea. Teniendo esto en cuenta, a mayor campo eléctrico mayor fuerza experimenta la partícula cargada.

A partir de este simple análisis podremos entonces ordenar de forma creciente las intensidades de campo eléctrico, que provocan de forma también creciente, una fuerza eléctrica sobre el protón.

2\times {10}^{4}N/C<1\times {10}^{5}N/C<2\times {10}^{6}N/C<3\times {10}^{7}N/C<1\times {10}^{8}N/C

Finalmente:

1, 2, 3, 5, 4

Comparando con las opciones, escogemos como correcta la d).

Reactivo 26: Longitud de onda

Calcular la longitud de onda del sonido de una sirena en reposo, cuya frecuencia senoidal es de 300 Hz, si la rapidez del sonido se considera de 340 m/s.

1. 5 m
2. 13 m
3. 88 m
4. 20 m

Solución:

La longitud de onda corresponde a la distancia que existe entre dos partículas consecutivas que se encuentran en fase sobre la onda, es decir, tienen la misma posición con respecto a su segmento de vibración. Se expresa mediante la letra griega \lambda  y su unidad en el S.I. es el metro.

Tenemos diferentes expresiones para calcular la longitud de onda, pero en este caso es útil la que relaciona la velocidad de propagación de la onda con su frecuencia.

\lambda =\frac{v}{f}

Sustituimos:

\lambda =\frac{340 m/s}{300 Hz}=1.13 m

Escogemos el inciso b) como la respuesta correcta.

Reactivo 27: Conceptos básicos de electrostática

Relacionar el concepto con su correspondiente modelo matemático.

1. 1C, 2A, 3D, 4B
2. 1D, 2A, 3C, 4B
3. 1C, 2B, 3A, 4D
4. 1D, 2C, 3B, 4A

Solución:

Para encontrar la combinación correcta, analizaremos cada uno de los conceptos de la columna izquierda para relacionarlo con el modelo matemático correcto en la columna derecha.

Constante de Coulomb.

Es una constante de equivalencia de unidades que se emplea en el cálculo de la fuerza de interacción entre cargas eléctricas. Cuando la distancia se mide en metros y la fuerza en Newtons, dicha constante {k}_{e} tiene un valor de 9\times {10}^{9}\frac{{Nm}^{2}}{{c}^{2}} .

Concluimos para este inciso: 1D.

Permitividad del vacío.

La permitividad eléctrica, mide la capacidad que tiene un material o sustancia a ser afectado por un campo eléctrico. Esta capacidad de polarización depende en gran medida de la composición molecular del material, su estructura y la susceptibilidad eléctrica del medio.

Para el vacío, la permitividad eléctrica se denota como {ϵ}_{o} y tiene un valor de 8.85\times {10}^{-12}\frac{{c}^{2}}{{Nm}^{2}} .

Concluimos entonces: 2C.

Fuerza de atracción entre dos cargas en el vacío.

La fuerza de interacción electrostática entre dos partículas cargadas es proporcional a sus cargas e inversamente proporcional al cuadrado de la distancia entre ellas. Esta definición recibe el nombre de Ley de Coulomb y en el vacío, la intensidad de dicha fuerza se calcula como:

F=\frac{k{q}_{1}{q}_{2}}{{r}^{2}}

Indicamos entonces que: 3B.

Distancia que separa a dos cargas que se atraen con una fuerza dada, en el vacío.

A partir de la Ley de Coulomb, podemos despejar la distancia entre dos cargas {q}_{1} y {q}_{2} , obteniendo la siguiente expresión:

d=\sqrt{\frac{k{q}_{1}{q}_{2}}{F}}

Finalmente: 4A.

Combinando todas las respuestas nos queda: 1D, 2C, 3B, 4A. Comparando con los incisos, la respuesta correcta se encuentra en el d).

Reactivo 28: Conceptos básicos de Circuitos Eléctricos

Relacionar el concepto con el modelo matemático.

1. 1C, 2D, 3A, 4B
2. 1C, 2B, 3D, 4A
3. 1D, 2C, 3A, 4B
4. 1D, 2A, 3B, 4C

Solución:

Procedemos a relacionar cada concepto de la columna izquierda con su respectivo modelo matemático en la columna derecha.

Ley de Ohm: R=\frac{V}{I}

1C.

Resistencia eléctrica: R=\rho \frac{L}{A}

2D.

Resistividad: \rho =\frac{RA}{L}

3A.

Unidad de la diferencia de potencial: \frac{1J}{1C}=1V

4B.

Antes de concluir, debemos aclarar la diferencia entre el inciso 1 y el 2. La ley de Ohm es una relación Volt-Ampere, es decir, es un modelo matemático del comportamiento de la resistencia como elemento circuital, a partir de las variables eléctricas corriente y voltaje.

Por otro lado, la Resistencia Eléctrica describe la propiedad que tienen los materiales al oponerse al paso de la corriente. Se relaciona con su forma geométrica (área y longitud) y con sus propiedades físicas (resistividad).

Finalmente, combinamos las respuestas obteniendo: 1C, 2D, 3A, 4B. Comparando con las opciones, la respuesta correcta es la a).

Reactivo 29: Resistencia equivalente

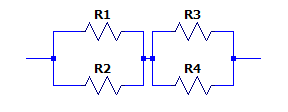
Si cada resistencia es de 1 \Omega  , identificar el arreglo de mayor resistencia total de los siguientes arreglos de resistencias.

1. 
2. 
3. 
4. 

Solución:

Para resolver este problema, debemos recordar que la resistencia equivalente (es decir, la resistencia total) es mayor cuando el arreglo es en serie y menor cuando es en paralelo. A mayor número de resistores en paralelo, menor es la equivalente y viceversa para el caso en serie.

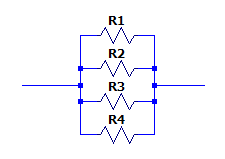
Teniendo en cuenta esto, podemos evitar realizar demasiados cálculos y descartar el inciso c) porque todas están en paralelo y, por ende, es el arreglo con menor resistencia equivalente. Procedemos a calcular el resto.

Arreglo del inciso a).

Tenemos dos pares de resistencias en paralelo y ambos arreglos conectados en serie. La equivalente es igual a:

{R}_{ea}={R}_{1}\left|\right|{R}_{2}+{R}_{3}\left|\right|{R}_{4}

Sustituyendo y realizando cálculos nos queda:

{R}_{ea}=\frac{\left(1 \Omega \right)\left(1 \Omega \right)}{1 \Omega +1 \Omega }+\frac{\left(1 \Omega \right)\left(1 \Omega \right)}{1 \Omega +1 \Omega }=1 \Omega 

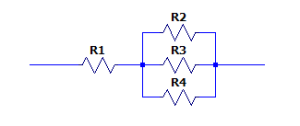
Arreglo del inciso b).

Una resistencia en serie con un paralelo de tres. La equivalente es igual a:

{R}_{eb}={R}_{1}+{R}_{2}\left|\left|{R}_{3}\right|\right|{R}_{4}

{R}_{eb}=1 \Omega +\frac{1}{\frac{1}{1 \Omega }+\frac{1}{1 \Omega }+\frac{1}{1 \Omega }}=1.33 \Omega 

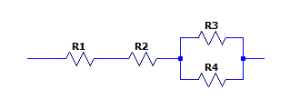
Arreglo del inciso d).

Un paralelo de dos resistencias en serie con dos resistencias simples. El equivalente es igual a:

{R}_{ed}={R}_{1}+{R}_{2}+{R}_{3}\left|\right|{R}_{4}

{R}_{ed}=1 \Omega +1 \Omega +\frac{\left(1 \Omega \right)\left(1 \Omega \right)}{1 \Omega +1 \Omega }=2.5 \Omega 

Comparando los resultados, el mayor de ellos es el d). La respuesta correcta al ejercicio es el inciso d).

Reactivo 30: Ley de Ohm

Determinar la intensidad de la corriente eléctrica en amperes, a través de una resistencia de 1k\Omega  , al aplicarle una diferencia de potencial de 120 V .

1. 12
2. 2
3. 0
4. 2

Solución:

En este caso, debemos aplicar la ley de Ohm:

R=\frac{V}{I}

Debido a que la resistencia R es conocida y el voltaje aplicado V también, despejamos a la corriente, sustituimos y calculamos.

R=\frac{V}{I}\to I=\frac{V}{R}

El prefijo “k” en el signo omega de la resistencia se utiliza para resumir una potencia de 10 elevada a 3, es decir: 1 K\Omega =1\times {10}^{3} \Omega  . Sustituimos en la fórmula:

I=\frac{120 V}{1\times {10}^{3} \Omega }=0.12 A

Por el resistor circula una corriente de 0.12 amperios.

La respuesta correcta es la opción a).

Reactivo 31: Potencia eléctrica

Por una parrilla eléctrica circula una corriente de 3 A, al estar conectada a una diferencia de potencial de 120 V. Determinar la resistencia eléctrica que tiene, potencia que desarrolla y el calor que produce en un minuto.

R ( \Omega  ), P (W), Q (J)

1. 120, 2400, 970760
2. 120, 3440, 77680
3. 40, 300, 68760
4. 40, 360, 21600

Solución:

La resistencia eléctrica de la parrilla se calcula a partir de la ley de Ohm:

R=\frac{V}{I}

Sustituimos el voltaje aplicado 120 V y la corriente que circula por la parrilla, 3 A.

R=\frac{120 V}{3 A}=40 \Omega 

Por otro lado, la potencia se calcula como el producto de la corriente por el voltaje aplicado:

P=VI=\left(120 V\right)\left(3 A\right)=360 W

Finalmente, el calor desarrollado por la parrilla se calcula como el producto de la potencia y el intervalo de tiempo dado, en este caso 1 minuto o 60 segundos.

Q=P\bullet \Delta t=\left(360 W\right)\left(60 s\right)=21600 J

Concluimos entonces:

R=40 \Omega ;P=360 W;Q=21600 J

Comparando con las opciones, la respuesta correcta es el inciso d).

Reactivo 32: Ley de Ohm

Un circuito eléctrico está conectado a una pila de 12 V. La intensidad de la corriente es de 2 A. Calcular la resistencia que ofrece el circuito al paso de la corriente.

1. 5.8 \Omega
2. 6.0 \Omega
3. 6.3 \Omega
4. 6.5 \Omega

Solución:

La resistencia equivalente del circuito eléctrico puede calcularse aplicando la ley de Ohm:

{R}_{c}=\frac{V}{I}

En este caso, el voltaje en terminales es de 12 V y la intensidad de la corriente 2 A. Sustituimos ambos valores y los evaluamos.

{R}_{c}=\frac{12 V}{2 A}=6 \Omega 

Concluimos indicando al inciso b) como la respuesta correcta.

Reactivo 33: Circuitos eléctricos

En el circuito mostrado {R}_{A}>{R}_{B} :

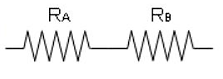
Seleccionar las ecuaciones aplicables.

1. {V}_{A}={V}_{B}; {I}_{A}={I}_{B}
2. {V}_{A}>{V}_{B}{ I}_{A}>{I}_{B}
3. {V}_{A}={V}_{B} {I}_{A}<{l}_{B}
4. {V}_{A}>{V}_{B}{ I}_{A}={I}_{B}

Solución:

Debido a que están conectadas en serie, ambas resistencias poseen la misma corriente, por tanto, podemos indicar:

{I}_{A}={I}_{B}=I

Ahora, según la ley de Ohm podemos expresar la caída de tensión en cada resistencia como:

{V}_{A}={R}_{A}I

{V}_{B}={R}_{B}I

Ya que la corriente es igual, el voltaje en cada resistencia depende de su valor resistivo. Como {R}_{A} es mayor que {R}_{B} , el producto {R}_{A}I es mayor que {R}_{B}I . Concluimos que: la caída de tensión en {R}_{A} es mayor que en {R}_{B} .

{V}_{A}>{V}_{B}

Las ecuaciones que aplican para este caso son:

{V}_{A}>{V}_{B}; {I}_{A}={I}_{B}

La respuesta correcta es el inciso d).

Reactivo 34: Amperímetro

Calcular la resistencia del resistor de derivación que convierta a un amperímetro de 2 mA con resistencia de 100 \Omega  a un amperímetro que de una desviación de escala completa con 1 A.

1. 0.2\Omega
2. 0.4\Omega
3. 0.6\Omega
4. 0.8\Omega

Solución:

Debido a que los amperímetros están fabricados en base a un galvanómetro, el cual es un dispositivo que permite medir corrientes muy pequeñas, necesita que se le acople en paralelo una resistencia de derivación o resistencia shunt, para medir corrientes más grandes.

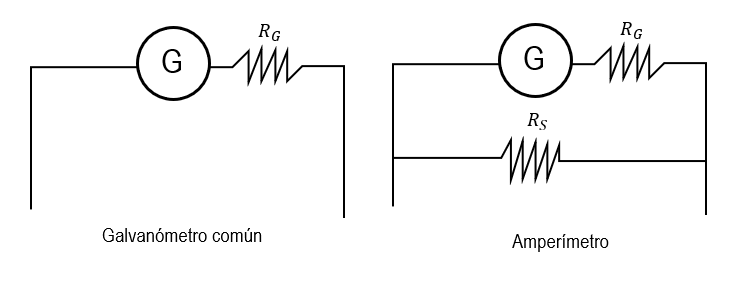
Si aplicamos la Ley de Corrientes de Kirchhoff al nodo de conexión, la corriente de medición se divide entre el galvanómetro y la resistencia de derivación.

i={i}_{S}+{i}_{G}

En este caso, conocemos la corriente máxima que deseamos medir: 1 A, y la corriente para máxima deflexión en dicha condición: 2 mA. Nuestra incógnita es la resistencia shunt que podemos expresar como:

{i}_{S}=\frac{V}{{R}_{S}}

Sustituyendo.

i=\frac{V}{{R}_{S}}+{i}_{G}\to {R}_{S}=\frac{V}{i-{i}_{G}}

Ahora tenemos una nueva incógnita: el voltaje en terminales de {R}_{S} . Como el galvanómetro y {R}_{S} están en paralelo tienen el mismo voltaje y, además, sabemos que corriente atraviesa a la resistencia del galvanómetro, por tanto, por ley de Ohm podemos conseguir su voltaje y, por ende, el voltaje en {R}_{S} .

V={i}_{G}{R}_{G}\to {R}_{S}=\frac{{i}_{G}{R}_{G}}{i-{i}_{G}}

Sustituimos los valores numéricos en la ecuación.

{R}_{S}=\frac{\left(0.002 A\right)\left(100 \Omega \right)}{1 A-0.002 A}=0.2 \Omega 

La resistencia de derivación debe ser de 0.2 \Omega  .

Concluimos indicando como respuesta correcta la opción a).

Reactivo 35: Arreglos de capacitores

Relacionar cada enunciado con el arreglo de capacitores que corresponde.

1. 1C, 2A
2. 1B, 2A
3. 1C, 2B
4. 1A, 2C

Solución:

Para responder esta pregunta correctamente, debemos recordar lo que sucede cuando se conectan condensadores en serie y en paralelo.

En un arreglo en serie, la magnitud de la carga q en las placas de cada condensador debe ser la misma. Si encerramos en un recuadro punteado las placas de dos condensadores contiguos, la carga neta debe ser cero. Una placa tiene +q de carga y la otra -q de carga.

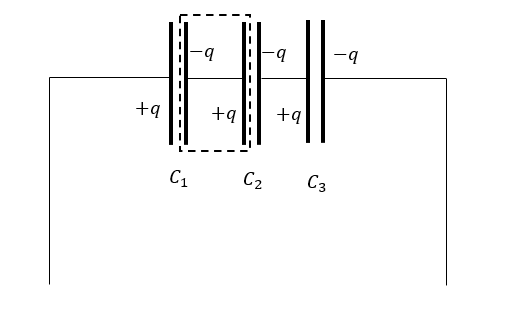
Como consecuencia de esto, la capacidad equivalente del arreglo se calcula como:

{C}_{eq}=\frac{1}{{\sum }_{}^{}\frac{1}{{C}_{i}}}

Equivalente que es siempre menor al más pequeño de los capacitores.

Por otra parte, los capacitores en paralelo poseen igual potencial, pero la carga eléctrica se divide proporcionalmente según la capacidad de cada condensador. Aplicando un poco de álgebra, encontraremos que la capacidad equivalente en paralelo es igual a la suma de las capacidades.

{C}_{eq}={\sum }_{}^{}{C}_{i}

{C}_{eq} es mayor que el capacitor más grande del arreglo.

Procedemos a relacionar ambas columnas:

1C, 2A.

Comparando con las opciones, la respuesta correcta es la a).