Llegamos a la segunda y última parte de la guía de física para el área de Ciencias Sociales y Administrativas, reactivos desde el 11 al 25 de la guía de estudio IPN 2023.

El siguiente es un resumen de la convocatoria IPN.
- Carreras ofertadas en IPN: 70+.
- Porcentaje de Aceptación: 20%.
- Preguntas en el examen de Admisión: 140 preguntas.
- Nuevos temas: historia e inglés (reading comprehension).
- Tipo: selección múltiple.
Llegamos al final de la guía de física, aspirante. Puedes continuar estudiando el resto de asignaturas en la sección de materiales IPN.
Reactivo 11
Desde el reposo, una pluma de ave cae dentro de un tubo de vacío a una altura de 12 m sobre la superficie de la tierra. ¿Cuál de las siguientes afirmaciones es correcta en relación con este fenómeno?
- La velocidad máxima de la pluma es de 9.8 m/s
- La aceleración de la pluma aumenta durante la caída
- La aceleración de la pluma permanece constante durante la trayectoria
- La aceleración de la pluma disminuye hasta que se alcanza la velocidad terminal
Solución:
Cuando describimos el movimiento que experimentan los cuerpos en caída libre, se desprecia la interacción de los cuerpos con el viento. Esto se hace, porque dicha interacción se manifiesta como una fuerza que frena al cuerpo durante la caída y cuyo cálculo es bastante complejo.
Recordamos lo anterior, porque en el enunciado se menciona que la pluma se deja caer en un tubo al vacío, precisamente para despreciar el efecto del aire. Cuando un objeto cae libremente, experimenta una única fuerza: el peso.
Dicha interacción está relacionada con la masa del cuerpo y es la responsable de acelerar al mismo hacia el centro de la tierra. La interacción gravitatoria entre la pluma y la tierra es la responsable de esta interacción.
Por esta razón, la aceleración que experimentan todos los cuerpos en la tierra es constante y vale aproximadamente 9.81\frac{\mathrm{m}}{{\mathrm{s}}^{2}} . Teniendo en cuenta todo lo anterior y examinando los incisos, concluimos que la respuesta correcta es c).
Reactivo 12
Determinar el tiempo que tarda en regresar un objeto de 1 kg que es lanzado desde el suelo con una rapidez de 5 m/s. Considerar g=10\mathrm{m}/{\mathrm{s}}^{2} .
- 0.5 \mathrm{s}
- 1.0 \mathrm{s}
- 3.4 \mathrm{s}
- 6.5 \mathrm{s}
Solución:
Este es un problema de lanzamiento vertical hacia arriba. Iniciemos mencionando que siempre se desprecia el efecto del viento y que el movimiento es simétrico: de subida y bajada. Esto nos permite calcular el tiempo de vuelo como dos veces el tiempo de la altura máxima.
{t}_{v}=2{t}_{Max}
El tiempo de la altura máxima, ocurre cuando la velocidad del proyectil es igual a 0 \mathrm{m}/\mathrm{s} .
{v}_{fy}={v}_{oy}-gt\to {v}_{o}-gt=0
\therefore {t}_{\mathrm{M}\mathrm{a}\mathrm{x}}=\frac{{v}_{o}}{g}
El tiempo de vuelo sería:
{t}_{v}=2\frac{{v}_{o}}{g}
Evaluamos y calculamos.
{t}_{v}=2\frac{5}{10}=1 \mathrm{s}
El cuerpo tarda un segundo en subir y bajar cuando se lanza verticalmente hacia arriba con una velocidad inicial de 5 m/s. La respuesta correcta es el inciso b).
Conoce los pasos para aplicar a la universidad: Todo sobre la convocatoria del IPN.
Reactivo 13
Una bola de metal de 110 N se encuentra suspendida del cordel A, es tirada hacia un lado por otro cordel B y mantenida de tal forma que entre el cordel A y la pared vertical se forma un ángulo de 35°. Encontrar las tensiones de los cordeles A y B.
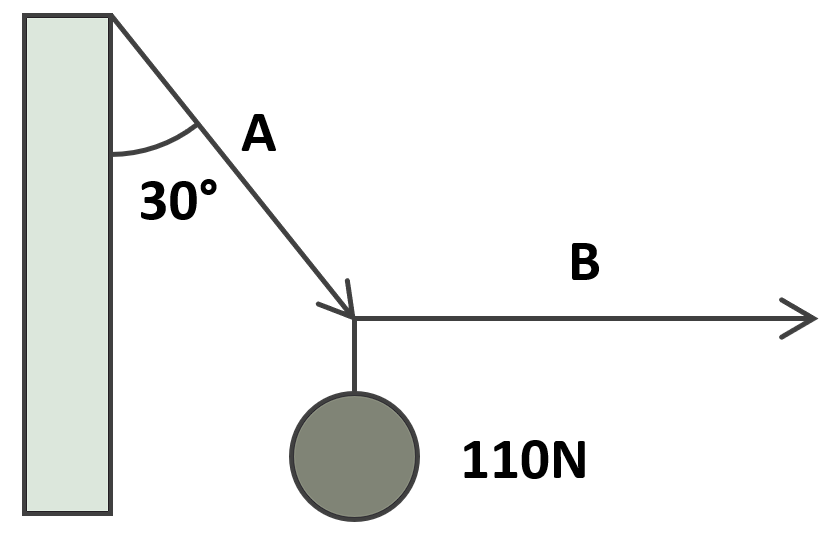
- {T}_{A}=86.6\mathrm{N},{T}_{B}=200\mathrm{N}
- {T}_{A}=127.02\mathrm{N},{T}_{B}=63.5\mathrm{N}
- {T}_{A}=135.47\mathrm{N},{T}_{B}=57.73\mathrm{N}
- {T}_{A}=257.73\mathrm{N},{T}_{B}=115.47\mathrm{N}
Solución:
Para calcular la magnitud de las fuerzas, debemos realizar el diagrama de cuerpo libre respecto al punto en el que se unen las cuerdas.
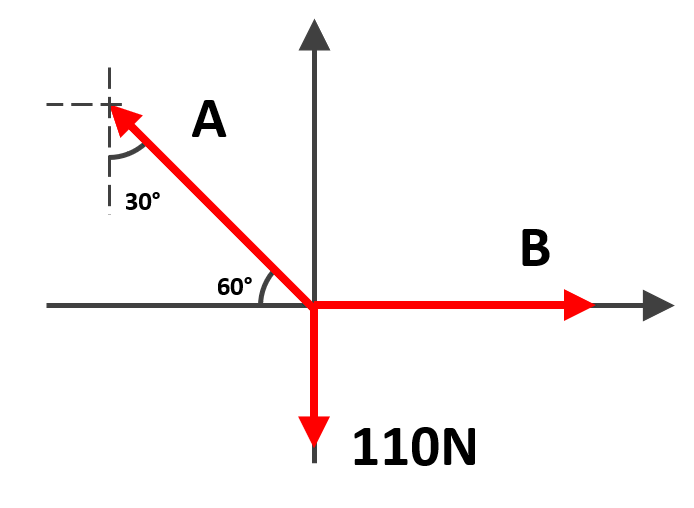
Cuando hacemos el diagrama de cuerpo libre en la unión de las cuerdas, la tensión de la cuerda A se manifiesta tirando hacia el bloque, tal como se indica en el diagrama. Por otro lado, el ángulo de 30° respecto a la vertical del vector tensión A, se traslada como un ángulo de 60° respecto a la horizontal.
Descomponiendo las fuerzas nos queda:
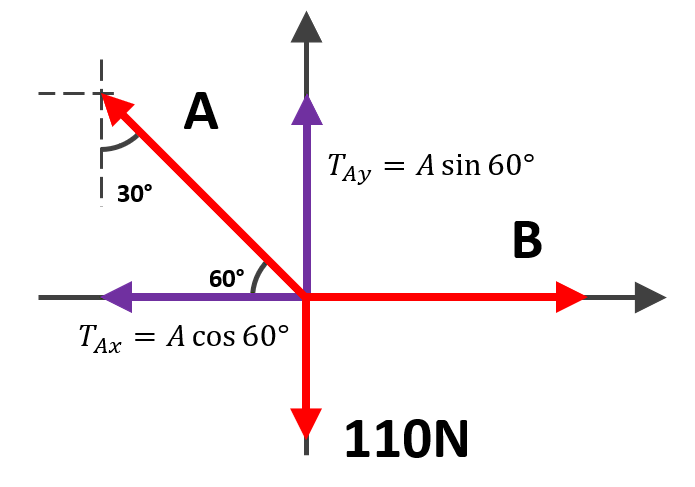
Aplicamos la primera Ley de Newton.
\begin{array}{c}{F}_{x}:{T}_{B}-{T}_{A}\mathrm{cos}60°=0\\ {F}_{y}:{T}_{A}\mathrm{sin}60°-110=0\end{array}
Despejamos la magnitud de la fuerza {T}_{A} de la segunda ecuación.
{T}_{A}=\frac{110}{\mathrm{sin}60°}=127.02 \mathrm{N}
Calculamos la magnitud de la fuerza {T}_{B} .
{T}_{B}={T}_{A}\mathrm{cos}60°=\left(127.02\right)\mathrm{cos}60°=63.5 \mathrm{N}
Finalmente:
{T}_{A}=127.02 \mathrm{N},\mathrm{ }{T}_{B}=63.5 \mathrm{N}
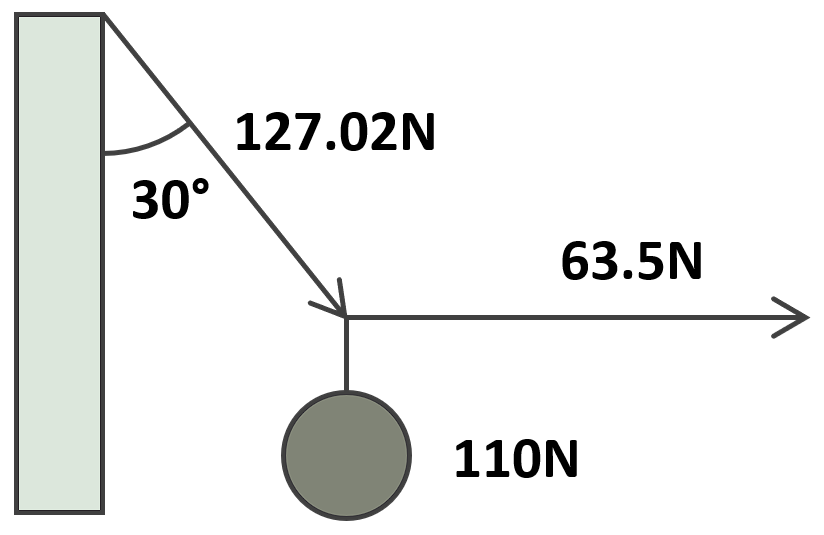
Concluimos que la respuesta correcta es el inciso b).
Reactivo 14
Una pelota de golf de 45 g que se mueve con una rapidez de 16 m/s golpea un auto en movimiento, lo que causa que rebote en dirección contraria a una velocidad de 76 m/s. Determinar la magnitud de la fuerza media ejercida sobre el auto, si la pelota durante el impacto estuvo en contacto con él 1 ms.
- 720 N
- 3420 N
- 4140 N
- 5510 N
Solución:
Para resolver este problema, empleamos la segunda ley de Newton expresada en función a la variación de momento lineal.
\overrightarrow{F}=\frac{\mathrm{\Delta }\overrightarrow{p}}{\mathrm{\Delta }t}
Si el momento lineal es igual a p=mv , la ecuación anterior nos queda:
\overrightarrow{F}=\frac{\mathrm{\Delta }\overrightarrow{p}}{\mathrm{\Delta }t}=\frac{m\left({\overrightarrow{v}}_{2}-{\overrightarrow{v}}_{1}\right)}{\mathrm{\Delta }t}
A partir del enunciado, sabemos que la velocidad 1 es {\overrightarrow{v}}_{1}=16\frac{\mathrm{m}}{\mathrm{s}}\left(\widehat{i}\right) , mientras que la velocidad 2 es {\overrightarrow{v}}_{2}=-76\frac{\mathrm{m}}{\mathrm{s}}\left(\widehat{i}\right) . Lleva el signo negativo porque la pelota rebota en dirección contraria. Por otra parte, hemos supuesto que el movimiento es unidimensional.
Sustituimos en la ecuación. La masa debe estar en kilogramos y el intervalo de tiempo en segundos.
m=45\mathrm{g}=0.045\mathrm{ }\mathrm{k}\mathrm{g}
\mathrm{\Delta }t=1 \mathrm{m}\mathrm{s}=0.001\mathrm{ }s
Finalmente:
\overrightarrow{F}=\frac{\left(0.045\right)\left(-76-16\right)}{0.001}\left(\widehat{i}\right)=-4140\left(\widehat{i}\right) \mathrm{N}
Finalmente, la magnitud de la fuerza media ejercida sobre el auto es de 4140 N.
La respuesta correcta es el inciso c).
Conoce la oferta académica completa del Instituto Politécnico Nacional: Lista de carreras del IPN por área.
Reactivo 15
Calcular la fuerza que se aplica a un resorte si este tiene una constante elástica de 130 N/m y se alargó 20 cm.
- 13 N
- 18 N
- 20 N
- 26 N
Solución:
La fuerza elástica producida por un resorte se calcula aplicando la ley de Hooke.
{F}_{e}=-k\mathrm{\Delta }x
Donde k es la constante elástica del resorte y \mathrm{\Delta }x la deformación que experimenta. Transformamos la deformación a metros y la sustituimos en la ecuación.
\mathrm{\Delta }x=20 \mathrm{c}\mathrm{m}\cdot \frac{1 \mathrm{m}}{100 \mathrm{c}\mathrm{m}}=0.2 \mathrm{m}
Finalmente:
{F}_{e}=-\left(130\right)\left(0.2\right)=-26 \mathrm{N}
Ahora, esta es la fuerza que produce el resorte. La fuerza aplicada por el resorte se calcula aplicando la tercera Ley de Newton.
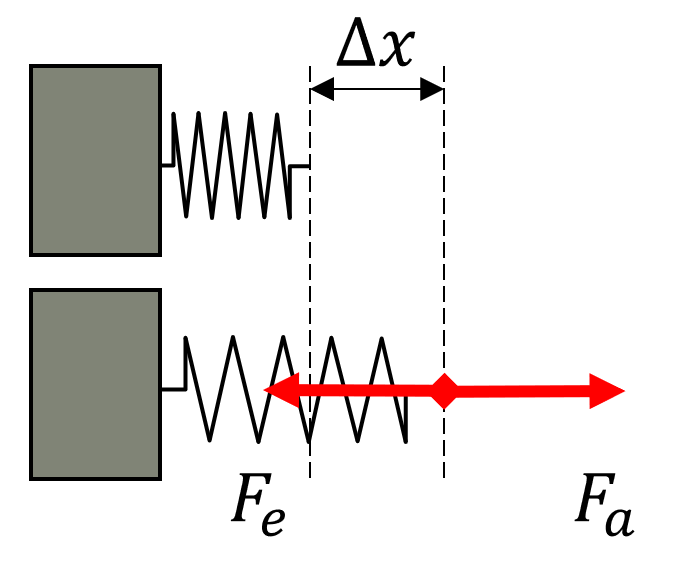
{F}_{a}=-{F}_{e}\to {F}_{a}=-\left(-26\right)
\therefore {F}_{a}=26 \mathrm{N}
La respuesta correcta es el inciso d).
Reactivo 16
Determinar el calor que se produce en un conductor cuya resistencia es de 40 ohmios y por el que corre una corriente eléctrica de 1.8 A en un tiempo de 30 segundos.
- 0.342 kJ
- 1.170 kJ
- 1.640 kJ
- 3.888 kJ
Solución:
Para calcular el calor irradiado por el resistor, primero determinamos la potencia disipada aplicando la siguiente ecuación:
{P}_{R}=R\cdot {i}^{2}
Esta ecuación nos da la potencia en Joules/segundos, debemos multiplicar por los 30 segundos para obtener la energía total disipada.
{E}_{d}=R\cdot {i}^{2}\cdot \mathrm{\Delta }t
Sustituimos.
{E}_{d}=R\cdot {i}^{2}\cdot \mathrm{\Delta }t=\left(40\right){\left(1.8\right)}^{2}\left(30\right)
\therefore {E}_{d}=3888 \mathrm{J}
Expresado en notación de ingeniería:
{E}_{d}=3.888 \mathrm{k}\mathrm{J}
Indicamos como respuesta correcta al inciso d).
¿Sabes cuántos puntos necesitas para quedar? Conoce los aciertos por carrera del IPN.
Reactivo 17
Determinar la frecuencia de las ondas que se transmiten por una cuerda tensa, cuya velocidad de propagación es de 300 m/s y su longitud de onda es de 0.8 m.
- f=274.7 \mathrm{H}\mathrm{z}
- f=285 \mathrm{H}\mathrm{z}
- f=289.71\mathrm{H}\mathrm{z}
- f=375 \mathrm{H}\mathrm{z}
Solución:
Empleamos la ecuación que relaciona a la frecuencia, velocidad de propagación y longitud de una onda.
v=\lambda \cdot f
Despejamos a la frecuencia.
f=\frac{v}{\lambda }
Sustituimos y simplificamos.
f=\frac{300}{0.8}=375 \mathrm{H}\mathrm{z}
La frecuencia de las ondas que se propagan en la cuerda tensada es de 375 Hertz.
Concluimos seleccionando como respuesta correcta al inciso d).
Reactivo 18
Una onda ___ es aquella que presenta un movimiento de partículas perpendicular a la dirección de propagación de la misma onda.
- armónica
- mecánica
- transversal
- longitudinal
Solución:
Las ondas pueden propagarse en un medio, de dos posibles formas: longitudinalmente o transversalmente. Las ondas longitudinales oscilan en la dirección de propagación, mientras que las transversales oscilan perpendicularmente a la dirección de propagación.
Teniendo esto en cuenta, el inciso que completa correctamente al enunciado es el c).
Una onda transversal es aquella que presenta un movimiento de partículas perpendiculares a la dirección de propagación de la misma onda.
Reactivo 19
Ordenar de manera descendente y de acuerdo con la magnitud de la velocidad del sonido los siguientes medios a 0°C.
- Hidrógeno
- Aluminio
- Agua
- Aire
- 4, 3, 2, 1
- 2, 1, 4, 3
- 4, 1, 3, 2
- 2, 3, 1, 4
Solución:
Esta pregunta se puede responder de forma analítica, recurriendo a las ecuaciones o conociendo la velocidad del sonido en estos medios cuando T=0°C . En este caso, vamos a aplicar un análisis partiendo de la ecuación para calcular la velocidad de las ondas mecánicas en un medio.
v=\sqrt{\frac{\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{p}\mathrm{i}\mathrm{e}\mathrm{d}\mathrm{a}\mathrm{d}\mathrm{ }\mathrm{e}\mathrm{l}\mathrm{á}\mathrm{s}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{a}}{\mathrm{p}\mathrm{r}\mathrm{o}\mathrm{p}\mathrm{i}\mathrm{e}\mathrm{d}\mathrm{a}\mathrm{d}\mathrm{ }\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{r}\mathrm{c}\mathrm{i}\mathrm{a}\mathrm{l}}}
Cuando un medio es más denso y, por ende, posee mayor rigidez, el sonido se propaga más rápido debido a que a mayor rigidez más difícil de comprimir se vuelve el medio.
Partiendo de esta premisa, el medio donde el sonido se mueve más rápido es el aluminio. De los cuatro medios, es el que mayor densidad y rigidez posee. Le sigue el agua, luego va el hidrógeno y finalmente el aire. Entre el aire y el hidrógeno, este último posee mayor densidad entre los dos.
2, 3, 1, 4.
La respuesta correcta es el inciso d).
Reactivo 20
Un automóvil que se mueve a 20 m/s haciendo sonar su claxon ( f=1200 \mathrm{H}\mathrm{z} ), persigue a otro automóvil que se mueve a una velocidad de 15 m/s. ¿Cuál es la frecuencia aparente del claxon escuchada por el conductor perseguido? Considerar la rapidez del sonido como 340 m/s.
- 1219 Hz
- 886 Hz
- 560 Hz
- 45Hz
Solución:
Debemos aplicar la fórmula del efecto Doppler para resolver el problema. Primero debemos identificar a la fuente y luego a la velocidad relativa de la fuente respecto del receptor.
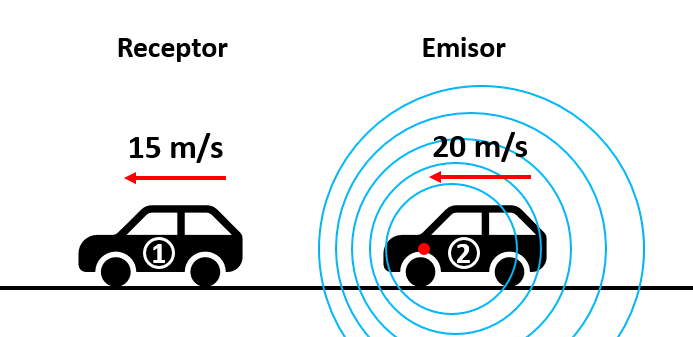
La velocidad del emisor es de 20 m/s mientras que la del receptor es de 15 m/s. La velocidad relativa u del emisor respecto al receptor es:
u=20-15=5 \mathrm{m}/\mathrm{s}
f={f}_{0}\frac{{v}_{m}}{{v}_{m}\mp u}
Donde {f}_{o} es la frecuencia original de la onda y {v}_{m} es la velocidad de las ondas en el medio. En este caso: {f}_{o}=1200\mathrm{ }\mathrm{H}\mathrm{z} y {v}_{m}=340 \mathrm{m}/\mathrm{s} . La velocidad relativa u es negativa cuando la fuente se acerca al receptor y positiva cuando se aleja. Sustituimos.
f=\left(1200\right)\frac{340}{340-5}=\left(1200\right)\frac{340}{335}=\left(1200\right)\left(1.015\right)
f=\left(1200\right)\left(1.015\right)=1218 \mathrm{H}\mathrm{z}
La frecuencia de la onda percibida desde el receptor es de 1218 Hertz.
Seleccionamos como respuesta correcta al inciso a).
Reactivo 21
¿Qué voltaje se mide en un circuito si este tiene una resistencia de 1800 \mathrm{\Omega } y una corriente de 300 mA?
- 75000 V
- 30000 V
- 7500 V
- 540V
Solución:
Para calcular la tensión en terminales de la resistencia, empleamos la ley de Ohm.
R=\frac{V}{I}
Despejamos al voltaje.
V=I\cdot R
Antes de sustituir, transformamos la corriente de mA a A.
I=300 \mathrm{m}\mathrm{A}=300\times {10}^{-3} \mathrm{A}=0.3\mathrm{ }\mathrm{A}
Finalmente:
V=\left(0.3\right)\left(1800\right)=540 \mathrm{V}
La tensión en terminales de la resistencia es igual a 540 voltios.
La respuesta correcta es el inciso d).
Reactivo 22
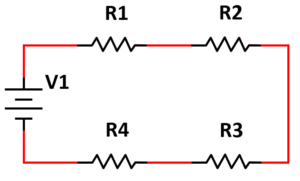
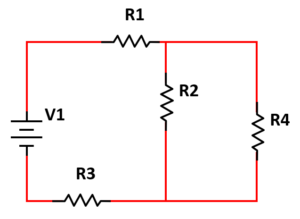
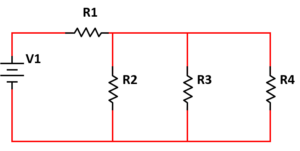
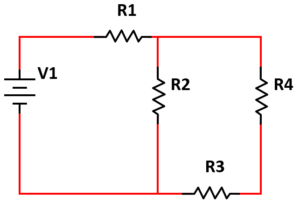
Elegir el tipo de circuito resistivo que se obtiene al realizar los siguientes pasos.
- Conectar una terminal de la resistencia R1 al positivo de la batería.
- En serie a la resistencia R1, conectar la resistencia R2.
- En serie a la resistencia R2, conectar la resistencia R3.
- Conectar la terminal libre de R3 al negativo de la batería.
- Paralelo a la resistencia R2, conectar la resistencia R4.
Solución:
Para encontrar el circuito equivalente, debemos construir el circuito a partir de la descripción dada por el enunciado.
Conectar una terminal de la resistencia R1 al positivo de la batería.
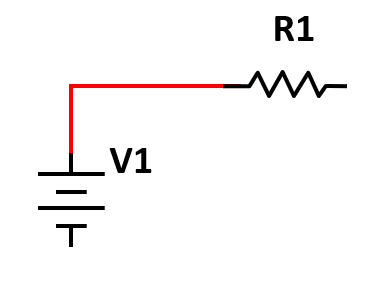
Recordemos que el terminal positivo de la batería es el que tiene el extremo más largo.
En serie a la resistencia R1, conectar la resistencia R2.
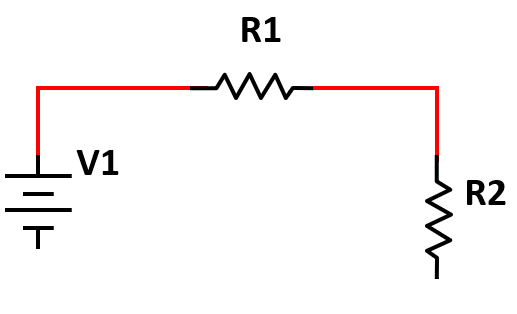
En serie a la resistencia R2, conectar la resistencia R3.
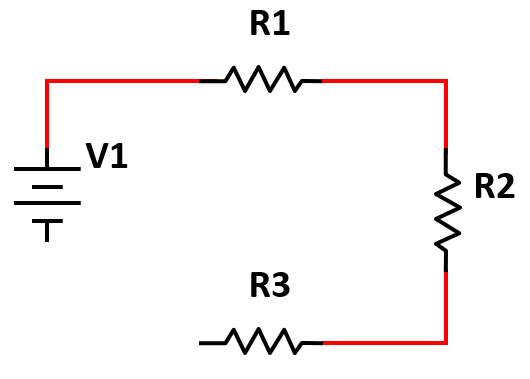
Conectar la terminal libre de R3 al negativo de la batería.
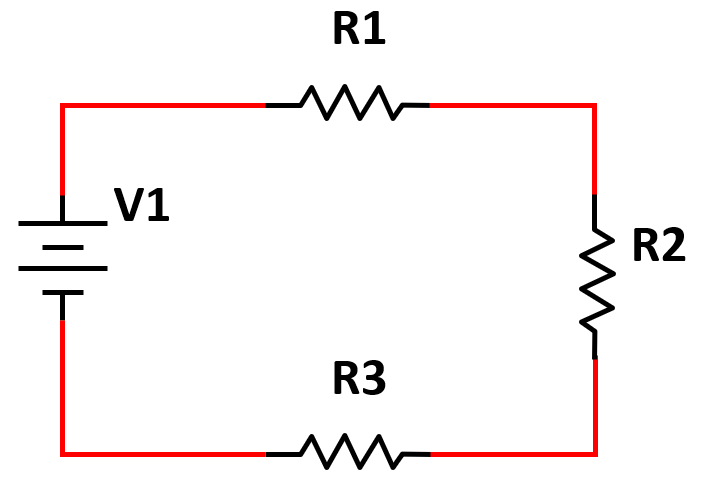
Paralelo a la resistencia R2, conectar la resistencia R4.
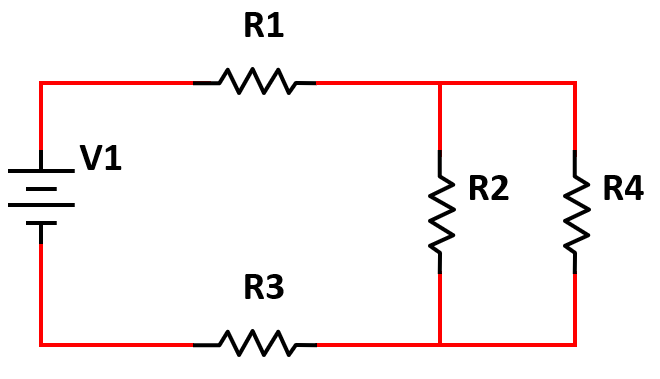
Concluimos el reactivo seleccionando como respuesta correcta al inciso b).
Reactivo 23
En un imán, las zonas de mayor interacción con otros materiales se denominan _______, pero se identifican como _________ y ________ por convención.
- lados – positivo – negativo
- polos – positivo – neutro
- extremos – norte – sur
- polos – norte – sur
Solución:
Las regiones de un imán en las que se concentra la mayor cantidad de líneas de campo llevan el nombre de polos magnéticos. El extremo por el que salen las líneas de campo se llama polo norte y por el que entran se llama polo sur.
Teniendo esto en cuenta:
En un imán, las zonas de mayor interacción con otros materiales se denominan polos, pero se identifican como norte y sur por convención.
La respuesta correcta es el inciso d).
Reactivo 24
La región del espacio donde se pone de manifiesto la acción de un imán se llama campo magnético y se representa mediante líneas:
- perpendiculares al campo magnético
- rectas tangentes al campo magnético
- cerradas y que van del polo norte al polo sur
- cerradas y que van del polo sur al polo norte
Solución:
En electromagnetismo, se utiliza el concepto de líneas de fuerza para la representación gráfica de los campos eléctrico y magnético. En el caso del campo magnético, las líneas de fuerza son cerradas y van desde el polo norte y cierran en el polo sur.
Considerando lo anterior y examinando a los incisos, concluimos que el c) contiene la respuesta correcta.
Reactivo 25
Relacionar el método de magnetización con su característica.

- 1A, 2B, 3C
- 1B, 2C, 3A
- 1A, 2C, 3B
- 1B, 2A, 3C
Solución:
Debemos relacionar los métodos enumerados en la columna izquierda, con sus correspondientes definiciones indicadas en la columna derecha.
Iniciamos con el método de magnetización por contacto. Examinando la columna derecha, vemos que corresponde con la definición en el inciso B.
Magnetización por contacto: Consiste en permitir que un extremo del material a magnetizar haga contacto permanente con el polo de un imán.
En este caso: 1B. Descartamos los incisos a y c. El método de magnetización por frotamiento es definido en el inciso C.
Magnetización por frotamiento: Consiste en friccionar el material con el polo de un imán en una sola dirección.
Para el inciso: 2C. Con esta información: 1B, 2C, … tenemos información suficiente para concluir que la respuesta correcta es la opción b).