Continúa con la solución de la segunda parte de la guía de física para el área de Ciencias Médico Biológicas, como preparación a la prueba de ingreso al IPN.
Tómate el tiempo necesario para comprender los conceptos básicos y domina física ¡Cómo todo un pro!
Conoce el curso que cubre todos los temas del nuevo examen de ingreso al IPN con clases en vivo y exámenes simulacro.
Reactivo 11
Calcular la temperatura final de una masa de hierro de 200 g cuya temperatura inicial es de 27 °C y absorbe 2000 cal. El calor específico del hierro es de 0.113 cal/g °C.
- 40.2°C
- 843°C
- 10.28 °C
- 115.5°C
Solución:
El calor específico de una sustancia es una magnitud física que cuantifica la cantidad de calor que se debe aplicar a un sistema termodinámico para elevar su temperatura.
c=\frac{Q}{m\cdot \mathrm{\Delta }T}
En este caso particular, la energía no se encuentra expresada en Joules, sino en calorías. No es necesario hacer alguna conversión, porque el enunciado indica la energía absorbida por el cuerpo en calorías.
Despejamos a la variación de temperatura.
c=\frac{Q}{m\cdot \mathrm{\Delta }T}\to \mathrm{\Delta }T=\frac{Q}{m\cdot c}
Sustituimos a la variación de temperatura como {T}_{2}-{T}_{1} .
{T}_{2}-{T}_{1}=\frac{Q}{m\cdot c}
Despejamos a la temperatura final {T}_{2} .
{T}_{2}=\frac{Q}{m\cdot c}+{T}_{1}
Sustituimos los valores.
{T}_{2}=\frac{2000 \mathrm{c}\mathrm{a}\mathrm{l}}{200\mathrm{ }\mathrm{g}\cdot 0.113\frac{\mathrm{c}\mathrm{a}\mathrm{l}}{\mathrm{g}\mathrm{ }°\mathrm{C}}}+27=88.5+27
{T}_{2}=115.5 °C
La temperatura final de la masa de hierro es de 115.5 grados Celsius.
Escogemos como respuesta correcta al inciso d).
Reactivo 12
Un bloque de cobre (\mathrm{k}=385\mathrm{W}/(\mathrm{m}\mathrm{K}\left)\right) tiene una sección transversal de 20{\mathrm{c}\mathrm{m}}^{2} y una longitud de 50 cm. El extremo izquierdo se mantiene a 0 K y el derecho a 100 K. ¿Cuál es la razón del flujo de calor en watts?
- 207 W
- 178 W
- 154 W
- 131 W
Solución:
Para resolver el problema, debemos aplicar la ley de Fourier para el flujo de calor.
{\phi }_{q}=k\frac{\mathrm{\Delta }T}{\mathrm{\Delta }x}
Donde k es la conductividad térmica del material, \mathrm{\Delta }T es la variación de temperatura y \mathrm{\Delta }x el intervalo de longitud en el que ocurre la variación de temperatura.
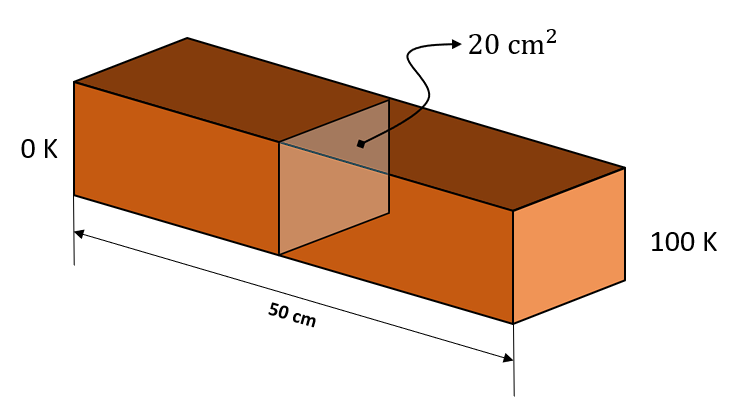
El enunciado nos dice que la conductividad térmica del bloque de cobre es 385\frac{\mathrm{W}}{\mathrm{m}\cdot \mathrm{K}} . La variación de temperatura es de 100 Kelvin y la variación de longitud es de 50 cm o 0.05 metros.
Sustituimos en la ecuación para obtener el flujo de calor por unidad de área.
{\phi }_{q}=\left(385\frac{\mathrm{W}}{\mathrm{m}\cdot \mathrm{K}}\right)\frac{100 \mathrm{K}-0}{0.5\mathrm{ }\mathrm{m}-0}=77000\frac{\mathrm{W}}{{\mathrm{m}}^{2}}
Ahora, debemos multiplicar por el área de sección transversal del bloque. Transformamos de cm cuadrados a metros cuadrados.
20{\mathrm{c}\mathrm{m}}^{2}=0.002 {\mathrm{m}}^{2}
Finalmente:
{W}_{q}=\left(77000\frac{\mathrm{W}}{{\mathrm{m}}^{2}}\right)\left(0.002 {\mathrm{m}}^{2}\right)=154 \mathrm{W}\mathrm{a}\mathrm{t}\mathrm{t}\mathrm{s}
La razón de cambio de calor en el bloque es igual a 154 Watts.
La respuesta correcta es el inciso c).
Reactivo 13
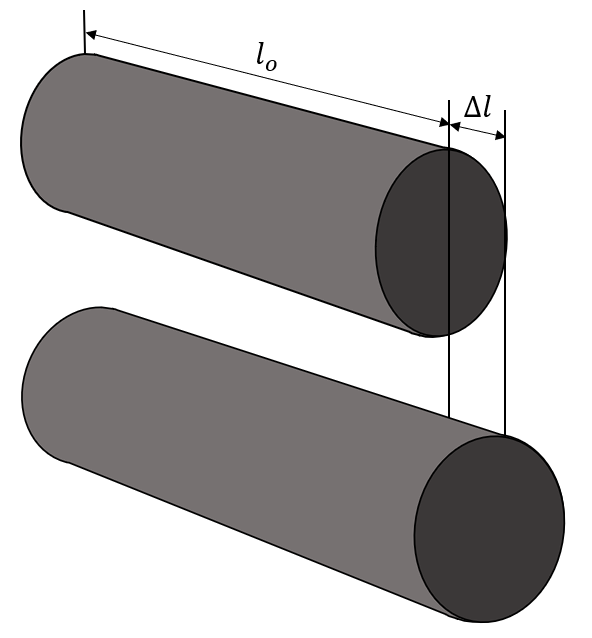
Un trozo de tubo de cobre \alpha =1.7\times {10}^{-5}/°\mathrm{C} tiene 6 m de longitud a 20°C. ¿Cuánto incrementará su longitud cuando se caliente a 80°C?
- 3.18mm
- 6.12cm
- 3.18cm
- 6.12mm
Solución:
En este problema debemos utilizar las ecuaciones relacionadas con la dilatación térmica en los sólidos. En líneas generales, la dilatación térmica de los sólidos se clasifica en función al número de dimensiones en las que se manifiesta: lineal, superficial y volumétrica.
Analizando el enunciado, queda claro que la dilatación térmica ocurre de forma longitudinal. El incremento de longitud por dilatación térmica se calcula como:
\mathrm{\Delta }{l}^{\text{'}}={l}_{o}\cdot \alpha \cdot \mathrm{\Delta }T
Donde \alpha es el coeficiente de dilatación térmica, \mathrm{\Delta }T es la variación de temperatura y {l}_{o} es la longitud inicial del tubo. Según el enunciado:
\alpha =1.7\times {10}^{-5}/°\mathrm{C}
{l}_{o}=6 \mathrm{m}
{T}_{1}=20°C
{T}_{2}=80°C
Evaluamos.
\mathrm{\Delta }{l}^{\text{'}}=\left(6 \mathrm{m}\right)\cdot \left(1.7\times {10}^{-5}\frac{1}{°C}\right)\cdot \left(80-20\right)=0.00612 \mathrm{m}
Expresado en milímetros:
\mathrm{\Delta }{l}^{\text{'}}=6.12 \mathrm{m}\mathrm{m}
La respuesta correcta es el inciso d).
Reactivo 14
Determinar el incremento en la energía interna de un sistema si cede 800 calorías de calor y se le aplica un trabajo de 1000 Joules. Considerar que 1 caloría es igual a 4.20 J.
- -900 J
- -2360 J
- 3840 J
- 7680 J
Solución:
El cambio de la energía interna de un sistema cerrado se calcula como:
\mathrm{\Delta }U=W+Q
Tengamos en cuenta que el calor y el trabajo son positivos cuando entran al sistema, pero negativos cuando son generados o emitidos por el sistema termodinámico.
Convertimos el calor a Joules.
800 \mathrm{c}\mathrm{a}\mathrm{l}\cdot \frac{4.20 \mathrm{J}}{1 \mathrm{c}\mathrm{a}\mathrm{l}}=3360 \mathrm{J}
Sustituimos el calor negativo (el sistema emite calor) y el trabajo positivo (porque se aplica sobre el sistema).
\mathrm{\Delta }U=-3360+1000=-2360 \mathrm{J}\mathrm{o}\mathrm{u}\mathrm{l}\mathrm{e}\mathrm{s}
Finalmente, indicamos como respuesta correcta al inciso b).
Reactivo 15
La _______ de una onda es el proceso por el cual esta puede oscilar en más de una orientación.
- polarización
- refracción
- difracción
- reflexión
Solución:
La característica descrita en el enunciado se denomina polarización y es la cualidad que poseen las ondas electromagnéticas al oscilar en ángulos distintos.
Esto aplica para sus dos componentes: campo eléctrico y campo magnético. La respuesta correcta es el inciso a).
La polarización de una onda es el proceso por el cual esta puede oscilar en más de una orientación.
Reactivo 16
¿Qué nombre recibe la parte de la onda señalada en la imagen?
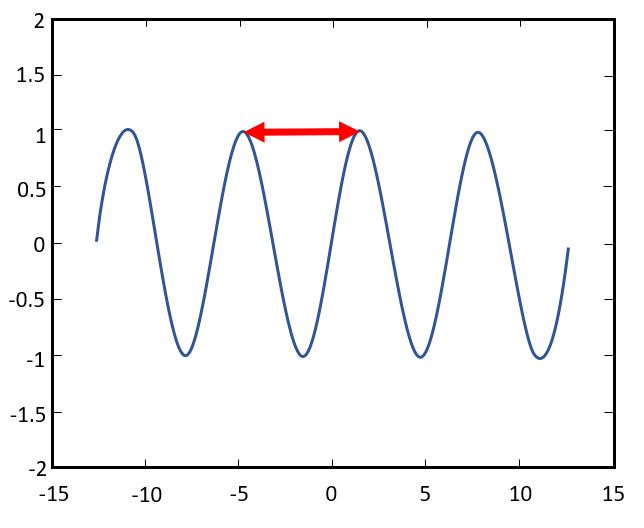
- Valle
- Nodo
- Cresta
- Longitud de onda
Solución:
La distancia entre dos valles o crestas consecutivas de una onda sinusoidal se conoce como la longitud de onda de la oscilación. La respuesta correcta es el inciso d).
Reactivo 17
¿Cuál es la velocidad a la que se propaga una onda longitudinal en un resorte, cuando su frecuencia es de 200 Hz y su longitud de onda es \lambda =0.9\mathrm{m} ?
- v=144\frac{\mathrm{m}}{\mathrm{s}}
- v=146\frac{\mathrm{m}}{\mathrm{s}}
- v=148\frac{\mathrm{m}}{\mathrm{s}}
- v=180\frac{\mathrm{m}}{\mathrm{s}}
Solución:
Para resolver el problema, debemos utilizar la ecuación de velocidad de propagación de una onda.
v=\lambda \cdot f
Sustituimos.
v=\left(0.9\right)\left(200\right)=180\frac{\mathrm{m}}{\mathrm{s}}
Concluimos que la respuesta correcta es el inciso d).
Reactivo 18
Calcular la velocidad del sonido en el aire cuando su masa molecular es 29\times {10}^{-3}\mathrm{k}\mathrm{g}/\mathrm{m}\mathrm{o}\mathrm{l} y la temperatura ambiente es 27°C. Considerar la constante adiabática de 1.4 y R = constante universal de gases = 8.314 J/mol.K.
- 344\mathrm{m}/\mathrm{s}
- 344\mathrm{k}\mathrm{m}/\mathrm{h}
- 347\mathrm{k}\mathrm{m}/\mathrm{h}
- 347\mathrm{m}/\mathrm{s}
Solución:
Para calcular la velocidad del sonido en un medio gaseoso, empleamos la ecuación:
v=\sqrt{\frac{\gamma RT}{M}}
Donde:
- \gamma es la constante de dilatación adiabática
- R es la constante universal de los gases en \frac{\mathrm{J}}{\mathrm{k}\mathrm{g} \mathrm{K}}
- M es la masa molar del gas
- T es la temperatura en Kelvin
El resultado de la ecuación es la velocidad en metros por segundo. Transformamos la temperatura de Celsius a Kelvin.
T=27°C+273.5=300.15 \mathrm{K}
Sustituimos en la ecuación:
v=\sqrt{\frac{\left(1.4\right)\left(8.314\right)\left(300.15\right)}{29\times {10}^{-3}}}=347 \mathrm{m}/\mathrm{s}
La respuesta correcta es el inciso d).
Materiales de estudio
Reactivo 19
A través de un telescopio ubicado en la Tierra, se observa la radiación electromagnética de una estrella. Esta última se aleja de la Tierra con una rapidez de 0.600 c. Existe un efecto Doppler en la frecuencia de la radiación debido al movimiento de la estrella, el cual puede calcularse mediante la expresión:
f={f}_{0}\sqrt{\left(\right(c-u)/(c+u\left)\right)}
Donde c es la velocidad de la luz; u , la rapidez con la que se aleja la estrella y {f}_{0} la frecuencia de radiación. Si la radiación tiene una frecuencia de 8.64\times {10}^{14}\mathrm{H}\mathrm{z} , en el marco en reposo de la estrella, ¿cuál es la frecuencia medida por un observador desde la Tierra?
- 9.64\times {10}^{14}\mathrm{H}\mathrm{z}
- 6.24\times {10}^{14}\mathrm{H}\mathrm{z}
- 5.46\times {10}^{14}\mathrm{H}\mathrm{z}
- 4.32\times {10}^{14}\mathrm{H}\mathrm{z}
Solución:
En líneas generales, el efecto Doppler es un fenómeno ondulatorio en el que la frecuencia de una onda emitida desde una fuente, parece ser modificada cuando existe un movimiento relativo entre un receptor y el emisor en cuestión.
En este caso, estamos midiendo el cambio de la frecuencia de la radiación emitida por la estrella debido a su movimiento relativo respecto de la tierra. El enunciado establece que la velocidad relativa entre la tierra y la estrella es de 0.6 veces la velocidad de la luz: u=0.6c .
Debido a que la estrella se aleja de la tierra, la velocidad relativa u es negativa:
u=-0.6c
Mientras que la frecuencia de la onda emitida desde la estrella es de 8.64\times {10}^{14}\mathrm{H}\mathrm{z} . Sustituimos todo en la ecuación dada.
f=\frac{{f}_{o}}{\sqrt{\frac{c-u}{c+u}}}=\frac{{f}_{o}}{\sqrt{\frac{c+0.6c}{c-0.6c}}}=\frac{{f}_{o}}{\sqrt{\frac{1.6}{0.4}}}=\frac{1}{\sqrt{4}}{f}_{o}=\frac{{f}_{o}}{2}
Finalmente:
f=\frac{8.64\times {10}^{14}\mathrm{H}\mathrm{z}}{2}=4.32\times {10}^{14}\mathrm{H}\mathrm{z}
La frecuencia de la onda electromagnética que se recibe en la tierra, respecto a la estrella es de 4.32\times {10}^{14}\mathrm{H}\mathrm{z} .
Indicamos como respuesta correcta al inciso d).
Reactivo 20
Determinar la resistencia de una plancha si está conectada a una línea de 130 V y tiene una corriente de 20 A.
- 1.5\mathrm{\Omega }
- 3\mathrm{\Omega }
- 6.5\mathrm{\Omega }
- 9\mathrm{\Omega }
Solución:
Empleamos la Ley de Ohm para calcular la resistencia de la plancha.
R=\frac{V}{I}
Sustituimos.
R=\frac{130}{20}=6.5 \mathrm{\Omega }
La plancha tiene una resistencia eléctrica de 6.5 Ohm.
Seleccionamos como respuesta correcta al inciso c).
