¡Felicidades, aspirante! Llegamos a la tercera y última parte de la guía de física para el área de CMB, como preparación al examen de ingreso del poderosísimo IPN.

Reactivo 21
Calcular la fuerza que produce una carga de +20\mu \mathrm{C} sobre otra de -30\mu \mathrm{C} , cuando esta última se encuentra a 30 cm de la primera. La constante de Coulomb es: K={9.10}^{9}\frac{{\mathrm{N}\mathrm{m}}^{2}}{{\mathrm{C}}^{2}} .
- 252 N
- 60 N
- -60 N
- -70 N
Solución:
Para calcular la fuerza eléctrica de atracción entre las cargas del enunciado, empleamos la Ley de Coulomb:
\overrightarrow{{F}_{e}}=\frac{k{q}_{1}{q}_{2}}{{d}^{2}}\overrightarrow{u}
Esta ecuación es vectorial, supondremos que la dirección en la que actúa la fuerza entre las cargas es lineal. Sustituimos los valores, teniendo en cuenta el signo de las cargas. La distancia expresada en metros es de 0.3 \mathrm{m} .
\overrightarrow{{F}_{e}}=\frac{\left(9\times {10}^{9}\frac{{\mathrm{N}\mathrm{m}}^{2}}{{\mathrm{C}}^{2}}\right)\left(+20\mu \mathrm{C}\right)\left(-30\mu \mathrm{C}\right)}{{\left(0.3 \mathrm{m}\right)}^{2}}\left(\widehat{i}\right)
Los submúltiplos \mu se sustituyen por {10}^{-6} .
\overrightarrow{{F}_{e}}=\frac{\left(9\times {10}^{9}\frac{{\mathrm{N}\mathrm{m}}^{2}}{{\mathrm{C}}^{2}}\right)\left(+20\times {10}^{-6}\mathrm{C}\right)\left(-30\times {10}^{-6}\mathrm{C}\right)}{{\left(0.3 \mathrm{m}\right)}^{2}}\left(\widehat{i}\right)
Evaluamos.
\overrightarrow{{F}_{e}}=\frac{-5.4\mathrm{ }{\mathrm{N}\mathrm{m}}^{2}}{0.09 {\mathrm{m}}^{2}}\left(\widehat{i}\right)=-60 \mathrm{N}\left(\widehat{i}\right)
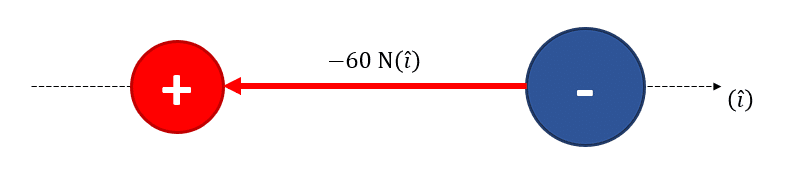
La respuesta correcta es el inciso c).
Reactivo 22
Un calentador eléctrico tiene una resistencia de 22\mathrm{\Omega } y utiliza una corriente de 5 A. Señalar el voltaje que produce este aparato.
- 85 V
- 95 V
- 100 V
- 110 V
Solución:
Aplicando la ley de Ohm:
R=\frac{V}{I}
Despejamos el voltaje en terminales del calentador.
V=RI
Evaluamos:
V=\left(22\right)\left(5\right)=110 \mathrm{V}
La tensión en terminales del calentador es igual a 110 voltios.
Seleccionamos como respuesta correcta al inciso d).
Reactivo 23
La resistencia de una bobina de alambre de cobre es de 3\mathrm{\Omega } a 20 °C. ¿Cuál es su resistencia a 50 °C? Para el cobre considerar: \alpha =3.9\times {10}^{-3}/°\mathrm{C} .
- 4.221\mathrm{\Omega }
- 3.351\mathrm{\Omega }
- 2.251\mathrm{\Omega }
- 1.111\mathrm{\Omega }
Solución:
Empleamos la ecuación de la resistencia eléctrica en función de la temperatura.
R={R}_{o}\left(1+\alpha \mathrm{\Delta }T\right)
La variación de temperatura es:
\mathrm{\Delta }T=50-20=30°C
Evaluamos la expresión:
R=\left(3\mathrm{\Omega }\right)\left[1+\left(3.9\times {10}^{-3}\frac{1}{°\mathrm{C}}\right)\left(30°\mathrm{C}\right)\right]
R=3\left(1+0.117\right)=3.351 \mathrm{\Omega }
La resistencia de la bobina es de 3.351 Ohm a 50°C.
Indicamos como respuesta correcta al inciso b).
Continúa practicando fisica:
Reactivo 24
Determinar la resistencia total {\mathrm{R}}_{\mathrm{T}} del siguiente circuito:
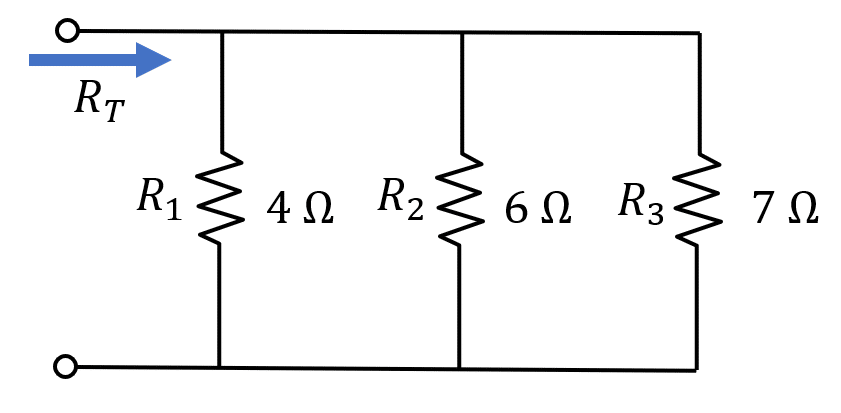
- 4.530\mathrm{\Omega }
- 3.530\mathrm{\Omega }
- 2.053\mathrm{\Omega }
- 1.787\mathrm{\Omega }
Solución:
La resistencia equivalente se obtiene al resolver el arreglo en paralelo de los tres resistores. La ecuación de resistores en paralelo quedaría:
{R}_{T}=\frac{1}{\frac{1}{{R}_{1}}+\frac{1}{{R}_{2}}+\frac{1}{{R}_{3}}}
Sustituimos y resolvemos.
{R}_{T}=\frac{1}{\frac{1}{4}+\frac{1}{6}+\frac{1}{7}}=\frac{1}{\frac{5}{12}+\frac{1}{7}}=\frac{1}{\frac{47}{84}}=\frac{84}{47}
Finalmente:
{R}_{T}=1.787 \mathrm{\Omega }
La resistencia total del arreglo en paralelo es de 1.787 \mathrm{\Omega } .
La respuesta correcta es el inciso d).
Reactivo 25
Se tienen 3 resistores conectados en paralelo con resistencias de 10\mathrm{\Omega },25\mathrm{\Omega }\text{ y }30\mathrm{\Omega } . Determinar la resistencia equivalente del sistema.
- 4.77\mathrm{\Omega }
- 5.77\mathrm{\Omega }
- 7.77\mathrm{\Omega }
- 8.77\mathrm{\Omega }
Solución:
La representación en circuito eléctrico de la situación planteada en el enunciado es:
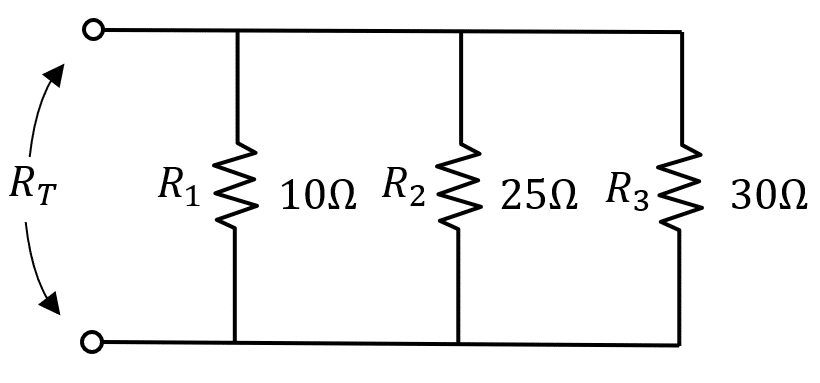
La resistencia total se calcula como:
{R}_{T}=\frac{1}{\frac{1}{{R}_{1}}+\frac{1}{{R}_{2}}+\frac{1}{{R}_{3}}}
Sustituimos y resolvemos.
{R}_{T}=\frac{1}{\frac{1}{10}+\frac{1}{25}+\frac{1}{30}}=\frac{1}{\frac{13}{75}}=\frac{75}{13}
Finalmente:
{R}_{T}=5.77 \mathrm{\Omega }
Finalizamos indicando como respuesta correcta al inciso b).
Reactivo 26
Identificar en qué zona la interacción entre los imanes presenta la mayor intensidad.
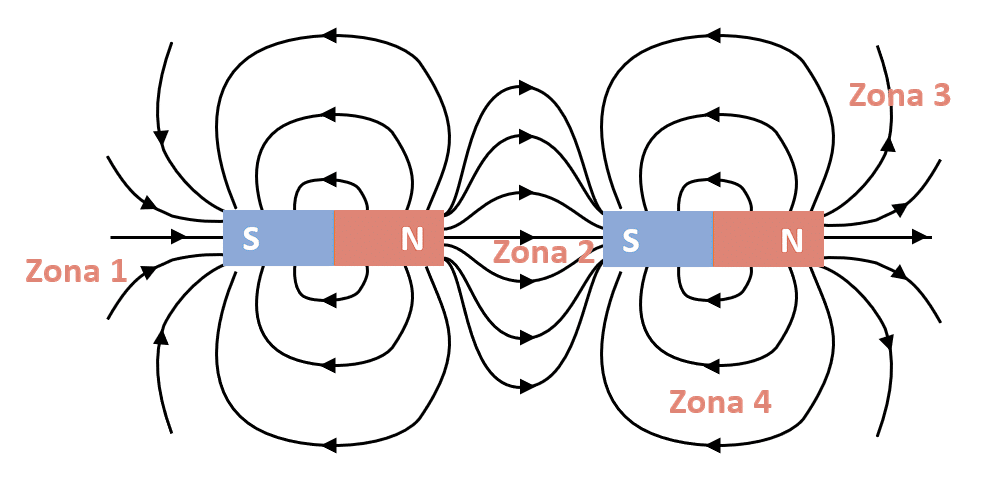
- 1
- 2
- 3
- 4
Solución:
Tanto en los imanes permanentes como en los electroimanes, las regiones con mayor flujo magnético y, por ende, con mayor intensidad de campo magnético se encuentran cerca de los polos.
En la figura se muestran a dos imanes permanentes, los cuales interactúan al enfrentar polos opuestos en el centro de la imagen. Dicha región se encuentra enumerada como zona 2 y es la que presenta la mayor intensidad en la interacción entre los imanes.
Hay que considerar que la fuerza magnética que se produce en la zona 2 es de atracción. Concluimos indicando como respuesta correcta al inciso b).
Reactivo 27
Relacionar el tipo de material con su principal característica:

- 1A, 2B, 3C
- 1C, 2A, 3B
- 1A, 2C, 3B
- 1C, 2B, 3A
Solución:
Debemos relacionar de forma correcta las clasificaciones de materiales en la columna izquierda, con las definiciones en la columna derecha. Iniciamos con los materiales diamagnéticos.
Los materiales diamagnéticos tienen la propiedad de oponerse a la presencia de un campo magnético. En este caso, sus dipolos magnéticos se alinean de forma contraria al flujo magnético externo, pero de forma muy débil. Por esto último, no se utilizan en la práctica para repeler campos magnéticos. En este caso: 1C. Descartamos los incisos a y c.
Los materiales paramagnéticos, son aquellos capaces de ser atraídos por campos magnéticos externos. Estos magnetizan sus dipolos magnéticos libres a favor del campo externo, pero la contribución total es débil y solo se mantiene con la presencia del campo externo. Asociamos en este caso: 2B.
Con esta información: 1C, 2B, … podemos concluir que la respuesta correcta es el inciso d).
Reactivo 28
¿Cómo se conoce a la fuerza calculada mediante la expresión \overrightarrow{F}=q(\overrightarrow{E}+\overrightarrow{v}x\overrightarrow{B}) ?
- Eléctrica
- Magnética
- De Tensión
- De Lorentz
Solución:
A esta expresión se le conoce como la Ley de Lorentz y permite calcular el vector fuerza que experimenta una partícula en movimiento dentro de un campo electromagnético. La respuesta correcta es el inciso d).
Reactivo 29
La ley de ________ establece que cualquier efecto de inducción tiende a oponerse al cambio que lo ocasiona.
- Lenz
- Gauss
- Ampere
- Faraday
Solución:
La ley de Faraday es una relación experimental que encontró el físico Michael Faraday al experimentar con bobinas y campos magnéticos.
Se dio cuenta que la tensión inducida en los terminales de una espira de alambre es directamente proporcional a la variación de flujo magnético que le atraviesa respecto del tiempo. Pero tenía un problema con su descripción: las agujas de los instrumentos indican tensiones negativas.
Tiempo después, el físico Heinrich Lenz estableció que la fuerza electromotriz inducida en una bobina es tal, que se opone a la variación del flujo magnético que le atraviesa. Por esta razón, las lecturas tienen signo contrario.
Todo esto se condensa en la Ley de Faraday-Lenz.
\mathrm{F}\mathrm{E}\mathrm{M}=-N\frac{d{\varphi }_{B}}{dt}
La respuesta correcta es el inciso a).
La ley de Lenz establece que cualquier efecto de inducción tiende a oponerse al cambio que lo ocasiona.
Reactivo 30
El proceso mediante el cual campos magnéticos generan campos eléctricos se conoce como ___ y se representa mediante un vector.
- inducción magnética
- inducción eléctrica
- fuerza magnética
- campo magnético
Solución:
La inducción magnética es el fenómeno físico que permite establecer una tensión en terminales de un circuito cuando fluye a través de él un flujo magnético que varía en el tiempo.
Este es el principio de funcionamiento de todas las máquinas eléctricas que permiten generar, transportar y distribuir la energía eléctrica hasta nuestros hogares. La respuesta correcta es el inciso a).
El proceso mediante el cual campos magnéticos generan campos eléctricos se conoce como inducción magnética y se representa mediante un vector.

