¡Continuamos, aspirante! Vamos con la solución de la guía de cálculo integral del IPN 2023. En este caso, vamos a desarrollar paso a paso los reactivos desde el 21 hasta el 30.

¿Se te ha complicado algún reactivo? ¡No te preocupes! En la mayoría de las soluciones mencionamos algunos de los hacks que explicamos en nuestras clases. Únete al curso y accede a contenido exclusivo.
Reactivo 21
Resolver la integral por partes:
\int {e}^{2x}\mathrm{cos}\left(3x\right)dx
- \frac{2}{13}{e}^{2x}\mathrm{cos}\left(3x\right)-\frac{3}{13}{e}^{2x}\mathrm{sin}\left(3x\right)
- \frac{3}{13}{e}^{2x}\mathrm{cos}\left(3x\right)-\frac{2}{13}{e}^{2x}\mathrm{sin}\left(3x\right)
- \frac{3}{13}{e}^{2x}\mathrm{cos}\left(3x\right)+\frac{2}{13}{e}^{2x}\mathrm{sin}\left(3x\right)+C
- \frac{2}{13}{e}^{2x}\mathrm{cos}\left(3x\right)+\frac{3}{13}{e}^{2x}\mathrm{sin}\left(3x\right)+C
Solución:
Examinando al integrando, no hay ninguna separación en factores que nos permita simplificar la integral. De hecho, esta integral por partes se denomina cíclica.
Porque nunca vamos a poder degradar a ninguna de las dos funciones, solo podemos continuar aplicando integración por partes hasta que obtengamos nuevamente la integral inicial. Según la fórmula de integración por partes:
\int udv=uv-\int vdu
En este primer ciclo, hacemos la selección:
u={e}^{2x}, dv=\mathrm{cos}\left(3x\right)dx
No vamos a desarrollar paso a paso las integrales intermedias, como la de \mathrm{cos}\left(3x\right) , porque en este punto debe ser un tema dominado.
du=2{e}^{2x}dx, v=\frac{1}{3}\mathrm{sin}\left(3x\right)
La integral nos queda:
\int {e}^{2x}\mathrm{cos}\left(3x\right)dx=\frac{1}{3}{e}^{2x}\mathrm{sin}\left(3x\right)-\frac{2}{3}\int {e}^{2x}\mathrm{sin}\left(3x\right)dx
Ahora, la nueva selección de u y dv se basa en el signo que necesitamos en la integral indicada que va a quedar. El signo debe ser negativo para que al pasarla al primer miembro se sume con la integral original.
Si hacemos dv=\mathrm{sin}\left(3x\right)dx , el resultado será negativo que, multiplicado por el negativo de la fórmula por partes queda positivo.
\int {e}^{2x}\mathrm{sin}\left(3x\right)dx=uv-\int \left(-\mathrm{cos}\left(3x\right)\right)du=uv+\int \mathrm{cos}\left(3x\right)du
Si ahora lo multiplicamos por el -\frac{2}{3} externo, nos queda negativo.
\int {e}^{2x}\mathrm{cos}\left(3x\right)dx=\frac{1}{3}{e}^{2x}\mathrm{sin}\left(3x\right)-\frac{2}{3}uv-\frac{2}{3}\int \mathrm{cos}\left(3x\right)du
Retomando:
\int {e}^{2x}\mathrm{cos}\left(3x\right)dx=\frac{1}{3}{e}^{2x}\mathrm{sin}\left(3x\right)-\frac{2}{3}\int {e}^{2x}\mathrm{sin}\left(3x\right)dx
En base al análisis anterior, para la segunda integral por partes escogemos: u={e}^{2x} y dv=\mathrm{sin}\left(3x\right)dx .
u={e}^{2x} y dv=\mathrm{sin}\left(3x\right)dx
du=2{e}^{2x}dx y v=-\frac{1}{3}\mathrm{cos}\left(3x\right)
Aplicando la fórmula por partes nos queda:
\int {e}^{2x}\mathrm{cos}\left(3x\right)dx=\frac{1}{3}{e}^{2x}\mathrm{sin}\left(3x\right)-\frac{2}{3}\left[-\frac{1}{3}{e}^{2x}\mathrm{cos}\left(3x\right)+\frac{2}{3}\int {e}^{2x}\mathrm{cos}\left(3x\right)dx\right]
Simplificamos:
\int {e}^{2x}\mathrm{cos}\left(3x\right)dx=\frac{1}{3}{e}^{2x}\mathrm{sin}\left(3x\right)+\frac{2}{9}{e}^{2x}\mathrm{cos}\left(3x\right)-\frac{4}{9}\int {e}^{2x}\mathrm{cos}\left(3x\right)dx
Rompemos el ciclo pasando la integral I=\int {e}^{2x}\mathrm{cos}\left(3x\right)dx al otro miembro.
I=\frac{1}{3}{e}^{2x}\mathrm{sin}\left(3x\right)+\frac{2}{9}{e}^{2x}\mathrm{cos}\left(3x\right)-\frac{4}{9}I
I+\frac{4}{9}I=\frac{1}{3}{e}^{2x}\mathrm{sin}\left(3x\right)+\frac{2}{9}{e}^{2x}\mathrm{cos}\left(3x\right)\to \frac{13}{9}I=\frac{1}{3}{e}^{2x}\mathrm{sin}\left(3x\right)+\frac{2}{9}{e}^{2x}\mathrm{cos}\left(3x\right)
Despejamos.
\frac{13}{9}I=\frac{1}{3}{e}^{2x}\mathrm{sin}\left(3x\right)+\frac{2}{9}{e}^{2x}\mathrm{cos}\left(3x\right)\to I=\frac{3}{13}{e}^{2x}\mathrm{sin}\left(3x\right)+\frac{2}{13}{e}^{2x}\mathrm{cos}\left(3x\right)
Finalmente:
\int {e}^{2x}\mathrm{cos}\left(3x\right)dx=\frac{3}{13}{e}^{2x}\mathrm{sin}\left(3x\right)+\frac{2}{13}{e}^{2x}\mathrm{cos}\left(3x\right)
La respuesta correcta es el inciso d). Aunque el procedimiento sea extenso y parezca confuso, debes concentrarte en identificar la selección de variables más conveniente al momento de la solución.
Reactivo 22
Identificar u y dv para realizar la integral:
\int {\mathrm{sec}}^{3}\left(x\right)dx
- u=1\text{ y }dv={\mathrm{s}\mathrm{e}\mathrm{c}}^{3}\left(x\right)dx
- u=\mathrm{s}\mathrm{e}\mathrm{c}\left(x\right)\text{ y }dv={\mathrm{s}\mathrm{e}\mathrm{c}}^{2}\left(x\right)dx
- u={\mathrm{sec}}^{2}\left(x\right)\text{ y }dv=\mathrm{sec}\left(x\right)dx
- u=\mathrm{sec}\left(x\right)\text{ y }dv=dx
Solución:
Analizando al integrando y teniendo en cuenta las fórmulas de integración y derivación, La integral de {\mathrm{sec}}^{2}\left(x\right) es inmediata, mientras que la derivada de \mathrm{sec}\left(x\right) es igual secante por tangente. Implementemos la integral para ver cómo queda.
u=\mathrm{sec}\left(x\right), dv={\mathrm{sec}}^{2}\left(x\right)dx
Derivamos e integramos.
du=\mathrm{sec}x\mathrm{tan}xdx, v=\mathrm{tan}x
\int {\mathrm{sec}}^{3}\left(x\right)dx=\mathrm{sec}\left(x\right)\mathrm{tan}x-\int \mathrm{tan}x\mathrm{sec}x\cdot \mathrm{tan}xdx
Reacomodando tenemos:
\int {\mathrm{sec}}^{3}\left(x\right)dx=\mathrm{sec}\left(x\right)\mathrm{tan}x-\int {\mathrm{tan}}^{2}x\mathrm{sec}xdx
Ahora, si aplicamos la identidad pitagórica en términos de la tangente y la secante.
\int {\mathrm{sec}}^{3}\left(x\right)dx=\mathrm{sec}\left(x\right)\mathrm{tan}x-\int \left({\mathrm{sec}}^{2}x-1\right)\mathrm{sec}xdx
\int {\mathrm{sec}}^{3}\left(x\right)dx=\mathrm{sec}\left(x\right)\mathrm{tan}x-\int {\mathrm{sec}}^{3}xdx+\int \mathrm{sec}\left(x\right)dx
Despejamos a I=\int {\mathrm{sec}}^{3}xdx .
2\int {\mathrm{sec}}^{3}\left(x\right)dx=\mathrm{sec}\left(x\right)\mathrm{tan}x+\int \mathrm{sec}\left(x\right)dx
\int {\mathrm{sec}}^{3}\left(x\right)dx=\frac{1}{2}\mathrm{sec}\left(x\right)\mathrm{tan}x+\frac{1}{2}\int \mathrm{sec}\left(x\right)dx
Esta última integral es inmediata. La respuesta correcta es el inciso b).
Llevamos la integral hasta este punto para demostrar que esta selección de variables era la correcta. En cálculo integral, muchos artificios y cambios de variable no parecen evidentes, y es precisamente esa capacidad de abstracción la que debes desarrollar resolviendo los reactivos.
Conoce la oferta académica completa del Instituto Politécnico Nacional: Lista de carreras del IPN por área.
Reactivo 23
El cambio de la variable ____ se usa para resolver la integral:
\int \frac{2{x}^{2}dx}{\sqrt{{x}^{2}-9}}
- x=3\mathrm{sec}\left(\theta \right)
- x=3\mathrm{cos}\left(\theta \right)
- x=3\mathrm{tan}\left(\theta \right)
- x=3\mathrm{csc}\left(\theta \right)
Solución:
En este caso, debemos aplicar una sustitución trigonométrica que permita resolver la integral. Recordemos rápidamente los 3 tipos de sustitución trigonométrica que existen:
Caso 1:
\sqrt{{a}^{2}-{x}^{2}}\to x=a\mathrm{sin}\theta \to dx=a\mathrm{cos}\theta d\theta
Caso 2:
\sqrt{{a}^{2}+{x}^{2}}\to x=a\mathrm{tan}\theta \to dx=a{\mathrm{sec}}^{2}\theta d\theta
Caso 3:
\sqrt{{x}^{2}-{a}^{2}}\to x=a\mathrm{sec}\theta \to dx=a\mathrm{sec}\theta \mathrm{tan}\theta d\theta
Examinando la integral del enunciado, estamos en el caso 3. La sustitución quedaría como:
\sqrt{{x}^{2}-9}=\sqrt{{x}^{2}-{3}^{2}}\to x=3\mathrm{sec}\theta
La respuesta correcta es el inciso a).
Reactivo 24
Indicar el cambio de la integral con la sustitución trigonométrica correcta.
\int \frac{dx}{\sqrt{{x}^{2}-25}}
- \int \frac{d\theta }{5\mathrm{csc}\left(\theta \right)}
- \int \mathrm{s}\mathrm{e}\mathrm{c}\left(\theta \right)d\theta
- \int \frac{d\theta }{5\mathrm{sec}\left(\theta \right)}
- \int \frac{1}{5}\mathrm{c}\mathrm{s}\mathrm{c}\left(\theta \right)d\theta
Solución:
Examinando la integral, debemos aplicar una sustitución trigonométrica. En este caso:
\sqrt{{x}^{2}-{a}^{2}}\to x=a\mathrm{sec}\theta \to dx=a\mathrm{sec}\theta \mathrm{tan}\theta d\theta
Implementado sobre nuestra integral:
\sqrt{{x}^{2}-25}=\sqrt{{x}^{2}-{5}^{2}}\to x=5\mathrm{sec}\theta \to dx=5\mathrm{sec}\theta \mathrm{tan}\theta d\theta
\int \frac{dx}{\sqrt{{x}^{2}-25}}\to \int \frac{5\mathrm{sec}\theta \mathrm{tan}\theta d\theta }{\sqrt{25{\mathrm{sec}}^{2}\theta -25}}
Simplificamos y resolvemos.
\int \frac{5\mathrm{sec}\theta \mathrm{tan}\theta d\theta }{\sqrt{25{\mathrm{sec}}^{2}\theta -25}}=\int \frac{5\mathrm{sec}\theta \mathrm{tan}\theta d\theta }{5\sqrt{{\mathrm{sec}}^{2}\theta -1}}=\int \frac{\mathrm{sec}\theta \mathrm{tan}\theta d\theta }{\sqrt{{\mathrm{tan}}^{2}\theta }}=\int \frac{\mathrm{sec}\theta \mathrm{tan}\theta d\theta }{\mathrm{tan}\theta }
\int \frac{\mathrm{sec}\theta \mathrm{tan}\theta d\theta }{\mathrm{tan}\theta }=\int \mathrm{sec}\theta d\theta
Este es el cambio que obtenemos en la integral al aplicar sustitución trigonométrica.
\int \frac{dx}{\sqrt{{x}^{2}-25}}\to \int \mathrm{sec}\theta d\theta
Llegamos hasta este punto, porque el enunciado no pide que resolvamos la integral. Comparando con los incisos, indicamos como correcto al b).
Conoce los pasos para aplicar a la universidad: Todo sobre la convocatoria del IPN.
Reactivo 25
Resolver por sustitución la integral:
\int \frac{dx}{\sqrt{4{x}^{2}+1}}
- \frac{1}{2}\mathrm{ln}\left|\sqrt{4{x}^{2}+1}-2x\right|+C
- \frac{1}{2}\mathrm{ln}\left|\sqrt{4{x}^{2}+1}+2x\right|+C
- -\frac{1}{2}\mathrm{ln}\left|\sqrt{4{x}^{2}+1}-x\right|+C
- \frac{1}{2}\mathrm{ln}\left|\sqrt{{x}^{2}+1}-2x\right|+C
Solución:
Examinando la integral y los casos de la sustitución trigonométrica, el cambio es:
\sqrt{{a}^{2}+{x}^{2}}\to x=a\mathrm{tan}\theta \to dx=a{\mathrm{sec}}^{2}\theta d\theta
Extraemos factor común el número 4.
\int \frac{dx}{\sqrt{4{x}^{2}+1}}=\int \frac{dx}{2\sqrt{{x}^{2}+\frac{1}{4}}}=\frac{1}{2}\int \frac{dx}{\sqrt{{x}^{2}+{\left(\frac{1}{2}\right)}^{2}}}
Implementado sobre nuestra integral.
\sqrt{{x}^{2}+{\left(\frac{1}{2}\right)}^{2}}\to x=\frac{1}{2}\mathrm{tan}\theta \to dx=\frac{1}{2}{\mathrm{sec}}^{2}\theta d\theta
Aplicamos la sustitución:
\int \frac{dx}{\sqrt{4{x}^{2}+1}}\to \int \frac{\frac{1}{2}{\mathrm{sec}}^{2}\theta d\theta }{\sqrt{4\left(\frac{1}{4}\right){\mathrm{tan}}^{2}\theta +1}}=\frac{1}{2}\int \frac{{\mathrm{sec}}^{2}\theta d\theta }{\sqrt{{\mathrm{tan}}^{2}\theta +1}}=\frac{1}{2}\int \frac{{\mathrm{sec}}^{2}\theta d\theta }{\sqrt{{\mathrm{sec}}^{2}\theta }}
\frac{1}{2}\int \frac{{\mathrm{sec}}^{2}\theta d\theta }{\sqrt{{\mathrm{sec}}^{2}\theta }}=\frac{1}{2}\int \frac{{\mathrm{sec}}^{2}\theta d\theta }{\mathrm{sec}\theta }=\frac{1}{2}\int \mathrm{sec}\theta d\theta
Esta última integral es inmediata.
\frac{1}{2}\int \mathrm{sec}\theta d\theta =\frac{1}{2}\mathrm{ln}\left|\mathrm{sec}\theta +\mathrm{tan}\theta \right|+C
Debemos devolver el cambio de variable. Dibujamos el triángulo:
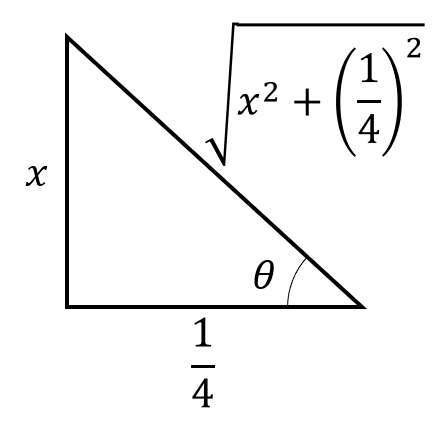
A partir del triángulo encontramos a la secante y la tangente para devolver el cambio.
\mathrm{sec}\theta =\frac{\sqrt{{x}^{2}+\frac{1}{4}}}{\frac{1}{4}}=4\sqrt{{x}^{2}+\frac{1}{4}}
\mathrm{tan}\theta =\frac{x}{\frac{1}{4}}=4x
Finalmente:
\frac{1}{2}\mathrm{ln}\left|\mathrm{sec}\theta +\mathrm{tan}\theta \right|+C\to \frac{1}{2}\mathrm{ln}\left|4\sqrt{{x}^{2}+\frac{1}{4}}+4x\right|+C
Simplificamos la raíz para asemejar nuestra solución a los incisos.
\frac{1}{2}\mathrm{ln}\left|4\sqrt{{x}^{2}+\frac{1}{4}}+4x\right|+C=\frac{1}{2}\mathrm{ln}\left|\frac{4}{2}\sqrt{4{x}^{2}+1}+4x\right|+C=\frac{1}{2}\mathrm{ln}\left|2\sqrt{4{x}^{2}+1}+4x\right|+C
\frac{1}{2}\mathrm{ln}\left|2\sqrt{4{x}^{2}+1}+4x\right|+C=\frac{1}{2}\mathrm{ln}\left|2\left(\sqrt{4{x}^{2}+1}+2x\right)\right|+C
=\frac{1}{2}\mathrm{ln}\left|\sqrt{4{x}^{2}+1}+2x\right|+\frac{1}{2}\mathrm{ln}\left|2\right|+C
Veamos que \frac{1}{2}\mathrm{ln}\left|2\right| es una constante, la cual podemos sumar con C .
\frac{1}{2}\mathrm{ln}\left|\sqrt{4{x}^{2}+1}+2x\right|+\frac{1}{2}\mathrm{ln}\left|2\right|+C=\frac{1}{2}\mathrm{ln}\left|\sqrt{4{x}^{2}+1}+2x\right|+C
\int \frac{dx}{\sqrt{4{x}^{2}+1}}=\frac{1}{2}\mathrm{ln}\left|\sqrt{4{x}^{2}+1}+2x\right|+C
Concluimos que la respuesta correcta es el inciso b).
Reactivo 26
Calcular la siguiente integral por sustitución trigonométrica.
\int \frac{dx}{x\sqrt{{x}^{2}+36}}
- \frac{1}{6}\mathrm{ln}\left|\mathit{csc}\left(\theta \right)-\mathit{tan}\left(\theta \right)\right|+c
- \frac{1}{6}\mathrm{ln}\left|\mathit{csc}\left(\theta \right)+\mathit{tan}\left(\theta \right)\right|+c
- \frac{1}{6}\mathrm{ln}\left|\mathit{sec}\left(\theta \right)-\mathit{cot}\left(\theta \right)\right|+c
- \frac{1}{6}\mathrm{ln}\left|\mathit{csc}\left(\theta \right)-\mathit{cot}\left(\theta \right)\right|+c
Solución:
Para resolver la integral, aplicamos la siguiente sustitución trigonométrica:
\sqrt{{a}^{2}+{x}^{2}}\to x=a\mathrm{tan}\theta \to dx=a{\mathrm{sec}}^{2}\theta d\theta
En nuestro caso, a=6 .
\sqrt{{6}^{2}+{x}^{2}}\to x=6\mathrm{tan}\theta \to dx=6{\mathrm{sec}}^{2}\theta d\theta
Aplicamos el cambio en la integral.
\int \frac{dx}{x\sqrt{{x}^{2}+36}}\to \int \frac{6{\mathrm{sec}}^{2}\theta d\theta }{6\mathrm{tan}\theta \sqrt{36{\mathrm{tan}}^{2}\theta +36}}
Simplificamos la integral.
\int \frac{6{\mathrm{sec}}^{2}\theta d\theta }{6\mathrm{tan}\theta \sqrt{36{\mathrm{tan}}^{2}\theta +36}}=\int \frac{{\mathrm{sec}}^{2}\theta d\theta }{\mathrm{tan}\theta \sqrt{36{\mathrm{tan}}^{2}\theta +36}}=\frac{1}{6}\int \frac{{\mathrm{sec}}^{2}\theta d\theta }{\mathrm{tan}\theta \sqrt{{\mathrm{tan}}^{2}\theta +1}}
Aplicamos la identidad pitagórica en términos de la secante y tangente en el denominador.
\frac{1}{6}\int \frac{{\mathrm{sec}}^{2}\theta d\theta }{\mathrm{tan}\theta \sqrt{{\mathrm{tan}}^{2}\theta +1}}=\frac{1}{6}\int \frac{{\mathrm{sec}}^{2}\theta d\theta }{\mathrm{tan}\theta \sqrt{{\mathrm{sec}}^{2}\theta }}=\frac{1}{6}\int \frac{{\mathrm{sec}}^{2}\theta d\theta }{\mathrm{tan}\theta \mathrm{sec}\theta }=\frac{1}{6}\int \frac{\mathrm{sec}\theta d\theta }{\mathrm{tan}\theta }
El cociente entre la secante y la tangente es igual a la cosecante.
\frac{1}{6}\int \frac{\mathrm{sec}\theta d\theta }{\mathrm{tan}\theta }=\frac{1}{6}\int \mathrm{csc}\theta d\theta
Esta integral es inmediata.
\frac{1}{6}\int \mathrm{csc}\theta d\theta =\frac{1}{6}\mathrm{ln}\left|\mathrm{csc}\theta -\mathrm{cot}\theta \right|+C
Examinando los incisos, no es necesario regresar el cambio de variable. Por lo tanto:
F\left(\theta \right)=\frac{1}{6}\mathrm{ln}\left|\mathrm{csc}\theta -\mathrm{cot}\theta \right|+C
La respuesta correcta es la opción d).
Aciertos mínimos para entrar al IPN
Reactivo 27
Indicar qué cambio de variable se requiere para resolver la siguiente integral:
\int \frac{{x}^{3}dx}{\sqrt{4{x}^{2}-4}}
- x=\mathrm{sec}\left(\theta \right)
- x=\mathrm{tan}\left(\theta \right)
- x=\mathrm{cot}\left(\theta \right)
- x=-\mathrm{csc}\left(\theta \right)
Solución:
Extraemos como factor común al número 4 del denominador.
\int \frac{{x}^{3}dx}{\sqrt{4{x}^{2}-4}}=\frac{1}{2}\int \frac{{x}^{3}dx}{\sqrt{{x}^{2}-1}}
En esta integral, aplicamos la siguiente sustitución trigonométrica.
\sqrt{{x}^{2}-1}\to x=\mathrm{sec}\theta \to dx=\mathrm{sec}\theta \mathrm{tan}\theta d\theta
Por lo tanto, el cambio de variable que permite resolver la integral es: x=\mathrm{sec}\left(\theta \right) .
Concluimos indicando como respuesta correcta al inciso a).
Reactivo 28
Calcular el denominador de la integral de acuerdo con la sustitución trigonométrica correcta.
\int \frac{dx}{\sqrt{9-{x}^{2}}}
- 3\mathrm{cos}\left(\theta \right)
- 3\mathrm{sen}\left(\theta \right)
- 3\mathrm{csc}\left(\theta \right)
- 3\mathrm{cot}\left(\theta \right)
Solución:
Analizando el denominador de la integral, la sustitución trigonométrica que permitiría resolver es:
\sqrt{9-{x}^{2}}=\sqrt{{3}^{2}-{x}^{2}}\to x=3\mathrm{sin}\theta \to dx=3\mathrm{cos}\theta d\theta
El cambio de variables es:
x=3\mathrm{sin}\theta
Aplicamos el cambio en la integral.
\int \frac{dx}{\sqrt{9-{x}^{2}}}\to \int \frac{3\mathrm{cos}\theta d\theta }{\sqrt{9-9{\mathrm{sin}}^{2}\theta }}
Simplificamos.
\int \frac{3\mathrm{cos}\theta d\theta }{\sqrt{9-9{\mathrm{sin}}^{2}\theta }}=\int \frac{3\mathrm{cos}\theta d\theta }{3\sqrt{1-1{\mathrm{sin}}^{2}\theta }}=\int \frac{3\mathrm{cos}\theta d\theta }{3\sqrt{1-1{\mathrm{sin}}^{2}\theta }}
Aplicando la identidad pitagórica.
\int \frac{3\mathrm{cos}\theta d\theta }{3\sqrt{1-1{\mathrm{sin}}^{2}\theta }}=\int \frac{3\mathrm{cos}\theta d\theta }{3\sqrt{{\mathrm{cos}}^{2}\theta }}=\int \frac{3\mathrm{cos}\theta d\theta }{3\mathrm{cos}\theta }
El denominador de la integral queda: 3\mathrm{cos}\theta .
La respuesta correcta es la opción a).
Conoce todo sobre la nueva guía de ingreso al IPN
Reactivo 29
Identificar los términos que faltan en la siguiente integral:
\int \frac{dx}{(x-2{)}^{2}(x+4)}=\int \frac{Adx}{x-2}+\int \frac{Bdx}{\_\_\_\_\_}+\int \frac{Cdx}{\_\_\_\_\_\_}
- (x-2{)}^{2}\text{ y }(x+4)
- \left(x-2\right)\text{ y }\left(x+4\right)
- (x-2)\text{ y }(x+4{)}^{2}
- (x-2{)}^{2}\text{ y }(x+4{)}^{2}
Solución:
En la descomposición de fracciones parciales, cuando hay factores lineales repetidos (o expresados como una potencia), la descomposición de esos factores lineales se realiza incrementando la potencia hasta llegar a la potencia total.
Para la integral del enunciado, el factor lineal es x-2 y se encuentra repetido dos veces. Por lo tanto, la descomposición quedaría:
\int \frac{dx}{(x-2{)}^{2}(x+4)}=\int \frac{Adx}{x-2}+\int \frac{Bdx}{{\left(x-2\right)}^{2}}+\int \frac{Cdx}{x+4}
Los factores lineales faltantes son: (x-2{)}^{2}\text{ y }(x+4) .
La respuesta correcta es el inciso a).
Reactivo 30
Señalar la integral que es equivalente a:
\int \frac{5}{(x+3{)}^{2}(x-2)}dx
- \int \frac{C}{x-2}dx+\int \frac{B}{(x-2{)}^{2}}dx+\int \frac{A}{x+3}dx
- \int \frac{C}{x-2}dx+\int \frac{Bx}{(x-2{)}^{2}}dx+\int \frac{A}{x+3}dx
- \int \frac{C}{x-2}dx+\int \frac{B}{(x+3{)}^{2}}dx+\int \frac{A}{x+3}dx
- \int \frac{C}{x-2}dx+\int \frac{B}{(x+3{)}^{2}}dx+\int \frac{Ax}{x+3}dx
Solución:
Para resolver esta integral, hay que aplicar fracciones parciales al integrando. Tenemos un factor lineal repetido 2 veces (de potencia 2). La descomposición en factores parciales debe ser:
\int \frac{5}{(x+3{)}^{2}(x-2)}dx=\int \frac{A}{x+3}dx+\int \frac{B}{(x+3{)}^{2}}dx+\int \frac{C}{x-2}dx
La respuesta correcta es el inciso c).


