¡Hola aspirante! En este tutorial vamos a resolver los 40 ejercicios de cálculo diferencial de la guía de estudio IPN como preparación para tu examen de ingreso a la universidad.

Por motivos didácticos hemos dividido la guía de cálculo diferencial en cuatro partes. En esta ocasión vamos a resolver la primera parte de los reactivos de cálculo integral, desde el reactivo 1 hasta el 10.
El siguiente es un resumen de la convocatoria IPN.
- Carreras ofertadas en IPN: 70+.
- Porcentaje de Aceptación: 20%.
- Preguntas en el examen de Admisión: 140 preguntas.
- Nuevos temas: historia e inglés (reading comprehension).
- Tipo: selección múltiple.
Estructura del Examen IPN
La estructura del examen al IPN 2023 ha sido modificada. Ahora, el número de reactivos cambia según el área de conocimientos. Las carreras en el Instituto Politécnico Nacional se dividen en 3 áreas:
- Ingeniería y Ciencias Físico Matemáticas IyCFM
- Ciencias Sociales y Administrativas CSA
- Ciencias Médico Biológicas CMB
La siguiente tabla muestra la estructura de reactivos por materia para cada área.
| Materia | IyCFM | CMB | CSyA |
|---|---|---|---|
| Matemáticas | 37 | 33 | 35 |
| Competencia escrita | 20 | 20 | 25 |
| Competencia lectora | 20 | 20 | 20 |
| Reading comprehension | 10 | 10 | 10 |
| Historia | 10 | 10 | 20 |
| Biología | 9 | 17 | 10 |
| Química | 17 | 17 | 10 |
| Física | 17 | 13 | 10 |
¿Qué tan difícil es el examen al IPN?
La respuesta es muy sencilla, ya que depende de un único factor: tu nivel de preparación antes del examen.
Conoce todo sobre el proceso de ingreso a la universidad en la convocatoria del IPN.
En esta convocatoria se incluyen 2 nuevas asignaturas, aumentando la cantidad de reactivos a 140. En la guía de cálculo diferencial se incluyen reactivos que cubren los temas de la asignatura con un nivel de complejidad variado.
Temario cálculo diferencial IPN 2023
Estos son los temas de cálculo diferencial que deberás estudiar antes de presentar el examen:
- Cálculo diferencial
- Funciones, límites y continuidad
- Dominio y rango
- Desigualdades
- Definición de límite
- Teorema de límites
- Límites al infinito
- Continuidad de una función
- Derivada de funciones algebraicas y trascendentes
- Definición de derivada
- Interpretación geométrica
- Fórmulas de derivadas
- Regla de la cadena
- Máximos y mínimos
- Funciones, límites y continuidad
¿Cómo resolver la guía del IPN 2023?
Te aconsejo examinar la bibliografía recomendada en la guía del IPN antes de pasar con los reactivos. De esta manera tendrás una idea general de algunos conceptos básicos. No inicies la resolución de los reactivos sin tener el conocimiento previo de la asignación, estudiar de esta forma es poco efectivo para el proceso de aprendizaje.
Los siguientes hacks te ayudarán a mejorar tu desempeño, resolviendo la mayor cantidad de reactivos en el menor tiempo para obtener los aciertos que necesitas para ser admitido.
- Resuelve cada parte por tu cuenta antes de checar las respuestas. Utiliza este material a modo de consulta.
- Establece un tiempo no mayor a 15 minutos por cada 10 reactivos.
- Analiza el procedimiento al resolver los ejercicios y piensa en posibles alternativas que mejoren tu tiempo.
- Si un ejercicio parece complejo, ve al siguiente y resuélvelo de último. Lo mejor es mantener la concentración y no entrar en pánico.
- Te advierto que la guía del IPN 2023 tiene algunos errores, aquí te señalamos cuáles son.
- Cálculo diferencial tiene un temario amplio. Asegúrate de entender los conceptos, teoremas y demostraciones antes pasar con los reactivos.
Reactivo 1
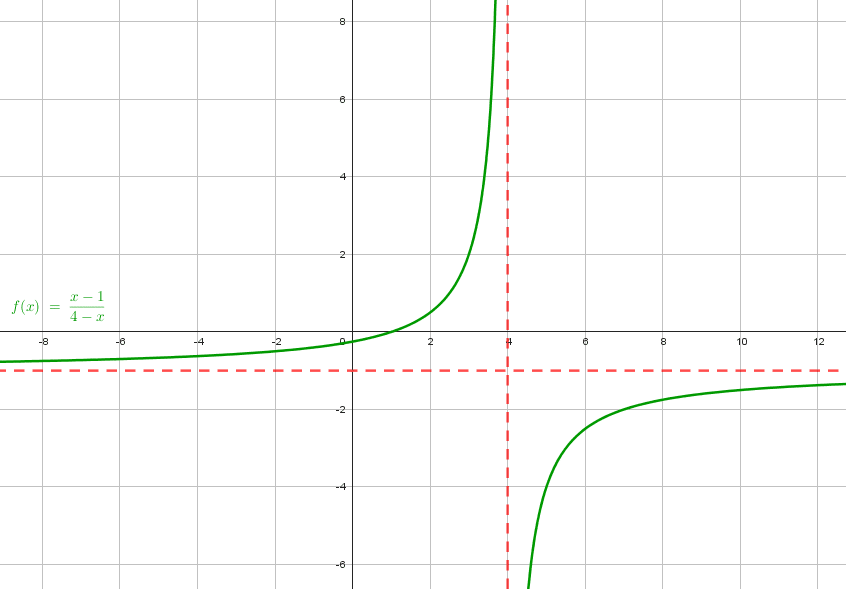
Determinar el dominio y rango de la función f\left(x\right)=\frac{x-1}{4-x} .
- \left(-\mathrm{\infty },1\right)\cup \left(4,\mathrm{\infty }\right) (-\mathrm{\infty },-1)\cup (-1,\mathrm{\infty })
- \left(-\mathrm{\infty },1\right]\cup \left[4,\mathrm{\infty }\right) (-\mathrm{\infty },-1)\cup [-1,\mathrm{\infty })
- \left(-\mathrm{\infty },4\right)\cup \left(4,\mathrm{\infty }\right) (-\mathrm{\infty },-1)\cup (-1,\mathrm{\infty })
- \left(-\mathrm{\infty },-4\right)\cup \left(4,\mathrm{\infty }\right) (-\mathrm{\infty },-1)\cup [-1,\mathrm{\infty })
Solución:
Iniciamos calculando el dominio de la función. Recordemos que el dominio se calcula a partir de las restricciones que presentan las funciones básicas. Debido a que la función del enunciado es racional, la restricción es que el denominador sea diferente de cero.
\mathrm{D}\mathrm{o}\mathrm{m}\left(f\right)=x | x\in 4-x\ne 0
Resolvemos la desigualdad.
4-x\ne 0\to -x\ne -4
\therefore x\ne 4
Es decir, cualquier valor de x diferente a 4. Esto se expresa mediante notación de intervalos como:
\mathrm{D}\mathrm{o}\mathrm{m}\left(f\right)=x | x\in \left(-\infty , 4\right)\cup \left(4, \infty \right)
El único inciso que muestra este resultado para el dominio es el c). Por tanto, concluimos que la respuesta correcta es el inciso c).
Reactivo 2
Identificar el dominio de la función:
f\left(x\right)=\frac{3{x}^{2}}{{x}^{2}-1}
- \left\{x\in \mathbb{R}:x\ne 1\right\}
- \left\{x\in \mathbb{R}:x\ne 1,x\ne 0\right\}
- \left\{x\in \mathbb{R}:x\ne 1,x\ne -1\right\}
- \left\{x\in \mathbb{R}:x\ne 1,x\ne -1,x\ne 0\right\}
Solución:
La función es racional y la única restricción que posee es que el denominador sea diferente de cero.
{x}^{2}-1\ne 0
Despejamos la x , recordando que al simplificar una potencia al cuadrado se debe colocar \pm .
{x}^{2}-1\ne 0\to {x}^{2}\ne 1\to x\ne \pm \sqrt{1}
\therefore x\ne \pm 1
El dominio de f\left(x\right) es cualquier valor de x excepto 1 y -1 . El enunciado que expresa esto en notación de conjunto es el c).
Reactivo 3
Determinar el dominio de la función
f\left(x\right)=\sqrt{\frac{x-1}{x-4}}
- \left(-\mathrm{\infty },1\right)\cup \left(4,\mathrm{\infty }\right)
- \left(-\mathrm{\infty },1\right]\cup \left[4,\mathrm{\infty }\right)
- \left(-\mathrm{\infty },1\right]\cup \left(4,\mathrm{\infty }\right)
- \left[-\mathrm{\infty },1\right]\cup \left[4,\mathrm{\infty }\right]
Solución:
Este problema se puede resolver solo con análisis y sin realizar ningún cálculo. Iniciemos identificando que el interior de la raíz cuadrada tiene una función racional, cuya condición de existencia es que el denominador sea distinto de cero.
El denominador se hace cero cuando x=4 , por lo tanto, nos quedamos con los incisos que muestran al 4 en un intervalo abierto (es decir, con paréntesis). Dichos incisos son el a y el c. Examinemos ahora \left(-\mathrm{\infty },1\right) y \left(-\mathrm{\infty },1\right] en los incisos seleccionados.
El radicando de una raíz cuadrada puede valer cero o un número mayor que cero. El valor de x en el que se anula la fracción \frac{x-1}{x-4} es x=1 .
Por lo tanto, este valor se puede incluir en el primer intervalo de la solución. El inciso a) excluye al 1 \left(-\infty , 1\right) , concluimos entonces que la respuesta correcta es el inciso c).
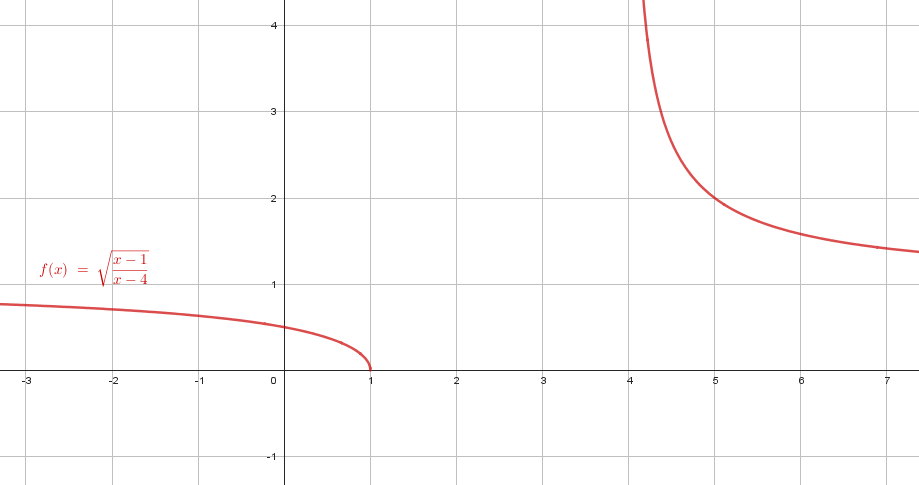
Es conveniente hacer este análisis en el examen, de lo contrario, deberás aplicar un estudio de signos sobre la inecuación \frac{x-1}{x-4}\ge 0 .
Reactivo 4
Identificar el dominio y rango de la función que se muestra en la gráfica:
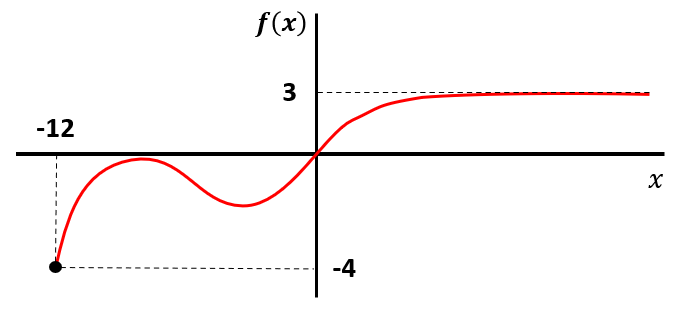
- {D}_{f}=\left[-12,\mathrm{\infty }\right),{R}_{f}=\left(-\mathrm{4,3}\right)
- {D}_{f}=\left[-12,\mathrm{\infty }\right),{R}_{f}=\left[-\mathrm{4,3}\right)
- {D}_{f}=\left(-12,\mathrm{\infty }\right),{R}_{f}=\left[-\mathrm{4,3}\right)
- {D}_{f}=\left[-12,\mathrm{\infty }\right],{R}_{f}=\left(-\mathrm{4,3}\right)
Solución:
El dominio de una función, es el conjunto formado por todos los valores de x en los que se encuentra definida dicha función. Por otro lado, el rango es el conjunto de valores con todas las imágenes en y que toma la función al ser evaluada en su dominio.
Lo anterior quiere decir: el dominio son todos los valores posibles de x y el rango todos los valores posibles de y . Examinando la imagen, la función se encuentra definida en x desde -12 hasta +\infty .
\mathrm{D}\mathrm{o}\mathrm{m}\left(f\right)=\left[-12, \infty \right)
El -12 se incluye, porque el punto se encuentra relleno.
El rango de la función va desde el -4 incluido (porque el punto está relleno) hasta el 3 excluido porque la función nunca llega al 3, se acerca a él asintóticamente.
\mathrm{R}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{o}\left(f\right)=\left[-4, 3\right)
Finalmente:
\mathrm{D}\mathrm{o}\mathrm{m}\left(f\right)=\left[-12, \infty \right), \mathrm{R}\mathrm{a}\mathrm{n}\mathrm{g}\mathrm{o}\left(f\right)=\left[-4, 3\right)
La respuesta correcta es el inciso b).
Reactivo 5
Resolver la siguiente desigualdad:
\frac{x+1}{x-1}<1
- \left(-\mathrm{\infty },1\right)
- \left(-\mathrm{\infty },0\right)
- \left(-\mathrm{\infty },1\right]
- \left(-\mathrm{\infty },0\right]
Solución:
Iniciamos pasando el 1 a restar al miembro de la izquierda.
\frac{x+1}{x-1}<1\to \frac{x+1}{x-1}-1<0
Simplificamos.
\frac{x+1-x+1}{x-1}<0\to \frac{2}{x-1}<0
Para que una fracción de como resultado un número negativo (menor que cero), el numerador y el denominador deben tener signos distintos. Como el numerador es +2, para que el resultado sea negativo el denominador debe ser menor que cero.
x-1<0\to x<1
Expresado en notación de intervalo:
x\in \left(-\infty , 1\right)
Concluimos indicando como respuesta correcta al inciso a).
Reactivo 6
Identificar el intervalo de solución para la siguiente desigualdad:
\left|\frac{3x-2}{2x-5/4}\right|<1
- \left(\frac{13}{20},\frac{3}{4}\right)
- \left(\frac{3}{4},\frac{18}{20}\right)
- \left(-\frac{13}{20},\frac{3}{4}\right)
- \left(-\frac{3}{4},\frac{18}{20}\right)
Solución:
Descomponemos a la desigualdad del valor absoluto como una inecuación doble.
\left|\frac{3x-2}{2x-5/4}\right|<1\to -1<\frac{3x-2}{2x-\frac{5}{4}}<1
Esto nos deja dos inecuaciones para resolver:
{i}_{1}:-1<\frac{3x-2}{2x-\frac{5}{4}}\to \frac{3x-2}{2x-\frac{5}{4}}>-1
{i}_{2}: \frac{3x-2}{2x-\frac{5}{4}}<1
Debemos resolver ambas inecuaciones. La solución total será la unión de las soluciones parciales {i}_{1} e {i}_{2} .
Solución de la primera inecuación.
\frac{3x-2}{2x-\frac{5}{4}}>-1\to \frac{3x-2}{2x-\frac{5}{4}}+1>0\to \frac{3x-2+2x-\frac{5}{4}}{2x-\frac{5}{4}}>0
\frac{5x-\frac{13}{4}}{2x-\frac{5}{4}}>0\to \frac{20x-13}{8x-5}>0
Esta desigualdad se cumplirá siempre que:
{i}_{11}:\begin{array}{c}20x-13>0\\ 8x-5>0\end{array} \mathrm{ó}\mathrm{ }{i}_{12}:\mathrm{ }\begin{array}{c}20x-13<0\\ 8x-5<0\end{array}
Resolvemos a {i}_{11} .
\begin{array}{c}20x-13>0\\ 8x-5>0\end{array}\to \begin{array}{c}20x>13\\ 8x>5\end{array}\to \begin{array}{c}x>\frac{13}{20}\\ x>\frac{5}{8}\end{array}
Intersecamos ambas desigualdades.
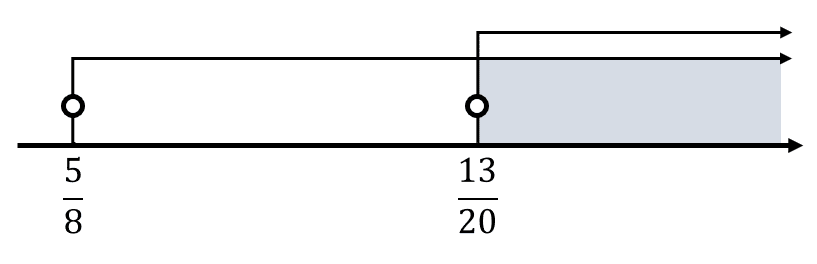
Solución {i}_{11} :
x\in \left(\frac{13}{20}, \infty \right)
Resolvemos a {i}_{12} .
\begin{array}{c}20x-13<0\\ 8x-5<0\end{array}\to \begin{array}{c}20x<13\\ 8x<5\end{array}\to \begin{array}{c}x<\frac{13}{20}\\ x<\frac{5}{8}\end{array}
Intersecamos las desigualdades.

Solución {i}_{12} :
x\in \left(-\infty , \frac{5}{8}\right)
Solución de la inecuación {i}_{1} :
{i}_{1}={i}_{11}\cup {i}_{12}=\left(-\infty , \frac{5}{8}\right)\cup \left(\frac{13}{20}, \infty \right)
{i}_{1}=x\in \left(-\infty , \frac{5}{8}\right)\cup \left(\frac{13}{20}, \infty \right)
Solución de la segunda inecuación.
\frac{3x-2}{2x-\frac{5}{4}}<1\to \frac{3x-2}{2x-\frac{5}{4}}-1<0\to \frac{3x-2-2x+\frac{5}{4}}{2x-\frac{5}{4}}<0
\frac{x-\frac{3}{4}}{2x-\frac{5}{4}}<0\to \frac{4x-3}{8x-5}<0
Esta desigualdad se cumplirá siempre que:
{i}_{21}: \begin{array}{c}4x-3<0\\ 8x-5>0\end{array} \mathrm{ó}\mathrm{ }{i}_{22}:\begin{array}{c}4x-3>0\\ 8x-5<0\end{array}
Resolvemos a {i}_{21} .
\begin{array}{c}4x-3<0\\ 8x-5>0\end{array}\to \begin{array}{c}4x<3\\ 8x>5\end{array}\to \begin{array}{c}x<\frac{3}{4}\\ x>\frac{5}{8}\end{array}
Intersecando:

Solución {i}_{21} :
x\in \left(\frac{5}{8},\frac{3}{4}\right)
Resolvemos a {i}_{22} .
\begin{array}{c}4x-3>0\\ 8x-5<0\end{array}\to \begin{array}{c}4x>3\\ 8x<5\end{array}\to \begin{array}{c}x>\frac{3}{4}\\ x<\frac{5}{8}\end{array}
\mathrm{S}\mathrm{o}\mathrm{l}\mathrm{u}\mathrm{c}\mathrm{i}\mathrm{ó}\mathrm{n}\mathrm{ }{i}_{22}:
x\in \left\{\varnothing \right\}
Solución de la inecuación {i}_{2} :
{i}_{2}={i}_{21}\cup {i}_{22}=\left(\frac{5}{8},\frac{3}{4}\right)\cup \left\{\varnothing \right\}=\left(\frac{5}{8},\frac{3}{4}\right)
{i}_{2}=x\in \left(\frac{5}{8},\frac{3}{4}\right)
Solución total de la inecuación original:
i={i}_{1}\cap {i}_{2}=\left[\left(-\infty , \frac{5}{8}\right)\cup \left(\frac{13}{20}, \infty \right)\right]\cap \left(\frac{5}{8},\frac{3}{4}\right)
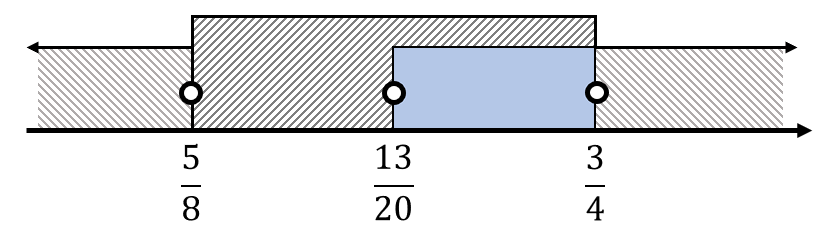
i=x\in \left(\frac{13}{20},\frac{3}{4}\right)
La respuesta correcta es el inciso a).
Reactivo 7
Identificar el intervalo de valores para x de la desigualdad \frac{1}{5}-\frac{1}{3}(x-1)\le \frac{x}{3}-1 .
- x\in \left(-\mathrm{\infty },\frac{23}{10}\right]
- x\in \mathbb{R}-\frac{23}{10}
- x\in \left[\frac{23}{10},\mathrm{\infty }\right)
- x\in \left(-\mathrm{\infty },\frac{23}{10}\right)
Solución:
Iniciamos desarrollando el producto notable.
\frac{1}{5}-\frac{1}{3}\left(x-1\right)\le \frac{x}{3}-1\to \frac{1}{5}-\frac{x}{3}+\frac{1}{3}\le \frac{x}{3}-1
Agrupamos y simplificamos.
\frac{1}{5}--\frac{x}{3}+\frac{1}{3}\le \frac{x}{3}-1\to -\frac{x}{3}-\frac{x}{3}\le -\frac{1}{3}-\frac{1}{5}-1
-\frac{2x}{3}\le -\frac{1}{3}-\frac{1}{5}-1
-\frac{2x}{3}\le -\frac{23}{15}
Multiplicamos por -1 y cambiamos la dirección de la desigualdad.
-\frac{2x}{3}\le -\frac{23}{15}\to \frac{2x}{3}\ge \frac{23}{15}
x\ge \frac{23}{10}
Expresado en notación de intervalo:
x\in \left[\frac{23}{10}, \infty \right)
Indicamos como respuesta correcta al inciso c).
Reactivo 8
Resolver la siguiente desigualdad:
{x}^{2}-4\ge 0
- \left(-\mathrm{\infty },4\right)\cup \left(4,\mathrm{\infty }\right)
- \left(-\mathrm{\infty },4\right]\cup \left[4,\mathrm{\infty }\right)
- \left(-\mathrm{\infty },2\right)\cup \left(2,\mathrm{\infty }\right)
- \left(-\mathrm{\infty },-2\right]\cup \left[2,\mathrm{\infty }\right)
Solución:
Factorizamos el binomio.
\left(x-2\right)\left(x+2\right)\ge 0
Dicho producto será positivo cuando los factores sean positivos o negativos, simultáneamente.
{i}_{1}:\begin{array}{c}x-2\ge 0\\ x+2\ge 0\end{array}
{i}_{2}:\begin{array}{c}x-2\le 0\\ x+2\le 0\end{array}
Resolvemos el primer sistema de inecuaciones.
\begin{array}{c}x-2\ge 0\\ x+2\ge 0\end{array}\to \begin{array}{c}x\ge 2\\ x\ge -2\end{array}
Intersecando:
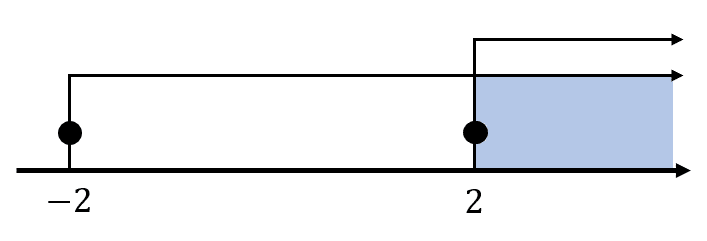
{i}_{1}=\left[2, \infty \right)
No es necesario continuar resolviendo, porque el único inciso que posee entre sus intervalos \left[2, \infty \right) es el inciso d).
Reactivo 9
Para que exista el límite de una función donde \text{c }y L son números reales y x tiende hacia c, se debe cumplir que:
- \underset{x\to {c}^{-}}{lim} f\left(x\right)=L\text{ y }\underset{x\to {c}^{+}}{lim} f\left(x\right)=L
- \underset{x\to {c}^{-}}{lim} f\left(x\right)=f\left(c\right)\text{ y }\underset{x\to {c}^{+}}{lim} f\left(x\right)=L
- \underset{x\to {c}^{-}}{lim} f\left(x\right)=L\text{ y }\underset{x\to {c}^{+}}{lim} f\left(x\right)=f\left(L\right)
- \underset{x\to {c}^{-}}{lim} f\left(x\right)=f\left(c\right)\text{ y }\underset{x\to {c}^{+}}{lim} f\left(x\right)=L
Solución:
El límite de una función real f\left(x\right) existe cuando x\to c , si los límites laterales \underset{x\to {c}^{-}}{lim} f\left(x\right) y \underset{x\to {c}^{+}}{lim} f\left(x\right) existen y tienen el mismo valor L . Seleccionamos como respuesta correcta al inciso a).
Reactivo 10
Identificar el intervalo de solución
2{x}^{3}-7{x}^{2}-17x\le -10
- \left(-\mathrm{\infty },-\frac{1}{2}\right]\cup \left(\mathrm{2,5}\right)
- \left(-\mathrm{\infty },-2\right]\cup \left[\frac{1}{2},5\right]
- \left(-\mathrm{\infty },\frac{1}{2}\right]\cup \left(\mathrm{2,5}\right)
- \left(-\mathrm{\infty },-\frac{1}{2}\right]\cup \left[\frac{1}{2},5\right]
Solución:
Iniciamos pasando el -10 a sumar al primer miembro.
2{x}^{3}-7{x}^{2}-17x\le -10\to 2{x}^{3}-7{x}^{2}-17x+10\le 0
Debido a que el polinomio es de tercer grado, debemos factorizar para poder resolver la desigualdad. Aplicamos la regla de Ruffini para calcular los factores del polinomio.
Regla de Ruffini.
Escribimos los coeficientes del polinomio.

Bajamos el 2 y buscamos un número que nos permita eliminar al 10.
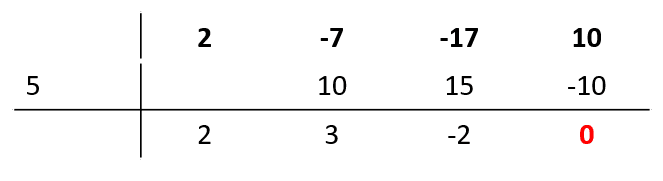
Buscamos un número que nos permita eliminar al -2.
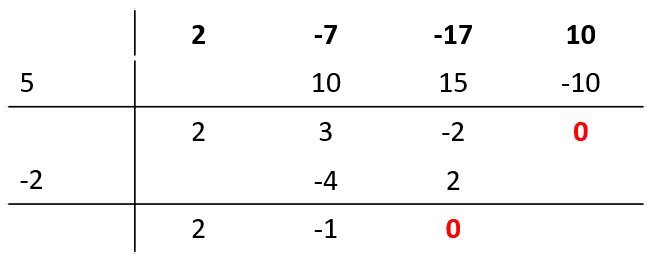
Escribimos la expresión factorizada, recordando que el 5 y el -2 se escriben con el signo cambiado.
2{x}^{3}-7{x}^{2}-17x+10=\left(x-5\right)\left(x+2\right)\left(2x-1\right)
La inecuación quedaría como:
\left(x-5\right)\left(x+2\right)\left(2x-1\right)\le 0
Despejamos los valores de x que anulan a cada factor.
x-5=0\to x=5
x+2=0\to x=-2
2x-1=0\to x=\frac{1}{2}
Situamos todos sobre una recta real para realizar el estudio de signos de los 3 factores.
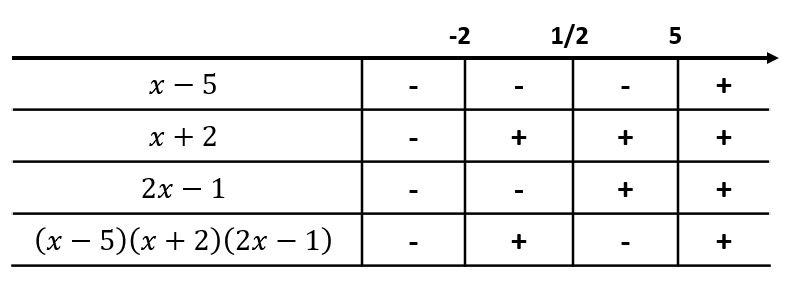
El polinomio de tercer grado es menor o igual que cero en los intervalos \left(-\infty , -2\right] y \left[\frac{1}{2}, 5\right] . Finalmente:
x\in \left(-\infty , -2\right]\cup \left[\frac{1}{2}, 5\right]
La respuesta correcta es el inciso b).


