Guía IPN 2023 Cálculo Diferencial Parte 2 del 11 al 20

Continuamos con la solución de la guía de estudios de cálculo diferencial para el examen de ingreso al IPN 2023. En esta segunda parte vamos a resolver los ejercicios del 11 al 20.

Regresar a la parte 1

Desarrolla los reactivos por tu cuenta antes de revisar la solución. Cálculo es una asignatura desafiante, analiza los problemas y toma tiempo necesario para encontrar la respuesta correcta.

Reactivo 11

Calcular el límite \underset{x\to c}{lim} \left[f\right(x)\cdot g(x\left)\right] , si \underset{x\to c}{lim} f\left(x\right)={2}^{n}\text{ y }\underset{x\to c}{lim} g\left(x\right)={3}^{n+1} .

1. 3\left({6}^{n}\right)
2. 3\left({6}^{n+1}\right)
3. (36{)}^{n}
4. (36{)}^{n+1}

Solución:

Para el cálculo de este límite, debemos utilizar la propiedad del límite de un producto.

\underset{x\to a}{\mathrm{lim}}\left[f\left(x\right)\cdot g\left(x\right)\right]=\underset{x\to a}{\mathrm{lim}}f\left(x\right)\cdot \underset{x\to a}{\mathrm{lim}}g\left(x\right)

Ya que el enunciado nos indica el valor de los límites para f\left(x\right) y g\left(x\right) , solo nos queda sustituir en el límite general para obtener el resultado final.

\mathrm{ }\underset{x\to c}{lim} \left[f\left(x\right)\cdot g\left(x\right)\right]=\underset{x\to c}{\mathrm{lim}}f\left(x\right)\cdot \underset{x\to c}{\mathrm{lim}}g\left(x\right)=\left({2}^{n}\right)\left({3}^{n+1}\right)

Simplificamos el producto de potencias.

\underset{x\to c}{lim} \left[f\left(x\right)\cdot g\left(x\right)\right]=3\left({2}^{n}\right)\left({3}^{n}\right)=3\left({6}^{n}\right)

Finalizamos la solución indicando como respuesta correcta al inciso a).

Reactivo 12

Calcular el límite de la función

\underset{x\to 9}{lim} \frac{x-9}{\sqrt{x}-3}

1. 3
2. 4
3. 6
4. 8

Solución:

Iniciamos evaluando el límite para identificar el tipo de indeterminación que se presenta.

\underset{x\to 9}{lim} \frac{x-9}{\sqrt{x}-3}=\frac{9-9}{\sqrt{9}-3}=\frac{0}{0}

Es una indeterminación 0/0 . Debemos aplicar transformaciones algebraicas para eliminar la indeterminación. Podemos aplicar diferencia de cuadrados en el numerador.

x-9={\left(\sqrt{x}\right)}^{2}-{3}^{2}=\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)

Sustituimos en el límite.

\underset{x\to 9}{lim} \frac{x-9}{\sqrt{x}-3}=\underset{x\to 9}{lim} \frac{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}{\sqrt{x}-3}=\underset{x\to 9}{lim} \left(\sqrt{x}+3\right)

Evaluamos nuevamente.

\underset{x\to 9}{lim} \left(\sqrt{x}+3\right)=\sqrt{9}+3=3+3=6

Finalmente:

\underset{x\to 9}{lim} \frac{x-9}{\sqrt{x}-3}=6

Concluimos indicando como respuesta correcta al inciso c).

Reactivo 13

Identificar el paso incorrecto en la prueba de continuidad de la función f\left(x\right)=(x-4{)}^{3}\text{, en }x=4

Pasos:

1. f\left(4\right)=(4-4{)}^{3}=0
2. \underset{x\to 4}{lim} (x-4{)}^{3}=0
3. \underset{x\to 4}{lim} (x-4{)}^{3}=f(0)
4. \underset{x\to {4}^{-}}{lim} (x-4{)}^{3}=\underset{x\to {4}^{+}}{lim} (x-4{)}^{3}

1. 1
2. 2
3. 3
4. 4

Solución:

Para que una función sea continua en un punto x=a , se deben cumplir las siguientes condiciones:

1. La función f\left(x\right) debe estar definida en el punto: a\in \mathrm{D}\mathrm{o}\mathrm{m}\left(f\right) .
2. El límite de f\left(x\right) cuando x\to a
3. El límite de la función en el punto y la función evaluada en x=a , deben ser iguales.

En el primer inciso se evalúa a la función en el punto, procedimiento que se realiza correctamente. En el segundo inciso se calcula el límite de f\left(x\right) cuando x\to 4 .

En el tercer paso se intenta plasmar la igualdad entre el límite y la función evaluada en el punto, pero el punto indicado en la función es x=0 y no x=4 . Por lo tanto, este es el paso incorrecto. La respuesta correcta es el inciso c).

Reactivo 14

Calcular el límite de la función \underset{x\to -2}{lim} \frac{{x}^{3}+8}{x+2} .

1. 12
2. 8
3. 4
4. 2

Solución:

Iniciamos evaluando el límite en el punto.

\underset{x\to -2}{lim} \frac{{x}^{3}+8}{x+2}=\frac{{\left(-2\right)}^{3}+8}{-2+2}=\frac{0}{0}

Hay una indeterminación 0/0 . Para romper la indeterminación, debemos factorizar la suma de cubos en el numerador.

{x}^{3}+8={x}^{3}+{2}^{3}

La fórmula de factorización es:

{a}^{3}+{b}^{3}=\left(a+b\right)\left({a}^{2}-ab+{b}^{2}\right)

Aplicando la fórmula al problema nos queda:

{x}^{3}+{2}^{3}=\left(x+2\right)\left({x}^{2}-2x+4\right)

Sustituimos en el límite.

\underset{x\to -2}{lim} \frac{{x}^{3}+8}{x+2}=\underset{x\to -2}{lim} \frac{\left(x+2\right)\left({x}^{2}-2x+4\right)}{x+2}=\underset{x\to -2}{lim} \left({x}^{2}-2x+4\right)

Evaluamos al límite para comprobar que se ha roto la indeterminación.

\underset{x\to -2}{lim} \left({x}^{2}-2x+4\right)={\left(-2\right)}^{2}-2\left(-2\right)+4=4+4+4=12

Finalmente:

\underset{x\to -2}{lim} \frac{{x}^{3}+8}{x+2}=12

La respuesta correcta es el inciso a).

Conoce la oferta académica completa del Instituto Politécnico Nacional: Lista de carreras del IPN por área.

Reactivo 15

Determinar el valor del límite {\left[\underset{x\to a}{lim} f\left(x\right)\right]}^{6} dado que \underset{x\to a}{lim} f\left(x\right)=\sqrt{3}

1. 3
2. 9
3. 27
4. 81

Solución:

En este caso, nos apoyamos en la propiedad del límite de una potencia.

\underset{x\to a}{\mathrm{lim}}f{\left(x\right)}^{n}={\left[\underset{x\to a}{\mathrm{lim}}f\left(x\right)\right]}^{n}

El enunciado ya nos indica el límite con la propiedad aplicada. Esta comprobación es un recordatorio de la propiedad y de que ha sido aplicada en el problema.

Tenemos el valor del límite, procedemos a sustituirlo.

{\left[\underset{x\to a}{lim} f\left(x\right)\right]}^{6}={\left[\sqrt{3}\right]}^{6}={3}^{3}=27

Finalmente:

{\left[\underset{x\to a}{lim} f\left(x\right)\right]}^{6}=27

Indicamos como respuesta correcta a la opción c).

Reactivo 16

Calcular el límite \underset{x\to \pi /4}{lim} \frac{\mathrm{s}\mathrm{e}\mathrm{n}\left(x\right)\cdot \mathrm{c}\mathrm{o}\mathrm{s}\left(x\right)}{x}

1. \frac{\pi }{2}
2. \frac{\pi }{4}
3. \frac{4}{\pi }
4. \frac{2}{\pi }

Solución:

Iniciamos evaluando el límite en el punto.

\underset{x\to \pi /4}{lim} \frac{\mathrm{s}\mathrm{e}\mathrm{n}\left(x\right)\cdot \mathrm{c}\mathrm{o}\mathrm{s}\left(x\right)}{x}=\frac{\mathrm{sen}\left(\frac{\pi }{4}\right)\cdot \mathrm{cos}\left(\frac{\pi }{4}\right)}{\frac{\pi }{4}}

\frac{\mathrm{sen}\left(\frac{\pi }{4}\right)\cdot \mathrm{cos}\left(\frac{\pi }{4}\right)}{\frac{\pi }{4}}=\frac{4}{\pi }\left(\frac{\sqrt{2}}{2}\right)\left(\frac{\sqrt{2}}{2}\right)=\frac{4}{\pi }\cdot \frac{2}{4}=\frac{2}{\pi }

Finalmente:

\underset{x\to \pi /4}{lim} \frac{\mathrm{s}\mathrm{e}\mathrm{n}\left(x\right)\cdot \mathrm{c}\mathrm{o}\mathrm{s}\left(x\right)}{x}=\frac{2}{\pi }

Indicamos al inciso d) como la respuesta correcta.

Conoce los pasos para aplicar a la universidad: Todo sobre la convocatoria del IPN.

Reactivo 17

Si k\text{ y r } son diferentes de cero, determinar el siguiente límite:

\underset{x\to \mathrm{\infty }}{lim} \frac{{k}^{2}{x}^{2}-{r}^{2}x+7a}{k{x}^{2}-rx+4b}

1. k
2. {k}^{2}
3. r
4. {r}^{2}

Solución:

Debido a que es un límite al infinito, debemos dividir tanto al numerador como al denominador por la mayor potencia de x . En este caso, la mayor potencia es {x}^{2} .

\underset{x\to \mathrm{\infty }}{lim} \frac{{k}^{2}{x}^{2}-{r}^{2}x+7a}{k{x}^{2}-rx+4b}=\underset{x\to \mathrm{\infty }}{lim} \frac{\frac{{k}^{2}{x}^{2}}{{x}^{2}}-\frac{{r}^{2}x}{{x}^{2}}+\frac{7a}{{x}^{2}}}{\frac{k{x}^{2}}{{x}^{2}}-\frac{rx}{{x}^{2}}+\frac{4b}{{x}^{2}}}=\underset{x\to \mathrm{\infty }}{lim} \frac{{k}^{2}-\frac{{r}^{2}}{x}+\frac{7a}{{x}^{2}}}{k-\frac{r}{x}+\frac{4b}{{x}^{2}}}

Evaluamos el límite.

\underset{x\to \mathrm{\infty }}{lim} \frac{{k}^{2}-\frac{{r}^{2}}{x}+\frac{7a}{{x}^{2}}}{k-\frac{r}{x}+\frac{4b}{{x}^{2}}}=\frac{{k}^{2}-0+0}{k-0+0}=\frac{{k}^{2}}{k}=k

Finalmente:

\underset{x\to \mathrm{\infty }}{lim} \frac{{k}^{2}{x}^{2}-{r}^{2}x+7a}{k{x}^{2}-rx+4b}=k

Concluimos indicando como respuesta correcta al inciso a).

Reactivo 18

Calcular el límite de la siguiente función:

\underset{x\to \mathrm{\infty }}{lim} \frac{6{x}^{5}-3{x}^{3}+{x}^{2}}{\left({x}^{2}-3\right)\left(2{x}^{3}+x-8\right)}

1. -\frac{3}{11}
2. \frac{18}{2}
3. -2
4. 3

Solución:

Este límite al infinito presenta una indeterminación \infty /\infty  . Debemos dividir por la mayor potencia de x . Revisando a la función, la mayor potencia es {x}^{5} .

\underset{x\to \mathrm{\infty }}{lim} \frac{\frac{6{x}^{5}}{{x}^{5}}-\frac{3{x}^{3}}{{x}^{5}}+\frac{{x}^{2}}{{x}^{5}}}{\frac{\left({x}^{2}-3\right)\left(2{x}^{3}+x-8\right)}{{x}^{5}}}=\underset{x\to \mathrm{\infty }}{lim} \frac{6-\frac{3}{{x}^{2}}+\frac{1}{{x}^{3}}}{\frac{\left({x}^{2}-3\right)}{{x}^{2}}\frac{\left(2{x}^{3}+x-8\right)}{{x}^{3}}}

Simplificamos.

\underset{x\to \mathrm{\infty }}{lim} \frac{6-\frac{3}{{x}^{2}}+\frac{1}{{x}^{3}}}{\frac{\left({x}^{2}-3\right)}{{x}^{2}}\frac{\left(2{x}^{3}+x-8\right)}{{x}^{3}}}=\underset{x\to \mathrm{\infty }}{lim} \frac{6-\frac{3}{{x}^{2}}+\frac{1}{{x}^{3}}}{\left(\frac{{x}^{2}}{{x}^{2}}-\frac{3}{{x}^{2}}\right)\left(\frac{2{x}^{3}}{{x}^{3}}+\frac{x}{{x}^{3}}-\frac{8}{{x}^{3}}\right)}

\underset{x\to \mathrm{\infty }}{lim} \frac{6-\frac{3}{{x}^{2}}+\frac{1}{{x}^{3}}}{\left(\frac{{x}^{2}}{{x}^{2}}-\frac{3}{{x}^{2}}\right)\left(\frac{2{x}^{3}}{{x}^{3}}+\frac{x}{{x}^{3}}-\frac{8}{{x}^{3}}\right)}=\underset{x\to \mathrm{\infty }}{lim} \frac{6-\frac{3}{{x}^{2}}+\frac{1}{{x}^{3}}}{\left(1-\frac{3}{{x}^{2}}\right)\left(2+\frac{1}{{x}^{2}}-\frac{8}{{x}^{3}}\right)}

Ahora, evaluamos el límite. Recordando que \frac{k}{\infty }=0 .

\underset{x\to \mathrm{\infty }}{lim} \frac{6-\frac{3}{{x}^{2}}+\frac{1}{{x}^{3}}}{\left(1-\frac{3}{{x}^{2}}\right)\left(2+\frac{1}{{x}^{2}}-\frac{8}{{x}^{3}}\right)}=\frac{6-0+0}{\left(1-0\right)\left(2+0-0\right)}=\frac{6}{2}=3

Finalmente:

\underset{x\to \mathrm{\infty }}{lim} \frac{6{x}^{5}-3{x}^{3}+{x}^{2}}{\left({x}^{2}-3\right)\left(2{x}^{3}+x-8\right)}=3

Finalmente, seleccionamos al inciso d) como la respuesta correcta.

¿Conoces cuántos puntos necesitas para quedar? Conoce los aciertos por carrera del IPN.

Reactivo 19

Calcular el límite \underset{x\to \mathrm{\infty }}{lim} \frac{x-2}{\sqrt{4{x}^{2}-9}}

1. 0
2. \frac{1}{2}
3. 1
4. \frac{3}{2}

Solución:

Este límite al infinito presenta una indeterminación \infty /\infty  . Dividimos el numerador y denominador por la mayor potencia fuera del radical, es decir: x .

\underset{x\to \mathrm{\infty }}{lim} \frac{x-2}{\sqrt{4{x}^{2}-9}}=\underset{x\to \mathrm{\infty }}{lim} \frac{\frac{x}{x}-\frac{2}{x}}{\frac{\sqrt{4{x}^{2}-9}}{x}}

Introducimos a la x dentro de la raíz aplicando el siguiente artificio: x=\sqrt{{x}^{2}} .

\underset{x\to \mathrm{\infty }}{lim} \frac{\frac{x}{x}-\frac{2}{x}}{\frac{\sqrt{4{x}^{2}-9}}{x}}=\underset{x\to \mathrm{\infty }}{lim} \frac{\frac{x}{x}-\frac{2}{x}}{\frac{\sqrt{4{x}^{2}-9}}{\sqrt{{x}^{2}}}}=\underset{x\to \mathrm{\infty }}{lim} \frac{1-\frac{2}{x}}{\sqrt{\frac{4{x}^{2}}{{x}^{2}}-\frac{9}{{x}^{2}}}}

Simplificando nos queda:

\underset{x\to \mathrm{\infty }}{lim} \frac{1-\frac{2}{x}}{\sqrt{\frac{4{x}^{2}}{{x}^{2}}-\frac{9}{{x}^{2}}}}=\underset{x\to \mathrm{\infty }}{lim} \frac{1-\frac{2}{x}}{\sqrt{4-\frac{9}{{x}^{2}}}}

Evaluamos.

\underset{x\to \mathrm{\infty }}{lim} \frac{1-\frac{2}{x}}{\sqrt{4-\frac{9}{{x}^{2}}}}=\frac{1-0}{\sqrt{4-0}}=\frac{1}{2}

Finalmente:

\underset{x\to \mathrm{\infty }}{lim} \frac{x-2}{\sqrt{4{x}^{2}-9}}=\frac{1}{2}

La respuesta correcta es el inciso b).

Reactivo 20

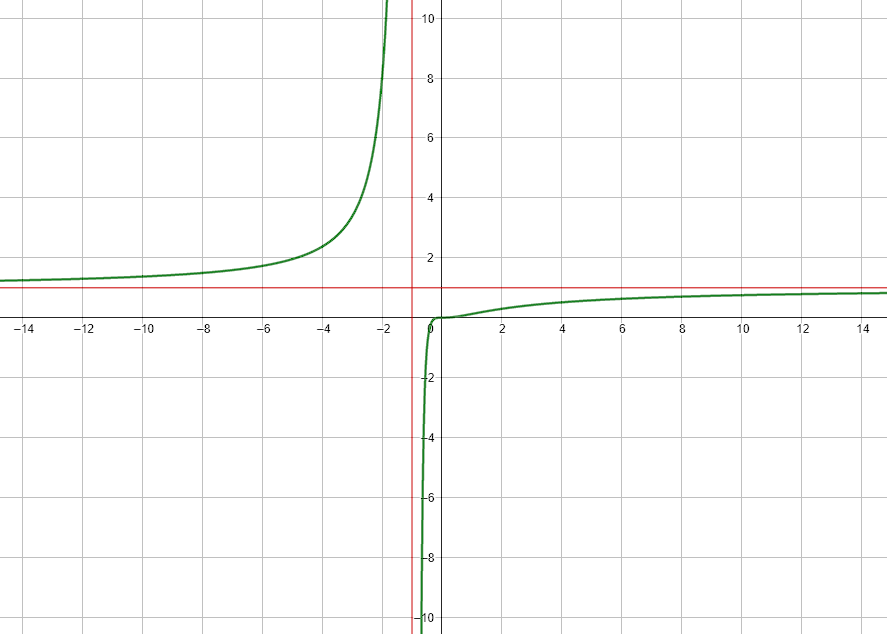
Relacionar los límites de la función h\left(x\right)=\frac{{x}^{3}}{(x+1{)}^{3}} con su valor, de acuerdo con la gráfica siguiente:

1. 1C, 2D, 3B, 4A
2. 1D, 2C, 3A, 4B
3. 1C, 2D, 3A, 4B
4. 1D, 2C, 3B, 4A

Solución:

A partir de los incisos de la columna izquierda, vemos que la función de la figura es f\left(x\right)=\frac{{x}^{3}}{{\left(x+1\right)}^{3}} . Los límites pueden ser resueltos a partir de la gráfica. Vamos a ir analizando cada uno de los límites hasta que tengamos la suficiente información para concluir con la respuesta correcta.

Primer límite.

\underset{x\to \infty }{\mathrm{lim}}\frac{{x}^{3}}{{\left(x+1\right)}^{3}}

Examinando la figura, cuando x crece hacia +\infty  la imagen de la función se acerca cada vez más hacia 1.

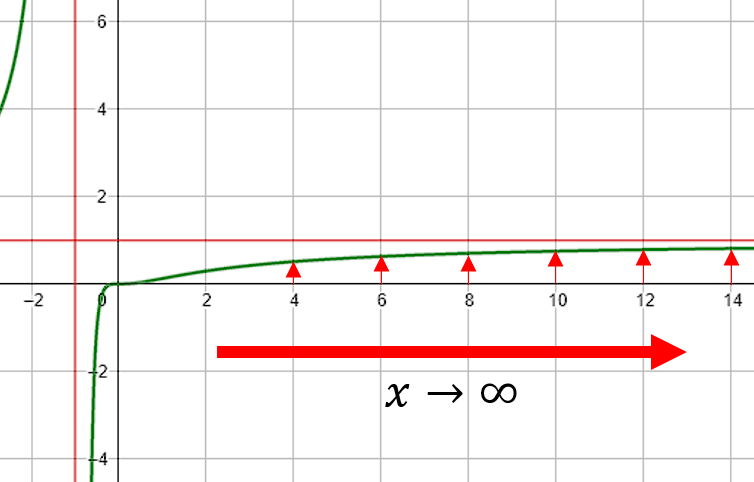
En este caso: 1C. Podemos descartar a los incisos b y d. Por otra parte, los incisos a y c tienen como segundo pareo 2D, esto quiere decir que el pareo decisivo para escoger entre una u otra es el límite 3. Vamos directamente con el tercer límite.

Tercer límite.

\underset{x\to 0}{\mathrm{lim}}\frac{{x}^{3}}{{\left(x+1\right)}^{3}}

A partir de la figura, vemos que la gráfica de la función pasa por el origen. Esto quiere decir que cuando x=0 la imagen de la función es igual a cero. Entonces: 3B. La combinación parcial es: 1C, 2D, 3B, … comparando con las opciones, concluimos que la respuesta correcta es a).