¿Problemas resolviendo la guía interactiva de EXANI II? ¡Llegaste al lugar indicado! Iniciamos la solución de la Guía Interactiva de EXANI II, en la asignatura de probabilidad y estadística. En este tutorial resolveremos desde el reactivo 1 hasta el 12.

Hemos incluido una justificación para las respuestas incorrectas. De esta forma podrás identificar debilidades y entender por qué cierta respuesta es incorrecta.
Estructura del EXANI II
La prueba de ingreso EXANI II está compuesta por dos áreas, cada una con la misma importancia en la nota final:
- Habilidades y conocimientos
- Los módulos específicos
Algunas universidades también aplican una prueba diagnóstico de inglés, la cual no cuenta para aprobar el examen.
Examen de habilidades y conocimientos
La primera parte del EXANI II es obligatoria para los aspirantes de todas las carreras. Está compuesta por 90 reactivos, 60 de Español y 30 de Matemáticas.
La siguiente tabla resume la distribución de los reactivos en la prueba de ingreso EXANI II:
| Área | Reactivos |
|---|---|
| Habilidades y conocimientos | |
| Pensamiento matemático | 30 |
| Comprensión lectora | 30 |
| Redacción indirecta | 30 |
| Módulos de conocimientos específicos | |
| Módulo 1 | 24 |
| Módulo 2 | 24 |
| Subtotal de reactivos | 138 |
| Diagnóstico | |
| Inglés | 30 |
| Total de reactivos | 168 |
Conocimientos específicos
Conocimientos específicos del EXANI II posee un total de 15 módulos en los que se encuentra probabilidad y estadística.
Todos los estudiantes deben responder 2 módulos en esta segunda parte, los cuales varían de acuerdo con la carrera. Es necesario que revises la convocatoria de tu universidad para conocer qué módulos debes estudiar.
| 1. Administración | 9. Física |
| 2. Aritmética | 10. Historia |
| 3. Biología | 11. Literatura |
| 4. Cálculo diferencial e integral | 12. Matemáticas financieras |
| 5. Ciencias de la Salud | 13. Premedicina |
| 6. Derecho | 14. Probabilidad y estadística |
| 7. Economía | 15. Química |
| 8. Filosofía | 16. Psicología |
Temario Probabilidad y estadística EXANI II
En la siguiente tabla te mostramos la distribución de los 24 reactivos de probabilidad y estadística, junto con los temas que van para el examen.
| Subáreas | Temas | Num. de reactivos |
|---|---|---|
| Estadística | Fundamentos: población, muestra y tipos de variables | 12 |
| Frecuencias y sus representaciones | ||
| Medidas descriptivas | ||
| Probabilidad | Elementos: conjuntos y eventos | 12 |
| Cálculo de la probabilidad | ||
| Distribuciones | ||
| Total | 24 |
Recomendaciones para resolver la guía interactiva
Te dejo algunos trucos para sacarle el máximo provecho a la guía EXANI II que puedes tener en cuenta a la hora de estudiar:
- Elimina las distracciones. Ve a un sitio en el que te sientas cómodo o cómoda, coloca tu teléfono en modo avión y mantén cerca de ti lapiceros, borrador y libretas.
- No te enfoques en el resultado, sino en el procedimiento. Coloca toda tu atención en analizar y desglosar los problemas para identificar las herramientas que debes usar. Una buena estrategia conlleva a buenos resultados.
- Lleva el tiempo mientras resuelves la guía. Mide el tiempo durante cada sesión de estudios, buscando acortar el tiempo lo más que puedas antes del examen.
- Si un reactivo parece demasiado difícil, ve al siguiente. Evita caer en frustración mientras estudias, mantener el foco y meditar esos ejercicios difíciles, te permitirán desarrollar capacidades analíticas sólidas.
Reactivo 1
¿Cuántas placas con 3 dígitos y 1 letra se pueden formar sin considerar el 0 ni la letra ñ?
Considere que es posible formar placas con dígitos repetidos.
- 755
- 13 104
- 18 954
Solución:
Iniciamos identificando que deben emplearse permutaciones/variaciones, porque cada placa tendrá un código único formado por los 3 dígitos y la letra. Sabemos que las placas se forman por un total de 4 elementos los cuales son:
- Los números del 1 al 9
- El abecedario sin la ñ
Es decir, tres espacios serán ocupados por 9 posibles números y el restante por una de 26 letras. Debido a que se permite repetir elementos, el total de placas se calcula como:
P=9\cdot 9\cdot 9\cdot 26=18954
Se pueden formar 18954 placas con la configuración mencionada en el enunciado. La respuesta correcta es el inciso c). El error en la opción a) es que se multiplica 9\cdot 9\cdot 9 pero el 26 se suma al resultado, no se multiplica.
Por otro lado, en el inciso b) se considera a los números sin repetición, realizando el cálculo: 9\cdot 8\cdot 7\cdot 26 .
Reactivo 2
En una fábrica de refrigeradores se registraron las unidades vendidas durante 15 días: 9, 10, 11, 8, 9, 10, 10, 7, 4, 15, 9, 8, 8, 6 y 14.
¿Cuál es la frecuencia relativa para 8 unidades vendidas?
- \frac{1}{15}
- \frac{1}{5}
- \frac{8}{15}
Solución:
Primero creamos una tabla de frecuencias, en las que se muestran las cantidades vendidas y la frecuencia absoluta asociada a cada venta.
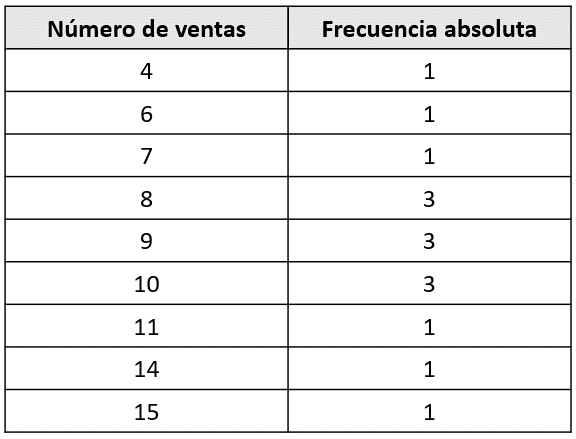
La frecuencia relativa se calcula como el cociente entre la frecuencia absoluta de la clase y el total de elementos del experimento. En este caso n=15 , por lo tanto:
{f}_{8}=\frac{3}{15}=\frac{1}{5}
La respuesta correcta es el inciso b). En la opción a) se toma en cuenta la cantidad total de elementos, pero no se toma la frecuencia absoluta correcta de las 8 ventas.
En la opción c) sucede algo similar, pero en lugar de sustituir la frecuencia de las ventas, se sustituye el número de productos vendidos. Ambos son errores conceptuales.
Reactivo 3
La tabla muestra la distribución de frecuencia del número de piezas producidas por 100 trabajadores de una fábrica.
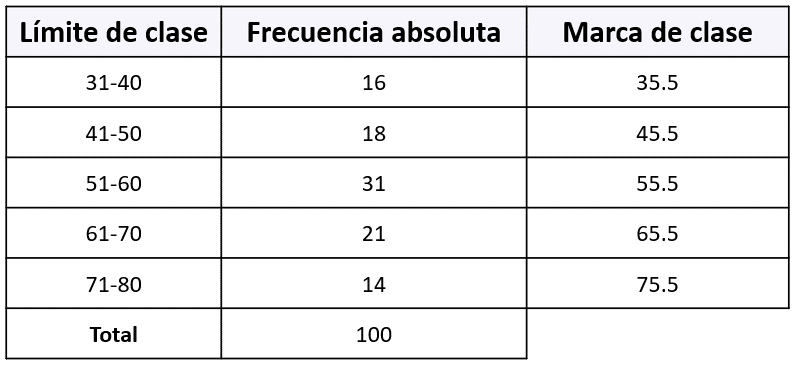
Calcule la media de los datos.
- 20.0
- 55.4
- 55.5
Solución:
Debido a que los datos se encuentran agrupados por intervalos, la media aritmética se calcula como la suma del producto de la marca de clase y la frecuencia, dividido por el total de elementos.
\stackrel{-}{x}=\frac{\sum {x}_{i}\cdot {F}_{i}}{N}
Las marcas de clase se obtienen como la semisuma de los extremos.
{x}_{i}=\frac{L{S}_{i}+L{I}_{i}}{2}
Incluimos el cálculo con la tabla.
Sustituyendo todo en la fórmula:
\stackrel{-}{x}=\frac{\left(35.5\right)\left(16\right)+\left(45.5\right)\left(18\right)+\left(55.5\right)\left(31\right)+\left(65.5\right)\left(21\right)+\left(75.5\right)\left(14\right)}{100}
\stackrel{-}{x}=55.4
La media producida por los 100 trabajadores es de 55.4 piezas. La respuesta correcta es el inciso b). En la opción b) se comete un error conceptual al calcular la media como la suma de las frecuencias divididas por 5.
\stackrel{-}{x}=\frac{16+18+31+21+14}{5}=20
Por otra parte, en la opción c) se calcula la media con las marcas de clase. Esto también es un error conceptual.
\stackrel{-}{x}=\frac{35.5+45.5+55.5+65.5+75.5}{5}=55.5
Reactivo 4
Calcule la varianza de la cantidad de alumnos encuestados en 5 grupos de una escuela, si la cantidad de cada grupo fue 21, 27, 26, 29 y 19.
- 4.2
- 17.8
- 24.4
Solución:
La varianza es un parámetro de dispersión de un conjunto de datos respecto a la media y se calcula como:
{\sigma }^{2}=\frac{\sum {\left({x}_{i}-\stackrel{-}{x}\right)}^{2}}{N-1}
Primero, ordenamos de forma ascendente los datos:
19, 21, 26, 27, 29
Ahora, calculamos la media de los datos.
\stackrel{-}{x}=\frac{19+21+26+27+29}{5}=24.4
Empleamos una tabla para facilitar el cálculo de la media.
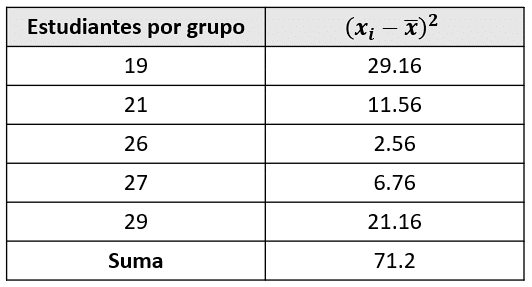
Finalmente:
{\sigma }^{2}=\frac{71.2}{4}=17.8
La respuesta correcta es el inciso b). En la opción a), se confunde la varianza con la desviación típica, aplicando raíz cuadrada a 17.8 , mientras que en la c) se calcula la media de los datos.
Reactivo 5
Se lanza 1 moneda, se tira 1 dado de 6 caras y se elige 1 carta de una baraja que contiene 40.
Determine el espacio muestral.
- 3
- 240
- 480
Solución:
La moneda tiene 2 lados, el dado 6 caras y la baraja 40 cartas, el tamaño del espacio muestral se obtiene como el producto de los lados, las caras y las cartas.
S=\left(2\right)\left(6\right)\left(40\right)=480
El espacio muestral del experimento es de 480 posibles resultados.
La respuesta correcta es el inciso c). En el inciso a) se considera la cantidad de elementos que confirman un resultado del espacio muestral: 1+1+1=3 , pero no cuantifica los posibles resultados que se pueden obtener con la moneda, el dado y la baraja.
El error en el inciso b), consiste en omitir que la moneda tiene 2 caras.
Reactivo 6
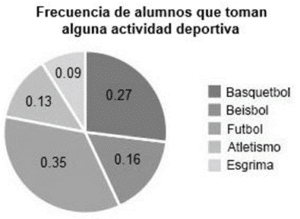
¿En cuál de los siguientes gráficos se utiliza una medida de frecuencia absoluta?
Solución:
Recordemos que la frecuencia absoluta es un número entero que “cuenta” o representa cuántas veces ha ocurrido cierto evento en un experimento aleatorio.
En el gráfico de pastel a), se expresa la frecuencia de actividad de los alumnos como un número decimal, correspondiente a la frecuencia relativa.
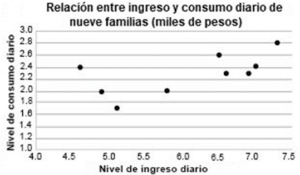
Por otra parte, en el b) se muestra la relación entre dos variables (miles de pesos en ingreso diario vs miles de pesos en gasto diario), una dependiente de otra, por lo que no se representan frecuencias.
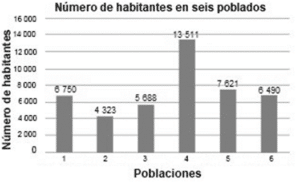
Finalmente, en el gráfico de barras en c) se muestra la cantidad de personas en cada población, correspondiente con la frecuencia absoluta de la muestra.
Reactivo 7
Para llevar el registro de una enfermedad, de un total de 74 personas, se recabaron los datos de personas infectadas por día y se elaboró la siguiente gráfica.
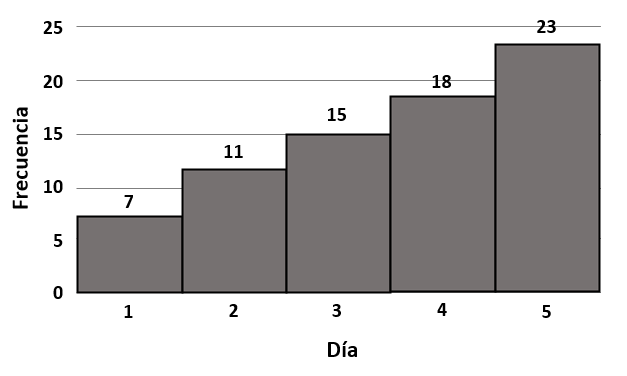
¿Cuál es la frecuencia acumulada en porcentaje, de personas infectadas, hasta antes del cuarto día?
- 20 %
- 45 %
- 69 %
Solución:
Debido a que se solicita la frecuencia acumulada porcentual antes del día 4, debemos calcular la frecuencia acumulada porcentual desde el año 1 hasta el 3.
F{A}_{1-3}=7+11+15=33
Ahora, dividimos este resultado entre el total de personas y multiplicamos por 100.
FA{P}_{1-3}=\frac{33}{74}\cdot 100=44.59\%\approx 45\%
La respuesta correcta es el inciso b). Es equivalente calcular la frecuencia relativa para cada dato y luego sumar desde el día 1 hasta el 3.
En el inciso a) se considera la frecuencia relativa del tercer día, mientras que en el c) se consideran las frecuencias desde el día 1 hasta el 4, pero en enunciado solicita desde el 1 hasta el 3.
Reactivo 8
Un diseñador terminó de elaborar 1 cartel y tiene disponibles 12 colores para iluminarlo.
¿Cuántas combinaciones obtiene si solo utiliza 5 colores diferentes, sin importar el orden?
- 792
- 95 040
- 248 832
Solución:
Debido a que no importa el orden, empleamos la técnica de conteo por combinaciones para resolver el problema:
{C}_{m}^{n}=\frac{m!}{n!\cdot \left(m-n\right)!}
Sustituimos m=12 y n=5 .
{C}_{12}^{5}=\frac{12!}{5!\cdot \left(12-5\right)!}=792
El diseñador puede combinar los 12 colores de 792 formas.
La respuesta correcta es el inciso a). El resultado del inciso b) se obtiene por utilizar permutaciones, pero el enunciado deja claro que no importa el orden. Las permutaciones/variaciones se emplean cuando importa el orden.
Por otro lado, el inciso c) asume que se permite repetir colores y utiliza la fórmula {m}^{n}={12}^{5} .
Reactivo 9
En una urna hay 52 esferas numeradas del 1 al 13 y clasificadas en 4 colores distintos. Si se extrae una de estas, ¿cuál es la probabilidad de obtener el número 4 o el 7, sin importar el color?
- \frac{1}{169}
- \frac{2}{13}
- \frac{11}{52}
Solución:
Iniciemos identificando cómo se distribuyen las 52 esferas en la urna. Tenemos que las mismas se enumeran del 1 al 13 y que se distribuyen en 4 colores, es decir, por cada color hay 13 esferas que van del 1 al 9. Esto da un total de 52 esferas: 13\cdot 4=52 .

Solo nos interesa que salga el 4 o el 7. En el conjunto hay 4 esferas con el 4, al igual que con el 7. Como se mencionó antes, una por cada color. Esto nos da un total de 8 esferas.

Aplicamos la fórmula de probabilidad clásica.
P\left(4\vee 7\right)=\frac{8}{52}=\frac{2}{13}
La respuesta correcta es el inciso b). En el inciso a) en lugar de sumar las probabilidades para el 4 y para el 7 se multiplican, dando como resultado \frac{1}{169} . Por otro lado. En el inciso c) se utiliza la ley de la adición, pero en lugar de utilizar la cantidad de esferas por número, se utiliza el número de las esferas:
P\left(4\vee 7\right)=\frac{4}{52}+\frac{7}{52}=\frac{11}{52}
Reactivo 10
Determine la moda de los datos obtenidos en un estudio socioeconómico aplicado a 15 familias, en el cual se preguntó por el número de habitaciones que tienen en casa y se obtuvieron los siguientes resultados.
7, 3, 2, 3, 3, 6, 3, 7, 6, 6, 8, 4, 3, 8, 7
- 3
- 5
- 6
Solución:
La moda es el o los elementos que más se repiten de un conjunto de datos. Para encontrarla, debemos iniciar ordenando los datos de forma ascendente o descendente.
2, 3, 3, 3, 3, 3, 4, 6, 6, 6, 7, 7, 7, 8, 8
Examinando los datos, el que más se repite es el 3, un total de 5 veces. La respuesta correcta es el inciso a). En el inciso b) se confunde la moda con la media aritmética, mientras que en el c) se calcula la mediana y no la moda.
Reactivo 11
Para conocer la calidad de los tomates en un plantío de 10 ha, el dueño decide recolectar 100 unidades de 2 ha para su análisis. A las 100 unidades se les llama…
- censo
- población
- muestra
Solución:
En estadística, cuando una población es demasiado grande, se extrae una muestra representativa de la población para aplicar el estudio sobre ella y luego extrapolar los resultados al total de elementos.
En el enunciado, el dueño toma una muestra de las 10 ha para aplicar el estudio de calidad. La respuesta correcta es el inciso c).
Un censo se utiliza para contar el total de elementos que conforman una población, mientras que la población representa al total de individuos a estudiar. Estos conceptos no corresponden a la situación planteada por el enunciado.
Reactivo 12
En un estudio de mercado se registra la cantidad de dinero, en pesos, que los clientes gastan en un supermercado. Se eligieron 5 al azar cuyos gastos fueron 252, 259, 261, 248 y 255.
¿Cuál es el valor de la desviación estándar de las cantidades gastadas?
- 5.2
- 10.5
- 27.5
Solución:
Para un conjunto de datos desagrupados que representan la muestra de una población, la desviación estándar se calcula como:
\sigma =\sqrt{\frac{\sum {\left({x}_{i}-\stackrel{-}{x}\right)}^{2}}{N-1}}
Iniciamos obteniendo la media de los datos.
\stackrel{-}{x}=\frac{252+259+261+248+255}{5}=255
Ahora, con ayuda de una tabla calculamos el cuadrado de las diferencias de los datos con la media.
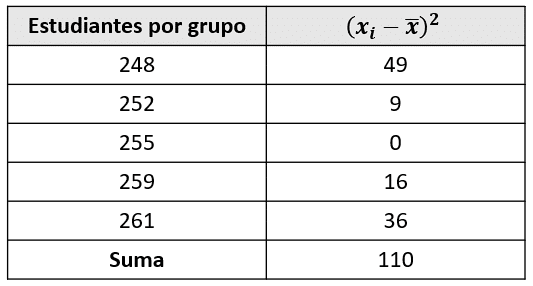
Sustituyendo en la ecuación de la desviación estándar nos queda:
\sigma =\sqrt{\frac{110}{5-1}}=5.24
La desviación estándar entre los gastos fue de 5.24 pesos.
La respuesta correcta es el inciso a). En el inciso b) se realizan los cálculos correctos de la media y el cuadrado de las diferencias, pero no se ha dividido por N-1 . Por otro lado, en el inciso c) se calcula la varianza {\sigma }^{2} no la desviación estándar \sigma .