¡Hola aspirante! Iniciamos la solución de la Guía Interactiva de EXANI II de Ceneval, en la asignatura de pensamiento matemático. En este tutorial resolveremos desde el reactivo 1 hasta el 10.

Además de resolver paso a paso cada reactivo, hemos incluido una justificación para las respuestas incorrectas. De esta forma podrás identificar debilidades y entender por qué cierta respuesta es incorrecta.
Estructura del EXANI II
La prueba de ingreso aplicada por Ceneval se compone por dos áreas con la misma importancia a la hora de cuantificar el resultado final: habilidades y conocimientos y los módulos específicos.
Además, se incluye una prueba diagnóstico de inglés cuyo resultado no repercute en la nota final.
Examen de habilidades y conocimientos
Esta es la primera parte del EXANI II 2023 es obligatoria para los aspirantes de todas las carreras, compuesto por dos asignaturas: Español y Matemáticas.
En la siguiente tabla, te dejo la distribución de los reactivos en la prueba de ingreso EXANI II:
| Área | Reactivos |
|---|---|
| Habilidades y conocimientos | |
| Pensamiento matemático | 30 |
| Comprensión lectora | 30 |
| Redacción indirecta | 30 |
| Módulos de conocimientos específicos | |
| Módulo 1 | 24 |
| Módulo 2 | 24 |
| Subtotal de reactivos | 138 |
| Diagnóstico | |
| Inglés | 30 |
| Total de reactivos | 168 |
Conocimientos específicos
En el área de conocimientos específicos del EXANI II hay un total de 15 módulos. Todos los estudiantes deben resolver 2 módulos en esta segunda parte, los cuales varían de acuerdo con el área a la que pertenece tu carrera.
Es necesario que revises la convocatoria de tu universidad, allí encontrarás toda la información al respecto. Módulos de los conocimientos específicos:
| Módulos Exani II | |
|---|---|
| Administración | Física |
| Aritmética | Historia |
| Biología | Literatura |
| Cálculo diferencial e integral | Matemáticas financieras |
| Ciencias de la salud | Premedicina |
| Derecho | Probabilidad y estadística |
| Economía | Química |
| Filosofía | Psicología |
| C. Experimentales | C. Sociales |
Temario Pensamiento matemático EXANI II
En la siguiente tabla te mostramos la distribución de los 30 reactivos de pensamiento matemático y los temas que van para el examen.
| Subárea | Tema | Núm. de reactivos |
|---|---|---|
| Comprensión de lo matemático | Conexiones | 18 |
| Estimación | ||
| Sentido numérico | ||
| Matematización | Desarrollo de usos | 12 |
| Lenguaje matemático | ||
| Resignificaciones | ||
| Total | 30 | |
Recomendaciones para resolver la guía interactiva
Te dejo algunos trucos para sacarle el máximo provecho a la guía EXANI II 2023 que puedes tener en cuenta a la hora de estudiar:
- Elimina las distracciones. Ve a un sitio en el que te sientas cómodo o cómoda, coloca tu teléfono en modo avión y mantén cerca de ti lapiceros, borrador y libretas.
- No te enfoques en el resultado, sino en el procedimiento. Coloca toda tu atención en analizar y desglosar los problemas para identificar las herramientas que debes usar. Una buena estrategia conlleva a buenos resultados.
- Lleva el tiempo mientras resuelves la guía. Mide el tiempo durante cada sesión de estudios, buscando acortar el tiempo lo más que puedas antes del examen.
- Si un reactivo parece demasiado difícil, ve al siguiente. Evita caer en frustración mientras estudias, mantener el foco y meditar esos ejercicios difíciles, te permitirán desarrollar capacidades analíticas sólidas.
Reactivo 1
Una familia ha realizado un registro del número de kilowatts consumidos en su hogar y el costo de la corriente eléctrica durante 5 meses. Los datos se presentan en el cuadro:
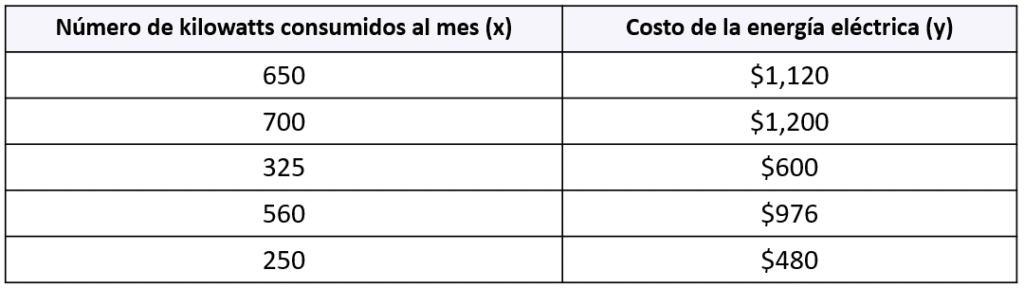
¿Qué modelo representa el costo de la corriente eléctrica, de acuerdo con el número de kilowatts consumidos?
- y = 1.6x + 80
- y = 1.6x – 80
- y = 1.7x + 15
Solución:
En estos casos, hay dos posibles modelos matemáticos para el conjunto de datos: lineal y cuadrático. Si examinamos los incisos, vemos que todas las opciones muestran ecuaciones de rectas, por lo tanto, el modelo tiene que ser una línea recta.
Ecuación punto pendiente de la recta:
y-{y}_{0}=m\left(x-{x}_{0}\right)
Ahora, es necesario calcular la pendiente de la recta y sustituir un punto del conjunto de datos. Se seleccionan los dos primeros puntos de la tabla. Hay que tener en cuenta que la columna de la izquierda corresponde con la variable x , mientras que la derecha con la variable y .
Punto 1: {P}_{1}\left(650, 1120\right) .
Punto 2: {P}_{2}\left(\mathrm{700,1200}\right) .
Se sustituyen las coordenadas en la ecuación de la pendiente:
m=\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}=\frac{1200-1120}{700-650}=\frac{80}{50}=\frac{8}{5}=1.6
Finalmente, se sustituye el valor de la pendiente y un punto (en este caso {P}_{1} ) para obtener la ecuación que describe a los datos.
y-1120=1.6\left(x-650\right)
y=1120+1.6x-1040
y=1.6x+80
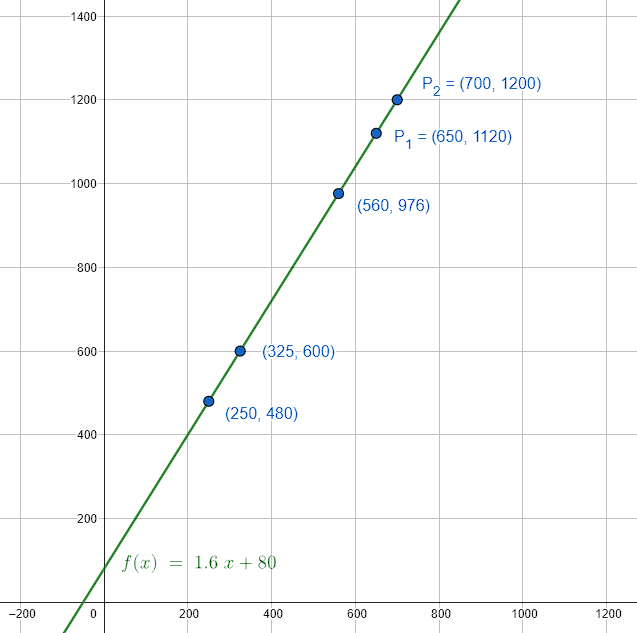
La respuesta correcta es el inciso a). En el caso de seleccionar como respuesta correcta al inciso b), probablemente hayas cometido un error en la ecuación de la línea recta: y+{y}_{0}=m\left(x+{x}_{0}\right) en lugar de y-{y}_{0}=m\left(x-{x}_{0}\right) .
Por otra parte, si consideras como respuesta correcta al inciso c), el error se encuentra en el cálculo de la pendiente. En lugar de dividir la diferencia de las coordenadas m=\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}} , has calculado el cociente de la suma de las coordenadas m=\frac{{y}_{2}+{y}_{1}}{{x}_{2}+{x}_{1}} .
Reactivo 2
Ana construye un reloj en una circunferencia de radio igual a 5 cm y otro en una circunferencia de radio igual a 25 cm. Ana gira la manecilla del primer reloj de la 1:00 a las 5:00 horas y la manecilla del segundo de las 10:00 a las 3:00 horas.
De acuerdo con esta información, ¿cuál afirmación es correcta?
- La manecilla del primer reloj realiza un menor giro que la manecilla del segundo porque cubre un ángulo menor
- La manecilla del primer reloj realiza un menor giro que la del segundo porque es 5 veces menor
- En el primer reloj la manecilla realiza un mayor giro que la del segundo, ya que 5 horas son más que 3
Solución:
Iniciemos teniendo en cuenta que el tiempo medido por los relojes de aguja no tiene nada que ver con su diámetro o con la forma geométrica que posean. Por lo tanto, se puede descartar el inciso b) debido a que comparan los desplazamientos a partir de la relación entre los radios.
El desplazamiento horario de los relojes tiene una relación directa con el desplazamiento angular de las agujas. Mientras más ángulo recorran respecto a un punto, mayor será el intervalo de tiempo medido.
La manecilla del primer reloj hace un desplazamiento horario de: 5-1=4 \mathrm{h}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{s} , mientras que la del segundo reloj se desplaza 5 horas desde las 10 hasta las 3.
Teniendo en cuenta esto, la aseveración correcta es la del inciso a): La manecilla del primer reloj realiza un menor giro que la manecilla del segundo porque cubre un ángulo menor.
En la aseveración del inciso c), solo se toma como punto de comparación el extremo final del desplazamiento y esto no permite evaluar cuántas horas o grados se ha desplazado la aguja desde la posición inicial.
Reactivo 3
Para la función y = 5{x}^{2} - 10x - 25 se obtiene la siguiente gráfica.
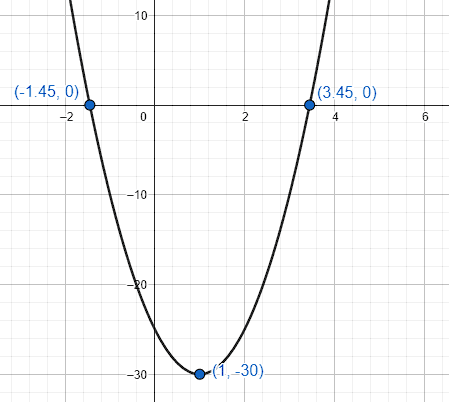
Relacione las ecuaciones que reflejan cambios en los coeficientes con las gráficas que los representan.
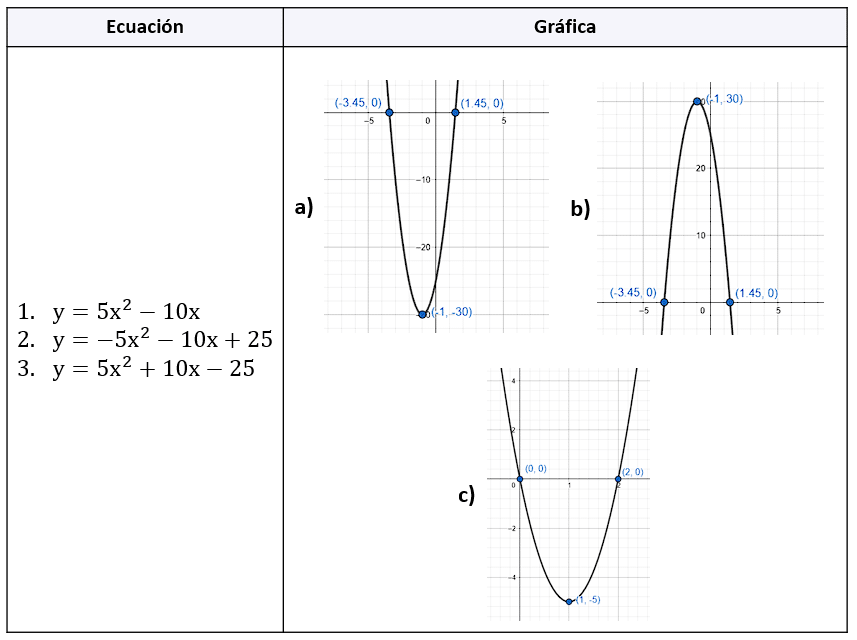
- 1a, 2b, 3c
- 1c, 2a, 3b
- 1c, 2b, 3a
Solución:
Para encontrar la relación correcta entre las ecuaciones y las gráficas, debemos recordar las propiedades de los coeficientes de la ecuación de segundo grado: a{x}^{2}+bx+c .
Si el parámetro a es positivo, la parábola abre hacia arriba, en caso contrario, la parábola abre hacia abajo. Teniendo en cuenta esto, la ecuación del inciso 2 es la única con a<0 y el gráfico b) abre hacia abajo, por lo tanto: 2b.
El parámetro c desplaza a la gráfica hacia arriba cuando es positivo o hacia abajo cuando es negativo. Cuando c=0 , la gráfica de la parábola pasa por el origen. Esto se puede verificar algebraicamente con las raíces del polinomio:
c=0\to a{x}^{2}+bx=0\to x\left(ax+b\right)=0
{x}_{1}=0, {x}_{2}=-\frac{b}{a}
La gráfica del inciso c pasa por el origen y la ecuación 1 no posee valor de c , por lo tanto: 1c. Con las dos respuestas parciales que tenemos hasta ahora: 1c, 2b, … es posible concluir que la respuesta correcta es la opción c).
Si escogiste como respuesta correcta la opción a), no has tenido en cuenta que falta el término independiente en la ecuación 1, mientras que para la ecuación 3 la presencia del término independiente.
Por otra parte, en la opción b) se comete un error en 2a, porque la ecuación 2 tiene el coeficiente a<0 , la parábola debe abrir hacia abajo. Lo mismo ocurre en 3b, se comete un error con el signo del coeficiente a .
Reactivo 4
Considerando los siguientes polinomios:
A= x-3
B=3{x}^{3}-{x}^{2}
C=-4{x}^{2}+2x
¿Cuál es el resultado de la operación que se indica a continuación?
A+2B-C
- 6{x}^{3}+2{x}^{2}-x-3
- 6{x}^{3}+ 3{x}^{2}+3x-3
- 6{x}^{3}-6{x}^{2}-3x-3
Solución:
Se sustituyen las letras A , B y C por las expresiones algebraicas correspondientes.
A+2B-C=x-3+2\left(3{x}^{3}-{x}^{2}\right)-\left(-4{x}^{2}+2x\right)
Ahora, se resuelven las distributivas en el segundo y tercer término de la expresión.
x-3+2\left(3{x}^{3}-{x}^{2}\right)-\left(-4{x}^{2}+2x\right)=x-3+6{x}^{3}-2{x}^{2}-\left(-4{x}^{2}+2x\right)
Simplificando el signo del tercer término:
x-3+6{x}^{3}-2{x}^{2}-\left(-4{x}^{2}+2x\right)=x-3+6{x}^{3}-2{x}^{2}+4{x}^{2}-2x
Se agrupan los términos semejantes y se simplifican las operaciones restantes.
x-3+6{x}^{3}-2{x}^{2}+4{x}^{2}-2x=6{x}^{3}-2{x}^{2}+4{x}^{2}-2x+x-3
6{x}^{3}-2{x}^{2}+4{x}^{2}-2x+x-3=6{x}^{3}+2{x}^{2}-x-3
Finalmente:
A+2B-C=6{x}^{3}+2{x}^{2}-x-3
La respuesta correcta es el inciso a). La opción b) no puede ser la correcta, porque acá se comete un error al resolver la distributiva del tercer término:
x-3+6{x}^{3}-2{x}^{2}-\left(-4{x}^{2}+2x\right)=x-3+6{x}^{3}-2{x}^{2}+4{x}^{2}+2xEn el caso del inciso c), las distributivas se desarrollan de forma correcta pero la simplificación de términos semejantes se hace incorrectamente. Se ha asumido que signos distintos se suman y se mantiene el signo negativo, dando lugar a:
x-3+6{x}^{3}-2{x}^{2}+4{x}^{2}-2x=6{x}^{3}-6{x}^{2}-3x-3
Reactivo 5
¿Qué conjunto de números presenta una desviación estándar mayor?
- {13, 10, 24, 8, 15, 20}
- {16, 16, 9, 12, 12, 16}
- {19, 14, 17, 15, 18, 16}
Solución:
En estadística descriptiva, se utilizan principalmente 3 parámetros para calcular la dispersión de un conjunto de datos: el rango, la varianza y la desviación estándar. El primero es sencillo de calcular, mientras que los otros dos implican cálculos extensos.
Por lo tanto, te recomiendo utilizar el rango, si hay dos conjuntos con rango igual, será necesario recurrir a las otras dos. El rango se calcula como la resta del mayor valor con el menor.
Es posible utilizar el rango para emitir conclusiones, porque mientras mayor rango, mayor ha sido la variabilidad de la variable y, por ende, los datos presentarán mayor diferencia respecto a la media.
Rango del primer conjunto.
{r}_{a}=24-8=16
Rango del segundo conjunto.
{r}_{b}=16-9=7
Rango del tercer conjunto.
{r}_{c}=19-14=5
El conjunto con mayor dispersión y, por ende, mayor desviación típica es el del inciso a). Tanto el inciso b) como el c) son incorrectos, porque los rangos de los conjuntos son más estrechos y, por tanto, la variable tiene menor variabilidad.
Esto se puede observar por la cercanía que tienen los datos unos con otros. Incluso, en el conjunto b) tanto el 12 y como el 16 se ocurren más de una vez. Mientras que el conjunto c) es una secuencia numérica desde el 14 hasta el 19.
Reactivo 6
En la gráfica se muestra el número de pares de zapatos vendidos en una tienda por día hábil.
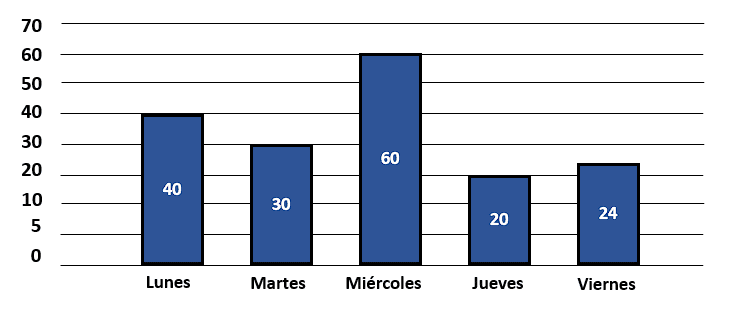
¿Cuál es la media aritmética del número de pares vendidos durante esos días?
- 30
- 35
- 60
Solución:
Para calcular la media de los datos suministrados por la tabla de frecuencias, se divide el total de zapatos vendidos en la semana (correspondientes con la frecuencia de los días) por los 5 días hábiles de la tienda.
\stackrel{-}{x}=\frac{40+30+60+20+24}{5}=\frac{174}{5}=34.8\approx 35
La media de zapatos vendidos en la semana fue de 35 unidades por día hábil.
La respuesta correcta es el inciso b). Si seleccionaste como correcta la opción a), probablemente hayas asociado la media aritmética con la mediana ya que, 30 corresponde con dividir 60 por 2. Por otra parte, la opción c) señala a la frecuencia del día miércoles que se encuentra a la mitad.
Reactivo 7
Silvia va a comprar su uniforme. Una blusa cuesta $171.30, pero le aplicarán 25% de descuento; unos pantalones cuestan $400.25 y le harán 70% de rebaja. Al llegar a la caja para pagar, le comentan que todas las blusas tienen 25% de descuento adicional sobre el precio ya rebajado.
¿Cuál es la cantidad redondeada que Silvia pagará si compra ambas prendas?
- $206.00
- $217.00
- $291.00
Solución:
Para encontrar el precio final a pagar por Silvia, es necesario identificar todas las rebajas que se aplican a cada producto. El total a pagar se calcula como la suma de los precios finales de los productos.
\mathrm{T}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}={\mathrm{P}\mathrm{F}}_{\mathrm{b}}+{\mathrm{P}\mathrm{F}}_{\mathrm{p}}
Por parte de la blusa, se aplican dos descuentos consecutivos, ambos del 25%. Esto de expresa como:
{\mathrm{P}\mathrm{F}}_{\mathrm{b}}=\left(\mathrm{B}\mathrm{l}\mathrm{u}\mathrm{s}\mathrm{a}\right)\left(1-0.25\right)\left(1-0.25\right)
Sustituyendo el precio de la blusa:
{\mathrm{P}\mathrm{F}}_{\mathrm{b}}=\left(171.30\right)\left(1-0.25\right)\left(1-0.25\right)=\$96.35
A los pantalones se les aplica un solo descuento.
{\mathrm{P}\mathrm{F}}_{\mathrm{p}}=\left(\mathrm{P}\mathrm{a}\mathrm{n}\mathrm{t}\mathrm{a}\mathrm{l}\mathrm{ó}\mathrm{n}\right)\left(1-0.7\right)=\left(400.25\right)\left(0.3\right)=\$120
Finalmente:
\mathrm{T}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}=\$96.35+\$120=\$216.35
Redondeando por exceso, Silvia debe pagar 217 pesos por las dos prendas. La respuesta correcta es el inciso b).
Si seleccionaste como respuesta correcta al inciso a), has tenido un error al momento de aplicar los descuentos consecutivos de la blusa. En lugar de multiplicar, los descuentos se han sumado 0.25+0.25=0.5 dando como resultado un precio final para la blusa de \left(171.3\right)\left(0.5\right)=\$85.65 .
En el inciso c) el procedimiento de aplicar los descuentos es correcto, pero en lugar de multiplicar por 1-p donde p es el descuento correspondiente, se multiplica por p .
\mathrm{T}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}=171.3\left(0.25\right)\left(0.25\right)+400.25\left(0.7\right)=\$291
El error se encuentra al omitir restar el descuento al precio inicial del producto.
Reactivo 8
¿Qué figura representa una superficie de 7 unidades cuadradas?
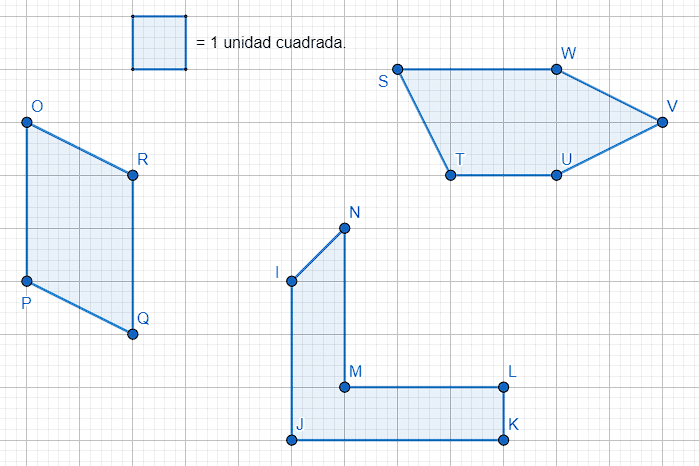
- Figura OPQR
- Figura STUVW
- Figura IJKLMN
Solución:
En este caso, debemos estimar el área de las figuras a partir de que un cuadrado es igual a 1 unidad cuadrada.
Figura ORQP.
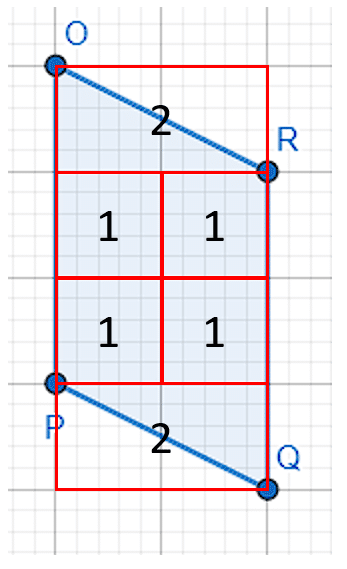
Tanto el triángulo superior como el inferior ocupan la mitad de dos cuadrados, es decir, los triángulos tienen un área de 1 unidad cuadrada cada uno. El área de la figura es:
{A}_{1}=1+1+1+1+1=5 {u}^{2}
Esta figura no tiene un área de 7 unidades cuadradas.
Figura STUVW.
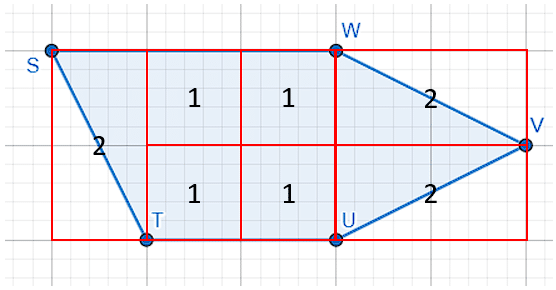
En la figura hay tres triángulos rectángulos, cada uno ocupa dos rectángulos de 2 unidades cuadradas, por lo que, el área asociada a los triángulos es la mitad: 1 unidad cuadrada. Sumando esto con los 4 cuadrados centrales se obtiene:
{A}_{2}=1+1+1+1+1+1+1=7 {u}^{2}
La figura STUVW ocupa 7 unidades cuadradas.
La respuesta correcta es el inciso b). La figura del inciso c): IJKLMN, está conformada por 6 cuadrados enteros y la mitad de otro, es decir, tiene un área de 6.5 unidades cuadradas. No cumple con la condición establecida por el enunciado.
Reactivo 9
Con base en la imagen, seleccione la operación que corresponda al área de la región sombreada en la que BE = EC y EC = DC.
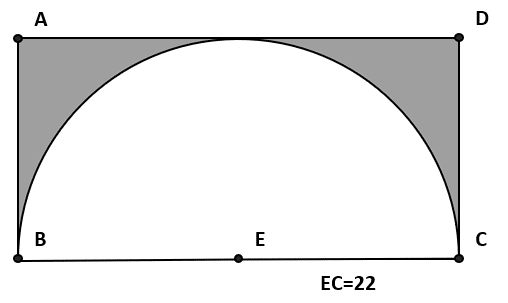
- 968 – 22π
- 968 – 242π
- 968 – 484π
Solución:
El área de la región sombreada se calcula restando el área del cuadrado con el área de semicírculo.
{A}_{s}={A}_{c}-{A}_{sc}
El área del cuadrado es igual al producto de BC con CD.
{A}_{c}=BC\cdot CD
Mientras que el área del semicírculo se obtiene como:
{A}_{sc}=\frac{\pi E{C}^{2}}{2}
Sustituyendo:
{A}_{s}=BC\cdot CD-\frac{\pi E{C}^{2}}{2}
Analizando la figura, vemos que los segmentos BE, EC y CD miden igual que el radio de la circunferencia. Si el segmento EC=22 entonces:
DC=EC=22
BC=BE+EC=44
El área sombreada es igual a:
{A}_{s}=\left(44\right)\left(22\right)-\frac{\pi {\left(22\right)}^{2}}{2}=968-242\pi
La respuesta correcta es el inciso b). Tanto el inciso a) como el inciso c) muestran el valor correcto para el área del rectángulo: 968, pero con errores al momento de representar el área del semicírculo.
En el primer caso (a), en lugar de utilizar la fórmula del área se utiliza la del perímetro. Mientras que en el inciso c se utiliza la fórmula correcta del área de un círculo \pi {r}^{2} pero no se divide entre 2.
Reactivo 10
En un juego de feria se utiliza un dado con el cual es dos veces más probable que salga un número par que uno impar. ¿Cuál es la probabilidad de que al lanzarlo salga el número 5?
- \frac{1}{6}
- \frac{1}{18}
- \frac{1}{9}
Solución:
La probabilidad doble de los números pares se puede representar al duplicarlos en la representación del espacio muestral. Si en un dado normal el espacio muestral es s=\left\{1, 2, 3, 4, 5, 6\right\} , en este caso sería: {s}^{\text{'}}=\left\{1, 2, 2, 3, 4, 4, 5, 6, 6\right\} .
Por lo tanto, hay un total de 9 posibles resultados. La probabilidad de obtener 5 se calcula aplicando la fórmula de probabilidad clásica:
P\left(5\right)=\frac{1}{9}
La respuesta correcta es el inciso c). El inciso a) no puede ser la respuesta correcta, porque se refiere al caso para un dado regular.
Para el inciso b), se ha considerado correctamente que los pares tienen el doble de probabilidades para ser escogidos P\left(\mathrm{p}\mathrm{a}\mathrm{r}\right)=\frac{2}{3} , mientras que los impares P\left(\mathrm{i}\mathrm{m}\mathrm{p}\mathrm{a}\mathrm{r}\right)=\frac{1}{3} . Teniendo esto en cuenta, la probabilidad de extraer 5 se calcula respecto a los 3 números impares, pero en este caso se sustituye el espacio muestral completo.
P\left(5\right)=\frac{\left(\frac{1}{3}\right)}{6}=\frac{1}{18}


