Llegamos a la tercera y última parte del simulacro resuelto de Física correspondiente al módulo 9 del examen de conocimientos específicos para el examen de ingreso EXANI del Ceneval. Vamos por los reactivos del 41 al 50.

Aquí tienes algunos detalles importantes sobre Exani II:
- Desarrollo: Ceneval
- Examen de admisión: Exani II
- Reactivos: 168
- Tipo: Opción múltiple
- Duración: 4 horas y media
- Modalidades: Presencial, en línea y desde casa.
Estos ejercicios, al igual que los anteriores, tienen la misma estructura y abarcan los temas de la prueba real. Resuélvelos por tu cuenta antes de mirar la solución, obtener una buena calificación depende del esfuerzo y la energía que inviertas durante tu preparación.
Estructura del Exani II
El Exani II consta de dos partes, la primera abarca reactivos de conocimiento general, mientras que la segunda, aborda temas de conocimiento específicos que varían en función de la carrera a la cual apliques.
Para conocer a detalle la estructura de la prueba, consulta la siguiente tabla:
| Área | Reactivos |
|---|---|
| Habilidades y conocimientos | |
| Pensamiento matemático | 30 |
| Comprensión lectora | 30 |
| Redacción indirecta | 30 |
| Módulos de conocimientos específicos | |
| Módulo 1 | 24 |
| Módulo 2 | 24 |
| Subtotal de reactivos | 138 |
| Diagnóstico | |
| Inglés | 30 |
| Total de reactivos | 168 |
Temario de Física
A continuación desglosamos todos los temas que forman parte del módulo de conocimientos específicos de Física del Exani II:
- Subárea: Mecánica
- Sistemas de fuerzas coplanares concurrentes y distribuidos
- Elementos que intervienen en el movimiento circular uniforme
- Cálculo de fuerza centrípeta
- Variables relacionadas con el trabajo rotacional y la energía cinética rotacional
- Conservación del momento angular
- Ley de la conservación de la cantidad de movimiento
- Tipos de choque y variables relacionadas
- Subárea: Óptica, ondas y electromagnetismo
- Sistemas de objetos que interactúan a través de sus campos magnéticos
- Generación de fuerza magnética
- Sistemas de fuerzas entre corrientes
- Sistemas conductores que generan campos magnéticos
- Tipos y variables que intervienen en el movimiento armónico simple
- Clasificación, componentes y representación gráfica de ondas
- Aplicación tecnológica de fenómenos ondulatorios
- Tipos de lente
- Características y parámetros que intervienen en los fenómenos ópticos
Ejercicios de Física
Al finalizar este simulacro, habrás repasado todos los temas de física que van para el examen, poniendo en práctica estos conocimientos con ejercicios similares a los de la prueba real.
Reactivo 41
Se tiene un péndulo simple con una longitud en la cuerda de 1 metro, calcule:
- La velocidad angular del péndulo
- La frecuencia de oscilación del péndulo
Nota: emplee g=10 \mathrm{m}/{\mathrm{s}}^{2}
- \sqrt{10}\frac{\mathrm{r}\mathrm{a}\mathrm{d}}{\mathrm{s}},\mathrm{ }\frac{\sqrt{10}}{2\pi } \mathrm{H}\mathrm{z}
- 1\frac{\mathrm{r}\mathrm{a}\mathrm{d}}{\mathrm{s}},\mathrm{ }\frac{1}{2\pi } \mathrm{H}\mathrm{z}
- 3\frac{\mathrm{r}\mathrm{a}\mathrm{d}}{\mathrm{s}},\mathrm{ }\frac{3}{2\pi } \mathrm{H}\mathrm{z}
Solución:
Un movimiento armónico simple es aquel que ocurre periódicamente y con la misma amplitud, se trata de sistemas aislados donde no hay presencia de roces o fuerzas disipativas (no son sistemas reales).
El péndulo simple (para oscilaciones cortas), tiene como frecuencia angular la siguiente ecuación:
\omega =\sqrt{\frac{g}{L}}
Sustituyendo nos queda:
\omega =\sqrt{\frac{10 \mathrm{m}/{\mathrm{s}}^{2}}{1 \mathrm{m}}}=\sqrt{10} \mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}
La frecuencia de oscilación se calcula a partir de la frecuencia angular:
f=\frac{\omega }{2\pi }
Sustituyendo:
f=\frac{\sqrt{10} \mathrm{r}\mathrm{a}\mathrm{d}/\mathrm{s}}{2\pi }=\frac{\sqrt{10}}{2\pi } \mathrm{H}\mathrm{z}
Comparando con las opciones, la respuesta correcta es la a).
Reactivo 42
Relacione el sistema con el tipo de movimiento ondulatorio al que pertenece.

- a12, b3
- a2, b13
- a1, b23
Solución:
Para responder correctamente esta pregunta, debemos identificar como se propaga la ondulación a lo largo del eje de la onda. Recordemos que un movimiento ondulatorio es longitudinal si ocurre perpendicular a la dirección de propagación. Por otra parte, es transversal si ocurre paralela a la dirección de propagación.
Teniendo en cuenta estas definiciones, procedemos a analizar los sistemas de la columna derecha.
Onda en una cuerda.
En este caso, los puntos de la onda oscilan perpendicularmente al eje de propagación. Concluimos que pertenece al grupo a.
Onda sonora en el aire.
Las ondas sonoras se propagan desde la fuente hasta un receptor, contrayendo y expandiendo el aire a su alrededor. Esto corresponde a un movimiento ondulatorio transversal, es decir, pertenece al grupo b.
Onda en un muelle.
De la misma forma que la onda en el are, una onda que se propaga a lo largo de un muelle contrae y expande al mismo para ir de un punto a otro a lo largo del resorte. Diremos entonces que pertenece al grupo b.
Uniendo todas las respuestas, concluimos que:
a1, b23.
Comparando con las opciones, seleccionamos como correcta la c).
Reactivo 43
La interferencia entre ondas es constructiva si ______ la amplitud de la resultante y destructiva si ________ la amplitud de la resultante.
- Disminuye – Aumenta
- Aumenta – Disminuye
- Se cancelan – Se adicionan
Solución:
Cuando dos ondas que se propagan en un mismo medio y se encuentran en algún punto, estas interactúan, lo que se denomina interferencia, y pueden pasar dos cosas:
- La amplitud de la onda resultante es mayor que la amplitud de las ondas iniciales
- La amplitud de la resultante es menor que la de las ondas iniciales
A la primera se le denomina interferencia constructiva y a la segunda interferencia destructiva. En base a estas definiciones, concluimos completando la frase de la siguiente manera:
La interferencia entre ondas es constructiva si Aumenta la amplitud de la resultante y destructiva si Disminuye la amplitud de la resultante.
Escogemos como respuesta correcta la opción b).
Reactivo 44
¿En qué dirección deben colocarse los hilos de un polarizador para eliminar la onda electromagnética transversal de color azul?
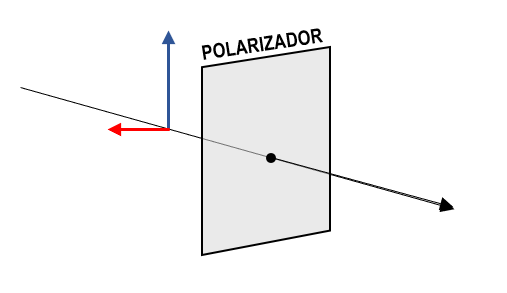
- En dirección horizontal
- En dirección vertical
- En diagonal
Solución:
La polarización de una onda electromagnética, se refiere al “filtrado” de las componentes que oscilan en una dirección diferente a la de interés. Por ejemplo, la siguiente figura muestra la representación de tres componentes del campo eléctrico en una onda electromagnética. Por convención y a modo de simplificación, solo se trabaja con el campo eléctrico.
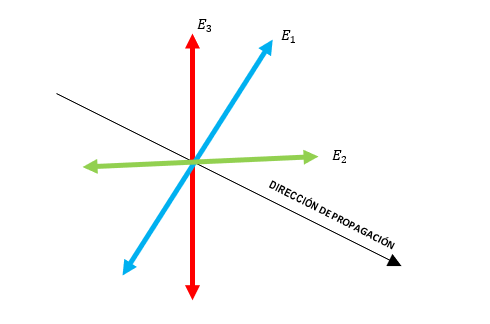
Para que un polarizador lineal de hilo (como el que se solicita en el ejercicio) “filtre” una componente específica de la onda, dichos hilos deben orientarse en la misma dirección que la onda que queremos mantener. En el caso de nuestro problema, en la dirección horizontal para eliminar la componente de color azul.
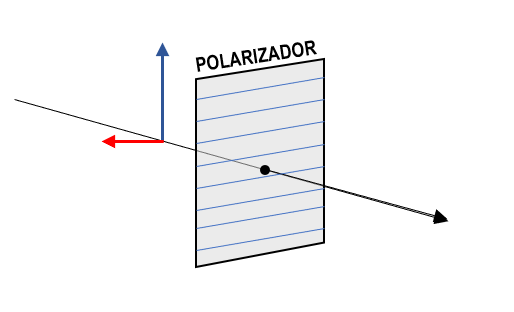
Concluimos indicando que la respuesta correcta se encuentra en el inciso a), dirección horizontal.
Reactivo 45
María desea enviar un mensaje de texto a su amiga Julia. Si María se encuentra a 20 metros de la torre telefónica y Julia a 40 metros de la misma, ¿en cuánto tiempo llega el mensaje de un punto a otro?
La velocidad de la luz en el vacío es: c=3\bullet {10}^{8} \mathrm{m}/\mathrm{s} .
- 2 segundos
- 2 milisegundos
- 200 nanosegundos
Solución:
Para resolver este problema, debemos calcular el tiempo que tardaría el mensaje en ir desde el celular de María a la torre y de allí al celular de Julia. Debemos emplear la siguiente ecuación:
c=\frac{\mathrm{\Delta }x}{t}
Donde: \mathrm{\Delta }x es la distancia que debe recorrer la onda electromagnética y t es el tiempo que va a tardar. Despejamos de la ecuación el tiempo.
t=\frac{\mathrm{\Delta }x}{c}
El tiempo total es la suma del tiempo que tarda desde María a la torre y de la torre a Julia.
t={t}_{M}+{t}_{J}
t=\frac{\mathrm{\Delta }{x}_{M}}{c}+\frac{\mathrm{\Delta }{x}_{J}}{c}
Sustituimos los valores dados.
t=\frac{20\mathrm{ }\mathrm{m}}{3\bullet {10}^{8} \mathrm{m}/\mathrm{s}}+\frac{40 \mathrm{m}}{3\bullet {10}^{8} \mathrm{m}/\mathrm{s}}=20\bullet {10}^{-8} \mathrm{s}
El mensaje tarda 200 nanosegundos en ir de un celular a otro.
Concluimos que la respuesta correcta es la c).
Reactivo 46
La óptica geométrica estudia los fenómenos y elementos ópticos mediante el empleo de __________________, mientras que la óptica de onda se basa en la naturaleza _________ de la luz.
- Líneas rectas y geometría plana – ondulatoria
- Partículas – fotones
- Química analítica – electromagnetismo
Solución:
La óptica geométrica u “óptica clásica” trata a la luz como un conjunto de rayos que se propagan e interactúan con los objetos, siendo reflejados, absorbidos o desviados. Para ello, se emplean rectas y geometría para encontrar elementos de interés como puntos focales o rayos de luz.
Por otro lado, la óptica ondulatoria emplea todo el potencial de la teoría ondulatoria y, más específicamente, de la teoría electromagnética para describir el comportamiento de la luz.
Considerando estas dos definiciones, queda claro que las frases que completan la oración correctamente son:
La óptica geométrica estudia los fenómenos y elementos ópticos mediante el empleo de líneas rectas y geometría plana, mientras que la óptica de onda se basa en la naturaleza ondulatoria de la luz.
Concluimos entonces que la respuesta correcta es la opción a).
Reactivo 47
En una lente convergente, ¿en qué posición debe colocarse un objeto para que la imagen formada sea mayor que el objeto?
- Entre F y 2F
- En 2F
- Menor que F
Solución:
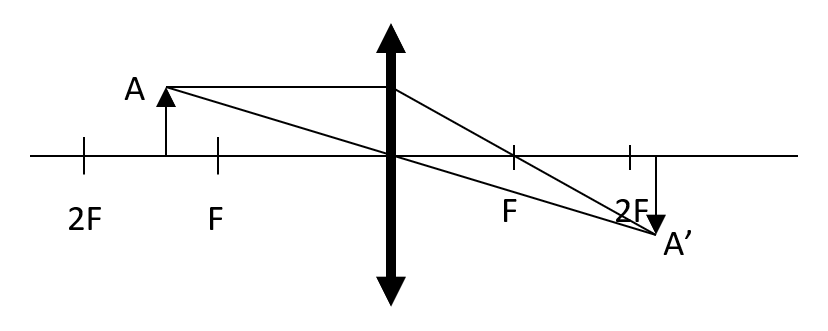
Las lentes convergentes son aquellas que concentran en un punto los rayos que inciden paralelos al eje principal caracterizándose por ser más gruesas en el centro que en los bordes. En dichas lentes, los rayos luminosos que inciden en ellas paralelos al eje principal se reúnen después de atravesar la lente en un punto llamado foco principal de la lente.
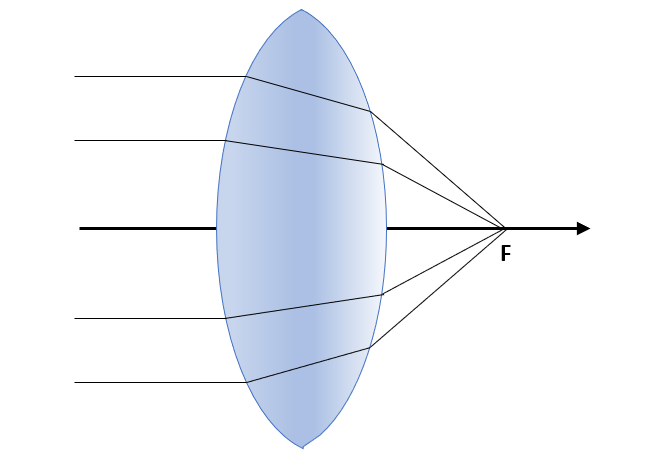
Cuando el objeto está situado entre el foco y el doble de la distancia focal, la imagen que se forma es real, invertida, de mayor tamaño y situada más allá de 2F. Concluimos entonces que la respuesta correcta es la a).
Reactivo 48
Dada las siguientes aseveraciones, indique cuál de ellas es verdadera.
- Las lentes convergentes son más gruesas en los bordes y las divergentes en el centro
- Una lente es un medio transparente limitada por dos caras, de las cuales, al menos una es curva
- La luz blanca puede formarse el combinar luz azul y amarilla
- 3
- 2
- 1
Solución:
La primera frase es incorrecta, realmente, las lentes convergentes son gruesas en el centro y las divergentes gruesas en los bordes.
La segunda frase es cierta. Es precisamente la definición de una lente. En esta línea de ideas, la tercera es falsa, tanto por descarte como porque la luz blanca se forma con todos los colores del arcoíris.
Concluimos que la respuesta correcta es la b).
Reactivo 49
Si el índice de refracción absoluto del agua es {n}_{1}=1.33 y el del hielo es {n}_{2}=1.31 , calcule el índice de refracción relativo del agua respecto del hielo.
- 0.98
- 0.88
- 1.01
Solución:
El índice de refracción relativo a dos medios, es la relación o cociente entre sus índices de refracción absoluto. Si {n}_{1} es el IRA en el primer medio y {n}_{2} es el IRA en el segundo medio, {n}_{1-2} es el índice de refracción relativo del medio 1 respecto al medio 2.
{n}_{1-2}=\frac{{n}_{1}}{{n}_{2}}
Sustituimos los valores dados para el agua y el hielo.
{n}_{1-2}=\frac{1.33}{1.31}=1.01
Comparando con las opciones del problema, indicamos que la respuesta correcta es la opción c).
Reactivo 50
Un rayo luminoso proviene del aire e incide en una lámina de vidrio. Si el ángulo de incidencia es 60° y el de refracción es 30°. Calcular: el índice de refracción absoluto del vidrio y la velocidad de la luz al propagarse por el vidrio.
Considere que: \mathrm{sin}30°=0.5, \mathrm{sin}60°=0.87, c=300\bullet {10}^{6} \mathrm{m}/\mathrm{s} .
- {n}_{2}=1.74, {V}_{s}=172.41\bullet {10}^{4} \mathrm{m}/\mathrm{s}
- {n}_{2}=0.74, {V}_{s}=172.41\bullet {10}^{5} \mathrm{m}/\mathrm{s}
- {n}_{2}=1.74, {V}_{s}=172.41\bullet {10}^{6} \mathrm{m}/\mathrm{s}
Solución:
Para calcular los valores solicitados, debemos recurrir a la segunda Ley de Snell para la refracción de la luz, que dice que el cociente entre el seno del ángulo de incidencia y el seno del ángulo de refracción, al que llamaremos índice de refracción del segundo medio respecto al primero.
\frac{\mathrm{sin}{\theta }_{i}}{\mathrm{sin}{\theta }_{r}}={n}_{2-1}
Debido a que el primer medio es el aire, el cual tiene como índice de refracción aproximadamente la unidad, podemos despejar directamente el IRA da la lámina de vidrio.
\frac{{n}_{1}}{{n}_{2}}=\frac{\mathrm{sin}{\theta }_{i}}{\mathrm{sin}{\theta }_{r}}\to {n}_{2}=\frac{\mathrm{sin}{\theta }_{r}}{\mathrm{sin}{\theta }_{i}}
{n}_{2}={n}_{1}\frac{\mathrm{sin}{\theta }_{r}}{\mathrm{sin}{\theta }_{i}}=\left(1\right)\frac{0.87}{0.5}=1.74
Ahora, aplicando la definición del IRA podemos obtener la velocidad de propagación de la luz en el vidrio.
{n}_{2}=\frac{c}{{V}_{s}}\to {V}_{s}=c/{n}_{2}
{V}_{s}=\frac{300\bullet {10}^{6} \mathrm{m}/\mathrm{s}}{1.74}=172.41\bullet {10}^{6} \mathrm{m}/\mathrm{s}
Comparando nuestros resultados con las opciones, concluimos que la respuesta correcta es la c).


