En este tutorial vamos a resolver los reactivos del 31 al 40, correspondientes a la segunda parte de los ejercicios de Física del módulo 9 del examen de conocimientos específicos para el examen de ingreso EXANI.

Recuerda desarrollarlos por tu cuenta antes de ver la solución. Con este simulacro puedes acercarte a los ejercicios que saldrán en la prueba real.
Estructura del Exani II
El nuevo Exani II consta de dos partes, la primera se enfoca en conocimientos generales como pensamiento matemático, comprensión lectora y redacción indirecta.
La segunda parte se enfoca en áreas de conocimiento específico que varían de acuerdo a tu carrera.
En la siguiente tabla podrás ver la estructura del Exani II de manera detallada:
| Área | Reactivos |
|---|---|
| Habilidades y conocimientos | |
| Pensamiento matemático | 30 |
| Comprensión lectora | 30 |
| Redacción indirecta | 30 |
| Módulos de conocimientos específicos | |
| Módulo 1 | 24 |
| Módulo 2 | 24 |
| Subtotal de reactivos | 138 |
| Diagnóstico | |
| Inglés | 30 |
| Total de reactivos | 168 |
Temario de Física
Física es uno de los 16 módulos de conocimiento específico que pueden aparecer en tu examen de ingreso, y se enfoca principalmente en dos subáreas. A continuación podrás ver la lista completa de temas que puedes encontrar en esta parte del examen.
- Subárea: Mecánica
- Sistemas de fuerzas coplanares concurrentes y distribuidos
- Elementos que intervienen en el movimiento circular uniforme
- Cálculo de fuerza centrípeta
- Variables relacionadas con el trabajo rotacional y la energía cinética rotacional
- Conservación del momento angular
- Ley de la conservación de la cantidad de movimiento
- Tipos de choque y variables relacionadas
- Subárea: Óptica, ondas y electromagnetismo
- Sistemas de objetos que interactúan a través de sus campos magnéticos
- Generación de fuerza magnética
- Sistemas de fuerzas entre corrientes
- Sistemas conductores que generan campos magnéticos
- Tipos y variables que intervienen en el movimiento armónico simple
- Clasificación, componentes y representación gráfica de ondas
- Aplicación tecnológica de fenómenos ondulatorios
- Tipos de lente
- Características y parámetros que intervienen en los fenómenos ópticos
Ejercicios de Física
Vamos con la segunda parte del simulacro de Física para EXANI. Una vez hayas resuelto los problemas, analiza el procedimiento, identifica las posibles fallas y puntos de mejora para acortar el tiempo.
Reactivo 31
Se denomina _____ a la magnitud vectorial cuyo módulo permite medir la acción de una fuerza \overrightarrow{F} durante un intervalo de tiempo \mathrm{\Delta }t .
- Trabajo
- Energía
- Impulso
Solución:
En mecánica, existen diferentes magnitudes que permiten describir las interacciones entre cuerpos para determinadas condiciones. Cuando una fuerza no conocida actúa en un intervalo de tiempo sobre un cuerpo y dicho intervalo es pequeño, entonces se mide el producto el cual se define como impulso, magnitud que describe la interacción de la fuerza con la masa.
\overrightarrow{I}=\overrightarrow{F}\bullet \mathrm{\Delta }t
Concluimos entonces que la palabra que completa correctamente la frase es impulso. La respuesta correcta es la c).
Se denomina impulso a la magnitud vectorial cuyo módulo permite medir la acción de una fuerza \overrightarrow{F} durante un intervalo de tiempo \mathrm{\Delta }t .
Reactivo 32
Calcule la fuerza promedio que adquiere una pelota de beisbol al entrar en contacto con el bate. Se sabe que la bola llega con una velocidad horizontal de 40 \mathrm{m}/\mathrm{s} al home plate y sale disparada a 60 \mathrm{m}/\mathrm{s} en sentido contrario. El contacto se realizó durante 5 milisegundos y la masa de la pelota es de 0.15 \mathrm{k}\mathrm{g} .
- 1200 N
- 3000 N
- 100000 N
Solución:
Para calcular la fuerza promedio solicitada, debemos encontrar la magnitud física que nos permita relacionar los datos del enunciado con nuestra incógnita. El impulso y la variación de momento lineal se encuentran proporcionalmente relacionadas a través de la siguiente ecuación:
\overrightarrow{I}=\mathrm{\Delta }\overrightarrow{P}
Además, la variación del momento lineal es igual a:
\mathrm{\Delta }\overrightarrow{P}={\overrightarrow{P}}_{f}-{\overrightarrow{P}}_{i}=m\left({\overrightarrow{v}}_{f}-{\overrightarrow{v}}_{i}\right)
Calculemos la variación del momento lineal con los datos suministrados por el enunciado. Recordemos que la velocidad inicial va en dirección positiva y la velocidad final en dirección negativa, en la componente horizontal.
\mathrm{\Delta }\overrightarrow{P}=\left(0.15 \mathrm{k}\mathrm{g}\right)\left(-60 \mathrm{m}/\mathrm{s}-40 \mathrm{m}/\mathrm{s}\right)\widehat{i}=-15 \mathrm{k}\mathrm{g}\frac{\mathrm{m}}{\mathrm{s}}\widehat{i}
Por otra parte, el impulso es igual al producto de la fuerza promedio por el intervalo de tiempo.
\overrightarrow{I}=\overrightarrow{F}\bullet \mathrm{\Delta }t=\mathrm{\Delta }\overrightarrow{P}
De esta ecuación despejamos la fuerza.
\overrightarrow{F}=\frac{\mathrm{\Delta }\overrightarrow{P}}{\mathrm{\Delta }t}=\frac{-15 \mathrm{k}\mathrm{g}\frac{\mathrm{m}}{\mathrm{s}}\widehat{i}}{0.005 \mathrm{s}}=-3000 \mathrm{N}\mathrm{ }\widehat{i}
La magnitud de la fuerza promedio que imprime el bate sobre la bola es de 3000 Newtons. Indicamos como respuesta correcta la opción b).
Reactivo 33
Si la magnitud de la fuerza eléctrica entre dos cargas puntuales {q}_{1} y {q}_{2} es 40 Newtons, ¿Cuánto vale ahora la fuerza si la distancia se reduce a la mitad?
- 10 N
- 80 N
- 160 N
Solución:
Para resolver este problema, debemos aplicar la Ley de Coulomb y relacionar las ecuaciones de la primera fuerza y primera distancia con la segunda fuerza y distancia. Recordemos que:
{F}_{e}=\frac{k{q}_{1}{q}_{2}}{{d}^{2}}
Para la distancia y fuerza uno.
{F}_{e1}=\frac{k{q}_{1}{q}_{2}}{{d}_{1}^{2}}
Para la distancia y fuerza dos.
{F}_{e2}=\frac{k{q}_{1}{q}_{2}}{{d}_{2}^{2}}
Dividimos ambas ecuaciones.
\frac{{F}_{e1}}{{F}_{e2}}=\frac{\frac{k{q}_{1}{q}_{2}}{{d}_{1}^{2}}}{\frac{k{q}_{1}{q}_{2}}{{d}_{2}^{2}}}=\frac{{d}_{2}^{2}}{{d}_{1}^{2}}
\frac{{F}_{e1}}{{F}_{e2}}=\frac{{d}_{2}^{2}}{{d}_{1}^{2}}
Si la distancia 2 es la mitad que la distancia 1.
{d}_{2}=\frac{{d}_{1}}{2}
Sustituimos y despejamos la fuerza {F}_{e2} .
\frac{{F}_{e1}}{{F}_{e2}}=\frac{{d}_{1}^{2}}{4{d}_{1}^{2}}
{F}_{e2}=4{F}_{e1}
\therefore {F}_{e2}=4\left(40 \mathrm{N}\right)=160 \mathrm{N}
La fuerza entre las cargas al disminuir la distancia a la mitad pasa de 40 N a 160 N. Comparando con las opciones del problema, la respuesta correcta es la c).
Reactivo 34
Calcular la fuerza magnética que experimenta una carga de 0.5 C que se desplaza a una rapidez constante de 2 m/s con un ángulo de 30° respecto del campo magnético. Considere la intensidad del campo igual a 2 \mathrm{T} .
- 1 N
- 2 N
- 4 N
Solución:
Recordemos la definición operacional de la fuerza eléctrica experimentada por una carga en movimiento:
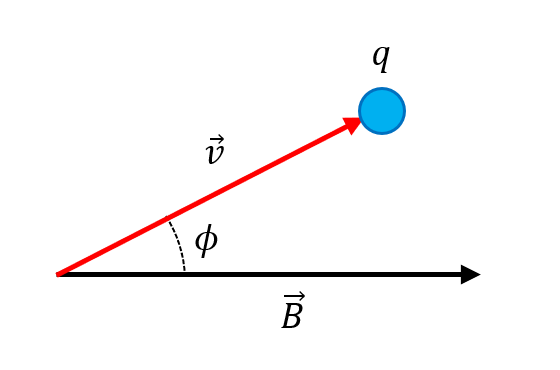
F=\left|q\right|vB\mathrm{s}\mathrm{e}\mathrm{n}\varphi
En este caso, q es la carga, v la rapidez, B la intensidad del campo y \varphi el ángulo entre el campo y la velocidad. El enunciado nos da el valor de cada una de las variables, solo queda sustituir.
F=\left(0.5 \mathrm{C}\right)\left(2\frac{m}{s}\right)\left(2 \mathrm{T}\right)\mathrm{sen}\left(30°\right)=1 \mathrm{N}
La fuerza que experimenta la carga es de 1 N.
Comparando con las opciones, la respuesta correcta es la a).
Reactivo 35
La ley de __________ permite conocer la intensidad del campo magnético _____ en las inmediaciones de un conductor, a través del cual, circula una corriente I .
- Faraday Lenz
- Biot y Savart
- Bose Einstein
Solución:
Cerca de 1820, los físicos franceses Jean Biot y Félix Savart, enunciaron una ley que permite calcular la intensidad del campo magnético generado por un conductor a través del cual, circula una corriente. Dicha ley se enuncia como:
La intensidad del campo magnético generado por un elemento de corriente es directamente proporcional a la intensidad de la corriente e inversamente proporcional al cuadrado de la distancia al elemento de corriente.
El elemento de corriente es un diferencial de longitud del cable por el que circula la corriente, genera un campo magnético circular concéntrico al conductor que interactúa en el punto de medición. Teniendo en cuenta todo lo anterior, la frase se completa correctamente como:
La ley de Biot y Savart permite conocer la intensidad del campo magnético circular en las inmediaciones de un conductor, a través del cual, circula una corriente I .
Respuesta correcta: b).
Reactivo 36
Relacione la aplicación (máquina eléctrica) con el principio electromagnético en el que se basa su funcionamiento.
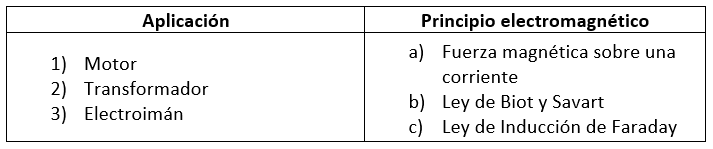
- 1a, 2b, 3c
- 1a, 2c, 3b
- 1c, 2a, 3b
Solución:
Para encontrar la combinación correcta, vamos a analizar cada aplicación en la columna izquierda para relacionarla con un principio electromagnético en la columna derecha.
Motor eléctrico.
Se trata de un bobinado de espiras de alambre sobre un material ferromagnético que se introducen en un campo magnético. Cuando circula una corriente por las espiras, las cargas que constituyen a la corriente experimentan una fuerza debido al campo magnético.
Esta fuerza lineal y perpendicular sobre las espiras se aprovecha de forma aditiva para producir un par de torción en el eje del motor. El principio en este caso es la fuerza magnética sobre una corriente.
1a.
Transformador.
Cuando dos bobinas dispuestas sobre un mismo núcleo ferromagnético y una de ellas se conecta a una fuente que produce un campo magnético variable en el tiempo, dicho campo viaja por el núcleo hasta la otra bobina, induciendo en esta una tensión proporcional a su número de vueltas.
En este caso, el principio electromagnético es la Ley de inducción magnética de Faraday.
2c.
Electroimán.
Si se enrrolla alambre conductor en forma de espira en un núcleo de radio pequeño comparado con su longitud y se hace circular por el alambre una corriente, se origina un campo magnético en el interior de la bobina muy similar al de un imán natural.
Si el núcleo de la bobina es de un material ferromagnético, el campo en su interior se intensifica gracias a que dicho material concentra las líneas de campo. El principio que permite describir esta aplicación de la Ley de Biot y Savart.
3b.
Uniendo todas las respuestas nos queda: 1a, 2c, 3b. Comparando con las opciones, seleccionamos como correcta la b).
Reactivo 37
Dado el circuito de la figura, calcule:
- La resistencia equivalente del arreglo
- La potencia total que consume de la fuente
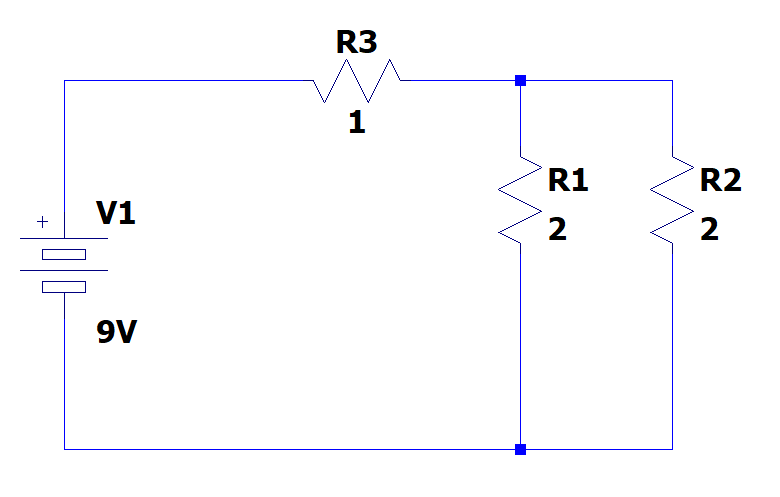
- 2\mathrm{\Omega }, 40.5 W
- 4\mathrm{\Omega }, 140 W
- 1\mathrm{\Omega }, 50 W
Solución:
Comencemos por calcular la resistencia equivalente del circuito vista desde la fuente. Para ello, debemos desconectar a la fuente de 9V y aplicar resistencias en serie y paralelo hasta encontrar una única resistencia que represente al circuito.
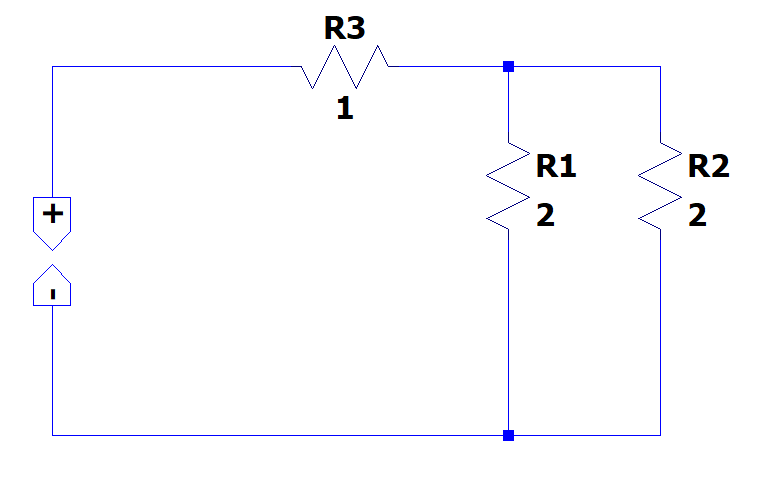
Resolvemos el paralelo entre {R}_{1} y {R}_{2} .
{R}_{1}//{R}_{2}=\frac{{R}_{1}{R}_{2}}{{R}_{1}+{R}_{2}}=\frac{\left(2\right)\left(2\right)}{2+2}=1 \mathrm{\Omega }
Ahora el circuito queda como:
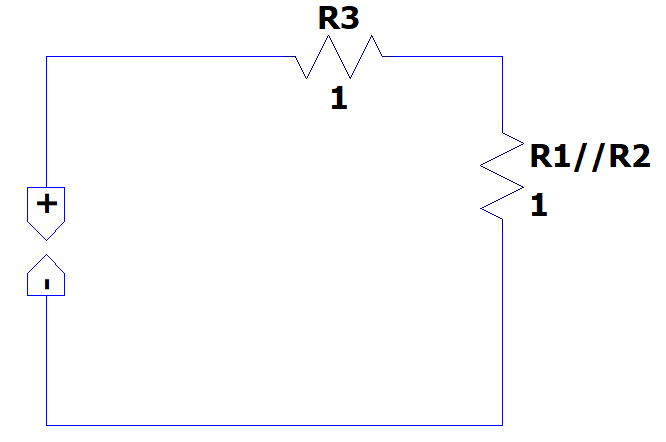
Finalmente, hacemos la serie entre {R}_{3} y {R}_{1}//{R}_{2} .
{R}_{\mathrm{3,2},1}=1 \mathrm{\Omega }+1 \mathrm{\Omega }=2 \mathrm{\Omega }
La potencia total consumida por el circuito, es la disipada por esta resistencia equivalente. La potencia en una resistencia se determina como:
P=\frac{{V}^{2}}{R}
Sustituimos:
{P}_{total}=\frac{{\left(9 V\right)}^{2}}{2 \mathrm{\Omega }}=40.5 W
Concluimos indicando como respuesta correcta la opción a).
Reactivo 38
Calcule el módulo de la fuerza magnética que experimentan dos hilos conductores a través de los cuales pasa una corriente de 2 y 4 amperios. Considere que la distancia entre los conductores es de 1 cm, con una longitud de 30 cm.
Tome en cuenta el valor de la permeabilidad magnética del vacío como: {\mu }_{o}=4\mathrm{\pi }\times {10}^{-7}\mathrm{ }\mathrm{N}/{\mathrm{A}}^{2} .
- 4.8\times {10}^{-6} \mathrm{N}
- 48\times {10}^{-6} \mathrm{N}
- 480\times {10}^{-6} \mathrm{N}
Solución:
Cuando circula una corriente a través de un conductor, este irradia a su alrededor un campo magnético circular centrado en el alambre conductor.
De esta manera, si dos alambres conductores con una cierta corriente {I}_{1} e {I}_{2} respectivamente se posicionan uno al lado de otro, el campo magnético de uno va a interactuar con la corriente del otro produciendo una fuerza magnética y viceversa.
La ecuación para calcular el módulo de la fuerza magnética es:
{F}_{\mathrm{1,2}}=L\frac{{\mu }_{o}\cdot {I}_{1}\bullet {I}_{2}}{2\pi d}
Donde L es la longitud del alambre sobre el que se mide la fuerza y d es la distancia entre los conductores. Ya que ambos tienen la misma longitud, la magnitud de la fuerza será igual en ambos. Sustituimos los valores dados por el enunciado.
{F}_{\mathrm{1,2}}=\left(0.3 \mathrm{m}\right)\frac{\left(4\mathrm{\pi }\times {10}^{-7}\mathrm{ }\mathrm{N}/{\mathrm{A}}^{2}\right)\cdot \left(2 \mathrm{A}\right)\bullet \left(4 \mathrm{A}\right)}{2\pi \left(0.01 \mathrm{m}\right)}=48\times {10}^{-6} \mathrm{N}
Comparando con las opciones, determinamos que la respuesta correcta es la opción b).
Reactivo 39
Relacione el elemento de circuito con el fenómeno electromagnético en el que está basado.

- 1c, 2a, 3b
- 1b, 2c, 3a
- 1a, 2c, 3b
Solución:
Para encontrar la combinación correcta, analizaremos el principio de funcionamiento de los elementos de circuito en la columna izquierda para relacionarlo con el fenómeno electromagnético en la columna derecha.
Condensador.
Los condensadores eléctricos son dispositivos que permiten almacenar cargas de diferentes signos entre las superficies de dos placas conductoras separadas por una distancia muy pequeña, entre las que se establece un campo eléctrico que le permite almacenar energía.
Teniendo en cuenta esta definición indicamos que:
1a.
Resistencia.
La resistencia eléctrica corresponde a la oposición del paso de la corriente que ofrecen los materiales. Esta oposición está ínfimamente relacionada con la estructura atómica de los materiales y se mide a partir de su resistividad eléctrica. Cada material, en función de su composición química y estructural ofrece una resistividad diferente.
Teniendo en cuenta esta definición:
2c.
Inductor.
Si se enrrolla en forma de helicoide un alambre conductor y se hace circular una corriente a través de él, en su interior se produce un campo magnético mientras se encuentre presente la corriente.
Concluimos entonces que:
3b.
Uniendo todas las soluciones:
1a, 2c, 3b.
Comparando con las opciones, determinamos que la c) es la correcta.
Reactivo 40
La onda de la figura corresponde a una fotografía tomada al movimiento ondulatorio uniforme de una cuerda. Calcula la longitud de la onda si el eje horizontal se encuentra expresado en metros.
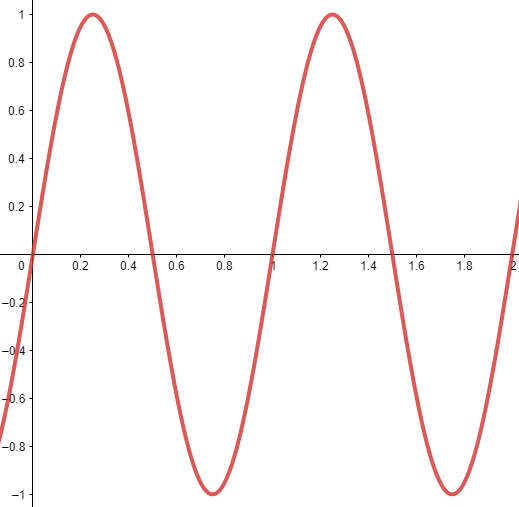
- 1 metro
- 2 metros
- 0.867 metros
Solución:
Por definición, la longitud de onda \lambda es la distancia que existe entre dos partículas consecutivas que se encuentran en fase, es decir, tienen la misma posición respecto a su segmento de vibración y la misma velocidad.
En resumen, para calcular la longitud de onda debemos medir la distancia entre dos puntos consecutivos a la misma altura. Para la onda de la imagen, los únicos puntos consecutivos y en fase distinguibles de medir se encuentran en 0 \mathrm{m} y en 1 \mathrm{m} , por tanto:
\lambda =1 \mathrm{m}-0\mathrm{ }\mathrm{m}=1 \mathrm{m}
Concluimos entonces que la longitud de onda es 1 metro y que la respuesta correcta es la a).


