Continuamos con la solución de la guía interactiva del EXANI II correspondiente a Pensamiento Matemático. En esta entrada vamos a desarrollar la segunda parte de la guía resuelta, correspondiente desde el reactivo 11 hasta el 20.

Recuerda resolverlos por tu cuenta antes de mirar la solución. Es necesario que desarrolles al máximo tu capacidad de análisis y comprensión lectora, antes de presentar el examen. ¡Iniciamos con la segunda parte!
Estructura del EXANI II
El Exani II de Ceneval consta de 168 reactivos, tiene una duración de 4 horas y media y se divide en diferentes módulos. Por eso, es importante familiarizarse con la prueba y conocer a detalle su estructura.
.2……En la siguiente tabla podrás ver los reactivos que lo componen.
| Área | Reactivos |
|---|---|
| Habilidades y conocimientos | |
| Pensamiento matemático | 30 |
| Comprensión lectora | 30 |
| Redacción indirecta | 30 |
| Módulos de conocimientos específicos | |
| Módulo 1 | 24 |
| Módulo 2 | 24 |
| Subtotal de reactivos | 138 |
| Diagnóstico | |
| Inglés | 30 |
| Total de reactivos | 168 |
Reactivos Resueltos
A continuación continuamos con la segunda parte de esta guía interactiva con reactivos resueltos de pensamiento matemático.
Reactivo 11
Considerando la siguiente gráfica, complete el enunciado para que represente una situación equilibradamente beneficiosa entre la oferta, la demanda y la tendencia de compra actual.

Al elaborar ___ productos, se tiene un costo de ___ por cada uno de ellos.
- 150, $200
- 300, $150
- 300, $250
Solución:
En un mercado financiero, el punto de equilibrio se encuentra cuando la demanda y la oferta por un producto coinciden con su tendencia de compra. A partir del gráfico, dicho punto de equilibrio se sitúa en 150 productos con precio unitario de 200 pesos.
Al elaborar 150 productos, se tiene un costo de 200 por cada uno de ellos.
La respuesta correcta es el inciso a). Teniendo en cuenta la definición dada al inicio, tanto el inciso b como el c, establecen puntos donde la demanda, oferta y tendencia de compra no se intersecan mutuamente.
Reactivo 12
Observe los siguientes segmentos y sus longitudes, algunas expresadas en términos de p.
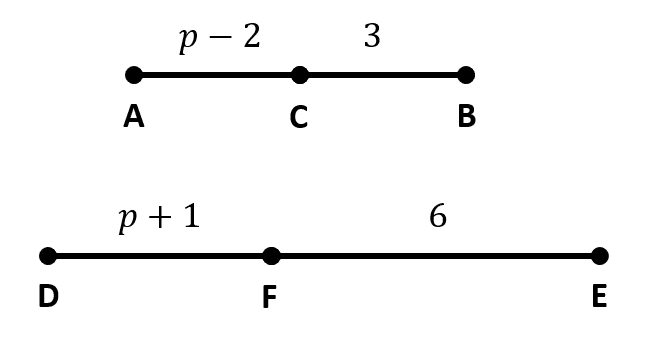
¿Para qué valor de p se cumple que \frac{AC}{CB}=\frac{DF}{FE} ?
- 3
- 4
- 5
Solución:
Para calcular el valor de p , es necesario sustituir la longitud de los segmentos en la igualdad de relaciones y despejar.
AC=p-2, CB=3, DF=p+1, FE=6
Sustituyendo se obtiene:
\frac{p-2}{3}=\frac{p+1}{6}
Despejando el valor de p se obtiene:
6\left(p-2\right)=3\left(p+1\right)\to 6p-12=3p+3
6p-3p=12+3
3p=15
p=5
El valor de p para que se cumpla la igualdad es de 5 unidades.
La respuesta correcta es el inciso c). El inciso a) no puede ser la respuesta correcta, porque en él se ha cometido un error al simplificar términos semejantes:
6p-3p=12+3\to 9p=15
En lugar de restar se ha sumado.
Por otra parte, en la opción b) se comete un error al momento de sustituir el valor de los segmentos CB y FE.
\frac{p-2}{6}=\frac{p+1}{3}
Reactivo 13
Un guardabosques observa la punta de un árbol a una distancia de 10.0 m. Al hacer esto se forma un ángulo de elevación de 65° respecto a su línea de visión (línea punteada).
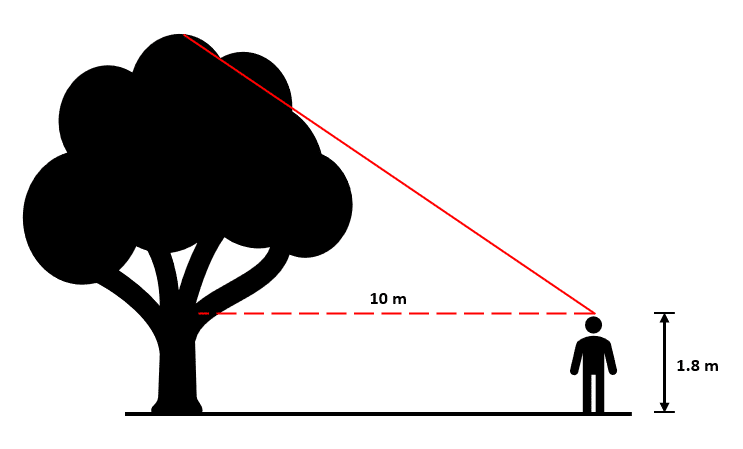
Considere que:
\begin{array}{c}\mathrm{sin}65°=0.90\\ \mathrm{cos}65°=0.42\\ \mathrm{tan}65°=2.1\end{array}¿Cuál es la altura del árbol?
- 21.0 m
- 22.8 m
- 25.6 m
Solución:
Para calcular la altura del árbol, primero se debe determinar la altura del triángulo y a este resultado sumarle la altura del guardabosques.
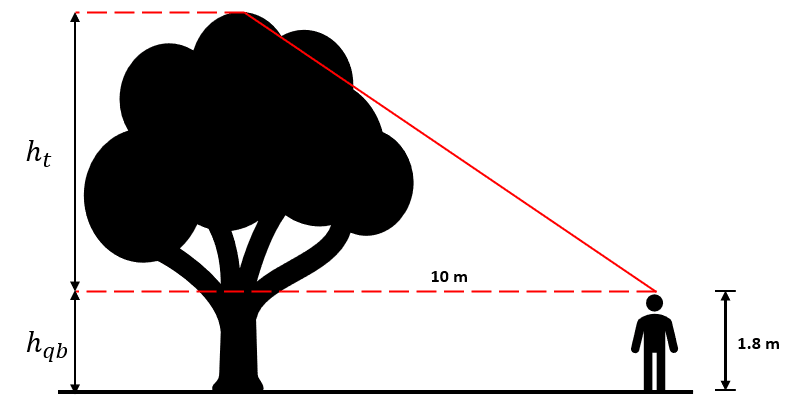
{h}_{a}={h}_{t}+{h}_{gb}
La altura del triángulo se obtiene mediante trigonometría, aplicando la tangente del ángulo de elevación.

\mathrm{tan}65=\frac{{h}_{t}}{10}\to {h}_{t}=10\mathrm{tan}65°
Sustituyendo el valor de la tangente de 65°:
{h}_{t}=10\left(2.1\right)=21 \mathrm{m}
Finalmente:
{h}_{a}=21+1.8=22.8 \mathrm{m}
La respuesta correcta es el inciso b). En el caso del inciso a) se identifica correctamente que debe calcular la longitud del cateto opuesto al ángulo que se tiene como dato y emplea la razón tan 65°. De esta forma calcula la longitud del cateto, pero olvida sumar la altura del guardabosques.
En el inciso c), ha empleado de forma incorrecta la razón trigonométrica cos 65°, debido a que confunde al cateto opuesto al ángulo con la hipotenusa del triángulo.
\mathrm{cos}65°=\frac{10}{H}\to H=\frac{10}{\mathrm{cos}65°}
Luego, le suma a este resultado la altura del guardabosques.
Reactivo 14
Complete la oración con el valor faltante.
Un árbol frutal crece en promedio _______ por año. Si el árbol mide 6.3 m, significa que actualmente tiene 10.5 años.
- 0.60 cm
- 1.66 cm
- 0.60 m
Solución:
Este problema se puede resolver mediante dos enfoques: utilizando razones y proporciones o mediante una regla de tres. El primer camino es el más rápido. Iniciamos calculando la razón de crecimiento en metros por año del árbol frutal:
\frac{6.3}{10.5}=0.6\frac{\mathrm{m}}{\mathrm{a}\mathrm{ñ}\mathrm{o}}
Esta razón nos dice que el árbol crece, en promedio, 0.6 metros por cada año.
La respuesta correcta es el inciso c). Si seleccionas como correcta la opción a), probablemente hayas tenido un error con las unidades para expresar el resultado, en lugar de metros has utilizado centímetros.
Por otra parte, el error en el inciso b) consta en realizar la división de forma incorrecta. En lugar de dividir metros sobre años, has dividido años sobre metros. Esta razón realmente establece que cada 1.66 años, el árbol crece 1 metro.
Reactivo 15
La siguiente gráfica representa un sistema de 3 ecuaciones de 2 variables.
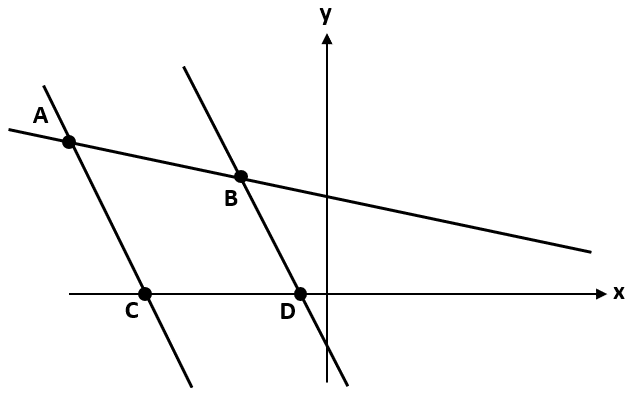
¿Cuál es la solución del sistema?
- Los puntos C y D son solución
- Los puntos A y B son solución
- No tiene solución
Solución:
La solución de todo sistema de ecuaciones, desde el punto de vista gráfico, es un punto por el que pasan todas las rectas que conforman el sistema.
En el gráfico se muestran tres rectas, las cuales representan 3 ecuaciones de 2 incógnitas, pero ninguno de los 4 puntos indicados sobre el gráfico pertenece simultáneamente a las 3 rectas.
Es decir, el sistema de 3 ecuaciones con 2 incógnitas no tiene solución. La respuesta correcta es el inciso c).
El inciso a) señala los puntos de corte con el eje x de las rectas paralelas, mientras que el inciso b) indica los puntos de intersección entre una de las rectas con las otras 2. Ninguno de los puntos mencionados en dichos incisos es solución del sistema.
Reactivo 16
Identifique la inecuación que describe el siguiente fenómeno.
De acuerdo con la Ley Federal del Trabajo, una persona debe laborar como máximo 42 horas semanales en horario nocturno; es decir, a lo sumo 7.5 horas diarias para cumplir con esta jornada.
- x = 7.5
- x ≥ 7.5
- x ≤ 7.5
Solución:
Este problema se resume en transformar una relación matemática expresada en lenguaje natural a lenguaje algebraico.
Nuestra variable son las horas diarias de trabajo, que denotaremos como x . En la frase: a lo sumo 7.5 horas diarias, se establece una relación de menor o igual que entre x y el número 7.5. Lo anterior se expresa matemáticamente como:
x\le 7.5
La respuesta correcta es el inciso c). Tanto en el inciso a) como en el b) se reconoce que la cantidad de comparación es 7.5, pero la relación es incorrecta.
En la primera se establece que la jornada es estrictamente igual a 7.5 horas y en la segunda que debe ser igual o mayor que 7.5, relaciones que no corresponden con el argumento “a lo mucho” en el enunciado.
Reactivo 17
Si \mathrm{sec}\alpha =\frac{5}{4} , calcule \mathrm{tan}\alpha .
- \frac{4}{5}
- \frac{4}{3}
- \frac{3}{4}
Solución:
En este caso, vamos a utilizar un triángulo rectángulo para encontrar el valor de la tangente del ángulo, recordando que:
\mathrm{sec}\alpha =\frac{\mathrm{H}\mathrm{i}\mathrm{p}\mathrm{o}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{u}\mathrm{s}\mathrm{a}}{\mathrm{C}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{t}\mathrm{o}\mathrm{ }\mathrm{a}\mathrm{d}\mathrm{y}\mathrm{a}\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{e}}
\mathrm{tan}\alpha =\frac{\mathrm{C}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{t}\mathrm{o}\mathrm{ }\mathrm{o}\mathrm{p}\mathrm{u}\mathrm{e}\mathrm{s}\mathrm{t}\mathrm{o}}{\mathrm{C}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{t}\mathrm{o}\mathrm{ }\mathrm{a}\mathrm{d}\mathrm{y}\mathrm{a}\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{e}}
A partir de la secante se obtiene:
\frac{\mathrm{H}\mathrm{i}\mathrm{p}\mathrm{o}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{u}\mathrm{s}\mathrm{a}}{\mathrm{C}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{t}\mathrm{o}\mathrm{ }\mathrm{a}\mathrm{d}\mathrm{y}\mathrm{a}\mathrm{c}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{e}}=\frac{5}{4}\to H=5, CA=4
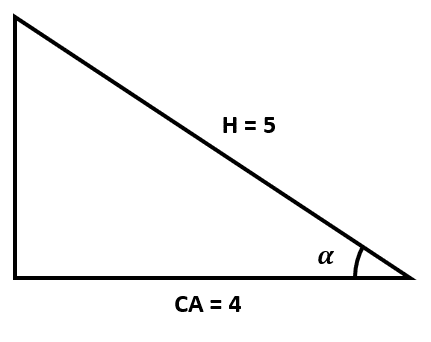
El cateto opuesto se calcula aplicando Pitágoras.
{H}^{2}=C{A}^{2}+C{O}^{2}\to CO=\sqrt{{5}^{2}-{4}^{2}}
CO=\sqrt{25-16}=\sqrt{9}=3
Finalmente:
\mathrm{tan}\alpha =\frac{3}{4}
La respuesta correcta es el inciso c). En el caso de haber seleccionado la a), probablemente hayas creído que la tangente es igual al inverso de la secante, pero en realidad, el inverso de la secante es igual al coseno.
\mathrm{cos}\alpha =\frac{1}{\mathrm{sec}\alpha }
En el inciso b), se calcula de forma correcta el cateto opuesto, pero los datos se sustituyen al revés. Acá obtienes el valor de la cotangente, no de la tangente.
Reactivo 18
¿Qué ruta es la correcta para llegar del punto A al punto B? Para el conteo tome como referencia sólo las cuadras del lado derecho del viajante.

- Caminar 3 cuadras hacia el sur, 5 cuadras hacia el oeste, 1 cuadra hacia el norte, 1 cuadra hacia el oeste y 1 cuadra hacia el norte
- Avanzar 2 cuadras hacia el sur, 2 cuadras hacia el oeste, 2 cuadras hacia el sur, 3 cuadras hacia el oeste y 2 cuadras hacia el norte
- Recorrer 1 cuadra hacia el norte, 1 cuadra hacia el oeste, 1 cuadra hacia el sur, 5 cuadras hacia el oeste y 1 cuadra hacia el sur
Solución:
En este caso, es necesario seguir las indicaciones de cada inciso para comprobar si con la ruta se puede ir desde el punto A hasta el B.
Camino a.
Caminar 3 cuadras hacia el sur.
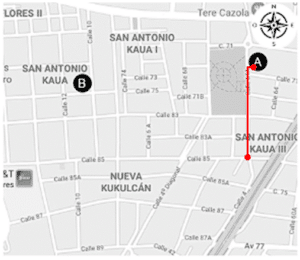
5 cuadras hacia el oeste.
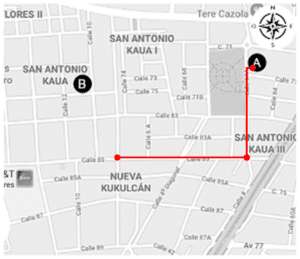
1 cuadra hacia el norte.
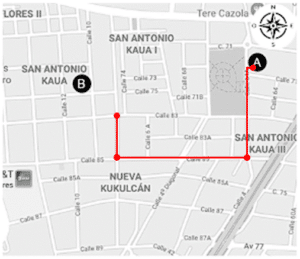
1 cuadra hacia el oeste.
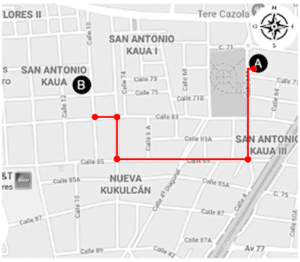
1 cuadra hacia el norte.
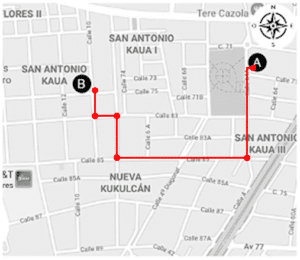
Luego de recorrer el camino del inciso a), hemos llegado al punto B, por lo tanto, la respuesta correcta es la opción a). Los recorridos descritos en los otros dos incisos no llevan hacia el punto B.
Camino b.
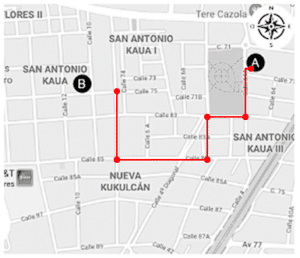
Camino C.

Reactivo 19
¿Cuál es la solución de la ecuación 4q – r = 12?
- Una posible solución es q = 1, r = -8
- No tiene solución
- La única solución es q = 1, r = -8
Solución:
La ecuación indicada por el enunciado: 4q-r=12 posee dos variables, por lo tanto, gráficamente corresponde con una línea recta; ecuación que posee infinitas soluciones, porque una recta está formada por infinitos puntos.
Teniendo en cuenta lo anterior, se descarta el inciso b) y el c), porque uno establece que no hay solución y otro que solo posee uno. Ambas aseveraciones contrastan con lo antes mencionado. Por lo tanto, la respuesta correcta es el inciso a).
Se comprueba sustituyendo los valores de q y r :
4\left(1\right)-\left(-8\right)=12
4+8=12
12=12
Reactivo 20
Una escuela organiza una selección de fútbol. Para elegir a la última integrante se considera el número de goles de 2 estudiantes, en los 5 últimos partidos.
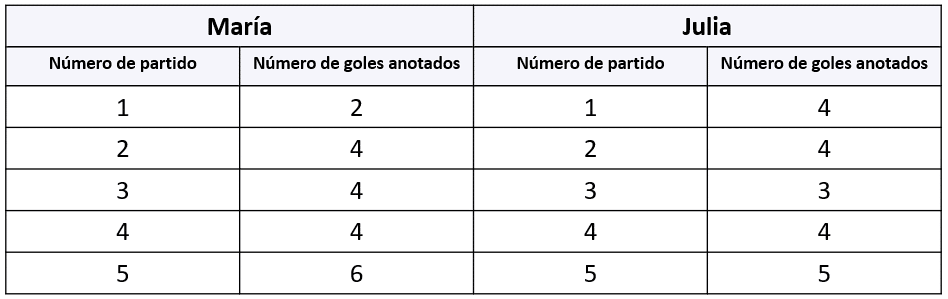
De acuerdo con la tabla, se observa que ambas tienen un promedio de 4 goles, pero el entrenador quiere que su desempeño en el partido no se aleje mucho de dicho promedio. Para elegir a la última integrante del equipo, el entrenador debe considerar a…
- María, ya que sus datos tienen el doble de dispersión que los de Julia, por lo que tiene el doble de rendimiento
- Julia, ya que la dispersión de su número de goles es menor que la de María
- otras candidatas, ya que la dispersión de los datos de María y Julia es menor que su media
Solución:
Para calcular la dispersión asociada a un conjunto de datos, tenemos tres parámetros estadísticos: rango, varianza y la desviación típica. Las dos últimas, permiten conocer el grado de desviación que tienen los datos respecto de la media.
Debido a que calcular la varianza es equivalente a calcular la desviación típica, este será el parámetro que emplearemos para medir la dispersión de los datos.
{s}^{2}=\frac{\sum {f}_{i}{\left({x}_{i}-\stackrel{-}{x}\right)}^{2}}{N}
Nos apoyamos en tablas para calcular {f}_{i}\cdot {\left({x}_{i}-\stackrel{-}{x}\right)}^{2} . Debido a que hay números de goles repetidos, en lugar de escribirlos varias veces, se les asigna una frecuencia {f}_{i} correspondiente al número de veces que aparecen en la tabla.
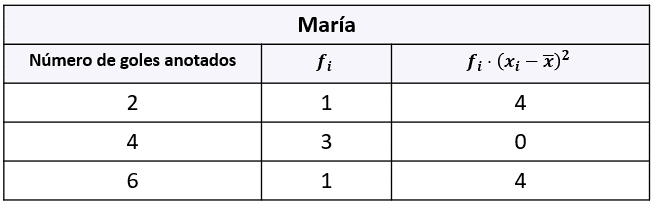
Cálculos para los datos de María.
{s}_{M}^{2}=\frac{4+0+4}{5}=\frac{8}{5}=1.6
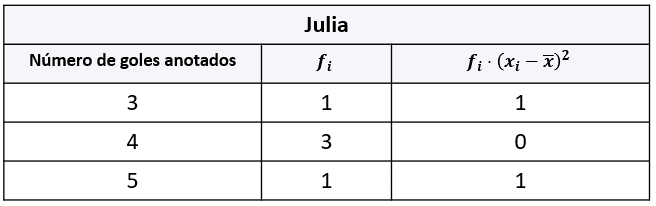
Cálculos para los datos de Julia.
{s}_{J}^{2}=\frac{1+0+1}{5}=\frac{2}{5}=0.4
Con estos resultados, se concluye que los registros de Julia tienen menor desviación que los registros de María. Teniendo esto en cuenta, la respuesta correcta es la del inciso b).
Si seleccionaste como respuesta correcta la opción a), probablemente hayas asociado la dispersión de los datos de María es del doble de Julia, confundiendo el concepto de desviación con el de rendimiento.
Por otro lado, el inciso c) considera que el valor de la dispersión es directamente proporcional al desempeño de las jugadoras, cuando realmente es al revés. Cuanto menor sea la dispersión respecto de la media, mejor es el desempeño.


