Llegamos a la última parte de la guía interactiva del EXANI II resuelta, correspondiente a Probabilidad y estadística desde el reactivo 13 hasta el 24.
Conviértete en un crack para tu examen de admisión con el resto de materiales para EXANI II. Recuerda medir el tiempo que tardas en resolver las guías e intenta mejorarlos con los trucos que te dejamos a continuación.
Curso Exani II 2024
Reactivo 13
Calcule el valor de x en la tabla de frecuencias, donde N = 44.
- 0.02
- 0.09
- 0.18
Solución:
La frecuencia relativa se calcula como el cociente entre la frecuencia absoluta de la clase y el total de elementos. La frecuencia absoluta de la clase es 4.
{f}_{r}=\frac{4}{44}=\frac{1}{11}=0.09
La respuesta correcta es el inciso b). En el inciso a) se calcula la frecuencia relativa como \frac{1}{44} , no se toma en cuenta la frecuencia absoluta de la clase. En el inciso c) se calcula la frecuencia relativa dividiendo respecto a la frecuencia absoluta de equipamiento Estándar: \frac{4}{22} .
Reactivo 14
Se lanzan 2 dados sin importar el orden y se registran sus caras. El evento A consiste en obtener un número par de la suma de estas, mientras que el B en lograr un número menor que 10 de la suma de sus caras.
¿Cuál es la intersección de los 2 eventos?
- {(1, 1), (2, 2), (3, 3), (4, 4)}
- {(1, 1), (1, 3), (1, 5), (2, 2), (2, 4), (2, 6), (3, 1), (3, 3), (3, 5), (4, 2), (4, 4), (5, 1), (5, 3), (6, 2)}
- {(1, 1), (1, 3), (1, 5), (2, 2), (2, 4), (2, 6), (3, 3), (3, 5), (4, 4)}
Solución:
El enunciado nos pide realizar la intersección de los conjuntos A y B. Primero debemos obtener los elementos de los conjuntos, teniendo en cuenta que no importa el orden. Es decir, si seleccionamos \left(1, 3\right) ya no es necesario seleccionar \left(3, 1\right) porque es la misma combinación.
Evento A: obtener un número par de la suma de estas.
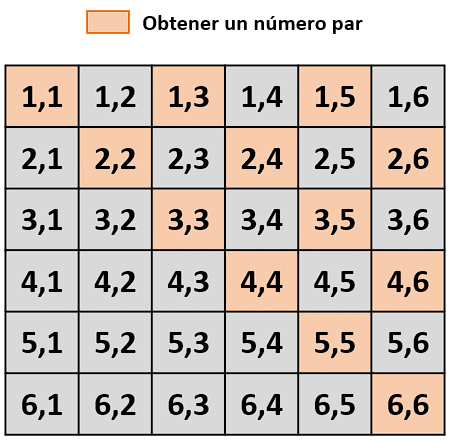
Evento B: en lograr un número menor que 10 de la suma de sus caras.
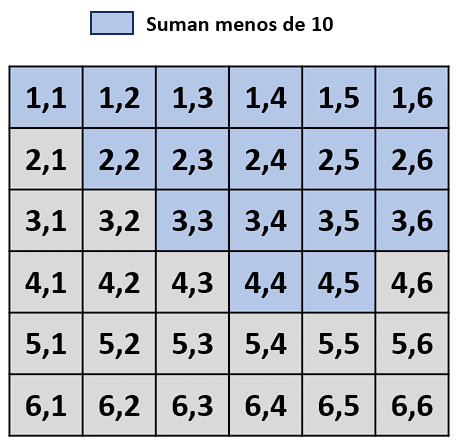
La intersección de los conjuntos es:
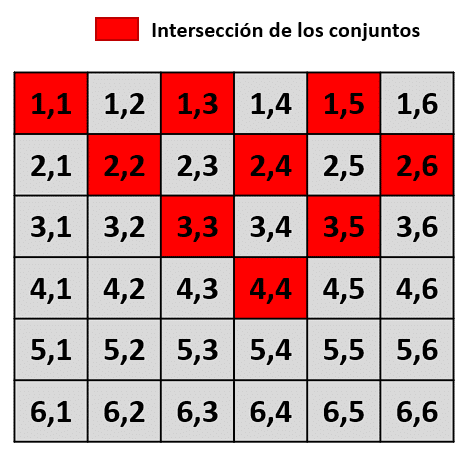
Finalmente:
A\cap B=\left\{\left(1,\mathrm{ }1\right),\mathrm{ }\left(1,\mathrm{ }3\right),\mathrm{ }\left(1,\mathrm{ }5\right),\mathrm{ }\left(2,\mathrm{ }2\right),\mathrm{ }\left(2,\mathrm{ }4\right),\mathrm{ }\left(2,\mathrm{ }6\right),\mathrm{ }\left(3,\mathrm{ }3\right),\mathrm{ }\left(3,\mathrm{ }5\right),\mathrm{ }\left(4,\mathrm{ }4\right)\right\}
La respuesta correcta es el inciso c). En la opción a) solo se toman las ocasiones donde los resultados son iguales, mientras que en la b) se olvida que no importa el orden, considerando las parejas conmutadas.
Reactivo 15
En un laboratorio se tiene en observación un conjunto de plantas que se estima presenta una extraña característica genética con probabilidad de 0.7. Para realizar un análisis se eligen 5 plantas al azar y se define la variable aleatoria X, la cual indica el número de plantas que presentan la extraña característica.
Determine la probabilidad de que en la elección la planta 3 presente dicha característica.
Considere para su cálculo la fórmula de la función de distribución:
P\left(X=k\right)=\frac{n!}{\left(n-k\right)!\cdot k!}\left({p}^{k}\right){\left(1-p\right)}^{n-k}
- 0.132
- 0.308
- 0.343
Solución:
La fórmula asignada por el enunciado responde a la de una distribución binomial, en la que identificamos a n=5 el total de plantas seleccionadas, k=3 las plantas que podrían tener la característica y p=0.7 la probabilidad de que aparezca la característica genética.
Sustituyendo los valores en la fórmula de la distribución binomial nos queda:
P\left(X=5\right)=\frac{5!}{\left(5-3\right)!\cdot 3!}\left({0.7}^{3}\right){\left(1-0.7\right)}^{5-3}
P\left(X=5\right)=\left(10\right)\left(0.343\right)\left(0.09\right)=0.3087
La probabilidad de que 3 de las 5 plantas seleccionadas presenten la característica es del 0.308. La respuesta correcta es el inciso b). En el inciso a) se comete un error al confundir las probabilidades de éxito y fracaso: p=0.3 y 1-p=0.7 , dando como resultado P\left(X=3\right)=0.132 .
Por otro lado, en el inciso c) se aplica de forma directa la ley multiplicativa sin tener en cuenta las posibles combinaciones {C}_{3}^{5} , ni la probabilidad de fracaso. Haciendo esto se obtiene: \left(0.7\right)\left(3\right)=0.343 .
Reactivo 16
Identifique el tipo de frecuencia presentado en la columna z.
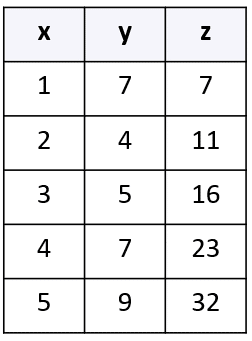
- Absoluta
- Relativa
- Acumulada
Solución:
Para llegar a una conclusión, debemos analizar las tres columnas de la tabla, teniendo en cuenta los conceptos de frecuencia absoluta y acumulada. En la primera columna se presentan los datos estudiados, por lo que allí no se indica ninguna frecuencia.
Por otro lado, en la columna y se indica la frecuencia absoluta mientras que en la z la frecuencia absoluta acumulada porque el valor de la fila 2 columna z se obtiene al sumar 7+4 . Esto se verifica con todas las filas.
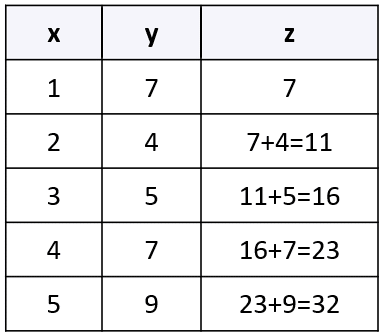
Concluimos entonces que la columna z es la frecuencia absoluta acumulada. La respuesta correcta es el inciso c).
Como ya mencionamos, la columna z no puede ser la frecuencia absoluta, porque ésta corresponde con la y y tampoco puede ser la frecuencia relativa, porque esta es un valor decimal menor que 1. Por estas razones, ni a) o b) pueden ser correctas.
Reactivo 17
El evento A se define como obtener una esfera azul de una urna, y P(A) = 0.30, mientras que el evento B se determina como lograr sol en el lanzamiento de una moneda cargada, y P(B) = 0.45. Si estos eventos son independientes, calcule P(A ∩ B).
- 0
- 0.135
- 0.75
Solución:
Debido a que los eventos son independientes, la probabilidad de que ambos ocurran al mismo tiempo se calcula con la regla del producto.
P\left(A\cap B\right)=P\left(A\right)\cdot P\left(B\right)
Sustituimos:
P\left(A\cap B\right)=\left(0.3\right)\left(0.45\right)=0.135
La respuesta correcta es el inciso b). En el inciso b) se ha deducido que: debido a que los sucesos son independientes, la intersección de los mismos es vacía A\cap B=\varnothing por lo tanto: P\left(A\cap B\right)=0 .
En el inciso c) se aplica la fórmula para calcular la probabilidad de la intersección de sucesos no ajenos. El error en este caso, ocurre al no distinguir el caso de uso para la ecuación:
P\left(A\cap B\right)=P\left(A\right)+P\left(B\right)-P\left(A\cup B\right)
Reactivo 18
Calcule el percentil 30 de los datos.
0.8, 1.2, 1.5, 0.7, 0.5, 0.6, 0.9, 1.0, 1.3, 0.1
Considere: {P}_{k}=\frac{n\cdot k}{100} .
- 0.6
- 1.2
- 1.5
Solución:
Para calcular el percentil 30 de un grupo de datos no agrupados, debemos ordenarlos de forma ascendente.
0.1, 0.5, 0.6, 0.7, 0.8, 0.9, 1, 1.2, 1.3, 1.5
Ahora, empleamos la fórmula suministrada por el enunciado para calcular la posición del percentil requerido. Donde n es el total de datos y k el percentil en cuestión.
{P}_{30}=\frac{10}{100}\left(30\right)=3
El percentil 30 se encuentra en la posición 3, es decir: {P}_{30}=0.6 .
La respuesta correcta es el inciso a). En el inciso b) se comete el error de ordenar de forma descendente a los datos. Por otro lado, en el inciso c) ni siquiera se ordenan los datos.
Reactivo 19
Un experimento tipo Bernoulli tiene asociada una probabilidad de éxito p = 0.83, cuando n = 1.
¿Cuál es la varianza de x?
- 14
- 17
- 66
Solución:
En la distribución de Bernoulli, la varianza se calcula como:
{\sigma }^{2}=p\left(1-p\right)
Sustituimos la probabilidad de éxito en la ecuación:
{\sigma }^{2}=\left(0.83\right)\left(1-0.83\right)=0.141
La respuesta correcta es el inciso a). En los incisos b) y c) se hace un mal uso de la ecuación para calcular la varianza de un experimento que obedece la distribución de Bernoulli.
Reactivo 20
¿Con qué tipo de distribución se determina la probabilidad de obtener x número de aciertos al contestar al azar un examen de opción múltiple con n número de preguntas?
- Bernoulli
- Normal
- Binomial
Solución:
Analizaremos cada una de las distribuciones, para luego concluir cuál permitiría modelar el experimento aleatorio.
La distribución de Bernoulli se utiliza en experimentos aleatorios discretos con dos posibles resultados: éxito y fracaso, obedeciendo la siguiente función de probabilidad:
f\left(x\right)={p}^{x}{\left(1-p\right)}^{1-x}
Donde x es la cantidad de éxitos en el experimento. Esta distribución no se ajusta a los planteado por el enunciado, porque solo contempla dos posibles resultados y el examen tiene n preguntas.
La distribución Normal se utiliza para experimentos aleatorios con variables continuas, pero nuestro experimento es discreto y de 4 posibles resultados. No es útil la distribución normal en este caso.
Por descarte, sabemos que la respuesta correcta es el inciso c). La distribución Binomial es el caso general de la distribución de Bernoulli, ya que aplica sobre experimentos con posibilidad de éxito y fracaso, pero el cuál puede llevarse a cabo n cantidad de veces. La expresión de dicha distribución es:
f\left(x\right)=\left(\begin{array}{c}n\\ x\end{array}\right){p}^{x}{\left(1-p\right)}^{n-x}
La inclusión del combinatorio de n con x , introduce todas repeticiones del experimento. Concluimos que la respuesta correcta es el inciso c).
Reactivo 21
En una heladería se realiza una encuesta para conocer la satisfacción de sus clientes sobre los productos que ofrece. Una de las preguntas es acerca del sabor del helado y las posibles respuestas son «muy bueno», «bueno», «regular» y «malo».
¿Qué tipo de variable estadística corresponde a las posibles respuestas?
- Ordinal
- Nominal
- Discreta
Solución:
Las variables probabilísticas se clasifican en dos grupos: continuas y discretas, donde estas últimas pueden ser ordinales o nominales.
Las variables nominales son aquellas que implican cierto orden o jerarquía, por ejemplo: muy malo, malo, bueno y muy bueno. Por otro lado, las variables nominales no establecen una relación de orden o jerarquía, como el color de ojos o el color de piel.
Teniendo en cuenta todo lo anterior, la respuesta correcta es el inciso a). No puede ser nominal por lo ya explicado, mientras que una variable discreta es una variable cualitativa que solo tiene un conjunto finito de valores.
Reactivo 22
¿Cuál es la probabilidad de acertar la combinación de un candado cuya contraseña es 0613 si los dígitos que puede tener son del 0 al 6 y no se permiten repeticiones?
- \frac{1}{2401}
- \frac{1}{840}
- \frac{1}{24}
Solución:
Primero, debemos calcular las posibles contraseñas aplicando la fórmula de permutaciones sin repetición:
{P}_{n}^{m}=\frac{m!}{\left(m-n\right)!}
Sustituimos m=7 y n=4 .
{P}_{4}^{7}=\frac{7!}{\left(7-4\right)!}=\frac{7!}{3!}=840
Finalmente, la probabilidad se obtiene mediante la fórmula clásica.
P\left(x=0613\right)=\frac{1}{840}
La respuesta correcta es el inciso b). En la opción a) se han calculado las permutaciones considerando que se permiten las repeticiones. Por otro lado, en el inciso c) se ha utilizado un método incorrecto para el cálculo del total de resultados.
Reactivo 23
Una propiedad de la curva de la distribución normal es que…
- su moda coincide con su media y su mediana
- sirve para conocer el número de éxitos en cierto número de intentos
- es útil en eventos impredecibles
Solución:
Vamos a analizar cada una de las propiedades enunciadas, para encontrar aquella que sea correcta.
Su moda coindice con su media y su mediana.
Gracias a que la distribución normal es simétrica, la moda y la media corresponden con el mismo valor. Recordemos que la moda es el valor con mayor probabilidad de salir, mientras que la mediana es el valor que divide en dos partes iguales al conjunto.
En la distribución normal, la mediana es el valor con mayor probabilidad de ser obtenido.
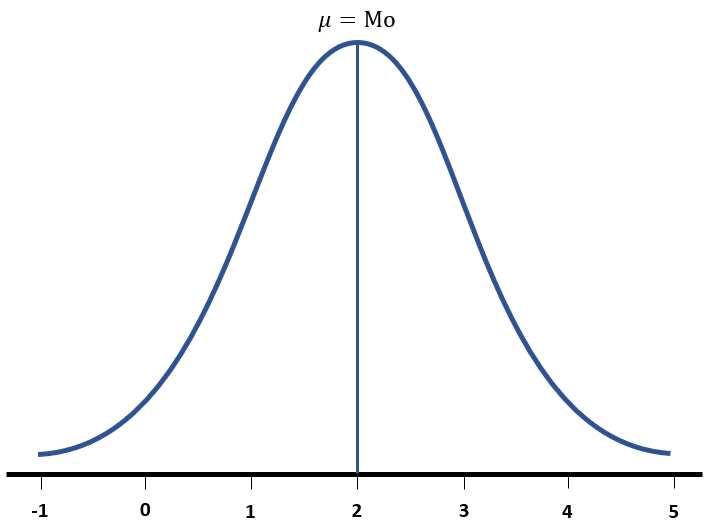
La respuesta correcta es el inciso a). El inciso b) describe una situación que se puede modelar con la distribución Binomial, mientras que la c) puede modelarse con la distribución de Poisson que posee un sesgo hacia la izquierda, útil para eventos impredecibles.
Reactivo 24
La distribución del ingreso diario por familia de una pequeña ciudad se representa por una variable aleatoria x, con una media de 500 y una desviación estándar de 75.
¿Cuál es el valor z estandarizado correspondiente a x = 610?
- 0.696
- 1.070
- 1.466
Solución:
Al indicarnos el valor de z , sabemos que debemos trabajar con la distribución normal estandarizada, es decir, en base a la desviación típica. La fórmula que relaciona a z con el resto de variables es:
z=\frac{x-\mu }{\sigma }
Sustituimos los respectivos valores de x , \mu y \sigma .
z=\frac{610-500}{75}=1.466
El valor estandarizado para x=610 es de z=1.466 .
La respuesta correcta es el inciso c). Tanto en el inciso a) como en el b) se confunden los parámetros en la fórmula. Primero se asigna x=500 , \mu =75 y \sigma =610 , mientras que en la segunda se confunde la media con la desviación estándar.
