¡Hola aspirante! Este es el primero de una serie de tutoriales en los que vamos a resolver juntos 50 ejercicios de Probabilidad y Estadística del módulo 14 de la prueba de conocimientos específicos del nuevo examen de admisión Exani II de Ceneval.

En resumen, estos son los elementos más importantes que debes considerar con respecto al Exani II:
- Desarrollo: Ceneval
- Examen de admisión: Exani II
- Reactivos: 168
- Tipo: Opción múltiple
- Duración: 4 horas y media
- Modalidades: Presencial, en línea y desde casa.
Con estos reactivos y las recomendaciones que te dejo más abajo, podrás emular las condiciones del examen real para el módulo de Probabilidad y Estadística. Recuerda resolverlos por tu cuenta antes de mirar la solución, tu nota es proporcional al esfuerzo que inviertas durante la preparación.
Estructura del Exani II
Para el periodo 2022-2023, la prueba de ingreso EXANI II de CENEVAL ha sufrido varios cambios y el principal son las dos grandes partes que la componen: conocimientos generales, denominada oficialmente como habilidades y conocimientos y conocimientos específicos que varía según la carrera a la que deseas ingresar.
Conocimientos generales cuenta con una extensión total 90 reactivos, de los cuales 30 son de pensamiento matemático y otros 60 de español, divididos en partes iguales entre comprensión lectora y redacción indirecta.
Conoce la estructura de la guía Exani II y del examen de ingreso
| Área | Reactivos |
|---|---|
| Habilidades y conocimientos | |
| Pensamiento matemático | 30 |
| Comprensión lectora | 30 |
| Redacción indirecta | 30 |
| Módulos de conocimientos específicos | |
| Módulo 1 | 24 |
| Módulo 2 | 24 |
| Subtotal de reactivos | 138 |
| Diagnóstico | |
| Inglés | 30 |
| Total de reactivos | 168 |
Estos son los 15 módulos de conocimientos específicos
| 1. Administración | 9. Física |
| 2. Aritmética | 10. Historia |
| 3. Biología | 11. Literatura |
| 4. Cálculo diferencial e integral | 12. Matemáticas financieras |
| 5. Ciencias de la Salud | 13. Premedicina |
| 6. Derecho | 14. Probabilidad y estadística |
| 7. Economía | 15. Química |
| 8. Filosofía | 16. Psicología |
Temario de Probabilidad y Estadística
Aunque en la primera parte hay algunos reactivos de probabilidad y estadística, este módulo pretende comprobar más en profundidad las capacidades del estudiante en el manejo de estadística descriptiva y probabilidad clásica. A continuación, te dejo el desglose exacto de los temas que debes estudiar.
Estadística
- Fundamentos: población, muestra y tipos de variables
- Frecuencias y sus representaciones
- Medidas descriptivas
Probabilidad
- Elementos: conjuntos y eventos
- Cálculo de la probabilidad
- Distribuciones
Si te parecen muchos temas y aún no sabes de donde sacar la información, en la guía del EXANI II, hay una bibliografía recomendada para cada módulo. Estadística y probabilidad son asignaturas desafiantes, asegúrate de tener buen dominio de los conceptos y soltura con los ejercicios.
¿Cómo resolver el examen simulacro?
Los ejercicios del simulacro tienen la finalidad de ayudarte a: practicar los temas del examen real y mejorar el tiempo que tardas en resolverlos.
Las siguientes, son sugerencias para tener en cuenta mientras estudias con este simulacro.
- Resuelve completa cada parte por tu cuenta antes de mirar las respuestas
- Establece un tiempo no mayor a 20 minutos por cada 10 reactivos
- Analiza el procedimiento que has seguido para resolver los ejercicios y piensa en posibles alternativas que acorten el tiempo
- Asegúrate de tener unos minutos de sobra para comprobar tus respuestas
- Si un ejercicio parece complejo, ve al siguiente y resuélvelo de último. Lo mejor es mantener la concentración y no entrar en pánico
Reactivo 1
Relacione las actividades con la clase de estadística a la que pertenecen.

- 1ab y 2cd
- 1cd y 2ab
- 1bd y 2ac
Solución:
Para responder correctamente este reactivo, debemos recordar las definiciones asociadas a cada clase o rama de la estadística.
Estadística descriptiva.
Es la encargada de la recolección y análisis de los datos a partir de tablas o gráficas, para luego determinar cantidades que permitan expresar de forma numérica las características de una población en estudio.
Estadística inferencial.
Se encarga de elaborar planificaciones a futuro de una población a partir de emitir conclusiones de estudios hechos con anterioridad. También evalúa la fiabilidad de los resultados obtenidos a partir de una muestra de la población.
Considerando estas definiciones, queda claro cómo podemos relacionar la clase de estadística con las actividades enumeradas en la columna derecha. Pertenecen a la estadística descriptiva la b) y la d), mientras que a) y c) son actividades desempeñadas por la estadística inferencial.
Finalmente:
1bd y 2ac.
Comparando con las opciones, seleccionamos como correcta la c).
Reactivo 2
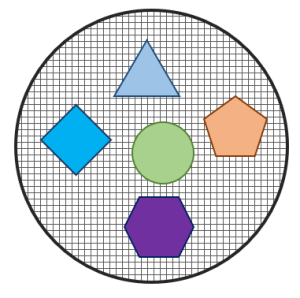
La figura muestra un conjunto de objetos clasificados como: polígonos regulares.
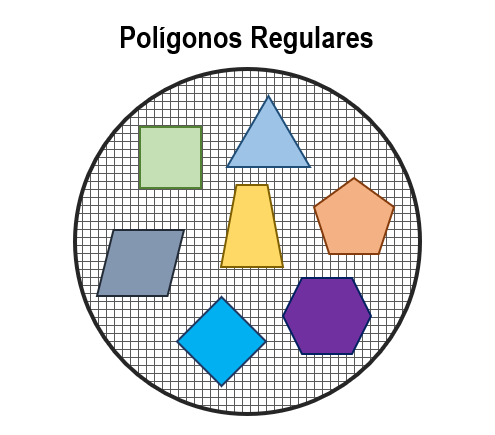
¿Cuál de las siguientes opciones es una muestra de la población?
Solución:
Para responder correctamente la pregunta, debemos recordar qué es la muestra de una población.
Muestra.
Es un subconjunto de la población total, a partir del cual se realizan los estudios estadísticos necesarios.
Considerando esta definición, podemos ir examinando cada una de las opciones para identificar cuál es la muestra de la población de polígonos regulares.
Primera imagen.
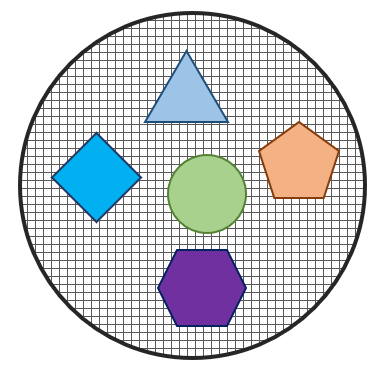
Esta no es una muestra de la población, porque en ella existe un elemento que no pertenece a los polígonos regulares: el círculo verde.
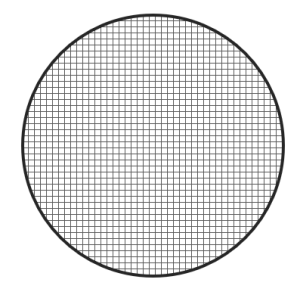
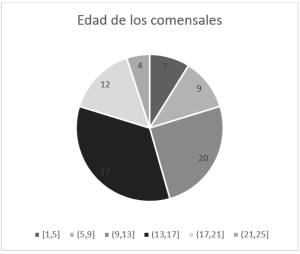
Segunda imagen.
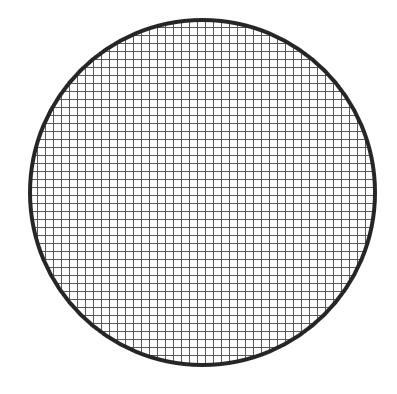
Esta directamente no posee ningún elemento, es propiamente el conjunto vacío y no es una muestra de la población en estudio.
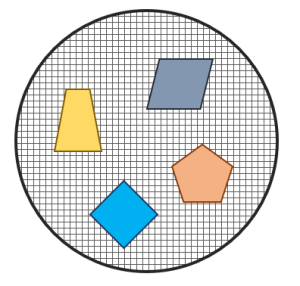
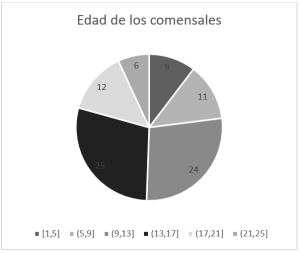
Tercera imagen.
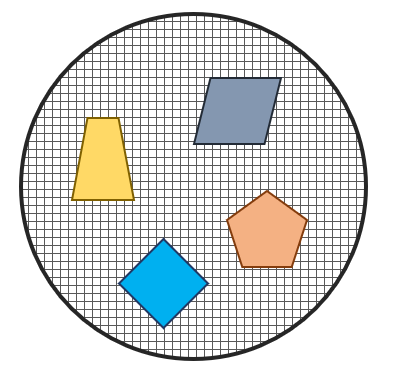
La tercera imagen muestra a un grupo de figuras compuesto por un paralelogramo, un trapecio, un rombo y un pentágono. Dichas figuras se encuentran todas en la población, por tanto, es una muestra de los polígonos regulares.
Concluimos seleccionando como respuesta correcta la opción c).
Reactivo 3
Un hotel implementó una encuesta corta en el check out para sus huéspedes, con la finalidad de analizar la experiencia que han tenido en sus instalaciones y mejorar, si hace falta. A continuación, se muestra un ejemplo de la encuesta.

- 1 y 2 cualitativas, 3 cuantitativa
- 1 cuantitativa, 2 y 3 cualitativas
- Todas cualitativas
Solución:
Recordemos lo que significa que una variable sea cualitativa o cuantitativa en el estudio estadístico.
Variable cualitativa.
Son todas aquellas características o rasgos de un sujeto de estudio que no se pueden expresar en cantidades numéricas, sino mediante palabras.
Variable cuantitativa.
Toda característica de un objeto de estudio que se puede medir y expresar de forma numérica.
Considerando estas definiciones, en la encuesta del hotel, para la primera pregunta se pide asociar un número a la experiencia con la atención, por tanto, es de tipo cuantitativa. Por otro lado, la segunda y tercera se expresan con adjetivos y con caritas que hacen referencia a adjetivos.
Indicamos entonces que la primera es cuantitativa, mientras que 2 y 3 son cualitativas. Comparando con las opciones, seleccionamos como correcta la b).
Reactivo 4
La estatura de un grupo de estudiantes que desean ingresar a la universidad se muestra en la siguiente lista de datos.
\mathrm{1,65}\mathrm{ }\mathrm{m};\mathrm{ }\mathrm{1,72}\mathrm{m};\mathrm{ }\mathrm{1,6}\mathrm{m};\mathrm{ }\mathrm{1,58}\mathrm{m};\mathrm{ }\mathrm{1,69}\mathrm{m};\mathrm{ }\mathrm{1,7}\mathrm{m}
¿El conjunto de datos es de tipo continuo o discreto? Justifique su respuesta.
- Discontinuo
- Discreto
- Continuo
Solución:
Los datos discretos, son aquellos que pueden tomar un conjunto de valores finitos como, por ejemplo: el número de hermanos, los integrantes de un equipo, las letras del abecedario, entre otras.
Por otra parte, los datos continuos son aquellos que pueden tomar cualquier valor en un determinado intervalo y se expresan como números decimales. Un dato continuo puede ser: el peso de un grupo de personas, la estatura, entre otros.
En base a todo lo anterior, las estaturas se expresan como números decimales en la unidad de medida: metros, no quedan dudas que corresponde a un dato de tipo continuo (además, lo enumeramos en la definición de dato continuo).
Seleccionamos como correcta la opción c).
Reactivo 5
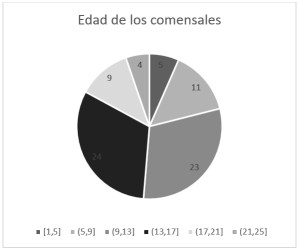
A partir de la siguiente distribución de frecuencias, seleccione la aseveración que sea correcta.
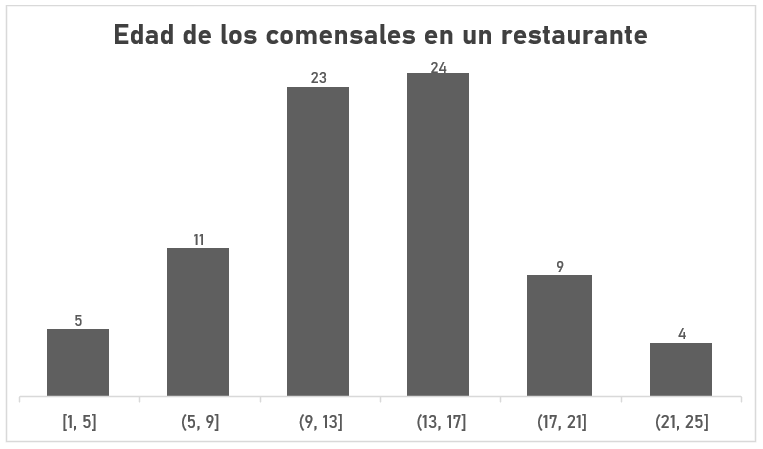
- La mayoría tiene entre 9 y 17 años
- La mayoría tiene más de 18 años
- Hay menos niños entre 1 y 5 años que adultos mayores a 21 años
Solución:
La gráfica del enunciado muestra un histograma de frecuencias correspondiente a las edades de los comensales en un restaurante, seguramente con la intención de definir el target principal del restaurante.
Se puede observar como las barras del centro tienen mayor amplitud que las barras de los extremos, juntas suman 47 individuos, mientras que las otras juntas 29. Esto pone en evidencia que la mayoría del público que acude al restaurante tiene entre 9 y 17 años.
Claramente, los adolescentes tienen una gran afinidad por el local. En base a esto y examinando las opciones del enunciado, concluimos que la respuesta correcta es la a).
Reactivo 6
La cantidad que cuantifica el número de veces que se manifiesta un evento o característica en una muestra o población recibe el nombre de:
- Muestra parcial
- Frecuencia absoluta
- Frecuencia relativa
Solución:
Luego de recolectar datos, extraer la muestra representativa de la población y tabular ordenadamente al subconjunto seleccionado, se procede a contar el número de veces que se presenta cada elemento o evento dentro de la muestra y se escribe en una columna a la derecha de los datos.
Los valores en cada casilla de esa columna reciben el nombre de frecuencia absoluta del evento en la tabla de datos. En esta línea de ideas, podemos indicar que la frase del enunciado define correctamente a la frecuencia absoluta.
Concluimos seleccionando como respuesta correcta la opción b).
Reactivo 7
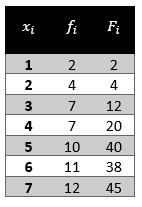
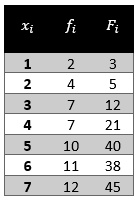
Rellene con el valor correcto las casillas en blanco de la siguiente tabla de frecuencias.
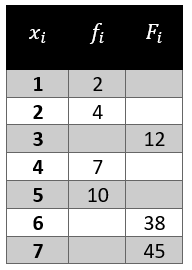
Solución:
En la tabla de frecuencias podemos identificar 3 columnas: la de datos, la de frecuencias absolutas {f}_{i} y la de frecuencia absoluta acumulada {F}_{i} . Para completar correctamente las casillas en blanco, debemos recordar que:
- La frecuencia absoluta corresponde a las veces que se presenta un evento
- La frecuencia absoluta acumulada corresponde a la suma de las frecuencias hasta el dato en cuestión
{F}_{i}={f}_{1}+{f}_{2}+{f}_{3}+\dots +{f}_{i}
La frecuencia acumulada para el dato 1 es {F}_{1}=2 y la frecuencia acumulada para el dato 2 es {F}_{2}=2+4=6 .
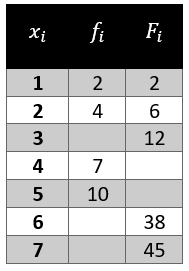
Para determinar la frecuencia absoluta del tercer dato aplicamos la siguiente ecuación.
{F}_{3}={f}_{1}+{f}_{2}+{f}_{3}\to {f}_{3}={F}_{3}-{f}_{1}-{f}_{2}={F}_{3}-{F}_{2}
{f}_{3}=12-4-2=6
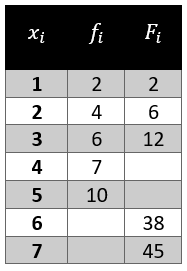
La frecuencia acumulada del dato 4 es {F}_{4}=12+7=19 , y para el dato 5 es {F}_{5}=19+10=29 .
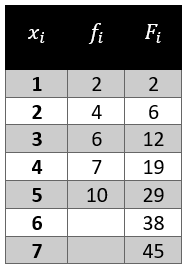
Para las frecuencias absolutas de 6 y 7 aplicamos:
{f}_{6}={F}_{6}-{F}_{5}=9
{f}_{7}={F}_{7}-{F}_{6}=7
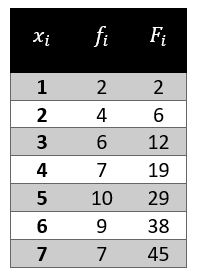
Comparando con las opciones, queda claro que la correcta es la b).
Reactivo 8
La prueba de ingreso diseñada por cierta Universidad, se ha constituido por un total de 100 preguntas, para el cual, participaron 80 aspirantes. La tabla de datos es la que se muestra a continuación.
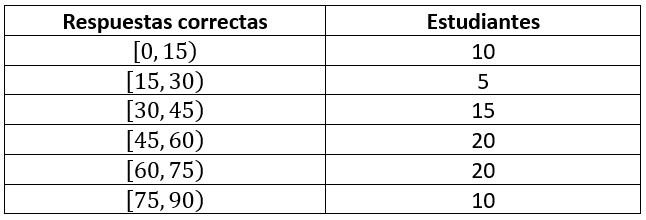
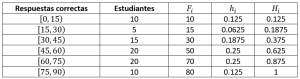
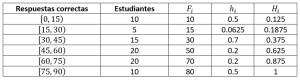
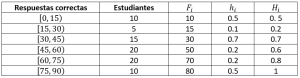
Agregue: frecuencia absoluta acumulada, frecuencia relativa y frecuencia relativa acumulada.
Solución:
Para agregar cada una de las columnas, iremos calculando la frecuencia correspondiente de cada dato y la integraremos a la tabla. Tengamos en cuenta, que la columna Estudiantes refleja la frecuencia absoluta de la población de estudio.
Frecuencia absoluta acumulada.
Se calcula como la suma de las frecuencias absolutas anteriores.
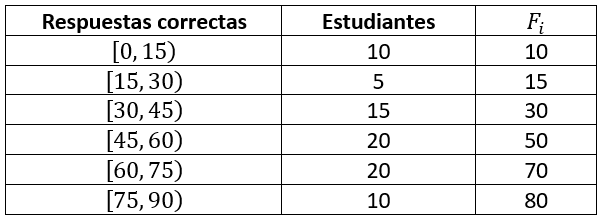
Frecuencia relativa.
Se calcula como el cociente entre la frecuencia absoluta del dato entre el número total de eventos, en este caso N=80 .
{h}_{i}=\frac{{f}_{i}}{N}
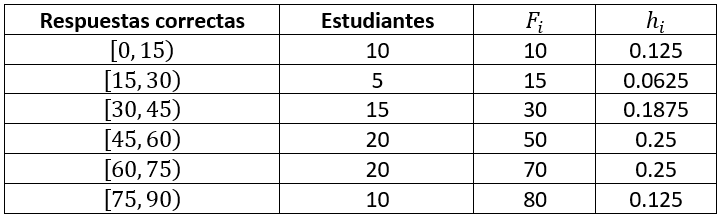
Frecuencia relativa acumulada.
Similar a la frecuencia relativa, pero en lugar de emplear la frecuencia absoluta, se hace con la frecuencia absoluta acumulada del dato.
{H}_{i}=\frac{{F}_{i}}{N}
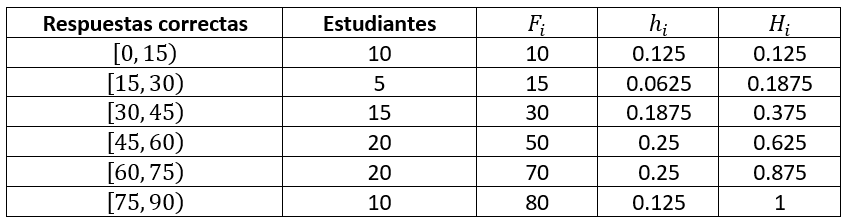
Comparando con las opciones del problema, concluimos que la respuesta correcta es la a).
Reactivo 9
A partir del siguiente histograma de frecuencias, seleccione el gráfico circular equivalente al mismo.

Solución:
Existen distintas formas de representar la tabla de frecuencias de un conjunto de datos estadísticos incluso, en muchos estudios es necesario pasar de una forma a otra para dar mejor visibilidad al gráfico.
Para convertir un gráfico de barras tipo histograma en uno circular, se toma la frecuencia absoluta o relativa expresada por las barras para representar cada una como porción de una circunferencia. El arco de dicha porción será más o menos grande en función de la frecuencia del dato en cuestión.
En esta línea de ideas, debemos seleccionar el gráfico circular cuyas porciones representan el valor de las barras en el histograma de frecuencias. Examinando las opciones, la que cumple con esto es la a).
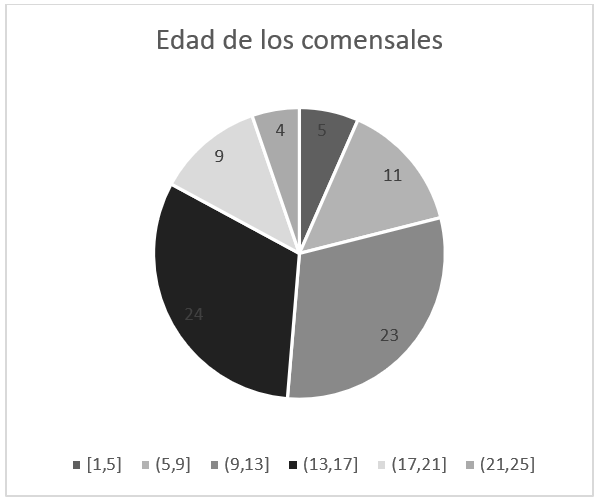
Respuesta correcta: a).
Reactivo 10
Una empresa ha recolectado las ventas en sus 155 sucursales alrededor del territorio mexicano durante el último trimestre. No es posible tomar una muestra, porque se necesitan datos lo más cercanos a la realidad para planificar estrategias de mercado.
Usted es el encargado de construir la tabla de frecuencias, ¿cuántos intervalos debe tener la tabla?
- 11
- 12.44
- 13
Solución:
En estadística, es muy común trabajar con volúmenes enormes de datos y una de las técnicas que emplean los estadistas para ahorrar tiempo y mejorar la eficiencia de sus análisis es separar a los datos por intervalos.
Cada intervalo representa los eventos correspondientes a los datos que entran en él. Existen distintos criterios para la selección del número de intervalos, pero el más utilizado es el de Norcliffe.
El número de intervalos de clase debe ser aproximadamente igual a la raíz cuadrada del número de datos.
\mathrm{N}\mathrm{I}\mathrm{C}\approx \sqrt{N}
Si el resultado es decimal, se escoge el entero superior inmediato. En este caso, si N=155 , el número de intervalos que se deben construir es:
\mathrm{N}\mathrm{I}\mathrm{C}\approx \sqrt{155}=12.44
Aproximamos al inmediato superior:
\mathrm{N}\mathrm{I}\mathrm{C}=13
La tabla de frecuencias se debe construir con 13 intervalos de clase.
Concluimos indicando como correcta la opción c).
Reactivo 11: Estadística descriptiva
Elija los enunciados que son propios del objeto de estudio de la estadística descriptiva.
- Contrastar la validez de una teoría por medio del análisis de regresión
- Investigar y aplicar los procedimientos correctos de recopilación, ordenamiento y análisis de datos
- Hacer pronóstico de series temporales a partir de datos previos conocidos
- Aplicar a grupos de datos diversas medidas de exploración, como las de tendencia central y de dispersión
- Comparar la distribución de grupos de datos de interés con distribuciones teóricas, como la normal, la t de Student y otras
- Estimar los valores de parámetros desconocidos de una población por medio de inferencias sobre una muestra conocida y calcular la probabilidad de que sean iguales
- 1, 2, 6
- 1, 3, 4
- 2, 4, 5
Solución:
Para encontrar la combinación correcta de los incisos, analizaremos lo que se expone en cada uno y concluimos si corresponde o no con alguno de los objetos de estudio de la estadística descriptiva.
- Contrastar la validez de una teoría por medio del análisis de regresión
El análisis por regresión es una técnica que se basa en estimar la relación entre un conjunto de variables respecto de otra, para describir el comportamiento de un modelo y realizar predicciones.
La estadística descriptiva basa su estudio en la recopilación, ordenamiento y presentación de datos, es una técnica para el análisis de los datos recolectados a partir de un objeto de estudio. No corresponde.
- Investigar y aplicar los procedimientos correctos de recopilación, ordenamiento y análisis de datos
Siguiendo con lo dicho en el inciso anterior, este punto describe de forma resumida el principal objeto de estudio de la estadística descriptiva. Si corresponde.
- Hacer pronóstico de series temporales a partir de datos previos conocidos
Las series temporales son una herramienta para validar estudios estadísticos, además de predecir la demanda futura. Sin dudas, no forman parte del objetivo que tiene la estadística descriptiva. No corresponde.
- Aplicar a grupos de datos diversas medidas de exploración, como las de tendencia central y de dispersión
Para la descripción de los datos recolectados, la estadística descriptiva emplea diferentes medidas numéricas de exploración, entre ellas: medidas de tendencia central (media, mediana y moda) o medidas de dispersión como la desviación estándar. Si corresponde.
- Comparar la distribución de grupos de datos de interés con distribuciones teóricas, como la normal, la t de Student y otras
Las distribuciones teóricas son funciones que asocian una probabilidad a cada evento del objeto de estudio y por tanto, son herramientas para el análisis cuantitativo de los datos recolectados. Si corresponde.
- Estimar los valores de parámetros desconocidos de una población por medio de inferencias sobre una muestra conocida y calcular la probabilidad de que sean iguales
En la estadística se manejan tres tipos de parámetros: de centralización, de localización y de dispersión, a partir de ellos se puede organizar la información recolectada.
Por otro lado, la inferencia de dichos parámetros a partir de la inducción y otras técnicas pertenece a la estadística inferencial, no a la estadística descriptiva. No corresponde.
Uniendo los resultados parciales de cada inciso, concluimos que 2, 4 y 5 pertenecen a las técnicas de estudio de la estadística descriptiva. Comparando con las opciones, escogemos como respuesta correcta a la opción c).
Reactivo 12: Pasos de un trabajo estadístico
Ordene las fases que comprende todo trabajo estadístico.
- Recolección de datos
- Presentación de los datos
- Plan de recopilación
- Recuento de los datos
- Crítica de los datos
- 1, 5, 3, 2, 4
- 2, 3, 1, 4, 5
- 3, 1, 5, 4, 2
Solución:
Un estudio estadístico se realiza sobre un objeto y a partir de él, se recolectan una serie de datos que son de interés para el estadista. Suponiendo que ya se conoce cuál será el objeto, los pasos para llevar a cabo el estudio estadístico son:
Plan de recopilación (3). Se define el instrumento para la recolección de los datos que mejor se adecua a las circunstancias del experimento. En este punto se establece: el tamaño de la muestra, el tipo de muestra y el instrumento en sí (encuesta, entrevista, cuestionario, etc.)
Recolección de datos (1). El grupo de estudio pasa a aplicar los métodos e instrumentos definidos en el Plan de recopilación.
Crítica de los datos (5). Para evitar que una mala planificación en las etapas anteriores pase a la cuantificación de la información, los datos deben interpretarse para determinar el nivel de precisión y exactitud.
Recuento de los datos (4). Una vez interpretada y validada la calidad de la información recolectada, la misma debe totalizar y organizarse para facilitar su posterior tratamiento.
Presentación de los datos (2). Por último, se recurre a instrumentos de representación gráfica para el conjunto de datos como tablas, mapas, gráficos de pastel, histogramas y otros.
En base al ordenamiento, concluimos: 3, 1, 5, 4, 2. Comparando con las opciones, escogemos como respuesta correcta a la c).
Reactivo 13: Estudio estadístico
A una compañía se ha solicitado una investigación que involucre experimentación, recolección de datos, organización, presentación, análisis, interpretación y que al final haga una toma de decisión. ¿Qué métodos incluyen todos los requerimientos solicitados para hacer dicho estudio?
- Estadísticos
- Probabilísticos
- De muestreo
Solución:
Todos los requerimientos que se hacen llegar a la compañía corresponden a las distintas etapas de un estudio estadístico, ya que se debe recolectar, analizar y presentar de forma ordenada un conjunto de datos provenientes de una investigación.
En base a esto, escogemos como respuesta correcta a la opción a).
Reactivo 14: Etapas de un estudio estadístico
¿Qué actividad de la estadística se refleja al comparar los resultados de dos grupos de mujeres, uno de 20 años y otro de 60, con una prueba para muestras independientes?
- Recolectar
- Organizar
- Analizar
Solución:
En este caso, el escenario planteado describe un análisis de los datos recolectados, ya que se compara una parte de la población con otra con el fin de emitir conclusiones.
Escogemos como respuesta correcta a la opción c).
Reactivo 15: Población y muestra
Son ejemplos de muestras, excepto:
- Todos los hombres adultos de raza negra
- Un grupo de enfermeras especialistas del área de urgencias de un hospital público
- Los 10 mejores cantantes de la última década
Solución:
Por definición, una muestra se refiere a un subconjunto de eventos o elementos que pertenecen a una población, es decir no se refiere al total sino a una parte de ellos.
El único inciso que no alude a un subconjunto es el a), ya que habla de TODOS los hombres adultos de raza negra y no una parte de ellos. En su lugar, el resto de incisos hacen referencia clara a un subconjunto de la población.
Concluimos entonces que la opción que no es una muestra es la a).
Reactivo 16: Definiciones básicas en estadística
Relacione los conceptos con su definición.

- 1a, 2c, 3b
- 1b, 2a, 3c
- 1b, 2c, 3a
Solución:
Para relacionar correctamente cada columna, describiremos de forma resumida el concepto de la izquierda para luego asignarle su correspondiente definición de la columna derecha.
Población: Es un conjunto finito o infinito que representa al total de eventos en un estudio. Esta descripción corresponde con el inciso b de la columna derecha, por tanto:
1b.
Censo: corresponde al conjunto de datos recolectados de la población o una parte de ella. Esta descripción concuerda con la enunciada en el inciso a, por tanto:
2a.
Muestra: subconjunto o parte de la población estadística. Corresponde con el inciso c, por tanto:
3c.
Uniendo todas las respuestas:
1b, 2a, 3c.
Comparando con las opciones, escogemos como correcta a la b).
Reactivo 17: Población finita
La población formada por todos los estudiantes de la escuela secundaria Simón Bolívar es:
- Infinita
- Representativa
- Finita
Solución:
Una población se considera finita si no es infinita o si el proceso de contabilizar tiene un fin y, en efecto la cantidad de estudiantes en la secundaria Simón Bolívar puede representarse por un número, por tanto: es una población finita.
Escogemos como respuesta correcta a la opción c).
Reactivo 18: Variables cualitativas y cuantitativas
¿Cuáles son ejemplos de variables cualitativas?
- Estatura y peso
- Estado civil y ocupación
- Número de autos y de alumnos
Solución:
Una variable es cualitativa si su valor o conjunto de valores no se puede representar de forma numérica. En este caso la estatura y el peso, el número de autos y de alumnos o el tiempo y la temperatura no son cualitativas, porque se representan mediante números.
Por otro lado, el estado civil y la ocupación son variables cualitativas porque sus valores expresan características descritas de forma no numérica. Concluimos que la respuesta correcta es la opción b).
Reactivo 19: Variables discretas y continuas
Elija las variables discretas.
- Tirar 2 dados y observar la suma obtenida
- Anotar el color del pelo de los transeúntes por una calle durante media hora
- Obtener la relación estatura-peso de 100 personas
- Registrar la velocidad a las Que pasan tos autos por un punto
- Preguntar a 100,000 personas por su preferencia electoral
- Calcular la relación ventas totales-empleo en una muestra de 100 empresas
- 1, 2, 5
- 1, 3, 6
- 2, 3, 4
Solución:
Una variable es discreta si no puede tomar valores intermedios entre dos datos consecutivos.
La suma del resultado de lanzar 2 dados (1), el color de cabello de los transeúntes (2) y la preferencia electoral de un grupo de personas (5), son ejemplos de variables discretas, ya que no existen valores intermedios.
En base al análisis, la combinación correcta es 1, 2, 5. Comparando con las opciones, la respuesta correcta sería la a).
Reactivo 20: Variables discretas y continuas
Son ejemplos de datos continuos, excepto:
- El peso de una persona
- Las materias inscritas en el semestre
- El costo de una comida
Solución:
Una variable que no es continua se denomina discreta y por ende, no puede tomar valores intermedios entre dos datos contiguos.
En base a lo anterior y examinando los incisos, las materias inscritas en el semestre es una variable no continua ya que no existe tal cosa como 5.4 materias inscritas (valor que se encuentra entre 5 y 6).
Concluimos entonces que la respuesta correcta es la opción b), todas son continuas excepto las materias inscritas en el semestre.
Reactivo 21: Variables estadísticas
¿En qué tipo de variables es imposible hacer mediciones?
- Aleatorias
- Cuantitativas
- Cualitativas
Solución:
Las variables cualitativas son aquellas que permiten describir un evento a partir de cualidades o características y no pueden realizarse medidas sobre ellas. En base a lo anterior, concluimos que la variable que es imposible de medir es la c) Cualitativas.
Reactivo 22: Variables dicotómicas
¿Cuál es el tipo de variable que solamente puede tomar valores como “si” o “no”?
- Continua
- Dicotómica
- Discreta
Solución:
Por definición, una variable dicotómica es aquella que solo puede tomar dos valores. Un ejemplo clásico son las variables lógicas, donde 0 implica falso y 1 cierto o verdadero. En conclusión, escogemos como respuesta correcta a la opción b) Dicotómica.
Reactivo 23: Tipos de variables estadísticas
De las siguientes, ¿cuáles son variables cuantitativas? Se pretende medir la diferencia que existe entre el bienestar laboral de los empleados operativos de una empresa y los mandos medios.
- Tiempo de laborar en la empresa
- Estado civil
- Nivel de escolaridad
- Ingreso mensual
- Coeficiente intelectual
- Tipo de religión
- Edad
- 1, 2, 3, 6
- 1, 4, 5, 7
- 2, 3, 4, 5
Solución:
Una variable cuantitativa es aquella que puede expresarse a través de cifras o cantidades numéricas. En base a lo anterior, escogemos como variables cuantitativas a:
1. Tiempo de laborar en la empresa
4. Ingreso mensual
5. Coeficiente intelectual
7. Edad
El estado civil, el nivel de escolaridad y el tipo de religión representan una característica o cualidad del individuo (en este caso, de los empleados) y no se expresan como cantidades numéricas.
En conclusión, los incisos correctos con 1, 4, 5, 7. Comparando con las opciones, la respuesta correcta es la b).
Reactivo 24: Tipos de variables estadísticas
El número de goles en un partido de fútbol es una variable…
- Continua
- Discreta
- Independiente
Solución:
Como hemos indicado en reactivos anteriores, una variable es discreta si no puede tomar valores entre dos datos consecutivos. Efectivamente, los goles en un partido de fútbol no pueden ser 1.5; o es 1 o 2 pero nunca un valor intermedio, por tanto: es una variable discreta.
Escogemos como respuesta correcta a la opción b).
Reactivo 25: Rango
¿Cuál es el valor del rango de los datos, si su media muestral es 19.2?
17, 20, 21, 18, 20
- 1.469
- 2.160
- 4.0
Solución:
En estadística, el rango es una medida que establece la diferencia entre los extremos de una población. Antes de proceder con el análisis, debemos ordenar en forma creciente a los datos:
17,18,20,20,21
Ahora, tomamos los extremos del conjunto de datos 17 y 21 para calcular el rango:
\text { rango }=21-17=4
Comparando este resultado con las opciones, escogemos como respuesta correcta a la c).
Reactivo 26: Parámetros estadísticos
¿Cuál de los siguientes conceptos es una medida de dispersión?
- Media
- Mediana
- Varianza
Solución:
Las medidas de dispersión son aquellas que cuantifican la diversidad de un conjunto de datos, es decir que tan diferentes, variables o dispersos son entre ellos. Existen diferentes medidas de dispersión, entre ellas se encuentran:
- La desviación estándar
- Varianza
- Coeficiente de variación
- Rango
En base a lo anterior y comparando con las opciones, escogemos como respuesta correcta a la c). Por otra parte, la media, mediana y moda son medidas de tendencia central.
Reactivo 27: Probabilidad de eventos independientes
Si se lanza un dado y después una moneda, ¿qué probabilidad hay de que caiga 1 en el dado y águila en la moneda?
- \frac{1}{6}
- \frac{1}{2}
- \frac{1}{12}
Solución:
Lanzar un dado y luego una moneda son eventos independientes. La probabilidad asociada a dos eventos no relacionados se calcula como:
P(D \cap M)=P(D) P(M)
Es igual al producto de las probabilidades individuales de cada evento. Otra forma de verlo, es que al lanzar un dado tenemos 6 posibles resultados (1, 2, 3, 4, 5 y 6) y para cada uno de ellos, al lanzar la moneda tenemos 2 posibles resultados (Águila o Sol).
La probabilidad del dado es:
P(D)=\frac{1}{6}
La probabilidad de la moneda es:
P(M)=\frac{1}{2}
Sustituyendo.
P(D \cap M)=\left(\frac{1}{6}\right)\left(\frac{1}{2}\right)=\frac{1}{12}
Comparando con las opciones, escogemos como respuesta correcta a la c.
Reactivo 28: Eventos mutuamente excluyentes
Seleccione los eventos que se clasifican como excluyentes.
- Que en el partido final de fútbol gane el equipo azul o el equipo rojo
- Que Lucía cargue el paraguas y llueva ese día por la tarde
- Al tirar un dado en 2 ocasiones se obtenga primero un 5 y después un 6
- Qué rumbo al trabajo, Efrén decida tomar el camino A o el camino B
- 1, 2
- 1, 4
- 2, 3
Solución:
Dos eventos se consideran excluyentes si y solo si, la probabilidad de que uno de ellos ocurra no está condicionada por la verificación del otro. En base a esto, pasamos a examinar lo enunciado en cada inciso.
- Que en el partido final de fútbol gane el equipo azul o el equipo rojo
Ambos eventos son excluyentes porque si gana el azul automáticamente pierde el rojo y viceversa.
- Que Lucía cargue el paraguas y llueva ese día por la tarde
Estos eventos no son excluyentes, porque el que Lucia tenga su paraguas no afecta de ninguna manera el que llueva ese día por la tarde.
- Al tirar un dado en 2 ocasiones se obtenga primero un 5 y después un 6
Los eventos no son excluyentes, porque la probabilidad de obtener un 5 en el primer intento no imposibilita obtener 6 en el segundo.
- Qué rumbo al trabajo, Efrén decida tomar el camino A o el camino B
Si Efrén escoge el camino A se anula automáticamente la posibilidad de que valla por el B.
Teniendo en cuenta el análisis en cada inciso, los eventos mutuamente excluyentes ocurren en 1 y 4. Comparando con las opciones, escogemos como respuesta correcta a la opción b).
Reactivo 29: Estadística
Rama de las Matemáticas que organiza, recopila y analiza datos para dar conclusiones y tomar decisiones razonables.
- Probabilidad
- Estadística
- Álgebra
Solución:
La estadística es la parte de las matemáticas que se ocupa de los métodos para obtener, organizar, representar e interpretar conjuntos de datos, frecuentemente muy numerosos.
Con lo anterior, respaldamos que la respuesta correcta es la opción b).
Reactivo 30: Principio multiplicativo
En una tienda automotriz, la lista de precios de los automóviles se organiza conforme al tipo de motor, suspensión y transmisión que tenga. Existen 8 tamaños de motor, 3 tipos de suspensión y 3 de transmisión. ¿Cuántos precios contiene la lista, según estas características?
- 9
- 8/24
- 72
Solución:
Cada uno de los parámetros de clasificación para dar precio a los automóviles puede verse como una “etapa”. Primero se establece el tamaño del motor (hay 8 posibles tamaños), luego el tipo de suspensión (3 posibles tipos) y por último la transmisión (3 posibilidades).
Por tanto, debemos aplicar el principio multiplicativo para calcular el número total de precios que se pueden construir en base a estos parámetros.
N^{\circ} \text { total }=8 \cdot 3 \cdot 3=72
Escogemos como respuesta correcta a la opción c).
Reactivo extra: Probabilidad clásica
Un grupo de amigos que van al cine tienen 4 opciones de películas y no saben cuál elegir, cada uno sugiere una propuesta para decidir a qué función entrar, ¿cuál propuesta representa el concepto de probabilidad clásica?
- Decidir con base en las críticas positivas de las reseñas
- Preguntar al vendedor de boletos cuál ha sido la más vista
- Escribir los nombres en papeles para elegir por tómbola
Solución:
La propuesta que describe un ejemplo básico de probabilidad clásica es la c). En él, cada película tiene la misma probabilidad de ser escogida P(p)=\frac{1}{4} . Concluimos que la respuesta correcta es la opción c).
Reactivo extra: Frecuencia
Elija las situaciones en que se emplea el enfoque frecuencial de probabilidad para tomar una decisión.
- En una carrera de caballos, un señor apuesta a que el número 5 será el ganador, partiendo de que en las últimas 10 carreras, este ha acumulado 7 carreras ganadas.
- La probabilidad de que una persona gane un volado cualquiera, es igual a 0.50, sin importar el número de veces que lance la moneda.
- Un señor compra un billete de lotería con terminación 7, basado en la observación de que en los últimos 20 sorteos, este número ha aparecido en 10 de las combinaciones ganadoras.
- Una persona compró un boleto para participar en la rifa de una televisión, la probabilidad de que gane esta rifa, compuesta por 100 números, es igual a 1 en 100.
- 1, 2
- 1, 3
- 2, 4
Solución:
En probabilidad y estadística, la frecuencia de un evento indica el número de veces que el mismo se ha manifestado. La frecuencia puede ser absoluta, relativa o acumulada.
Los incisos 1 y 3 describen, de forma explícita, decisiones tomadas en base a la ocurrencia previa de un evento o dicho de otra forma, basadas en su frecuencia absoluta. Concluimos entonces que la respuesta correcta es la b).