Guía Exani II: 30 Ejercicios de pensamiento matemático Parte II

En este tutorial vamos a resolver los reactivos del 11 al 21, correspondientes a la segunda parte de los ejercicios de Pensamiento Matemático del simulacro para el examen de ingreso EXANI.

Recuerda desarrollarlos por tu cuenta antes de mirar la solución. Este simulacro tiene la finalidad de acercarte a los ejercicios que saldrán en la prueba real, la única forma de lograr una buena calificación es a través de la práctica constante.

Ejercicios de Pensamiento Matemático

Continuamos con la segunda parte del simulacro de Pensamiento Matemático para EXANI. Una vez hayas resuelto los problemas, analiza el procedimiento que has seguido, identifica posibles fallas y puntos de mejora para acortar el tiempo.

Reactivo 11

¿Cuál es la probabilidad de obtener como suma el número 4 al lanzar dos dados?

1. \frac{1}{2}
2. \frac{1}{8}
3. \frac{1}{12}

Solución:

En este caso, debemos recordar la definición de probabilidad simple o directa, expresada a través de la definición de Laplace:

La probabilidad de ocurrencia de A como P\left(A\right) , es igual al cociente de los eventos favorables de A sobre el total de eventos.

P\left(A\right)=\frac{{N}_{A}}{N}

Para el lanzamiento de dos dados, el espacio muestral tiene un total de 36 posibles eventos, tal como se muestra en el siguiente gráfico.

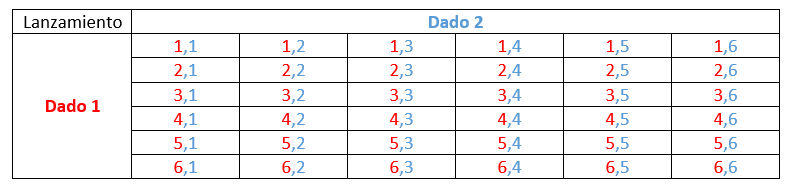
En él, podemos ver que solo 3 eventos hacen que ambos dados sumen 4: \left(3, 1\right) , \left(2, 2\right) y \left(1, 3\right) . Entonces:

{N}_{4}=3 y N=36

P\left(4\right)=\frac{3}{36}=\frac{1}{12}

Comparando con las opciones, concluimos que la respuesta correcta es la c).

Reactivo 12

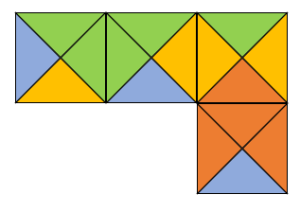
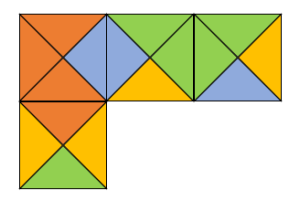
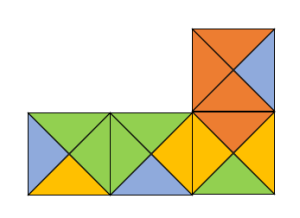
La figura muestra un conjunto de Azulejos de Wang. Son figuras compuestas por azulejos con bordes de colores. La regla para conectarlos, es que los bordes de dos azulejos sean del mismo color y para desplazarse solo se pueden mover hacia arriba, abajo y los lados; pero no admiten giros ni reflexiones.

Con los 4 azulejos de la figura, encuentra el mosaico correcto.

1. 
2. 
3. 

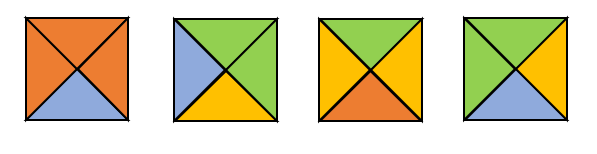
Solución:

Encontrar el mosaico correcto es sencillo si seguimos las reglas impuestas en el enunciado.

1. No se puede hacer reflexión de las piezas

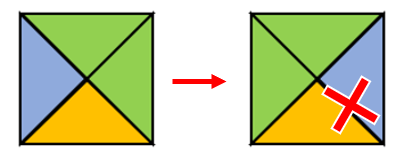
2. Tampoco se pueden rotar piezas

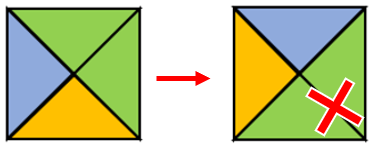
Para facilitar el desplazamiento, asignaremos un número a cada pieza.

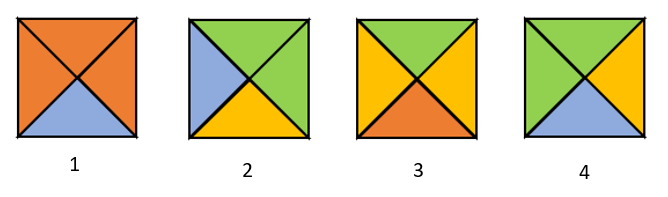
Podemos desplazar hacia abajo y luego a la derecha a la pieza 1 para conectarla a la parte inferior de la pieza 3.

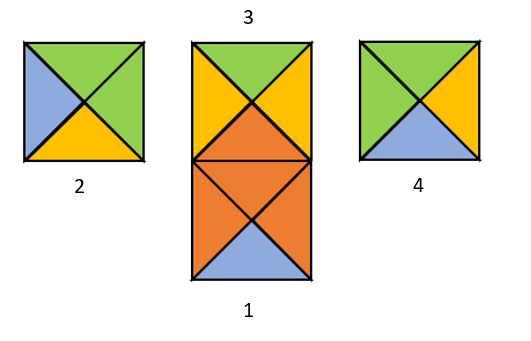
Ahora, se desplaza hacia arriba, luego hacia la izquierda y finalmente hacia abajo la pieza 4 para conectarla con la pieza 2 y 3.

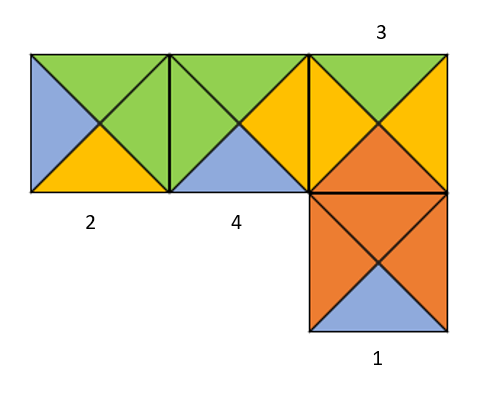
Sin más piezas que conectar, comparamos con las opciones e indicamos como correcta la a).

Reactivo 13

En una tienda, el dueño está liquidando peras, manzanas y papayas al 50% de su precio original. Además, por tratarse del viernes negro, el dueño decide darles a todos los productos un 25% de descuento. El precio original de las peras es de 5$, de las manzanas 12$ y de las papayas 8.5$.

¿Cuánto deberá pagar un cliente que lleva 2 kilos de peras, 3 de manzanas, 1 de papayas y un kilo de tortillas a 5$?

1. 22.5$
2. 32.8$
3. 24.2$

Solución:

Debido a que el cliente lleva productos que tienen el primer descuento del 50%, debemos aplicar al precio total de estos, dicho descuento. El monto bruto por los 2 kilos de peras, 3 de manzanas y 1 de papayas se calcula como la suma de los productos de los pesos y los precios por kilo.

\left(2kg*5\frac{\$}{kg}+3kg*12\frac{\$}{kg}+1kg*8.5\frac{\$}{kg}\right)*\left(1-{D}_{1}\right)=\left(54.5\$\right)*\left(1-0.5\right)

=27.25\$

Debido a que el dueño les da un descuento a todos los productos del 25%, debemos aplicarlo a la cuenta que lleva el cliente.

=27.25\$*\left(1-{D}_{2}\right)=27.25\$*\left(1-0.25\right)=20.44\$

Ahora, debemos sumar el kilo de tortillas a la cuenta y aplicarle el descuento del 25%.

=20.44\$+5\$*\left(1-0.25\right)=24.18\$

El cliente debe cancelar 24.18$ por los productos que se lleva.

Comparando con las opciones, la respuesta correcta es la c).

Reactivo 14

La conversión de metros a pies (ft) es: un metro equivale a 3.28 ft. Si un terreno mide 200 metros de ancho y 188 metros de largo, ¿Cuál es el área en pies cuadrados del terreno?

1. 3000000 ft
2. 123455 f{t}^{2}
3. 404516 f{t}^{2}

Solución:

Para calcular el área del terreno en pies, debemos transformar el largo y ancho del mismo a esta unidad, empleando el factor de conversión dado por el enunciado.

1 \mathrm{m}=3.28\mathrm{ }\mathrm{f}\mathrm{t}

Procedemos con las transformaciones.

200 \mathrm{m}\mathrm{*}\frac{3.28\mathrm{ }\mathrm{f}\mathrm{t}}{1 \mathrm{m}}=656 \mathrm{f}\mathrm{t}

188 \mathrm{m}\mathrm{*}\frac{3.28\mathrm{ }\mathrm{f}\mathrm{t}}{1 \mathrm{m}}=616.64 \mathrm{f}\mathrm{t}

Calculamos el área en pies como el producto de las longitudes transformadas.

{A}_{t}=\left(656 \mathrm{f}\mathrm{t}\right)\left(616.64 \mathrm{f}\mathrm{t}\right)=404515.84 {\mathrm{f}\mathrm{t}}^{2}

Comparando con las opciones, la respuesta correcta es la c).

Reactivo 15

Identifica los exponentes n y m que hacen equivalente a la expresión \frac{{b}^{3n}}{{\left({a}^{2}\right)}^{\frac{m}{2}}} con \frac{{\left({b}^{3}\right)}^{9}}{{a}^{4}} .

1. n=2, m=3
2. n=9, m=4
3. n=m=1

Solución:

En este caso, debemos aplicar correctamente las propiedades de los exponentes. Primero, simplifiquemos las potencias aplicando potencia de una potencia en ambas expresiones.

\frac{{b}^{3n}}{{\left({a}^{2}\right)}^{\frac{m}{2}}}=\frac{{\left({b}^{3}\right)}^{9}}{{a}^{4}}\to \frac{{b}^{3n}}{{a}^{2*\frac{m}{2}}}=\frac{{b}^{3*9}}{{a}^{4}}

\frac{{b}^{3n}}{{a}^{m}}=\frac{{b}^{27}}{{a}^{4}}

Para trabajar una ecuación de potencias, debe cumplirse que las bases sean iguales para igualar los exponentes y resolver la ecuación.

Las bases de los numeradores y denominadores son iguales respectivamente, por tanto, para que se cumpla la igualdad, los exponentes deben coincidir en el numerador y en el denominador.

3n=27\to n=9

m=4

Comprobamos fácilmente el resultado sustituyendo los valores de m y n .

\frac{{b}^{3\left(9\right)}}{{a}^{4}}=\frac{{b}^{27}}{{a}^{4}}

Concluimos que la respuesta correcta se encuentra en el inciso b).

Reactivo 16

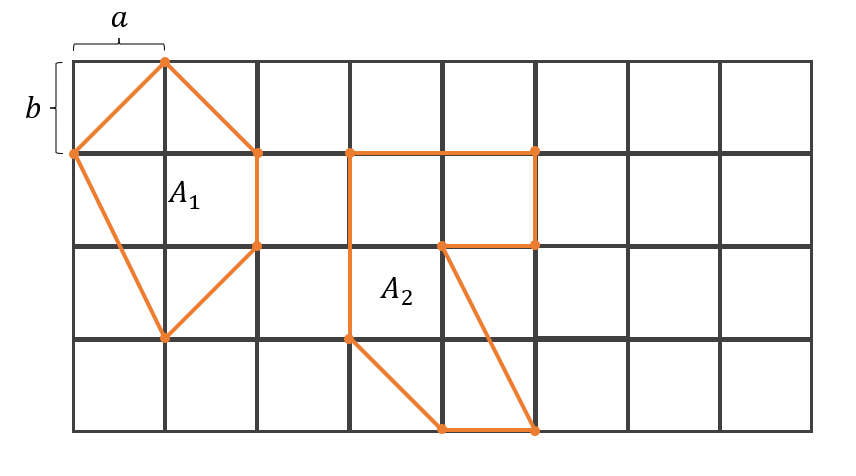
Calcula la longitud de a y b para que la suma de las áreas de las figuras 1 y 2 sea igual a 25 unidades cuadradas. Considera además que: a=\frac{b}{8} .

1. a=3, b=3
2. a=\frac{5}{8}, b=5
3. a=\frac{8}{5}, b=3.12

Solución:

Desde el principio, el problema deja claro que debemos llegar a un sistema de ecuaciones para encontrar el valor de a y b . En principio, debemos estimar el área de las figuras, sumarlas e igualarlas a 25.

Área de figura {A}_{1}

{A}_{1} está compuesta por 3 triángulos y un cuadrado.

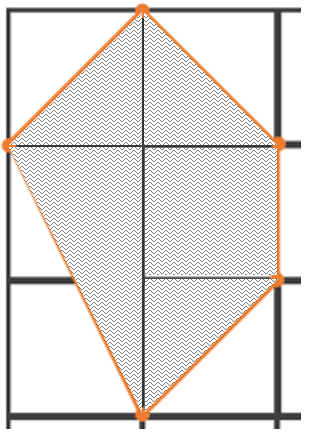
{A}_{1}=\frac{ab}{2}+\frac{ab}{2}+\frac{ab}{2}+\frac{a2b}{2}+ab=\frac{3}{2}ab+2ab=\frac{7}{2}ab

Área de figura {A}_{2} .

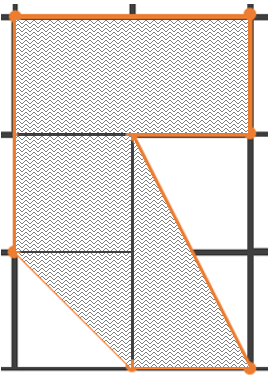
{A}_{2}=2ab+ab+\frac{ab}{2}+\frac{a2b}{2}=4ab+\frac{ab}{2}=\frac{9}{2}ab

Procedemos a sumar las áreas.

25=\frac{7}{2}ab+\frac{9}{2}ab=8ab

\therefore 8ab=25

Ahora, tenemos dos ecuaciones con dos incógnitas:

a=\frac{b}{8}; 8ab=25

Aplicamos el método de sustitución.

8\frac{b}{8}b=25\to {b}^{2}=25

\therefore b=5

a=\frac{5}{8}

Finalmente:

a=\frac{5}{8}, b=5

Comparando con las opciones, seleccionamos como correcta la b).

Reactivo 17

Encuentra la suma de los polinomios:

P\left(x\right)+G\left(x\right)

Considerando que:

P\left(x\right)={x}^{2}-3x+2

G\left(x\right)=-2{x}^{2}+{x}^{3}-3

1. {x}^{3}-2
2. -{x}^{3}+{x}^{2}+3x+1
3. {x}^{3}-{x}^{2}-3x-1

Solución:

Para resolver este problema, debemos aplicar suma de polinomios entre las funciones P\left(x\right) y G\left(x\right) .

P\left(x\right)+G\left(x\right)={x}^{2}-3x+2+\left(-2{x}^{2}+{x}^{3}-3\right)

Eliminamos el paréntesis y sumamos o restamos los términos semejantes.

P\left(x\right)+G\left(x\right)={x}^{2}-3x+2-2{x}^{2}+{x}^{3}-3

P\left(x\right)+G\left(x\right)={x}^{3}+{x}^{2}-2{x}^{2}-3x+2-3={x}^{3}-{x}^{2}-3x-1

\therefore P\left(x\right)+G\left(x\right)={x}^{3}-{x}^{2}-3x-1

Comparando con las opciones, la respuesta correcta es la c).

Reactivo 18

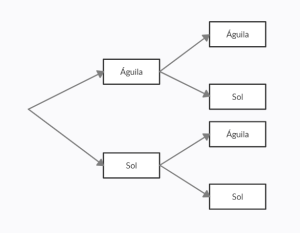
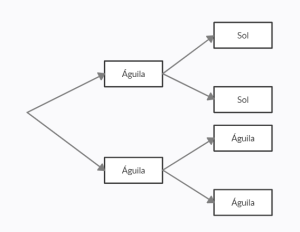
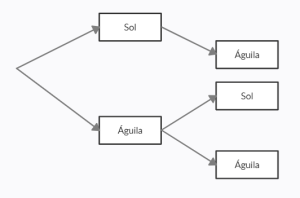
Realiza el diagrama de árbol asociado al experimento aleatorio de lanzar una moneda al aire dos veces.

1. 
2. 
3. 

Solución:

Para realizar el diagrama de árbol de este experimento aleatorio, debemos encontrar el espacio muestral del mismo emulando lo que sucedería al llevarlo a cabo. Empecemos por el primer lanzamiento, los posibles resultados son Sol o Águila.

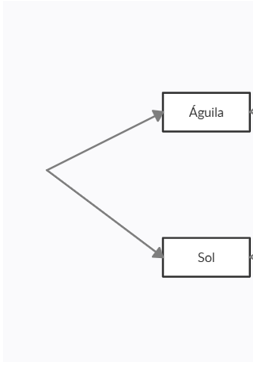
Ahora, estando en cualquiera de los resultados, si volvemos a lanzar la moneda las posibilidades vuelven a ser Sol o Águila. Representado en el diagrama de árbol quedaría:

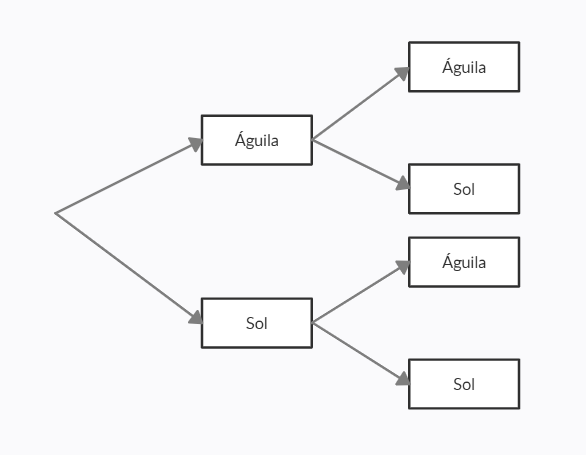
Comparando con las opciones, la respuesta correcta es la a).

Reactivo 19

Un sistema de ecuaciones compatible ______, es aquel que posee __________.

1. Determinado – una única solución
2. Indeterminado – una única solución
3. Parcialmente determinado – infinitas soluciones

Solución:

Para completar correctamente la frase, debemos recordar la teoría básica sobre la clasificación de sistema de ecuaciones lineales, específicamente, la clasificación en cuanto al número de soluciones que puede llegar a tener.

Un sistema de ecuaciones lineales es compatible de dos maneras:

1. Determinado, si posee un conjunto finito de soluciones
2. Indeterminado, si posee un número infinito de soluciones

Teniendo en cuenta esto y observando las opciones dadas por el problema, la que completa correctamente a la frase es la a).

Un sistema de ecuaciones compatible determinado, es aquel que posee una única solución.

Respuesta correcta: a).

Reactivo 20

Al realizar determinado experimento aleatorio, se obtiene que la probabilidad del evento A es P\left(A\right)=\frac{1}{2} y la probabilidad del evento B es P\left(B\right)=\frac{1}{3} . Además, un estudio posterior demostró que la probabilidad P\left(A\cup B\right)=\frac{1}{4} . Si ambos eventos son compatibles, ¿Cuál es la probabilidad de P\left(\stackrel{-}{A\cap B}\right) ?

1. 3/12
2. 5/12
3. 9/15

Solución:

Comencemos por recordar que la ecuación para calcular la probabilidad conjunta de eventos compatibles es:

P\left(A\cup B\right)=P\left(A\right)+P\left(B\right)-P\left(A\cap B\right)

De aquí despejamos P\left(A\cap B\right) .

P\left(A\cap B\right)=P\left(A\right)+P\left(B\right)-P\left(A\cup B\right)

Sustituimos.

P\left(A\cap B\right)=\frac{1}{2}+\frac{1}{3}-\frac{1}{4}=\frac{7}{12}

Pero el enunciado solicita la probabilidad del opuesto de A\cap B , es decir, la probabilidad de \stackrel{-}{A\cap B} . Para ello, empleamos la propiedad del suceso contrario:

P\left(\stackrel{-}{A\cap B}\right)=1-P\left(A\cap B\right)

Sustituimos.

P\left(\stackrel{-}{A\cap B}\right)=1-\frac{7}{12}=\frac{5}{12}

Comparando con las opciones, la respuesta correcta es la b).