¿Problemas estudiando matemáticas para la UNAM? Con este examen simulacro para carreras del área 2 podrás poner a prueba tus conocimientos con 24 ejercicios de todos los temas del examen de admisión.

Este examen simulacro es para quienes van a aplicar a las carreras del área 2 (Ciencias Biológicas, Químicas y de la Salud). Vamos a comenzar con los primeros 12 reactivos.
Recuerda que en la sección de materiales puedes encontrar la versión 1, así como más materiales para que sigas aprendiendo.
Es importante que estudies cada uno de los temas antes de pasar a resolver los ejercicios. Recuerda que en el curso de Unibetas puedes aprender todos los temas que vienen en el examen de admisión de la UNAM.
Estructura del examen
La prueba de ingreso a la UNAM tiene un total de 120 ejercicios. Para el área 2 veinticuatro pertenecen a matemáticas.
En la siguiente tabla te dejo la estructura del examen para el área 2, con las materias y el total de reactivos para cada una.
Estructura examen área 2.
| Temas | Área 2 |
|---|---|
| Español | 18 |
| Matemáticas | 24 |
| Física | 12 |
| Química | 13 |
| Biología | 13 |
| Historia universal | 10 |
| Historia de México | 10 |
| Literatura | 10 |
| Geografía | 10 |
| Filosofía | NA |
| Total | 120 |
De las 130 carreras ofertadas por la UNAM, 31 pertenecen al área 2. Además, 9 de esas 31 tienen modalidad de ingreso indirecto.
Temario matemáticas área 2
La siguiente lista contiene los temas de matemáticas para el área 2 de la UNAM.
- Operaciones con números reales, complejos y expresiones algebraicas
- Productos notables y factorización
- Ecuaciones
- Desigualdades
- Sistemas de ecuaciones
- Funciones algebraicas
- Trigonometría
- Funciones exponenciales y logarítmicas
- Recta
- Circunferencia
- Parábola
- Elipse
- Hipérbola
- Ecuación general de segundo grado
- Límites
- La derivada
- La integral
Simulador de matemáticas UNAM área 2
Procedemos con los reactivos del examen simulador versión 2 de matemáticas UNAM del área 2. Si alguno se te dificulta, salta al siguiente e inténtalo después.
Reactivo 1
Indica las coordenadas del centro de la circunferencia cuya ecuación general es {x}^{2}+{y}^{2}+4x-6y-3=0 .
- C\left(-1, 2\right)
- C\left(1, 2\right)
- C\left(4, 10\right)
- C\left(-2, 3\right)
Respuesta correcta: d).
Reactivo 2
Calcula el límite \underset{x\to 4}{\mathrm{lim}}\frac{\sqrt{x}-2}{x-4} .
- \frac{1}{4}
- -\frac{1}{2}
- \frac{1}{2}
- -\frac{1}{4}
Respuesta correcta: a).
Reactivo 3
¿Cuál es el coseno del ángulo A en el triángulo rectángulo siguiente?
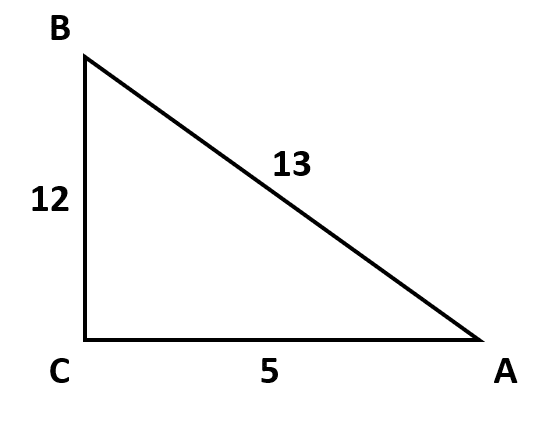
- \frac{5}{13}
- \frac{5}{12}
- \frac{12}{13}
- \frac{13}{12}
Respuesta correcta: a).
Reactivo 4
Factoriza la siguiente expresión.
10{n}^{4}-11{n}^{2}+3
- \left({n}^{2}-1\right)\left({n}^{2}+2\right)
- \left({n}^{2}-2\right)\left({n}^{2}+5\right)
- \left({n}^{2}-1\right)\left({n}^{2}-3\right)
- \left(2{n}^{2}-1\right)\left(5{n}^{2}-3\right)
Respuesta correcta: d).
Reactivo 5
Selecciona la expresión que corresponde a una inecuación:
- x>\frac{1}{2}
- 2x+1\le \frac{1}{2}x
- \frac{x+1}{2}=1
- {\mathrm{sec}}^{2}\left(x\right)-{\mathrm{tan}}^{2}\left(x\right)=1
Respuesta correcta: b).
Reactivo 6
Las soluciones de la ecuación 3{x}^{2}-5x-2=0 son:
- {x}_{1}=-2, {x}_{2}=\frac{1}{3}
- {x}_{1}=2, {x}_{2}=-\frac{1}{3}
- {x}_{1}=2, {x}_{2}=\frac{1}{3}
- {x}_{1}=7, {x}_{2}=2
Respuesta correcta: b).
Reactivo 7
Selecciona la desigualdad que tiene por solución al siguiente conjunto. \left[-\frac{4}{5},\infty \right)
- 3x-1\ge 0
- 4x-3\ge 8
- 4x-3\ge 2x-8
- 4x+4\le 9x+8
Respuesta correcta: d).
Reactivo 8
A partir del siguiente sistema de ecuaciones obtén el valor de x.
\begin{array}{c}x+y=-3\\ -3x+5y=-31\end{array}
- x=-3
- x=-1
- x=2
- x=1
Respuesta correcta: c).
Reactivo 9
Determina el rango de la función:
f\left(x\right)=1-3{\left(x+2\right)}^{2}
- y\in R, y\ge 1
- x\in R, y\in R
- x\in R, x\ge 2
- y\in R, y\le 1
Respuesta correcta: d).
Reactivo 10
Selecciona la función que tiene un desplazamiento de fase de \pi unidades a la derecha.
- f\left(x\right)=\mathrm{cos}\left(\pi x\right)
- f\left(x\right)=\mathrm{cos}\left(x+\pi \right)
- f\left(x\right)=\mathrm{cos}\left(x-\pi \right)
- f\left(x\right)=\pi \mathrm{cos}\left(x\right)
Respuesta correcta: c).
Reactivo 11
Se desea fabricar una caja sin tapa con una lámina de aluminio de 5 cm x 15 cm. ¿Cuánto se deberá cortar en cada esquina de la lámina para obtener el volumen máximo?
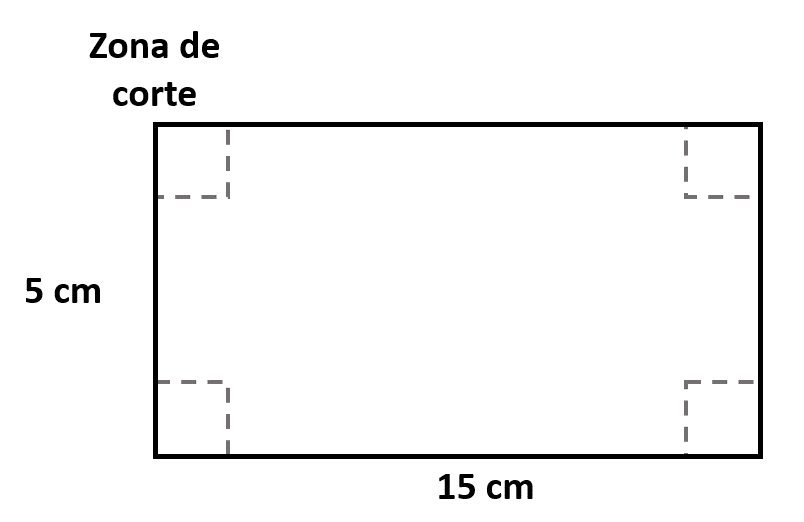
- \frac{45-\sqrt{21}}{6}
- \frac{45+\sqrt{21}}{6}
- \frac{20-5\sqrt{7}}{6}
- \frac{20+5\sqrt{7}}{6}
Respuesta correcta: c).
Reactivo 12
El punto medio del segmento que une a los puntos A\left(3m+1, m\right) y B\left(-m-1, m\right) es:
- \left(\frac{3}{2}, 2\right)
- \left(\frac{3m}{2}, 2m\right)
- \left(\frac{m}{3}, 2m\right)
- \left(m, m\right)
Respuesta correcta: d).

