¡Continuamos aspirante! Vamos la segunda y última parte del simulador de matemáticas UNAM por el área 2, vamos a conocer los reactivos del 13 al 24.

Date el tiempo de comprender cada tema de matemáticas, lo necesitarás al entrar a la carrera.
Simulador de matemáticas UNAM área 2
Damos paso a la segunda parte del simulador de matemáticas UNAM área 2 de las Ciencias Biológicas, Químicas y de la Salud.
Reactivo 13
La distancia del punto \left(-1, 2\right) a la recta dada por la ecuación 4x-3y+1=0 es:
- 0.2 unidades.
- 2 unidades.
- 1.25 unidades.
- 1.8 unidades.
Respuesta correcta: d).
Reactivo 14
Indica las coordenadas del centro de la circunferencia cuya ecuación general es {x}^{2}+{y}^{2}+2x-4y-20=0 .
- C\left(-1, 2\right)
- C\left(1, 2\right)
- C\left(4, 10\right)
- C\left(2, 5\right)
Respuesta correcta: a).
Reactivo 15
La ecuación de la parábola cuyo eje focal es x=0 , con el parámetro p=2 y vértice en el origen es:
- {x}^{2}+8y=0
- {y}^{2}-8x=0
- {y}^{2}+8x=0
- {x}^{2}-8y=0
Respuesta correcta: d).
Reactivo 16
Lugar geométrico en el plano en el que la distancia de cualquiera de los puntos a un punto fijo llamado centro es una cantidad constante.
- Elipse.
- Circunferencia.
- Hipérbola.
- Parábola.
Respuesta correcta: b).
Reactivo 17
La ecuación de la hipérbola centrada en el origen, con lado recto 24 y vértice V\left(0, -3\right) es:
- 9{y}^{2}-36{x}^{2}=324
- 36{y}^{2}-9{x}^{2}=324
- 9{y}^{2}-10{x}^{2}=90
- 10{y}^{2}-9{x}^{2}=90
Respuesta correcta: b).
Reactivo 18
Selecciona el criterio utilizado para definir que la ecuación de segundo grado A{x}^{2}+Bxy+C{y}^{2}+Dx+Ey+F=0 representa una hipérbola.
- {C}^{2}-4AB<0
- {B}^{2}-4AC>0
- {C}^{2}-4AB>0
- {B}^{2}-4AC<0
Respuesta correcta: b).
Reactivo 19
Calcula el límite \underset{x\to 0}{\mathrm{lim}}\frac{\sqrt{x+1}-1}{x} .
- \frac{\sqrt{2}}{2}
- -\frac{1}{\sqrt{2}}
- \frac{1}{\sqrt{2}}
- \frac{1}{2}
Respuesta correcta: d).
Reactivo 20
La derivada de la expresión y={x}^{\frac{1}{4}}-2{x}^{\frac{2}{3}} es:
- {y}^{\text{'}}=2{x}^{\frac{1}{2}}+6{x}^{\frac{1}{3}}
- {y}^{\text{'}}={x}^{\frac{1}{2}}+2{x}^{\frac{1}{3}}
- {y}^{\text{'}}=-\frac{1}{{x}^{\frac{1}{2}}}-\frac{2}{{x}^{\frac{2}{3}}}
- {y}^{\text{'}}=\frac{1}{4}{x}^{-\frac{3}{4}}-\frac{4}{3}{x}^{-\frac{1}{3}}
Respuesta correcta: d).
Reactivo 21
La derivada de f\left(x\right)=\sqrt{{x}^{2}+1} con respecto a x es:
- {f}^{\text{'}}\left(x\right)=\frac{x}{\sqrt{{x}^{2}+1}}
- {f}^{\text{'}}\left(x\right)=\frac{x}{\left({x}^{2}+1\right)}
- {f}^{\text{'}}\left(x\right)=\frac{x}{x\sqrt{{x}^{2}+1}}
- {f}^{\text{'}}\left(x\right)=\frac{x}{{x}^{2}+1}
Respuesta correcta: a).
Reactivo 22
Se desea fabricar una caja sin tapa con una lámina de aluminio de 20 cm x 25 cm. ¿Cuánto se deberá cortar en cada esquina de la lámina para obtener el volumen máximo?
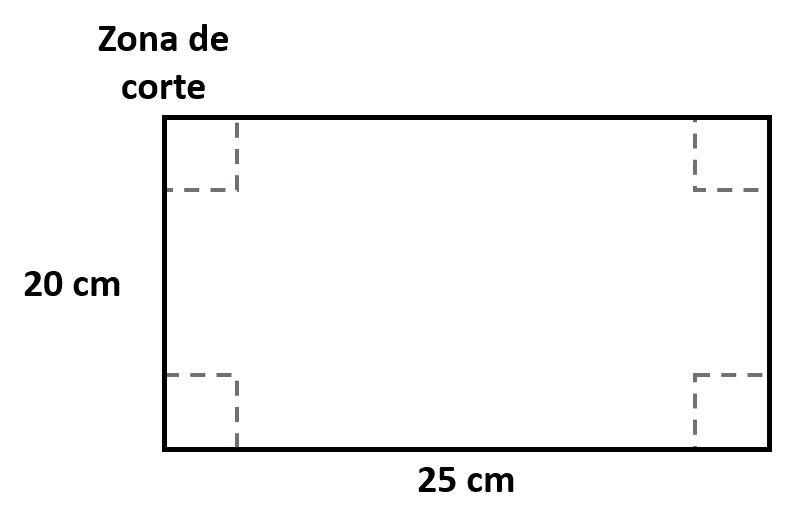
- \frac{45-\sqrt{21}}{6}
- \frac{45+\sqrt{21}}{6}
- \frac{45+5\sqrt{21}}{6}
- \frac{45-5\sqrt{21}}{6}
Respuesta correcta: d).
Reactivo 23
La \int {x}^{5/3}dx es igual a:
- \frac{1}{8}{x}^{\frac{8}{3}}+C
- \frac{3}{2}\sqrt{x}+C
- \frac{2}{3}\sqrt{x}+C
- \frac{3}{8}{x}^{\frac{8}{3}}+C
Respuesta correcta: d).
Reactivo 24
La \int {x}^{2}\left({x}^{3}+2x+1\right)dx es igual a:
- \frac{{x}^{6}}{6}+\frac{{x}^{4}}{2}+\frac{{x}^{3}}{3}+C
- \frac{{x}^{6}}{6}+\frac{{x}^{4}}{2}-\frac{{x}^{3}}{3}+C
- \frac{{x}^{6}}{6}-\frac{{x}^{4}}{2}-\frac{{x}^{3}}{3}+C
- {x}^{6}+{x}^{4}+{x}^{3}+C
Respuesta correcta: a).

