¡Hola aspirante! En este tutorial vamos a resolver paso a paso los primeros 10 reactivos de física, del 1 al 10, del Área 1 correspondiente a la guía de Ciencias Físico Matemáticas e Ingenierías de cara al examen de ingreso a la UNAM.

¿Cómo estudiar la guía? Te aconsejo desarrollarlos por tu cuenta antes de mirar la solución. Es importante que estudies y comprendas cada uno de los temas que van para el examen, tu calificación depende del esfuerzo que dediques durante tu preparación.
Este es un breve resumen sobre el examen de la Universidad Nacional Autónoma de México:
- Desarrollo: UNAM
- Área 1: Ciencias Físico Matemáticas e Ingenierías
- Materia: Física
- Reactivos: 120
- Tipo: Opción múltiple
- Duración: 3 horas
- Modalidades: Presencial
Estructura del examen
Recuerda que el examen de ingreso a la UNAM se compone de 120 reactivos, de los cuales 16 corresponden a la materia de física en el área 1 correspondiente a las carreras de Ciencias Físico-Matemáticas.
Además de física en el examen encontrarás otras 8 materias, la estructura del examen es la siguiente:
Estructura examen área 1
| Temas | Reactivos |
| Español | 18 |
| Matemáticas | 26 |
| Física | 16 |
| Química | 10 |
| Biología | 10 |
| Historia universal | 10 |
| Historia de México | 10 |
| Literatura | 10 |
| Geografía | 10 |
| Total | 120 |
Si tienes dudas sobre el proceso de ingreso a la UNAM, las carreras ofertadas o los aciertos necesarios, te recomiendo que ingreses a los siguientes tutoriales:
- Todo sobre la convocatoria de la UNAM
- Conoce los aciertos necesarios por carreras
- Lista completa de las carreras ofertadas por la universidad
- ¿Qué son las carreras de ingreso indirecto?
Temario física área 1
En física encontrarás 9 subtemas, de los cuales se desglosa un temario bastante extenso, por lo que es fundamental que organices tus tiempos de estudio.
- Cinemática
- Características de los fenómenos mecánicos
- Movimiento rectilíneo uniforme
- Movimiento uniformemente acelerado
- Fuerzas, leyes de Newton y Ley de la Gravitación Universal
- Factores que cambian la estructura o el estado de movimiento de objetos
- El concepto de fuerza
- El carácter vectorial de la fuerza
- Superposición de fuerzas
- Primera Ley de Newton
- Segunda Ley de Newton
- Concepto de peso
- Concepto de masa
- Tercera Ley de Newton
- Equilibrio rotacional y traslacional. Fuerza y torca
- Ley de la Fuerza en un resorte (Ley de Hooke)
- Ley de la Gravitación Universal. Movimiento de planetas
- Trabajo y leyes de la conservación
- Concepto de trabajo mecánico
- Concepto de potencia
- Energía cinética
- Energía potencial
- Conservación de la energía mecánica
- Conservación del ímpetu (momento)
- Colisiones entre partículas en una dimensión
- Procesos disipativos (fricción y rozamiento)
- Termodinámica
- Calor y temperatura
- Diferencia entre calor y temperatura
- Equilibrio térmico
- Escalas termométricas absolutas
- Conductividad calorífica y capacidad térmica específica
- Leyes de la Termodinámica
- Teoría Cinética de los Gases
- Estructura de la materia (enfoque clásico)
- Temperatura según la Teoría Cinética de los Gases
- Ecuación de estado de los gases ideales
- Calor y temperatura
- Ondas
- Caracterización de ondas mecánicas
- Reflexión y refracción de ondas
- Difracción e interferencia de ondas
- Energía de una onda incidente y de las ondas transmitida y reflejada
- Electromagnetismo
- Efectos cualitativos entre cuerpos cargados eléctricamente
- Ley de Coulomb. Campo eléctrico
- Ley de Ohm y potencia eléctrica
- Circuitos
- Circuitos de resistencias
- Circuitos de condensadores
- Campo magnético
- Inducción electromagnética
- Relación entre campo magnético y eléctrico
- Inducción de campos
- La luz como onda electromagnética
- Espectro electromagnético
- Leyes de Ampere-Maxwell
- Leyes de Faraday y Henry
- Fluidos
- Fluidos en reposo
- Presión atmosférica
- Principio de Pascal
- Principio de Arquímedes
- Presión hidrostática
- Tensión superficial y capilaridad
- Fluidos en movimiento
- Ecuación de continuidad
- Ecuación de Bernoulli
- Viscosidad
- Fluidos en reposo
- Óptica
- Reflexión y refracción de la luz
- Espejos planos y esféricos
- Lentes convergentes y divergentes
- Punto de vista contemporáneo (dualidad)
- Modelo corpuscular
- Modelo ondulatorio
- Física contemporánea
- Estructura atómica de la materia
- Modelos atómicos
- El experimento de Rutherford
- Espectroscopía y el modelo atómico de Bohr
- Física nuclear
- El descubrimiento de la radiactividad
- Decaimiento radiactivo
- Detectores de radiactividad
- Fisión y fusión nucleares
- Aplicaciones de la radiactividad y la energía nuclear
- Otras formas de energía
- Estructura atómica de la materia
Guía Física UNAM área 1 resuelta
Vamos con la solución paso a paso de los primeros 10 reactivos de física, para la guía de la Universidad Nacional Autónoma de México del área de Ciencias Físico Matemáticas y de las Ingenierías.
Reactivo 1
El desplazamiento de un ferrocarril se describe en la siguiente gráfica (posición x – tiempo t). A partir de los datos mostrados se puede deducir que el movimiento es rectilíneo con:
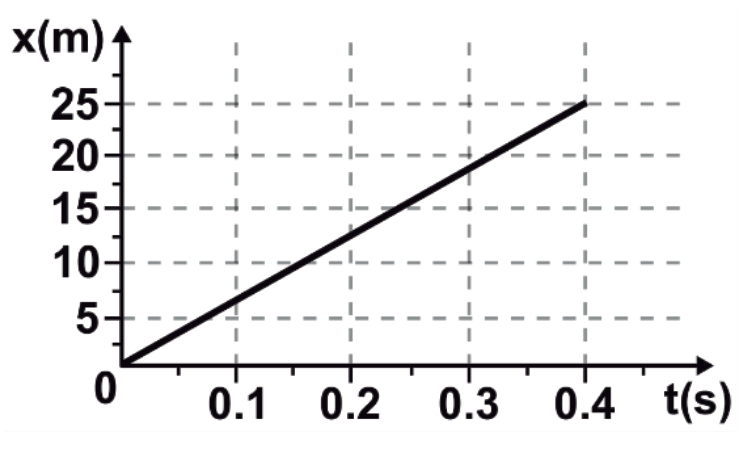
- Aceleración constante.
- Aceleración variable.
- Velocidad constante.
- Velocidad variable.
Solución:
Este problema se puede responder de dos formas: conociendo las gráficas del movimiento uniforme y acelerado o, utilizando las relaciones integro – diferenciales entre las variables cinemáticas. En este caso lo haremos con la gráfica y al final mostraremos el otro método.
Como sabemos, la velocidad mide la variación de la posición de un cuerpo respecto del tiempo. Desde el punto de vista matemático, esto se entiende como una razón o una pendiente. Como la gráfica de la posición es una línea recta, su pendiente es constante. La velocidad del ferrocarril es constante.
Teniendo en cuenta lo anterior, concluimos que la respuesta correcta es el inciso C. Si utilizamos la relación diferencial entre la posición y la velocidad:
v=\frac{ds}{dt}
Debido a que la posición es una línea recta, s\left(t\right)=mt+b , su derivada es constante.
v=\frac{d\left(mt+b\right)}{dt}=m
Reactivo 2
Un patinador describe un desplazamiento d con respecto del tiempo t como se muestra en la figura. ¿Cuál es la velocidad media del patinador en todo su recorrido?
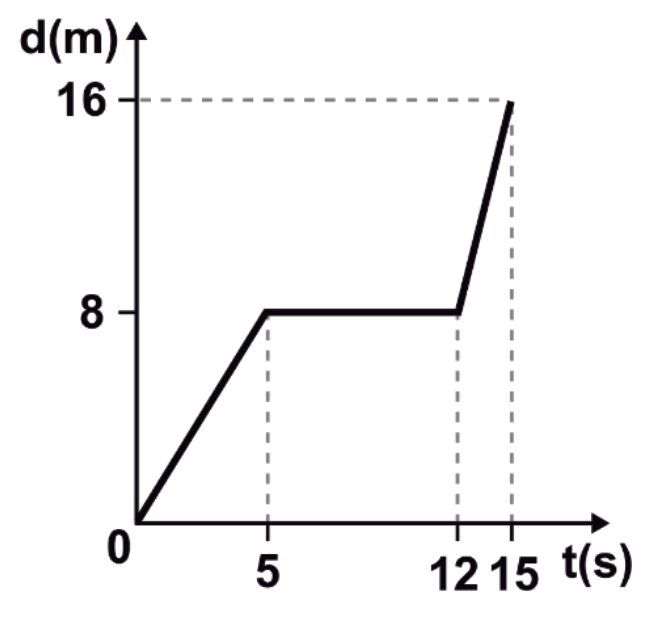
- 0.66\frac{\mathrm{m}}{\mathrm{s}}
- 1.06\frac{\mathrm{m}}{\mathrm{s}}
- 1.60\frac{\mathrm{m}}{\mathrm{s}}
- 2.80\frac{\mathrm{m}}{\mathrm{s}}
Solución:
La velocidad lineal media, es una magnitud escalar que mide el espacio recorrido en un intervalo de tiempo dado. Dicho cambio en el espacio recorrido se expresa en forma de distancia. Para efectos del ejercicio, el patinador recorre una distancia de 16 metros en 15 segundos.
La velocidad media sería:
{v}_{m}=\frac{16}{15}=1.06\frac{\mathrm{m}}{\mathrm{s}}
La respuesta correcta es el inciso B.
Reactivo 3
Sobre un cuerpo se aplicaron diferentes fuerzas en dirección horizontal y con el mismo sentido provocando que el objeto experimenta distintas aceleraciones. Basándote en la gráfica de los resultados obtenidos y despreciando la acción ejercida por la fricción entre el objeto y la superficie de contacto, ¿cuál es la masa del objeto?
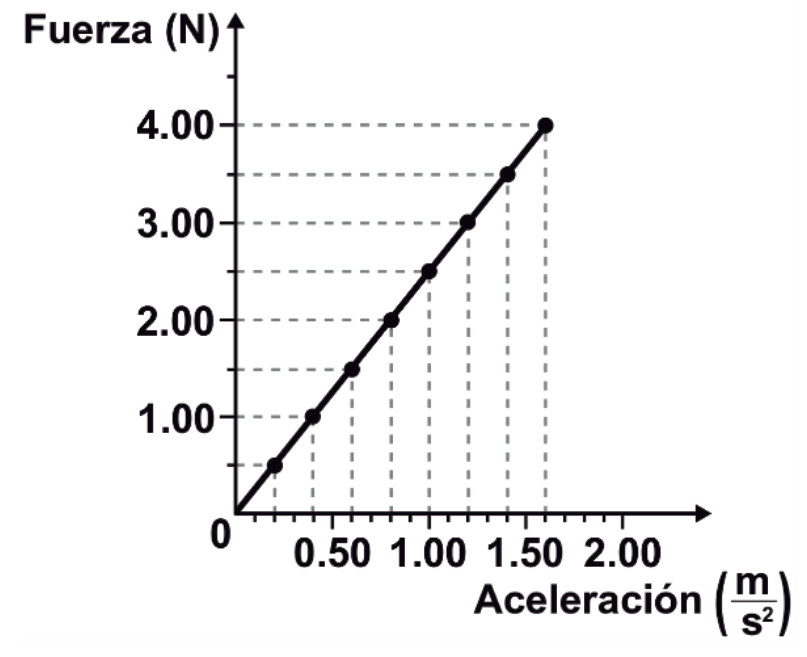
- 1.6 \mathrm{k}\mathrm{g}
- 2.5 \mathrm{k}\mathrm{g}
- 3.2 \mathrm{k}\mathrm{g}
- 4.0 \mathrm{k}\mathrm{g}
Solución:
La segunda ley de Newton nos dice que la fuerza neta aplicada sobre un cuerpo, es igual al producto de la masa por su aceleración.
\overrightarrow{F}=m\overrightarrow{a}
Debido a que el movimiento es lineal, podemos prescindir de los vectores.
F=ma
Ya que el enunciado establece que no existe fuerza de rozamiento entre el cuerpo y la superficie, la fuerza neta es la aplicada en cada caso.
Comparando la ecuación F=ma con la gráfica, vemos que F es la variable y , mientras que la aceleración es la variable x en la ecuación de la recta. La masa corresponde a la pendiente. De esta forma, podemos calcular la masa al sustituir cualquier punto \left(a, F\right) extraído de la gráfica.
Seleccionamos \left(a, F\right)=\left(1, 2.5\right) :
m=\frac{F}{a}=\frac{2.5}{1}=2.5 \mathrm{k}\mathrm{g}
La respuesta correcta es el inciso B.
Reactivo 4
Sobre un objeto de 100 kg se aplican dos fuerzas (una de 20 N y otra de 30 N) con la misma dirección, pero de sentido contrario, ¿cuál es la magnitud de la aceleración del objeto?
- 0.1\frac{\mathrm{m}}{{\mathrm{s}}^{2}}
- 0.2\frac{\mathrm{m}}{{\mathrm{s}}^{2}}
- 0.3\frac{\mathrm{m}}{{\mathrm{s}}^{2}}
- 0.5\frac{\mathrm{m}}{{\mathrm{s}}^{2}}
Solución:
Hagamos una sencilla representación gráfica de la situación planteada en el enunciado. Asumiremos que la fuerza de 20 N se aplica hacia la derecha y que la de 30 N se aplica hacia la izquierda.
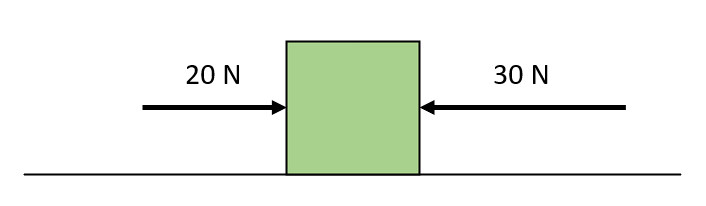
La fuerza neta sobre el bloque, aplicando la segunda ley de Newton es:
\overrightarrow{F}=20\widehat{i}-30\widehat{i}=m\overrightarrow{a}
Simplificando:
\overrightarrow{a}=-\frac{10\widehat{i} \mathrm{N}}{100 \mathrm{k}\mathrm{g}}=-0.1\widehat{i}\frac{\mathrm{m}}{{\mathrm{s}}^{2}}
El módulo de la aceleración es:
\left|\overrightarrow{a}\right|=0.1\frac{\mathrm{m}}{{\mathrm{s}}^{2}}
Seleccionamos como respuesta correcta el inciso A.
Reactivo 5
La Ley de Hooke sobre la relación entre desplazamiento x del resorte y la fuerza F, como se muestra en la figura, establece que x es
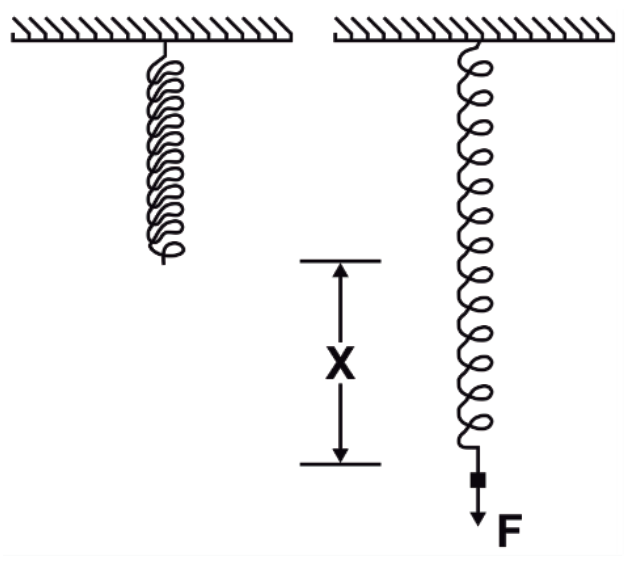
- directamente proporcional a F.
- inversamente proporcional a F.
- directamente proporcional al cuadrado de F.
- inversamente proporcional al cuadrado de F.
Solución:
La ley de Hooke establece que la fuerza de compresión o estiramiento aplicada sobre éste, es directamente proporcional al estiramiento o compresión ejercido sobre el resorte, pero en sentido contrario. La constante de proporcionalidad entre la fuerza y el desplazamiento se denomina constante elástica k .
F=-k\mathrm{\Delta }x
Con esta información y examinado a los incisos, concluimos que la respuesta correcta es A.
Reactivo 6
Un niño está parado sobre un carrito, ambos en reposo, el primero pesa 30 kg y cuando salta hacia adelante a 2 m/s, el carrito es lanzado hacia atrás a 12 m/s. Si se desprecia la fricción, ¿cuál es la masa del carrito?
- 6 kg
- 5 kg
- 5 kg
- 8 kg
Solución:
Para resolver este problema, empleamos el principio de conservación del momento lineal para sistemas cerrados. En nuestro caso, el sistema es el conjunto niño – carrito. Existen dos instantes de interés en el problema: el momento antes del salto 1 y el momento después del salto 2 .
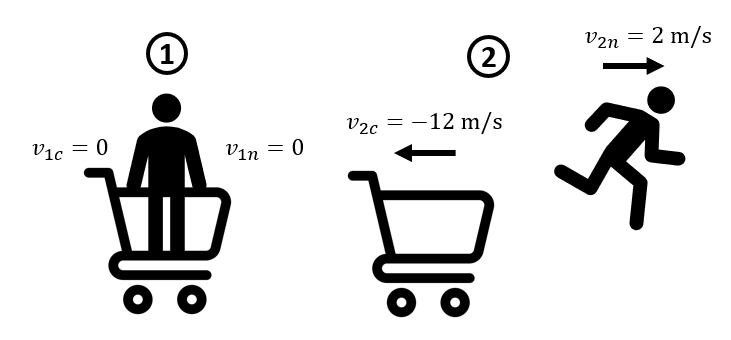
La conservación del momento lineal nos dice que:
\overrightarrow{{p}_{1}}=\overrightarrow{{p}_{2}}
En el instante 1, el sistema niño – carrito se encuentra en reposo, el momento lineal acá es cero.
\overrightarrow{{p}_{1}}=\overrightarrow{{v}_{1}}\left({m}_{c}+{m}_{n}\right)=\left(0\right)\left({m}_{c}+{m}_{n}\right)=0
Por lo tanto:
\overrightarrow{{p}_{2}}={m}_{n}{v}_{n2}+{m}_{c}{v}_{c2}=0
En el instante 2, tenemos al niño de masa {m}_{n} y velocidad \overrightarrow{{v}_{n2}}=2\widehat{i} \mathrm{m}/\mathrm{s} y el carrito con masa {m}_{c} y velocidad \overrightarrow{{v}_{c2}}=-12\widehat{i} \mathrm{m}/\mathrm{s} . Despejamos la masa del carrito.
{m}_{n}{v}_{n2}+{m}_{c}{v}_{c2}=0\to {m}_{c}=-\frac{{m}_{n}{v}_{n2}}{{v}_{c2}}
Sustituimos.
{m}_{c}=-\frac{\left(30\right)\left(2\right)}{-12}=5 \mathrm{k}\mathrm{g}
La masa del carrito es igual a 5 kilogramos.
Seleccionamos como respuesta correcta al inciso B.
Reactivo 7
Un balín X de masa igual a 200 g rueda con velocidad V, con fricción despreciable y en posición horizontal sobre un riel recto. Otro balín Y de masa igual a 400 g rueda con velocidad −V sobre el mismo riel, pero en sentido contrario (ver figura). ¿Cuál será la velocidad del balín X después del choque totalmente elástico, si Y queda inmóvil?
Considera:
Hay conservación de energía e ímpetu. Los balines se comportan como partículas.
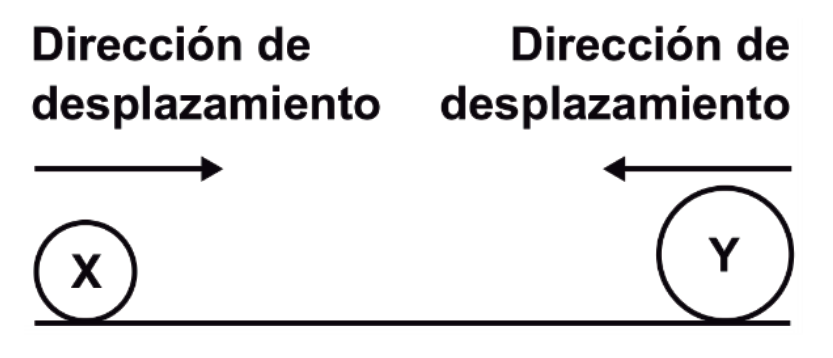
- {v}_{x}=0
- {v}_{x}=-0.5V
- {v}_{x}=-V
- {v}_{x}=-0.25V
Solución:
En un choque perfectamente elástico no ocurre pérdida de energía y, por ende, se cumple el principio de conservación del momento lineal. Este problema se puede resolver aplicando un balance de energía o mediante la conservación de p .
Emplearemos el método de conservación del momento lineal.
\overrightarrow{{p}_{1}}=\overrightarrow{{p}_{2}}
Debido a que el choque es unidimensional, podemos prescindir de la notación vectorial siempre que respetemos el signo de las cantidades. Ahora, debemos definir el signo de las velocidades para el instante previo y posterior al choque.
Antes del choque.

{p}_{1}={m}_{x}V-{m}_{y}V
Luego del choque.

{p}_{2}={m}_{x}{v}_{x2}
Igualamos las ecuaciones:
{m}_{x}V-{m}_{y}V={m}_{x}{v}_{x2}
Despejamos la velocidad de la bola X .
{v}_{x2}=\frac{V\left({m}_{x}-{m}_{y}\right)}{{m}_{x}}
Evaluamos. Las masas se deben sustituir en kilogramos.
{v}_{x2}=\frac{V\left(0.2-0.4\right)}{0.2}=-V\frac{0.2}{0.2}=-V
La velocidad del balín X luego del choque es igual a -V .
Indicamos como respuesta correcta al inciso C.
Reactivo 8
Un termómetro de gas a volumen constante es usado para medir la temperatura de un objeto. Cuando el termómetro está en contacto con el punto triple del agua (273.17 K), la presión en el termómetro es \mathrm{8,500}\times {10}^{4} Pa. Cuando éste entra en contacto con otro objeto la presión es de \mathrm{9,650}\times {10}^{4} Pa. ¿Cuál es la temperatura del objeto?
Considera:
El gas del termómetro se comporta como un gas ideal.
- 683 K
- 310 K
- 410 K
- 241 K
Solución:
Para resolver este problema, debemos utilizar la ley de Gay-Lussac para gases ideales en procesos a volumen constante:
\frac{{P}_{1}}{{T}_{1}}=\frac{{P}_{2}}{{T}_{2}}
La presión y temperatura 1 corresponden a los valores del punto triple del agua. Despejamos la temperatura 2 de la ecuación:
{T}_{2}={T}_{1}\frac{{P}_{2}}{{P}_{1}}
Sustituimos.
{T}_{2}=\left(273.17\right)\frac{9.650\times {10}^{4}}{8.500\times {10}^{4}}=310.13 \mathrm{K}
Cuando la presión del gas es de 9.650\times {10}^{4} \mathrm{P}\mathrm{a} , la temperatura es igual a 310.13 \mathrm{K} .
Concluimos indicando como respuesta correcta al inciso B.
Reactivo 9
Para convertir un valor de temperatura Celsius {T}_{C} a su valor equivalente en la escala Kelvin {T}_{K} de temperaturas, se emplea la expresión:
- {T}_{K}=\frac{\left({T}_{C}-32\right)}{1.8}
- {T}_{K}={T}_{C}+273
- {T}_{K}={T}_{C}-273
- {T}_{K}=1.8\left({T}_{C}+273\right)
Solución:
Para responder este problema, es necesario que conozcas de antemano la fórmula para convertir una lectura en grados Celsius a grados Kelvin. Dicha ecuación es:
{T}_{K}=273+{T}_{C}
La respuesta correcta es el inciso B.
Reactivo 10
Una onda formada en una cuerda tiene una longitud de onda de 10 cm y un periodo de 2 s, ¿con qué velocidad se propaga?
- 20.00\frac{\mathrm{c}\mathrm{m}}{\mathrm{s}}
- 0.25\frac{\mathrm{c}\mathrm{m}}{\mathrm{s}}
- 5.00\frac{\mathrm{c}\mathrm{m}}{\mathrm{s}}
- 2.00\frac{\mathrm{c}\mathrm{m}}{\mathrm{s}}
Solución:
Para calcular la velocidad de propagación de cualquier onda, empleamos la siguiente ecuación:
v=\frac{\lambda }{\tau }
Sustituimos la longitud de onda y periodo.
v=\frac{10 \mathrm{c}\mathrm{m}}{2 \mathrm{s}}=5.00\frac{\mathrm{c}\mathrm{m}}{\mathrm{s}}
La velocidad de propagación de la onda es igual a 5 centímetros por segundo.
La respuesta correcta es el inciso C.


