¡Llegamos a la última parte aspirante! Vamos con la solución de la segunda parte de los reactivos de física del área 1, en este caso del 11 al 16, en la guía de Ciencias Físico Matemáticas y de las Ingenierías como preparación al examen de ingreso a la UNAM.

Este es un breve resumen sobre el examen de la UNAM:
- Desarrollo: UNAM
- Área 1: Ciencias Físico Matemáticas y de las Ingenierías
- Materia: Física
- Reactivos: 120
- Tipo: Opción múltiple
- Duración: 3 horas
- Modalidades: Presencial
Física es una asignatura con una gran extensión teórica y es muy difícil aprobarla sin comprender los fundamentos. Te recomiendo estudiar los fundamentos teóricos antes de entrar por completo a los reactivos.
Ejercicios resueltos de Física UNAM
Vamos con los últimos 6 ejercicios de física de la guía Ciencias Físico Matemáticas e Ingenierías UNAM. Recuerda tomar descansos, esto es importante para afianzar los conocimientos adquiridos.
No olvides que tienes un tiempo límite para responder el examen.
Te invito a continuar aprendiendo con el resto de guías resueltas de la UNAM, maratones de reactivos y clases.
Reactivo 11
La interferencia de dos ondas mecánicas puede generar franjas claras y obscuras. Lo anterior se debe a la conservación de la
- Polarización
- Difracción
- Energía
- Longitud de onda
Solución:
Las ondas mecánicas que se propagan a través de un medio material considerado ideal no pierden energía, esto es debido a que el medio no presenta disipación en forma de calor debido a la propagación de la onda.
Como consecuencia de esto, cuando dos o más ondas mecánicas se encuentran en un punto del medio en el que se propagan, estas se interfieren mutuamente de forma local para luego continuar cada una propagándose en su dirección correspondiente.
Si no se conserva la energía, en el momento en el que las ondas se interfieren, ambas pierden energía en forma de calor a través del medio y el resultado será una onda extinta o de menor amplitud.
Teniendo en cuenta lo anterior, concluimos que la respuesta correcta es el inciso C. Otra forma de resolver el problema, consiste en aplicar la lógica. De los cuatro incisos, solo la energía se conserva.
Reactivo 12
Por un cable que tiene una resistencia eléctrica de 10\mathrm{\Omega } , circula una corriente eléctrica de 10 A. ¿Cuál es el voltaje en el cable?
- 100 V
- 20 V
- 10 V
- 1 V
Solución:
Para calcular la diferencia de potencial que cae en una resistencia eléctrica cuando circula una corriente por ella, empleamos la ley de Ohm.
R=\frac{V}{I}
Despejamos el voltaje y sustituimos.
V=IR
V=\left(10\right)\left(10\right)=100 \mathrm{V}
La caída de tensión en el cable es de 100 Voltios cuando por él circula una corriente de 10 Amperios. La respuesta correcta es el inciso A.
Reactivo 13
Determina la resistencia total del circuito que se representa en la imagen.
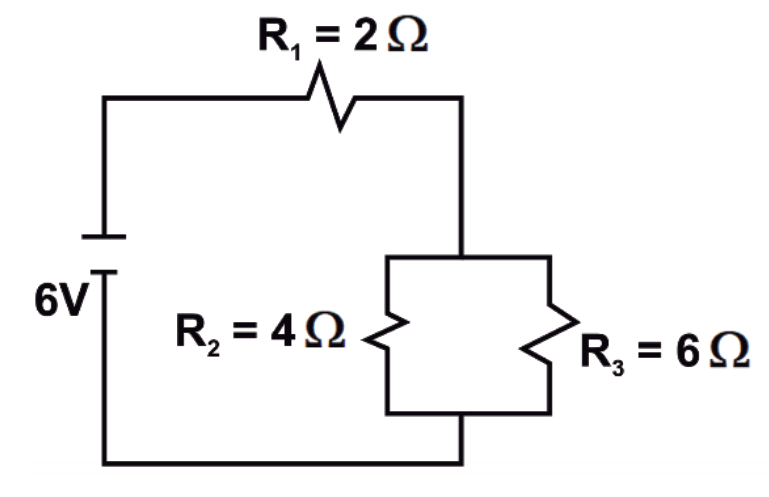
- 2.41 \mathrm{\Omega }
- 4.4 \mathrm{\Omega }
- 12 \mathrm{\Omega }
- 1.90 \mathrm{\Omega }
Solución:
Cuando un ejercicio solicita calcular la resistencia equivalente, se debe indicar respecto a cual punto del circuito se debe hacer. En este caso, se entiende que debemos calcular la resistencia total vista por la fuente 6 voltios.
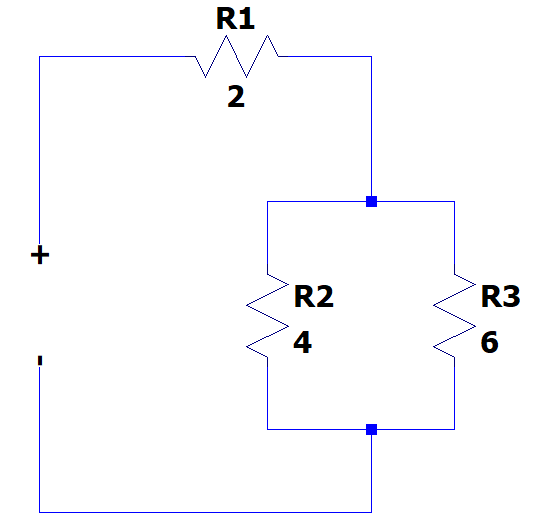
Iniciamos resolviendo el paralelo entre {R}_{2} y {R}_{3} .
{R}_{\mathrm{2,3}}=\frac{\left(4\right)\left(6\right)}{4+6}=\frac{24}{10}=2.4 \mathrm{\Omega }
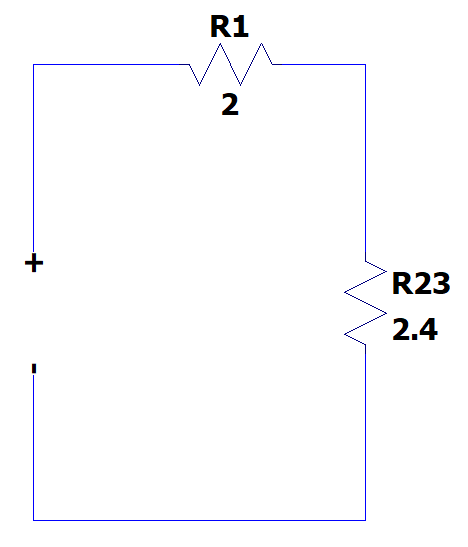
La resistencia vista por la fuente es igual a resolver la serie entre {R}_{1} y {R}_{\mathrm{2,3}} .
{R}_{e}={R}_{1}+{R}_{\mathrm{2,3}}=2+2.4=4.4 \mathrm{\Omega }
Comparando con los incisos, la respuesta correcta es B.
Reactivo 14
¿En cuánto tiempo se llenará una alberca olímpica de 50 m x 25 m x 3 m, si se usa un tubo de 40 cm de diámetro por el que fluye agua a una velocidad de 4 m/s ?
- 0.0052 \mathrm{h}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{s}
- 0.020 \mathrm{h}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{s}
- 1.63 \mathrm{h}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{s}
- 2.07 \mathrm{h}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{s}
Solución:
Para resolver este problema, debemos utilizar la ecuación de flujo volumétrico.
Q=A\cdot v
Donde A es la sección transversal del tubo por el que fluye la sustancia y v , es la velocidad con la que fluye. A su vez, el flujo volumétrico es igual al volumen total extraído por el tiempo que tardó en vaciarse el tanque.
Q=\frac{V}{t}
La velocidad es un dato directo del enunciado, nos queda calcular el área de sección transversal del tubo.
Área del tubo circular.
A=\frac{\pi {D}^{2}}{4}
Sustituimos el diámetro en metros.
A=\frac{\pi {\left(0.4\right)}^{2}}{4}=0.1256 {\mathrm{m}}^{2}
Calculamos el volumen total del tanque.
V=\left(50\right)\left(25\right)\left(3\right)=3750 {\mathrm{m}}^{3}
Ahora, despejamos el tiempo de vaciado.
Av=\frac{V}{t}\to t=\frac{V}{Av}
Sustituimos los valores.
t=\frac{3750}{\left(0.1256\right)\left(4\right)}=7464.2 \mathrm{s}\mathrm{e}\mathrm{g}
Convertimos este tiempo en horas.
t=7464.2 \mathrm{s}\mathrm{e}\mathrm{g}\cdot \frac{1 \mathrm{h}}{3600 \mathrm{s}\mathrm{e}\mathrm{g}}=2.07 \mathrm{h}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{s}
El tanque tardará 2.07 horas en vaciarse a través de la tubería de 40 cm de diámetro.
La respuesta correcta es el inciso D.
Reactivo 15
A través de una lente convergente de 30 cm de radio pasan rayos que forman una imagen a 20 cm de distancia de la lente. ¿A qué distancia se encuentra el objeto real del lente?
- 30 cm
- 16 cm
- 8 cm
- 60 cm
Solución:
Para calcular la distancia a la que se encuentra el objeto real, empleamos la ecuación de la lentes delgadas:
\frac{1}{f}=\frac{1}{o}+\frac{1}{i}
Donde f es la distancia focal, o es la distancia del objeto e i es la distancia de la imagen. En este caso no tenemos la distancia focal, pero la podemos calcular con la siguiente ecuación:
f=\frac{R}{2}
Sustituimos el radio de la lente convergente.
f=\frac{30}{2}=15 \mathrm{c}\mathrm{m}
Ahora, calculamos la distancia del objeto.
\frac{1}{f}=\frac{1}{o}+\frac{1}{i}\to o=\frac{fi}{i-f}
Evaluamos.
o=\frac{\left(20\right)\left(15\right)}{20-15}=60 \mathrm{c}\mathrm{m}
El objeto se encuentra a 60 centímetros de la lente.
Concluimos indicando como respuesta correcta al inciso D.
Reactivo 16
¿En qué áreas recibió Madame Curie el premio Nobel?
- Física y Biología
- Medicina y Química
- Química y Biología
- Física y Química
Solución:
Marie Curie fue una físico, matemática y química de origen polaco, cuyo principal reconocimiento se debe a sus investigaciones acerca de la radioactividad de los materiales.
En 1903 recibió el premio Nobel de Física gracias al descubrimiento de la radioactividad y de nuevo en 1914, ahora en química, por sus estudios acerca del radio. Fue la primera persona en toda la historia de los premios Nobel en obtener 2 distinciones.
Con este breve recuento de los galardones recibidos por Marie Curie, concluimos que la respuesta correcta es el inciso D.

