Continúa la solución de la segunda parte del examen simulador de matemáticas del nuevo ExIES, desde el reactivo 11 hasta el 20, como preparación al examen de ingreso de la UABC.

Resuélvelos por tu cuenta antes de revisar la solución y no olvides tomar el tiempo. Además de dominar los remas, debes acortar el tiempo que tardas en resolver los problemas.
Reactivo 11
En el siguiente sistema de ecuaciones, calcular el valor de x:
\begin{array}{c}x+y+z=22\\ 4y+5z=44\\ z=4\end{array}
- 24
- 6
- 10
- 12
Solución:
A partir del valor de z y de la segunda ecuación, podemos calcular a y .
4y+5z=44\to 4y=44-5z
4y=44-5\left(4\right)=24
\therefore y=6
Finalmente, sustituimos el valor de z y y en la expresión para calcular a x .
x=22-y-z
\therefore x=22-6-4=12
El valor de x que satisface al sistema de ecuaciones es 12.
La respuesta correcta es el inciso d).
Reactivo 12
Encuentra las raíces de la siguiente ecuación: 12{x}^{2}-x-6=0 .
- -2/3, -3/4
- -2/3, 3/4
- 2/3, -3/4
- 2/3, 3/4
Solución:
Tenemos dos opciones para resolver este problema:
- Aplicamos la ecuación de segundo grado
- Probamos los valores de los incisos hasta encontrar la respuesta correcta
En este caso, vamos a aplicar la ecuación de segundo grado.
{x}_{\mathrm{1,2}}=\frac{-b\pm \sqrt{{b}^{2}-4ac}}{2a}
Sustituimos a=12, b=-1, c=-6 .
{x}_{\mathrm{1,2}}=\frac{-\left(-1\right)\pm \sqrt{{\left(-1\right)}^{2}-4\left(12\right)\left(-6\right)}}{2\left(12\right)}=\frac{1\pm \sqrt{1+288}}{24}=\frac{1\pm \sqrt{289}}{24}
La raíz cuadrada de 289 es 17.
{x}_{\mathrm{1,2}}=\frac{1\pm 17}{24}
{x}_{1}=\frac{18}{24}=\frac{3}{4}
{x}_{2}=\frac{16}{24}=\frac{2}{3}
Las raíces del trinomio son: 2/3, 3/4.
La respuesta correcta es el inciso d).
Reactivo 13
Una función base cuadrática tiene su forma algebraica: y = {x}^{2} .
La cual realizará dos desplazamientos: 5 unidades hacia la derecha y 2 unidades hacia arriba. ¿Cuál de las siguientes opciones, representa dichos desplazamientos?
- y={\left(x+5\right)}^{2}+2
- y={\left(x+5\right)}^{2}-2
- y={\left(x-5\right)}^{2}+2
- y={\left(x-5\right)}^{2}-2
Solución:
Para desplazar una función en el plano cartesiano, debemos recordar que signo debe tener el desplazamiento horizontal h y el vertical k . Teniendo en cuenta que:
Horizontal: x\pm h
Vertical: y\pm k
Desplazamiento horizontal. El movimiento es hacia la izquierda cuando h es positivo y hacia la derecha cuando h es negativo.
Desplazamiento vertical. El movimiento es hacia abajo cuando k es positivo y hacia arriba cuando k es negativo.
Examinando el enunciado, h=-5 porque es hacia la derecha y k=-2 porque es hacia arriba. Sustituyendo en la expresión nos queda:
y-2={\left(x-5\right)}^{2}
Despejando a y :
y={\left(x-5\right)}^{2}+2
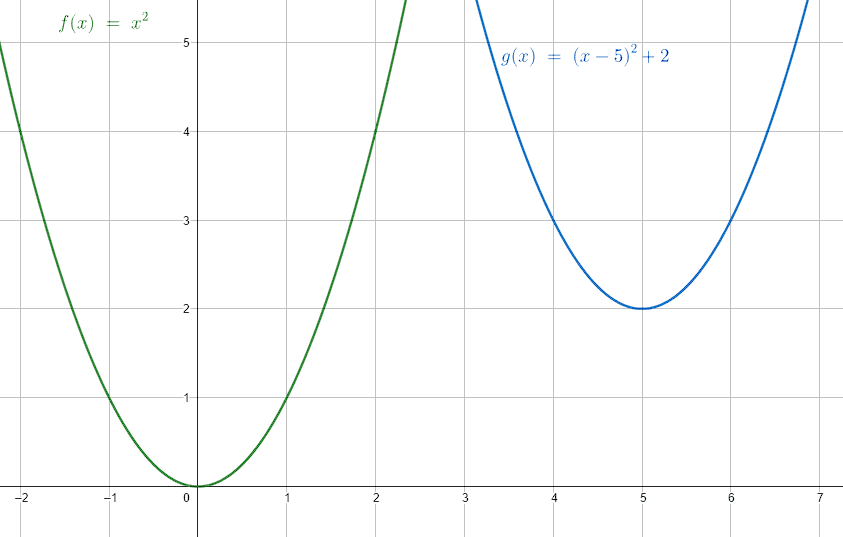
La respuesta correcta al problema se encuentra en el inciso c).
Reactivo 14
Se aplicó un examen de admisión dentro de una universidad, en Baja California. De los 240 aspirantes que aplicaron, quedaron seleccionados 100 de Mexicali, 50 de Tijuana y 30 de Ensenada. ¿Qué porcentaje de aspirantes no quedaron seleccionados?
- 25%
- 35%
- 50%
- 75%
Solución:
El porcentaje de estudiantes rechazados se calcula como el cociente de los rechazados sobre el total de aspirantes por 100.
P{R}_{\%}=\frac{ER}{\mathrm{T}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}\cdot 100\%
El número de estudiantes rechazados se obtiene restándole al total, la cantidad de aspirantes seleccionados.
ER=240-100-50-30=60
Sustituimos en la expresión del porcentaje y resolvemos.
P{R}_{\%}=\frac{60}{240}\cdot 100\%=25\%
El 25% de los aspirantes no fueron seleccionados.
Concluimos indicando como respuesta correcta la opción a).
Reactivo 15
Una población de bacterias (P), se duplica cada hora (t), mediante la función: P={P}_{o}\cdot {2}^{t} .
Donde Po es la cantidad inicial de bacterias presentes. ¿Cuánta población de bacterias existe, si se tiene una población inicial de 100 bacterias y han transcurrido 3 horas?
- 200 bacterias
- 300 bacterias
- 600 bacterias
- 800 bacterias
Solución:
El modelo matemático para la evolución de las bacterias es la función exponencial que indica el enunciado. Para obtener el total de bacterias transcurridas las 3 horas, sustituimos t=3 y {P}_{o}=100 .
P=\left(100\right)\cdot {2}^{3}=800 \mathrm{b}\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{a}\mathrm{s}
La respuesta correcta es el inciso d).
Reactivo 16
¿Cuál es la solución del siguiente sistema de ecuaciones?
\begin{array}{c}y=3x+2\\ y={x}^{2}+2x-4\end{array}
- \left(-11, 3\right),\left(-4, -2\right)
- \left(-3, 11\right),\left(2, 4\right)
- \left(3, 11\right),\left(-2, -4\right)
- \left(11, 3\right),\left(4, 2\right)
Solución:
Iniciamos igualando las ecuaciones a través de la variable y .
3x+2={x}^{2}+2x-4
Simplificamos e igualamos a cero.
{x}^{2}-x-6=0
Buscamos dos números que sumados sean -1 y multiplicados -6. Estas cantidades son -3 y 2.
{x}^{2}-x-6=\left(x-3\right)\left(x+2\right)=0
La igualdad se cumple cuando:
x=3, x=-2
Con estos valores de x , podemos ir a los incisos para descartar opciones o seleccionar la respuesta correcta. La única opción cuyos puntos tienen como abscisas 3 y -2 es el c). Por lo tanto, la respuesta correcta del problema es el inciso c).
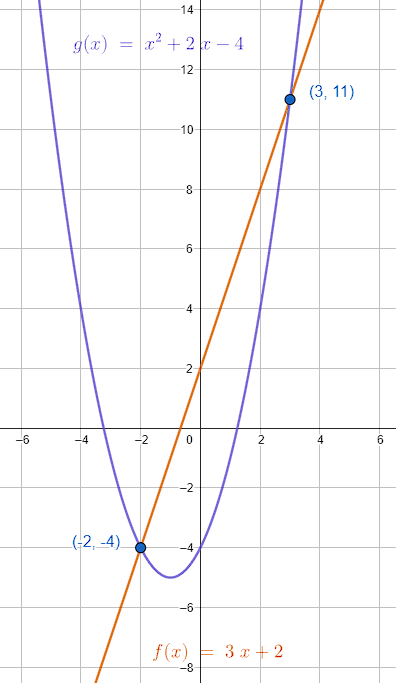
Reactivo 17
El comportamiento de una función polinomial, se muestra a continuación:
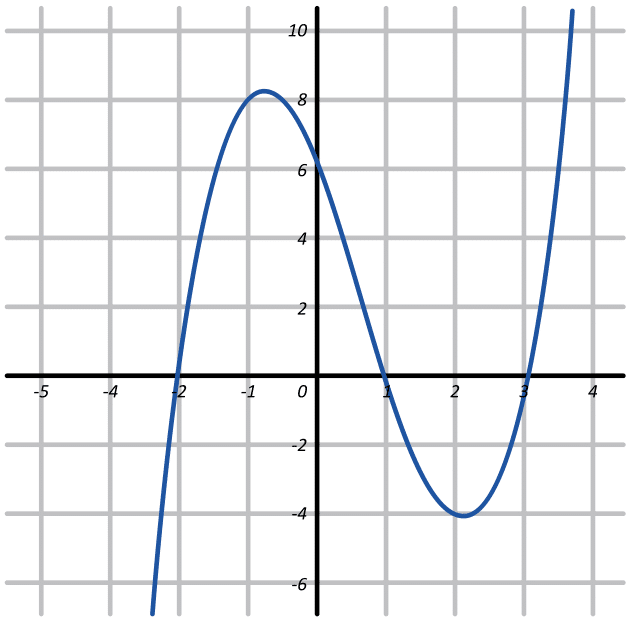
- -2, -1, 3
- -2, 1, 3
- -2, 0, 3
- 1, 2, 3
Solución:
Las raíces o ceros de un polinomio P\left(x\right) , son aquellos valores de x que anulan la función polinómica. Desde el punto de vista gráfico, las raíces son los cortes con el eje x que presenta la función polinómica.
Teniendo en cuenta lo anterior y examinando la gráfica del enunciado, las raíces del polinomio son: -2, 1 y 3. Concluimos que la respuesta correcta es el inciso b).
Reactivo 18
Una persona que mide 1.5 m de altura, forma una sombra de 2 m sobre el suelo, mientras que un poste de altura x, forma una sombra de 6 m sobre el suelo. ¿Cuál es el modelo matemático, que permite calcular la altura del poste?
- \frac{1.5}{x}=\frac{6}{2}
- \frac{1.5}{6}=\frac{2}{x}
- \frac{2}{1.5}=\frac{x}{6}
- \frac{1.5}{2}=\frac{x}{6}
Solución:
Iniciemos representado mediante un dibujo la situación planteada por el enunciado.
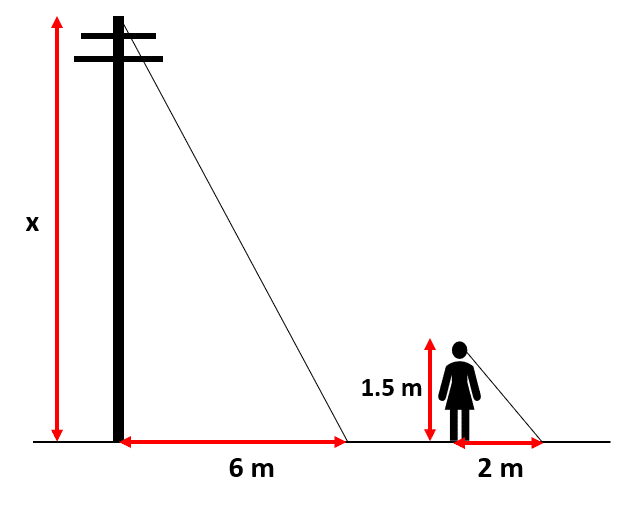
A partir de la imagen, vemos que los triángulos que se forman son semejantes. Aplicando la fórmula de semejanza de triángulos sobre los catetos nos queda:
\frac{x}{6}=\frac{1.5}{2}
Este modelo matemático permite calcular la altura del poste.
Indicamos como respuesta correcta al inciso d).
Reactivo 19
Un establo en forma triangular necesita una cerca que cubra alrededor del área para que el ganado se mantenga protegido en todo momento del día. La medida de los catetos que conforman dicho establo son 30 m y 40 m, respectivamente. ¿Cuántos metros de cerca se necesitan para cubrir todo el perímetro del establo?
- 50 m
- 70 m
- 120 m
- 170 m
Solución:
Aunque el enunciado no lo dice de forma explícita, el estable tiene forma de triángulo rectángulo, esto también se puede deducir porque nos hablan de catetos y no de lados o aristas. El perímetro del triángulo es igual a la suma de los dos catetos y la hipotenusa.
P=H+{C}_{1}+{C}_{2}
La longitud de la hipotenusa se calcula aplicando el teorema de Pitágoras.
H=\sqrt{{30}^{2}+{40}^{2}}=\sqrt{250}=50 \mathrm{m}
Sustituimos.
P=50+30+40=120 \mathrm{m}
Se necesitan al menos 120 metros de cerca.
La respuesta correcta es el inciso c). Los números 50, 40 y 30 forman una terna pitagórica, por eso se puede calcular la hipotenusa sin el uso de calculadora.
Reactivo 20
Una bailarina de ballet posa para una fotografía, justo como se muestra en la figura:
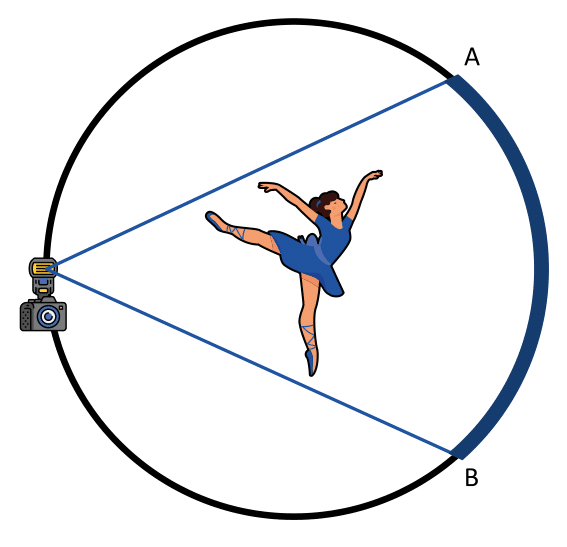
Si el ángulo que forma la luz de la cámara es de 50°, determina el valor del arco \widehat{AB} .
- 50°
- 75°
- 100°
- 125°
Solución:
Para calcular la apertura del arco AB , empleamos la fórmula del ángulo inscrito en la circunferencia.
\angle \mathrm{c}\mathrm{á}\mathrm{m}\mathrm{a}\mathrm{r}\mathrm{a}=\frac{\widehat{AB}}{2}
Despejamos al arco y calculamos.
\widehat{AB}=2\angle \mathrm{c}\mathrm{á}\mathrm{m}\mathrm{a}\mathrm{r}\mathrm{a}=2\left(50°\right)=100°
El arco tiene una apertura de 100°.
La respuesta correcta es el inciso c).


