Simulador UABC Matemáticas | 30 ejercicios resueltos

En este simulacro de examen vamos a resolver 30 ejercicios de matemáticas basados en los temas de la nueva guía de estudios de la UABC.

¿Nueva? Sí, acaban de cambiar el examen y el examen que vas a aplicar se llama ExIES, si quieres conocerlo al post de la guía UABC 2023 para conocer el temario completo del examen.

Para esta primera parte vamos a resolver los reactivos del 1 al 10.

¿Cómo resolver este simulacro de matemáticas?

Sigue estas recomendaciones para tener una mejor jornada de estudios:

1. Mide tu tiempo: Recuerda que tienes 4 horas para responder las 160 preguntas.
2. Toma notas: Apunta los ejercicios que más se te complican para repasarlos después.
3. Evita distracciones: Apaga tu celular, y pide que no te interrumpan mientras resuelves el simulacro.

Lo mejor es que intentes resolverlo por tu propia cuenta antes de consultar el procedimiento con el que llegamos a la respuesta correcta.

¿Es difícil la parte de matemáticas? Suele ser más complicada debido al extenso temario, matemáticas tiene 60 preguntas en el examen de la UABC. Con este simulador estudiarás los temas más resaltantes.

Hemos dividido el simulacro en tres partes, no deberías de tardar más de 1 hora en resolver los 30 ejercicios.

¿Cómo es el nuevo examen?

El nuevo examen de ingreso a la UABC consta de 160 reactivos, de los cuales 38 son ejercicios de prueba, mientras que los otros 122 serán los que valgan para tu puntuación final.

La prueba de ingreso abarca tres asignaturas, incluyendo matemáticas, y posee la siguiente estructura:

ÁREAS	PREGUNTAS
Lectura	36
Lengua Escrita	36
Matemáticas	50
Preguntas evaluativas	122
Preguntas piloto	38
TOTAL	160

Eliminando las preguntas piloto, la cantidad de reactivos por asignatura quedaría de la siguiente forma:

• Matemáticas: 50 reactivos
• Lectura: 36 reactivos
• Lengua escrita: 36 reactivos

Aunque individualmente matemáticas es la que tiene mayor cantidad de reactivos, español abarca más del 60% en el examen.

Temario de matemáticas

El temario de la UABC en matemáticas para 2023 tiene una forma particular para describir su contenido. En lugar de indicar puntualmente cada tema, la guía tiene una estructura por competencias.

Los ejercicios están orientados a que utilices determinadas herramientas matemáticas según el contexto del problema.

A continuación, el temario de matemáticas de la UABC:

Contenido	Reactivos
Herramientas Algebraicas: Resolución de problemas mediante el empleo de ecuaciones y sistemas lineales, ya sea a través de la representación de cantidades o de la representación gráfica	10
Problemas, Probabilidad y Análisis de Datos: Creación y análisis de relaciones, representación y análisis de datos cuantitativos y aplicación de probabilidades	15
Matemáticas Avanzadas: Creación de expresiones algebraicas y uso de gráficos que representan funciones exponenciales no lineales o cuadráticas	15
Temas Adicionales en Matemáticas: Solución de problemas asociados al área y volumen, aplicación de definiciones, teoremas sobre líneas, ángulos, triángulos y círculos	10
Total	50

1. Herramientas algebraicas.
   1. Planteamiento de una ecuación lineal con una variable mediante un contexto.
   2. Interpretación y solución de inecuaciones lineales con una variable.
   3. Construcción de una función lineal que represente la relación lineal entre dos variables.
   4. Interpretación y resolución de un sistema de ecuaciones lineales con tres variables.
   5. Interpretación y resolución de un sistema de ecuaciones lineales con dos variables.
   6. Resolución de ecuaciones lineales en una variable.
   7. Resolución de sistemas de ecuaciones lineales con dos variables.
   8. Interpretación de las características de una función lineal dentro de un contexto.
   9. Relación entre la representación gráfica y algebraica de una función lineal.
2. Problemas, probabilidad y análisis de datos.
   1. Resolución de problemas utilizando índices, tasas, relaciones proporcionales y dibujos a escalas mediante uno o varios pasos.
   2. Resolución de problemas utilizando porcentajes con uno o varios pasos.
   3. Resolución de problemas utilizando diferentes magnitudes, y diferentes sistemas de unidades.
   4. Análisis de variables involucradas en los diferentes modelos lineales, cuadráticos y exponenciales.
   5. Identificación de las características claves de un gráfico utilizando la relación entre las dos variables.
   6. Calcular frecuencias relativas y probabilidades (sumativa y multiplicativa).
   7. Realizar inferencias a partir de los datos de una muestra.
   8. Obtención de las medidas de tendencia central de datos y medidas de dispersión.
   9. Analizar reportes para hacer inferencias a partir de una tabla estadística.
3. Matemáticas avanzadas.
   1. Resolver problemas mediante funciones cuadráticas y exponenciales.
   2. Traducir contextos de lenguaje escrito a lenguaje algebraico.
   3. Convertir expresiones algebraicas con exponentes racionales a radicales y viceversa.
   4. Convertir ecuaciones de la forma ordinaria a la forma general y viceversa.
   5. Resolver ecuaciones cuadráticas.
   6. Simplificar operaciones aritméticas con polinomios.
   7. Resolver ecuaciones radicales y racionales en una variable.
   8. Resolución de un sistema de ecuaciones lineal y cuadrática.
   9. Simplificación de expresiones algebraicas (fracciones) complejas.
   10. Interpretación de parámetros, constantes o variables de una expresión no lineal en términos de un contexto dado.
   11. Comprensión y determinación de ceros y factores de polinomios para la elaboración de gráficos.
   12. Análisis de variables de expresiones algebraicas y su relación directa con el sistema de representación gráfico (sistemas de ecuaciones, descripción verbal del comportamiento gráfico, determinación de puntos importantes de una gráfica).
   13. Uso de notación de funciones e interpretación del significado de dichas notaciones (evaluación de funciones).
   14. Comprensión de las formas general, estándar o canónica de expresiones algebraicas para identificar parámetros de interés (vértice, ordenada en el origen).
4. Temas adicionales en matemáticas.
   1. Resolución de problemas que incluyan el cálculo de áreas o volúmenes de figuras geométricas.
   2. Uso de proporción trigonométrica y el Teorema de Pitágoras para resolver distintos problemas que consideran triángulos rectángulos.
   3. Resolución de triángulos oblicuángulos mediante ley de senos y ley de cosenos.
   4. Conversión entre grados y radianes y uso de radianes para determinar la longitud del arco; usar funciones trigonométricas en escala de radianes.
   5. Aplicación de teoremas sobre círculos para encontrar la longitud del arco, medidas de ángulos, longitud de la cuerda y áreas de un sector.
   6. Uso de conceptos y teoremas sobre congruencia y similitud para resolver problemas sobre líneas, ángulos y triángulos.
   7. Uso de la relación entre similitud, triángulo-rectángulo y proporciones trigonométricas; usar la relación entre seno y coseno de ángulos complementarios.
   8. Elaboración o uso de una ecuación en dos variables para resolver problemas sobre un círculo en un plano cartesiano.

Ejercicios de matemáticas resueltos

Recuerda revisar los requisitos de la convocatoria UABC 2023 para iniciar tu proceso de registro y prepárate para ingresar a uno de los 67 programas académicos de la Universidad Autónoma de Baja California.

Reactivo 1

En una empresa, laboran 150 personas en el Departamento de Recursos Humanos, 450 en Ventas, 200 en Administración, 100 en Área Contable y 900 en Producción. ¿Cuál de las siguientes afirmaciones es verdadera?

1. La minoría de los trabajadores labora en el Área Contable.
2. Un tercio de todos los empleados de la empresa, trabaja en Producción.
3. La mitad de todos los empleados de la empresa, trabaja en Contabilidad.
4. La mayoría de los trabajadores labora en Ventas.

Solución:

Para encontrar la respuesta correcta, vamos a examinar cada uno de los enunciados intentando comprobar la aseveración. Debido a que solo uno puede ser cierto, nos detendremos apenas verifiquemos cualquiera de ellos.

La minoría de los trabajadores labora en el área contable.

El área contable tiene 100 empleados y es la menor cantidad de entre todos los departamentos. Por lo tanto, la aseveración a) es correcta. Nos detenemos en este punto y concluimos que la respuesta correcta es el inciso a).

Reactivo 2

Simplifica la siguiente fracción algebraica:

\frac{{x}^{2}-3x+2}{{x}^{2}+x-2}

1. \frac{x-2}{x-1}
2. \frac{x+2}{x-1}
3. \frac{x-2}{x+2}
4. \frac{x+2}{x-2}

Solución:

Iniciamos factorizando a los trinomios del numerador y denominador. Recordemos que, cuando el coeficiente a=1 , podemos intentar factorizar buscando dos números que sumados sean iguales a b y que multiplicados, iguales a c .

Aplicamos el truco para el trinomio del numerador.

Dos números que sumados dan -3 y multiplicados +2 son: -1 y -2.

{x}^{2}-3x+2=\left(x-1\right)\left(x-2\right)

Factorizamos el trinomio del denominador.

Dos números que sumados dan +1 y multiplicados -2: +2 y -1.

{x}^{2}+x-2=\left(x+2\right)\left(x-1\right)

Sustituimos en la fracción original.

\frac{{x}^{2}-3x+2}{{x}^{2}+x-2}=\frac{\left(x-1\right)\left(x-2\right)}{\left(x+2\right)\left(x-1\right)}

Simplificamos a x-1 .

\frac{\left(x-1\right)\left(x-2\right)}{\left(x+2\right)\left(x-1\right)}=\frac{x-2}{x+2}

Concluimos el problema seleccionando como respuesta correcta al inciso c).

Reactivo 3

El largo de una mesa rectangular mide 8 pies más que su ancho, y el perímetro es de 56 pies. ¿Cuál es la ecuación que permite calcular las dimensiones de la mesa?

1. x\left(x+8\right)=56
2. x+x+8=56
3. 2x+2x+16=56
4. 2x+x+8=56

Solución:

El perímetro de cualquier polígono se calcula como la suma de todos sus lados. Para el caso de un rectángulo, tenemos dos aristas para el ancho, que llamaremos x y dos para el largo, que llamaremos y .

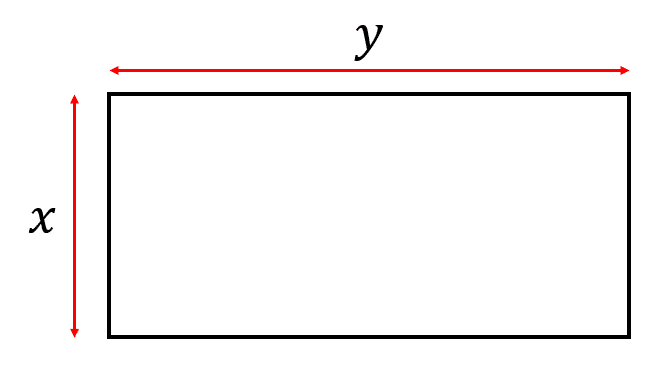
El enunciado nos dice que el largo y mide 8 pies más que el ancho x . Escrito en lenguaje algebraico quedaría:

y=x+8

Por otra parte, el perímetro de 56 pies es igual a la suma de dos veces el ancho más dos veces el largo.

56=2x+2y

Sustituimos a y por x+8 .

56=2x+2\left(x+8\right)\to 2x+2x+16=56

La ecuación que permite calcular las dimensiones de la mesa es:

2x+2x+16=56

La respuesta correcta es el inciso c).

Reactivo 4

¿Cuál es el resultado de transformar la siguiente expresión radical?

5(xyz{)}^{\frac{3}{4}}

1. \sqrt[4]{5{x}^{3}{y}^{3}{z}^{3}}
2. 5\sqrt[3]{{x}^{4}{y}^{4}{z}^{4}}
3. \sqrt[3]{5{x}^{4}{y}^{4}{z}^{4}}
4. 5\sqrt[4]{{x}^{3}{y}^{3}{z}^{3}}

Solución:

Para transformar la expresión del enunciado, empleamos la propiedad de la potencia fraccionaria.

{a}^{\frac{m}{n}}=\sqrt[n]{{a}^{m}}

El numerador de la fracción se convierte en la potencia y el denominador en el índice de la raíz.

5(xyz{)}^{\frac{3}{4}}=5\sqrt[4]{{\left(xyz\right)}^{3}}

Finalmente, deparamos el exponente para cada factor.

5\sqrt[4]{{\left(xyz\right)}^{3}}=5\sqrt[4]{{x}^{3}{y}^{3}{z}^{3}}

Comparando con los incisos, indicamos como respuesta correcta al inciso d).

Reactivo 5

Un vaso cónico de papel tiene una altura de 12 cm, y su diámetro máximo es de 8 cm. Si se llena de agua hasta 3 cuartas partes de su altura, ¿cuál es el diámetro del agua en la superficie?

1. 5.0 cm
2. 5.4 cm
3. 6.0 cm
4. 7.5 cm

Solución:

Antes de analizar el enunciado, hagamos una representación gráfica de la situación planteada.

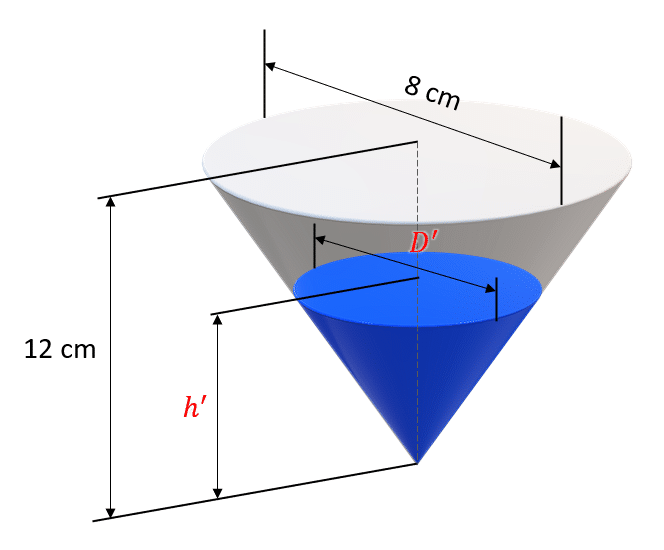
Debido a que se trata del mismo cono, solo que el nivel de agua disminuye de tal forma que {h}^{\text{'}} es igual a 3/4  partes de la altura nominal, podemos calcular el diámetro {D}^{\text{'}} aplicando semejanza de triángulos.

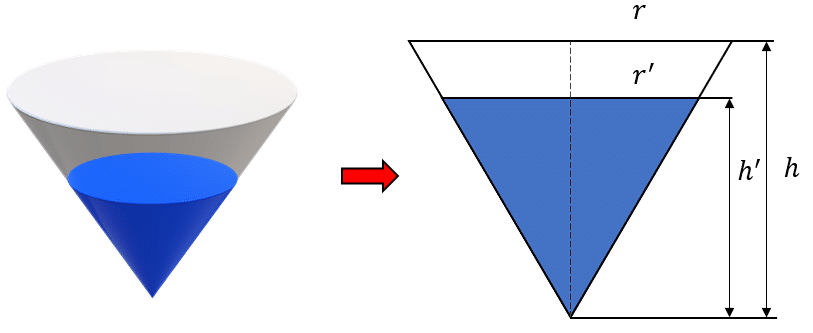
Aplicando semejanza nos queda:

\frac{r}{h}=\frac{{r}^{\text{'}}}{{h}^{\text{'}}}

Ahora, podemos sustituir el radio por su equivalencia con el diámetro.

r=\frac{D}{2}, {r}^{\text{'}}=\frac{{D}^{\text{'}}}{2}

Finalmente:

\frac{\frac{D}{2}}{h}=\frac{\frac{{D}^{\text{'}}}{2}}{{h}^{\text{'}}}\to \frac{D}{2h}=\frac{{D}^{\text{'}}}{2{h}^{\text{'}}}\to \frac{D}{h}=\frac{{D}^{\text{'}}}{{h}^{\text{'}}}

Sustituimos a {h}^{\text{'}} por \frac{3}{4}h .

\frac{D}{h}=\frac{{D}^{\text{'}}}{{h}^{\text{'}}}\to \frac{D}{h}=\frac{{D}^{\text{'}}}{\frac{3}{4}h}\to D=\frac{4}{3}{D}^{\text{'}}

Despejamos a {D}^{\text{'}} y calculamos su valor.

{D}^{\text{'}}=\frac{3}{4}D\to {D}^{\text{'}}=\frac{3}{4}\left(8\right)=6 \mathrm{c}\mathrm{m}

El diámetro es igual a 6 cm cuando la altura es 3 cuartos de la altura inicial.

La respuesta correcta es el inciso c).

Reactivo 6

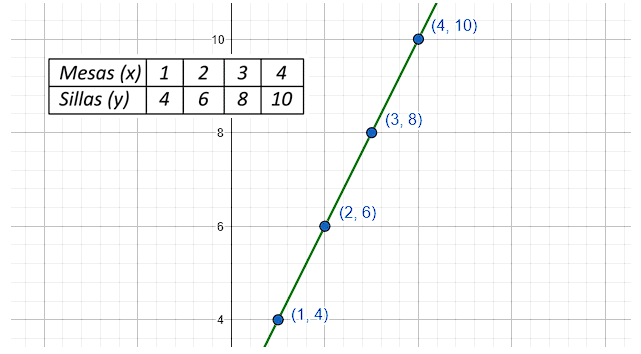
En una fiesta van a utilizar mesas y sillas. La disposición de estas se muestra en la siguiente tabla:

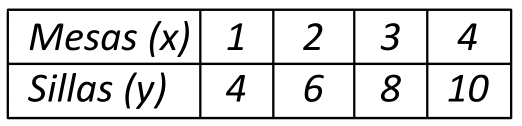
¿Cuál es el modelo matemático lineal que representa el comportamiento de la tabla anterior?

1. y=2x+6
2. y=2x+2
3. y=3x+1
4. y=6x-2

Solución:

Debemos analizar toda la información suministrada por el enunciado para que la solución del problema sea lo más rápida posible. A partir de la tabla, sabemos que la cantidad de mesas es la variable independiente x y que la cantidad de sillas es la variable dependiente y .

Por otra parte, los puntos representan una función lineal. Esto nos dice que la ecuación a utilizar debe ser la de una línea recta:

y-{y}_{o}=m\left(x-{x}_{o}\right)

Donde m es la pendiente que se puede calcular con 2 puntos cualesquiera extraídos de la tabla; mientras que \left({x}_{o}, {y}_{o}\right) es un punto que pertenece a la recta. Puedes elegir el que quieras, en esta ocasión usaremos \left({x}_{o}, {y}_{o}\right)=\left(1, 4\right) .

Cálculo de la pendiente.

m=\frac{{y}_{2}-{y}_{1}}{{x}_{2}-{x}_{1}}

Sustituimos \left({x}_{1}, {y}_{1}\right)=\left(1, 4\right) y \left({x}_{2}, {y}_{2}\right)=\left(2, 6\right) .

m=\frac{6-4}{2-1}=\frac{2}{1}=2

Evaluamos en la ecuación punto – pendiente a m y {P}_{o} .

y-4=2\left(x-1\right)\to y=2x+2

La función que representa a los puntos de la tabla es: y=2x+2 .

La respuesta correcta es el inciso b).

Reactivo 7

Un taxista tiene una tarifa de 11 pesos por banderazo y de 3 pesos por cada km recorrido. ¿Cuánto cobrará el taxista si recorre una distancia de 8 km?

1. 50 pesos
2. 54 pesos
3. 30 pesos
4. 35 pesos

Solución:

Nota: “banderazo” es el acto de “parar al taxi” para que nos preste su servicio.

Analizando el enunciado, sabemos que el precio a pagar por cualquier viaje viene dado por la suma del banderazo más el precio por kilómetro multiplicado por el recorrido del viaje.

\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{o}=11+3\cdot x

Donde x es la distancia recorrida por el taxista. Sustituimos el recorrido de 8 kilómetros.

\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{i}\mathrm{o}=11+\left(3\right)\left(8\right)=35 \mathrm{p}\mathrm{e}\mathrm{s}\mathrm{o}\mathrm{s}

La respuesta correcta es el inciso d).

Reactivo 8

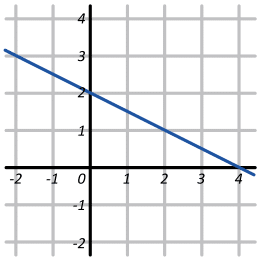
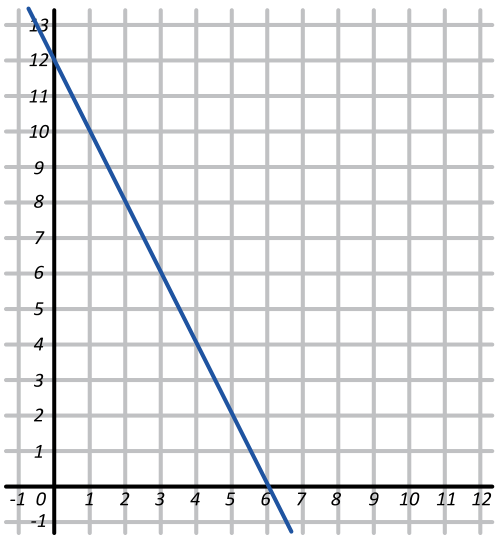
¿Cuál es la ecuación que se muestra en la gráfica?

1. y=2x+12
2. y=2x-12
3. y=-2x+12
4. y=-2x-12

Solución:

Examinando la figura, podemos asegurar desde el principio que la pendiente de la recta debe ser negativa, porque es oblicua hacia la izquierda. Por lo tanto, descartamos a los incisos a y b. Solo nos queda seleccionar la respuesta correcta entre c y d.

Ya que la recta pasa por el punto \left(6, 0\right) , podemos sustituir en ambas ecuaciones x=6 y la que arroje como resultado y=0 será la respuesta correcta.

Ecuación del inciso c.

y=-2\left(6\right)+12=-12+12=0

La recta que representa a la función del gráfico se encuentra en el inciso c). Otra forma de resolver el ejercicio, sería empleando la forma simétrica de la recta:

\frac{x}{a}+\frac{y}{b}=1

Donde a y b son los cortes con los ejes x y y respectivamente. Para efectos de este problema: a=6 y b=12 .

\frac{x}{6}+\frac{y}{12}=1

Despejamos a y .

\frac{y}{12}=1-\frac{x}{6}\to y=12-2x

\therefore y=-2x+12

Reactivo 9

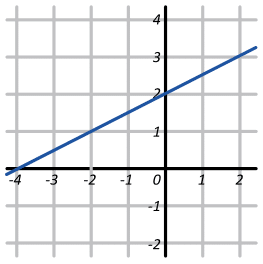
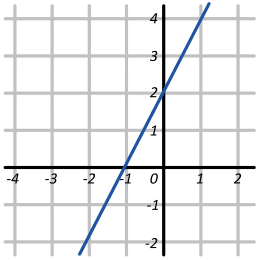
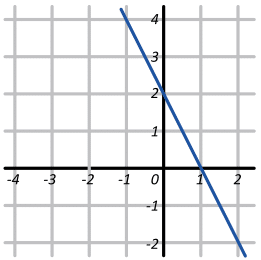
Encuentra una gráfica de una línea recta perpendicular, cuya pendiente es de ½ y ordenada en el origen es de 2.

1. 
2. 
3. 
4. 

Solución:

El enunciado nos dice que la pendiente m de la recta debe ser igual a +\frac{1}{2} y, que el corte con el eje vertical debe ser igual a 2. Examinando a los incisos, todos cortan al eje y en 2, por lo que este dato no es crítico para la solución.

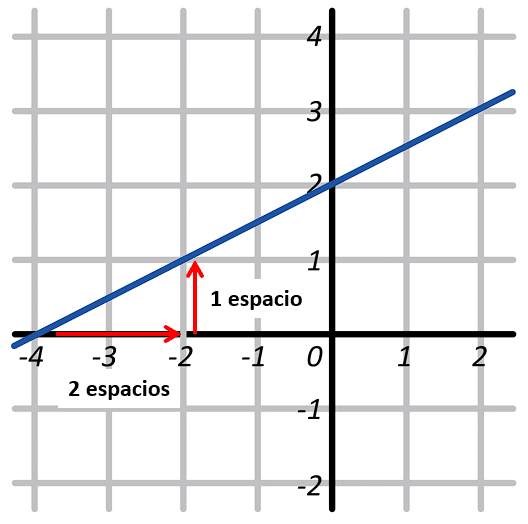
Por otra parte, la pendiente debe ser positiva. Solo poseen pendiente positiva los incisos b y c. La pendiente de 1/2 significa que: al recorrer 2 espacios en sentido horizontal, solo avanzamos 1 espacio en sentido vertical.

La gráfica que cumple con esto entre b y c, es la del inciso b).

La respuesta correcta es la opción b).

Reactivo 10

La temperatura de un envase de vidrio se puede obtener con la siguiente función lineal: 6A – 2B +4 = 0.

Donde A es el tiempo transcurrido y B es la temperatura del envase. ¿Cuál es la razón del cambio entre la temperatura del envase y el tiempo?

1. -2
2. 3
3. 4
4. 6

Solución:

Cuando tratamos con problemas que muestran modelos matemáticos, el tiempo siempre es la variable independiente, por consecuencia, la temperatura del envase B es la variable dependiente.

Teniendo en cuenta que se trata de una función lineal, la razón de cambio entre la temperatura del envase respecto del tiempo, es igual a la pendiente de la recta. Despejamos a B para encontrar la pendiente.

6A-2B+4=0

-2B=-6A-4

B=3A+2

La pendiente o razón de cambio de la temperatura del envase respecto del tiempo es igual a 3.

La respuesta correcta es el inciso b).