¡Felicidades, aspirante! Llegamos a la tercera y última parte del simulador de matemáticas del nuevo ExIES, desde el reactivo 21 hasta el 30, como preparación al examen de ingreso de la UABC.

Reactivo 21
Convierte 80° a radianes.
- \frac{3\pi }{9}
- \frac{4\pi }{9}
- \frac{6\pi }{9}
- \frac{8\pi }{9}
Solución:
Para convertir un ángulo de grados a radianes, utilizamos la siguiente ecuación:
{\theta }_{r}=\frac{\pi }{180°}{\theta }_{°}
Sustituimos {\theta }_{°}=80° .
{\theta }_{r}=\frac{\pi }{180°}\left(80°\right)=\frac{4\pi }{9}
Escogemos como respuesta correcta al inciso b).
Reactivo 22
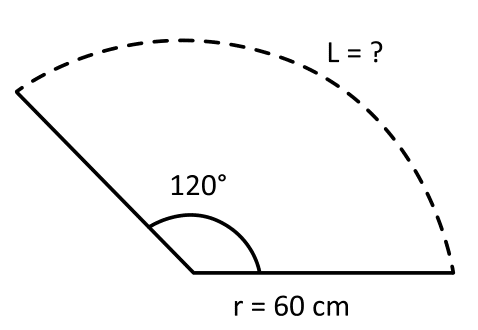
Si el valor del radio es igual a 60 cm, ¿cuál es la longitud del arco L?
- 10\pi \mathrm{c}\mathrm{m}
- 20\pi \mathrm{c}\mathrm{m}
- 30\pi \mathrm{c}\mathrm{m}
- 40\pi \mathrm{c}\mathrm{m}
Solución:
Empleamos la fórmula para calcular el arco de circunferencia.
l=\theta r
El ángulo \theta se debe sustituir en radianes. Convertimos los 120° a radianes.
{\theta }_{r}=\frac{\pi }{180}\left(120\right)=\frac{2\pi }{3}
Finalmente, sustituimos en la ecuación:
l=\left(\frac{2\pi }{3}\right)\left(60\right)=40\pi \mathrm{c}\mathrm{m}
La respuesta correcta es el inciso d).
Reactivo 23
Una circunferencia con centro fuera del origen tiene como ecuación:
{\left(x-2\right)}^{2}+{\left(y+3\right)}^{2}=25
¿Cuál es su ecuación en forma general?
- {x}^{2}+{y}^{2}-4x+6y-12=0
- {x}^{2}+{y}^{2}-4x+6y+15=0
- {x}^{2}+{y}^{2}-2x+3y+12=0
- {x}^{2}+{y}^{2}+4x+6y+12=0
Solución:
Para dar con la forma general de la circunferencia, debemos desarrollar los binomios al cuadrado aplicando el producto notable correspondiente.
Desarrollamos a {\left(x-2\right)}^{2} .
{\left(x-2\right)}^{2}+{\left(y+3\right)}^{2}=25\to {x}^{2}-4x+4+{\left(y+3\right)}^{2}=25
Desarrollamos a {\left(y+3\right)}^{2} .
{x}^{2}-4x+4+{\left(y+3\right)}^{2}=25\to {x}^{2}-4x+4+{y}^{2}+6y+9=25
Agrupamos y simplificamos.
{x}^{2}+{y}^{2}-4x+6y+13-25=0
{x}^{2}+{y}^{2}-4x+6y-12=0
Comparando con los incisos, concluimos que la respuesta correcta es el inciso a).
Reactivo 24
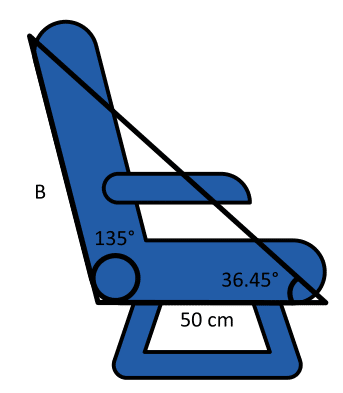
Un pasajero en vuelo comercial, inclina su asiento hacia atrás, formando un ángulo de 135°. ¿Qué modelo matemático, permite calcular la longitud de la parte reclinable del asiento?
- \frac{50}{\mathrm{sin}\left(36.45°\right)}=\frac{B}{\mathrm{sin}\left(135°\right)}
- \frac{50}{\mathrm{sin}\left(180-135-36.45°\right)}=\frac{B}{\mathrm{sin}\left(135°\right)}
- \frac{50}{\mathrm{sin}\left(180-135-36.45°\right)}=\frac{B}{\mathrm{sin}\left(36.45°\right)}
- \frac{50}{\mathrm{sin}\left(135°\right)}=\frac{B}{\mathrm{sin}\left(36.45°\right)}
Solución:
Para resolver este triángulo obtusángulo, debemos utilizar la ley del seno o la ley del coseno. Debido a que conocemos un lado y dos ángulos, nos conviene emplear la ley del seno en este caso.
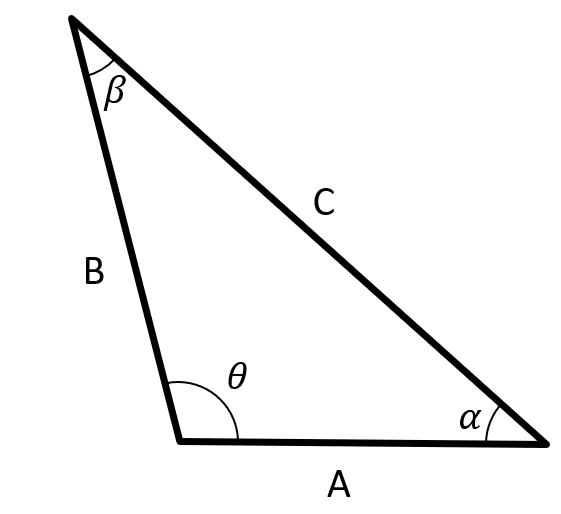
\frac{A}{\mathrm{sin}\beta }=\frac{B}{\mathrm{sin}\alpha }=\frac{C}{\mathrm{sin}\theta }
Aplicando la ley del al triángulo nos queda:
\frac{50}{\mathrm{sin}\beta }=\frac{B}{\mathrm{sin}36.45°}
El ángulo \beta se puede calcular aplicando la propiedad de la suma de ángulos internos.
180°=36.45+135+\beta
\therefore \beta =180-135-36.45
Sustituimos.
\frac{50}{\mathrm{sin}\left(180-135-36.45\right)}=\frac{B}{\mathrm{sin}36.45°}
La respuesta correcta es el inciso c).
Reactivo 25
En el departamento de Recursos Humanos de un supermercado se tiene la siguiente información de sus trabajadores:
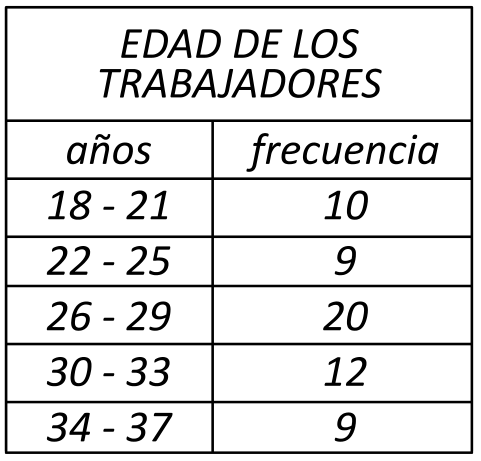
¿Cuál es la frecuencia relativa correspondiente a los trabajadores que están entre los 26 y 29 años de edad?
- 0.1500
- 0.1666
- 0.2000
- 0.3333
Solución:
La frecuencia relativa se calcula como el cociente entre la frecuencia absoluta de la clase y el total de datos. Examinando la tabla:
{F}_{26-29}=20, N=60
Finalmente:
{f}_{26-29}=\frac{20}{60}=\frac{1}{3}=0.3333
La respuesta correcta es el inciso d).
Reactivo 26
A partir de los siguientes datos: 8, 6, 4, 8, 7.
¿Cuál es el valor de la media aritmética \stackrel{-}{x} y la desviación estándar S?
- \stackrel{-}{x}=0.6;S=12
- \stackrel{-}{x}=6.6;S=1.5
- \stackrel{-}{x}=33;S=64
- \stackrel{-}{x}=66;S=12
Solución:
Este reactivo puede resolverse de forma rápida con sólo calcular la media. Llegamos a esta conclusión, porque las medias en los incisos son todas distintas entre ellas.
Cálculo de la media
\stackrel{-}{x}=\frac{8+6+4+8+7}{5}=\frac{33}{5}=6.6
La media del conjunto de datos es 6.6, el único inciso que tiene como media este valor es el b). Indicamos a la opción b) como la respuesta correcta.
Reactivo 27
Un estacionamiento del centro de la ciudad cobra $8.00 por la primera hora y $5.00 pesos por cada hora adicional, ¿cuál es la inecuación que permite calcular el tiempo máximo que puede estacionar su auto si no desea pagar más de $38.00?
- 8+3x\ge 38
- 8x+5\ge 38
- 8+5x\le 38
- 8x+5\le 38
Solución:
Debido a que el pago máximo es de 38 pesos, damos por sentado que el usuario se va a quedar más de una hora en el estacionamiento. Por lo tanto, la expresión 8+5x nos permite calcular el monto a pagar cuando el usuario se queda por más de una hora en el estacionamiento.
Teniendo en cuenta que no desea pagar más de 38 pesos, la expresión anterior debe ser menor o igual que 38 pesos.
8+5x\le 38
La inecuación que permite calcular el tiempo máximo para no pagar más de 38 pesos, se encuentra en el inciso c).
Reactivo 28
Un papá y su hijo salen a correr todos los fines de semana al deportivo. Si se sabe que seis veces el recorrido del papá, más cinco veces el recorrido del hijo es igual a 63 vueltas, y que tres veces el recorrido del papá es igual al recorrido del hijo más 21, ¿cuántas vueltas da el hijo?
- 3 vueltas
- 7 vueltas
- 9 vueltas
- 15 vueltas
Solución:
El enunciado nos entrega las relaciones entre las variables como un sistema de ecuaciones, expresado en lenguaje natural. Iniciamos expresando todo como fórmula algebraica. El recorrido del papa será p y el del hijo h .
…seis veces el recorrido del papá, más cinco veces el recorrido del hijo es igual a 63 vueltas…
6p+5h=63
…tres veces el recorrido del papá es igual al recorrido del hijo más 21…
3p=h+21\to 3p-h=21
El sistema de ecuaciones quedaría:
\left\{\begin{array}{c}6p+5h=63\\ 3p-h=21\end{array}\right.
Multiplicamos la segunda ecuación por -2 para eliminar las vueltas del padre.
\left\{\begin{array}{c}6p+5h=63\\ -6p+2h=-42\end{array}\right.
7h=21\to h=3
El hijo da un total de 3 vueltas.
La respuesta correcta es el inciso a).
Reactivo 29
Determina el valor de x. Considera que los triángulos son congruentes.
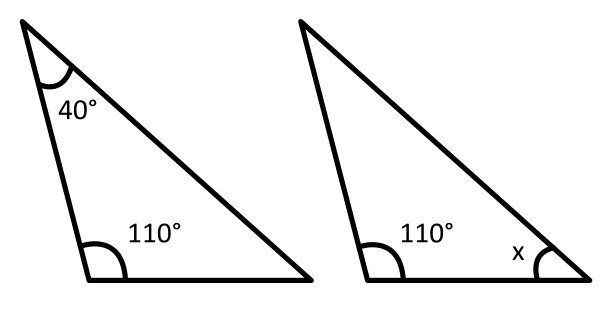
- 20°
- 30°
- 40°
- 90°
Solución:
Cuando dos figuras geométricas (no sólo triángulos) son congruentes, significa que tienen el mismo tamaño y forma, pero se encuentran en posiciones y rotaciones distintas.
Teniendo en cuenta esto y examinando a los triángulos de la imagen, el ángulo desconocido x en el segundo triángulo, es el mismo para el primer triángulo.
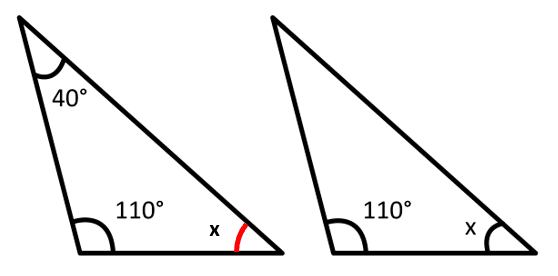
Ahora, aplicamos la propiedad de la suma de los ángulos internos del triángulo.
180=40+110+x\to x=180-110-40
\therefore x=30°
La respuesta correcta es el inciso b).
Reactivo 30
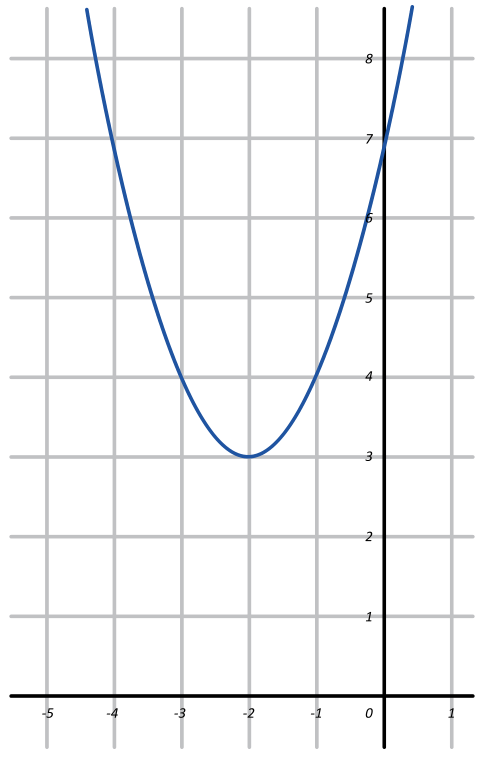
Encuentra la ecuación que describa el comportamiento de la gráfica mostrada, a continuación:
- y={\left(x+2\right)}^{2}+3
- y={\left(x+2\right)}^{2}-3
- y={\left(x-2\right)}^{2}+3
- y={\left(x-2\right)}^{2}-3
Solución:
Examinando la gráfica del enunciado, podemos identificar 3 cosas importantes: que es una parábola con eje focal vertical, que abre hacia arriba y que tiene el vértice en \left(-2, 3\right) . La ecuación ordinaria de una parábola vertical es:
{\left(x-h\right)}^{2}=4p\left(y-k\right)
Sustituimos el valor del vértice.
{\left(x+2\right)}^{2}=4p\left(y-3\right)
Descartamos a los incisos c y d, porque el término con x tiene al 2 negativo y no positivo. Para determinar el parámetro 4p , sustituimos cualquier punto que pertenezca a la parábola. A partir de la gráfica seleccionamos \left(0, 7\right) .
4p=\frac{{\left(0+2\right)}^{2}}{\left(7-3\right)}=\frac{4}{4}=1
Finalmente:
{\left(x+2\right)}^{2}=y-3\to y={\left(x+2\right)}^{2}+3
Comparando con los incisos, concluimos que la respuesta correcta es el inciso a).

