En este examen simulacro resolveremos 24 reactivos del área 2 de la parte de matemáticas con los temas de la guía oficial de la UNAM, con el objetivo de que pongas a prueba tus conocimientos antes de presentar el examen de admisión a la UNAM.

El área 2 (ciencias biológicas, químicas y de la salud) de la UNAM corresponde en su mayoría a las carreras de ciencias de la salud, en esta área encontrarás la carrera más difícil, por su puesto nos referimos a medicina en la UNAM.
Estructura examen área 2
El examen de ingreso a la UNAM tiene un total de 120 reactivos, y un tiempo de 3 horas pares responderles (es importante tomar en cuenta el tiempo).
Conoce el temario completo del examen de la UNAM de la guía oficial
El área 2 tiene 9 materias, de las cuales la que mayor peso tiene es la de matemáticas con 24 reactivos, es importante mencionar que entre química y biología suman 26 de los 120 problemas del examen.
Estructura examen de la UNAM para el área 2
| Materia | Reactivos |
| Español | 18 |
| Matemáticas | 24 |
| Física | 12 |
| Química | 13 |
| Biología | 13 |
| Historia universal | 10 |
| Historia de México | 10 |
| Literatura | 10 |
| Geografía | 10 |
| Total | 120 |
Temario matemáticas UNAM área 2
El Área 1 (ciencias biológicas, químicas y de la salud) incluye cálculo diferencial e integral. Si no sabes los pasos para registrarte al proceso de admisión te recomiendo que consultes la convocatoria UNAM.
Estos son los temas que tienes que estudiar:
- Operaciones con números reales, complejos y expresiones algebraicas
- Números reales
- Suma y resta
- Multiplicación y división
- Raíces y potencias con exponente racional
- Números complejos
- Suma y resta
- Multiplicación
- Expresiones algebraicas
- Suma y resta
- Multiplicación y división
- Raíces y potencias con exponente racional
- Operaciones con radicales
- Números reales
- Productos notables y factorización
- Binomio de Newton a+bn, n ∈N
- Teorema del residuo y del factor
- Simplificación de fracciones algebraicas
- Operaciones con fracciones algebraicas
- Ecuaciones
- Ecuación, identidad y propiedades de la igualdad
- Ecuaciones de primer grado
- Ecuaciones de segundo grado
- Desigualdades
- Desigualdad de primer grado en una variable y sus propiedades
- Sistemas de ecuaciones
- Sistemas de dos ecuaciones lineales con dos incógnitas
- Métodos de solución
- Sistemas de tres ecuaciones lineales con tres incógnitas
- Métodos de solución (Regla de Cramer)
- Sistemas de dos ecuaciones lineales con dos incógnitas
- Funciones algebraicas
- Dominio, contradominio y regla de correspondencia
- Rango o imagen
- Gráfica
- Implícitas y explícitas
- Crecientes y decrecientes
- Continuas y discontinuas
- Álgebra de funciones
- Trigonometría
- Trigonometría básica
- Medida de un ángulo (conversión de grados a radianes y de radianes a grados)
- Razones trigonométricas
- Resolución de triángulos rectángulos
- Ley de los Senos y Ley de los Cosenos
- Resolución de triángulos oblicuángulos
- Razones trigonométricas para un ángulo en cualquier cuadrante. Fórmulas de reducción
- Funciones trigonométricas
- El círculo trigonométrico
- Funciones trigonométricas directas
- Dominio y rango
- Periodo y amplitud
- Desfasamiento
- Asíntotas de la gráfica
- Trigonometría básica
- Funciones exponenciales y logarítmicas
- Dominio y rango
- Gráficas y asíntotas
- Recta
- Distancia entre dos puntos
- Coordenadas de un punto que divide a un segmento de acuerdo con una razón dada
- Pendiente de una recta
- Formas de la ecuación de la recta y su gráfica
- Condiciones de paralelismo y perpendicularidad
- Distancia de un punto a una recta
- Ecuaciones de las medianas, mediatrices y alturas de un triángulo. Puntos de intersección (ortocentro, circuncentro y baricentro)
- Circunferencia
- Circunferencia como lugar geométrico
- Formas ordinarias (canónica) y general de la ecuación de la circunferencia con centro en el origen
- Ecuación de la circunferencia con centro en (h, k) en las formas ordinaria y general
- Elementos de una circunferencia
- Parábola
- Parábola como lugar geométrico
- Formas ordinaria y general de la ecuación de la parábola cuando el vértice está en el origen y el eje focal coincide con alguno de los ejes coordenados
- Formas ordinaria y general de la ecuación de la parábola cuando el vértice está en un punto cualquiera del plano y eje focal paralelo a alguno de los ejes coordenados
- Elementos de una parábola
- Elipse
- Elipse como lugar geométrico
- Relación entre los parámetros a, b y c
- Formas ordinaria y general de la ecuación de la elipse con centro en el origen y eje focal sobre alguno de los ejes coordenados
- Formas ordinaria y general de la ecuación de la elipse con centro fuera del origen y eje focal paralelo a alguno de los ejes coordenados
- Elementos de una elipse
- Hipérbola
- Hipérbola como lugar geométrico
- Relación entre los parámetros de la hipérbola a, b y c
- Formas ordinaria y general de la ecuación de la hipérbola con centro en el origen y eje focal sobre alguno de los ejes coordenados
- Formas ordinaria y general de la ecuación de la hipérbola con centro fuera del origen y eje focal paralelo a alguno de los ejes coordenados
- Elementos de una hipérbola
- Ecuación general de segundo grado
- Las cónicas
- Ecuación general de segundo grado
- Criterios para identificar a la cónica que representa una ecuación de segundo grado
- Traslación de ejes
- Límites
- Concepto intuitivo
- Definición formal
- Teoremas sobre límites
- Obtención de límites
- Formas indeterminadas
- Continuidad en un punto y en un intervalo
- La derivada
- Definición de derivada y sus notaciones
- Obtención de derivadas
- Reglas de la cadena
- Derivada de funciones implícitas
- Derivadas sucesivas de una función
- Interpretación geométrica y física
- Ecuaciones de la tangente y de la normal a una curva
- Cálculo de velocidad y aceleración de un móvil
- Maximino y mínimos relativos de una función
- Máximos y mínimos absolutos en un intervalo cerrado
- Puntos de inflexión y de concavidad de una curva
- Problemas de la vida cotidiana
- La integral
- Función integrable en un intervalo cerrado
- Teoremas que justifican las propiedades de la integral de una función
- Integral inmediata
- Tabla de fórmulas de integración
- Métodos de integración
- Integral definida y su notación
Recomendaciones para resolver este simulacro
Primero que nada intenta resolver cada ejercicio por tu parte, es importante que identifiques los temas que más se te compliquen y profundices en ellos una vez que termines este examen.
Conoce los aciertos necesarios por carrera para ingresar a la UNAM.
Algunas recomendaciones antes de comenzar:
- Usa un cronómetro para medir tu tiempo.
- Evita distracciones.
- Anota los temas que más se te complican.
- Revisa los pasos, y analiza en que fallaste en caso de que no lo puedas resolver.
Además de explicar los ejercicios paso a paso, hemos indicado el tema al que pertenecen.
Reactivo 1: Proporciones y fracciones
Un virus informático atacó el disco duro de una computadora, el primer día destruyó dos terceras partes del disco duro; el segundo día destruyó una cuarta parte de lo que quedó; finalmente, al tercer día destruyó la quinta parte de lo restante. ¿Qué fracción del disco duro quedó sin dañar?
- \frac{13}{60}
- \frac{3}{60}
- \frac{1}{5}
- \frac{1}{8}
Solución:
Antes de ser atacado por el virus, el disco duro se encontraba al 100%, en proporción esto corresponde a 1.

Durante el primer día, se perdieron dos terceras partes \frac{2}{3} del disco, es decir, la porción en buen estado se redujo a 1-\frac{2}{3}=\frac{1}{3} .
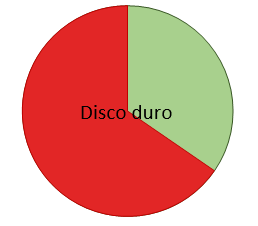
El segundo día destruyó una cuarta parte \frac{1}{4} de lo que quedó, es decir, debemos restar la cuarta parte de la capacidad restante \frac{1}{3}*\frac{1}{4}=\frac{1}{12} a dicha capacidad restante:
\frac{1}{3}-\frac{1}{12}=\frac{1}{4}
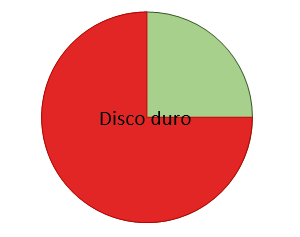
Finalmente, para el tercer día el virus consumió una quinta parte \frac{1}{5} del restante \frac{1}{4}*\frac{1}{5}=\frac{1}{20} , para saber cuánto quedó le debemos restar \frac{1}{20} a \frac{1}{4} .
\frac{1}{4}-\frac{1}{20}=\frac{1}{5}
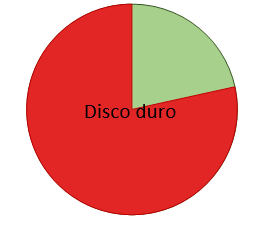
Concluimos indicando que al disco duro le quedó una \frac{1}{5} parte sin dañar.
Comparando con las opciones, escogemos a la C como respuesta correcta.
Reactivo 2: Expresiones racionales
Simplifica la siguiente fracción.
\frac{-{x}^{2}-3x+40}{x+8}
- x-5
- -x+5
- -x+8
- x-8
Solución:
Para encontrar la forma simplificada de la expresión, debemos representar al trinomio del numerador como el producto de sus factores primos, es decir, factorizar el trinomio cuadrado.
Extraemos factor común el signo menos.
\frac{-{x}^{2}-3x+40}{x+8}=-\frac{{x}^{2}+3x-40}{x+8}
Existen diferentes maneras para factorizar el trinomio, en este caso intentaremos encontrar dos números que multiplicados sean -40 y sumados 3, dichas cantidades son 8 y -5.
8*-5=40
8+\left(-5\right)=8-5=3
Reescribimos el trinomio.
-\frac{{x}^{2}+3x-40}{x+8}=-\frac{\left(x-5\right)\left(x+8\right)}{x+8}
Ahora, vemos que se simplifican los monomios x+8 presentes en el numerador y el denominador.
-\frac{\left(x-5\right)\left(x+8\right)}{x+8}=-\left(x-5\right)
Distribuimos el signo menos.
-\left(x-5\right)=-x+5
Indicamos finalmente que:
\frac{-{x}^{2}-3x+40}{x+8}=-x+5
Examinando las opciones que ofrece el problema, escogemos como correcta la B.
Reactivo 3: Ecuaciones e identidades
Selecciona la expresión que corresponde a una ecuación.
- \mathrm{sin}\left(x\right)=\frac{1}{2}
- \mathrm{sin}\left(x\right)=\frac{1}{2}x
- {\mathrm{sin}}^{2}\left(x\right)+{\mathrm{cos}}^{2}\left(x\right) =1
- {\mathrm{sec}}^{2}\left(x\right) -{\mathrm{tan}}^{2}\left(x\right) =1
Solución:
En este caso, debemos saber diferenciar entre ecuación e identidad. Ambas están conformadas por dos miembros y un signo de igualdad pero, la ecuación solo se cumple para ciertos valores de la variable y la identidad se cumple para todos sus posibles valores.
De entre los incisos, la única que cumple con esta condición es el inciso A, porque el seno de x valdrá \frac{1}{2} para ciertos valores de su argumento. Por otro lado C y D, son la identidad Pitagórica en términos de seno y coseno, y de tangente con secante, respectivamente.
El inciso B es una ecuación trascendental con dos posibles soluciones y podría, al igual que la opción A, ser la respuesta correcta. Teniendo en cuenta todo este análisis, seleccionamos como correcta a la opción A y a la B.
Reactivo 4: Ecuación racional
La solución de la ecuación \frac{x}{3}-\frac{x-5}{4}=2 es:
- 8
- 9
- 10
- 7
Solución:
Podemos seguir distintos caminos para resolver la ecuación: extraer factor común, desarrollar la suma de fracciones o deshacer los denominadores; en esta ocasión optamos por esa última vía.
Multiplicamos por 3 y luego por 4 toda la expresión.
\frac{x}{3}-\frac{x-5}{4}=2\to x-\frac{3\left(x-5\right)}{4}=6
Ahora por 4.
x-\frac{3\left(x-5\right)}{4}=6\to 4x-3\left(x-5\right)=24
Aplicamos distributiva donde haga falta.
4x-3x+15=24
Simplificamos y despejamos.
x=24-15
\therefore x=9
La solución a la ecuación \frac{x}{3}-\frac{x-5}{4}=2 es x=9 .
Concluimos seleccionando la B como respuesta correcta.
Reactivo 5: Desigualdades lineales
La solución de la desigualdad 3x-5>x+6 es:
- x>\frac{11}{2}
- x>-\frac{11}{2}
- x>\frac{2}{11}
- x>-\frac{2}{11}
Solución:
Para resolver inecuaciones lineales, debemos aplicar las propiedades de las desigualdades: suma resta, producto y cociente de cantidades; hasta dejar sola (en el primer miembro) a la variable.
3x-5>x+6
Restamos de ambos lados x .
3x-5-x>x+6-x\to 3x-x-5>6
2x-5>6
Ahora, sumamos 5.
2x-5+5>6+5\to 2x>11
Por último, dividimos por 2. Ya que es positivo, la dirección de la desigualdad se mantiene.
\frac{2x}{2}>\frac{11}{2}\to x>\frac{11}{2}
Finalmente, la solución de la desigualdad 3x-5>x+6 es x>\frac{11}{2} .
Concluimos indicando como respuesta correcta la opción A.
Reactivo 6: Sistema de ecuaciones lineales
Soluciona el sistema de ecuaciones
\left\{\begin{array}{c}5x+2y-z=-7\\ x-2y+2z=0\\ 3y+z=17\end{array}\right.
- x=-2,y=3,z=5
- x=2,y=4,z=-5
- x=-2,y=4,z=5
- x=2,y=3,z=-5
Solución:
Para resolver el sistema de ecuaciones 3×3 del enunciado, podemos recurrir a los métodos: por sustitución, por igualación, por reducción o emplear la regla de Cramer.
En esa ocasión, emplearemos sustitución. Despejamos a z de la tercera ecuación, el resultado lo reemplazamos en 1 y 2 para obtener un sistema 2×2 más chico.
Despejando a z .
3y+z=17\to z=17-3y
Sustituyendo en 1.
5x+2y-\left(17-3y\right)=-7
5x+2y-17+3y=-7
5x+5y=17-7
5x+5y=10
Dividimos entre 5.
x+y=2
Sustituyendo z en 2.
x-2y+2\left(17-3y\right)=0
x-2y+34-6y=0
x-8y=-34
Nuevo sistema:
\left\{\begin{array}{c}x+y=2\\ x-8y=-34\end{array}\right.
Despejamos a x de x+y=2 .
x+y=2\to x=2-y
Sustituimos en x-8y=-34 .
2-y-8y=-34
-9y=-36
\therefore y=4
Sustituimos este resultado en x=2-y .
x=2-4=-2
\therefore x=-2
Por último, para obtener a z sustituimos el valor de y en z=17-3y .
z=17-3\left(4\right)=5
\therefore z=5
La solución al SEL es:
x=-2;y=4;z=5
Comparando con los incisos, la respuesta correcta es la C.
Reactivo 7: Dominio de una función real
Encuentra el dominio de la función que tiene regla de correspondencia f\left(x\right)={x}^{2}+1 y rango {R}_{f}=\forall f\left(x\right)\in \left[\mathrm{1,17}\right]
- {D}_{f}=[-\mathrm{4,4})
- {D}_{f}=(-\mathrm{4,4}]
- {D}_{f}=\left(-\mathrm{4,4}\right)
- {D}_{f}=\left[-\mathrm{4,4}\right]
Solución:
El problema solicita hallar el dominio de una función y para ello, nos da la regla de correspondencia entre el dominio y el rango: f\left(x\right)={x}^{2}+1 y el rango de la función.
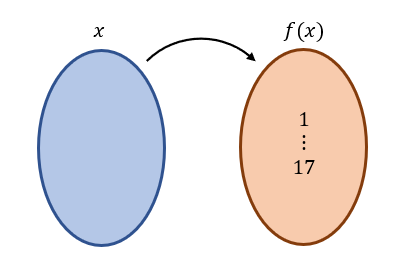
Necesitamos los valores que deben ir en el conjunto de las x para obtener como resultado los valores del conjunto de las imágenes f\left(x\right) . Ya que la función es cuadrática, para un mismo valor del rango existen dos valores del dominio. Esto se ve con más claridad si encontramos la inversa de f .
x=\pm \sqrt{f\left(x\right)-1}
El conjunto dominio de f es la unión de los resultados para {x}_{+}=\sqrt{f\left(x\right)-1} y para {x}_{-}=-\sqrt{f\left(x\right)-1} .
Dom\left\{f\left(x\right)\right\}=\forall x\in \left\{{x}_{+}\right\}\cup \left\{{x}_{-}\right\}
No es necesario sustituir todos los números en el intervalo de 1 a 17, solo los extremos.
Para {x}_{+}=\sqrt{f\left(x\right)-1} :
f\left(x\right)=1\to {x}_{+}=\sqrt{1-1}=0
f\left(x\right)=17\to {x}_{+}=\sqrt{17-1}=4
\left\{{x}_{+}\right\}=\left[\mathrm{0,4}\right]
Para {x}_{-}=-\sqrt{f\left(x\right)-1} :
f\left(x\right)=1\to {x}_{-}=-\sqrt{1-1}=0
f\left(x\right)=17\to {x}_{-}=-\sqrt{17-1}=-4
\left\{{x}_{-}\right\}=\left[-\mathrm{4,0}\right]
Unimos ambas soluciones:
Dom\left\{f\left(x\right)\right\}=\forall x\in \left\{{x}_{+}\right\}\cup \left\{{x}_{-}\right\}=\forall x\in \left[\mathrm{0,4}\right]\cup \left[-\mathrm{4,0}\right]=\forall x\in \left[-\mathrm{4,4}\right]
Finalmente.
{D}_{f}=\left[-\mathrm{4,4}\right]
Finalizamos seleccionando como respuesta correcta la opción D.
Lista completa de carreras ofertadas por la UNAM
Reactivo 8: Trigonometría
En un triángulo rectángulo, la hipotenusa mide 10 unidades y uno de sus ángulos es de 30°. ¿Cuántas unidades mide el lado opuesto al ángulo dado?
- 6
- \frac{1}{20}
- 5
- \frac{15}{\sqrt{3}}
Solución:
Para visualizar con mayor facilidad lo que solicita el problema, haremos un pequeño bosquejo del triángulo rectángulo.
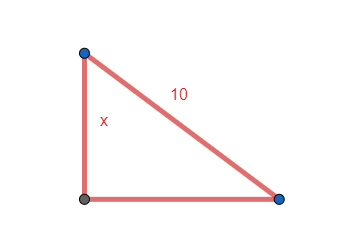
La hipotenusa vale 10 unidades, el ángulo de 30 grados entre la hipotenusa y uno de los catetos y x que representa al cateto cuya magnitud es desconocida. Para calcularlo, solo debemos recurrir al seno de 30 grados.
\sin 30 =\frac{CO}{H}=\frac{x}{10}
Despejamos.
x=10\sin 30 =10*\frac{1}{2}=5
El cateto opuesto al ángulo de 30 grados mide 5 unidades.
Comparando con las opciones del problema, la respuesta correcta es la C.
Reactivo 9: Trigonometría
En un triángulo rectángulo, la hipotenusa mide 6 unidades y uno de sus ángulos es de 30°. ¿Cuántas unidades mide el lado opuesto al ángulo dado?
- 3\sqrt{3}
- 2
- 3
- 2\sqrt{3}
Solución:
Similar al reactivo anterior, realizaremos un dibujo del triángulo planteado por el problema. Ten en cuenta que es indistinto el careto que se escoja, siempre que sea opuesto al ángulo de 30°.
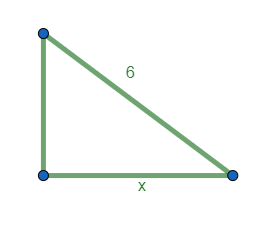
La hipotenusa vale 6 unidades, el ángulo de 30 grados se encuentra entre la hipotenusa y el otro cateto y x que representa al cateto que debemos calcular. Empleamos la identidad trigonométrica seno que relaciona la hipotenusa, un ángulo y al cateto opuesto a él.
\sin 30 =\frac{CO}{H}=\frac{x}{6}
Despejamos.
x=6\sin 30 =6*\frac{1}{2}=3
El cateto opuesto al ángulo de 30 grados mide 3 unidades.
Comparando con las opciones del problema, la respuesta correcta es la C.
Reactivo 10: Rango de una función real
Calcula el rango de la función y={e}^{\left(6x-\frac{1}{6}\right)}+6
- \left(6,\infty \right)
- \left(-6,\infty \right)
- [6,\infty )
- [-6,\infty )
Solución:
Calcular el rango de una función real se resume en determinar la inversa de f y, posteriormente, calcular el dominio de {f}^{-1} , el conjunto solución corresponde al rango de f .
Inversa de f\to {f}^{-1}={y}^{-1} , despejamos a x .
y={e}^{\left(6x-\frac{1}{6}\right)}+6\to y-6={e}^{\left(6x-\frac{1}{6}\right)}
Aplicamos logaritmo natural en ambos miembros.
ln \left(y-6\right) =6x-\frac{1}{6}\to ln \left(y-6\right) +\frac{1}{6}=6x
Dividimos por 6.
x={y}^{-1}={f}^{-1}=\frac{1}{6}ln \left(y-6\right) +\frac{1}{36}
Para el dominio de {f}^{-1} , solo tomaremos en cuenta el término con el logaritmo natural, ya que el otro término es una constante. El argumento de toda función logarítmica debe ser mayor que cero:
y-6>0
Despejando nos queda.
y>6
Concluimos entonces que el rengo de la función y={e}^{\left(6x-\frac{1}{6}\right)}+6 son todos los reales mayores a 6.
Ran\left\{y={e}^{\left(6x-\frac{1}{6}\right)}+6\right\}=\forall x\in \left(6,\infty \right)
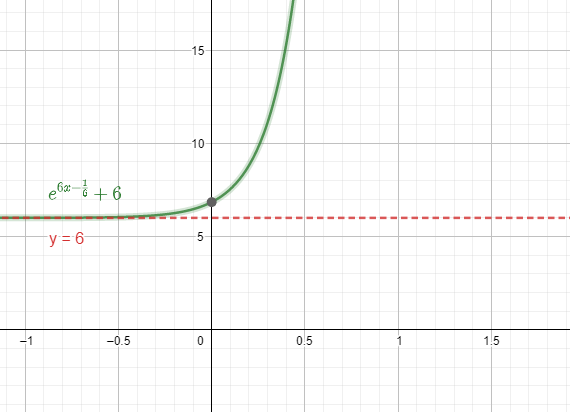
Seleccionamos como respuesta correcta a la opción A.
Reactivo 11: Distancia entre dos puntos
Calcula la distancia del punto A\left(\mathrm{6,1}\right) al punto B\left(\mathrm{1,1}\right) .
- 7
- \sqrt{53}
- 5
- \sqrt{29}
Solución:
La distancia entre dos puntos en el plano real se calcula con la siguiente fórmula:
d\left(A,B\right)=\sqrt{{\left({x}_{a}-{x}_{b}\right)}^{2}+{\left({y}_{a}-{y}_{b}\right)}^{2}}
Donde:
\left({x}_{a},{y}_{a}\right)=\left(\mathrm{6,1}\right)
\left({x}_{b},{y}_{b}\right)=\left(\mathrm{1,1}\right)
Sustituimos.
d\left(A,B\right)=\sqrt{{\left(6-1\right)}^{2}+{\left(1-1\right)}^{2}}
Resolvemos.
d\left(A,B\right)=\sqrt{{\left(6-1\right)}^{2}+{\left(1-1\right)}^{2}}=\sqrt{{5}^{2}+0}=\sqrt{25}
d\left(A,B\right)=5
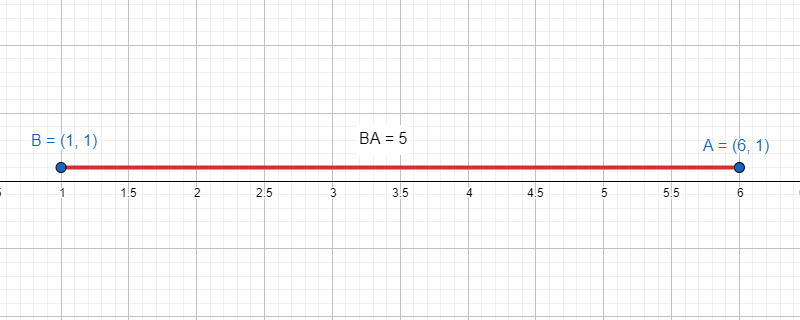
Comparando con las opciones, seleccionamos como respuesta correcta al inciso C.
Reactivo 12: Distancia entre dos puntos
¿Cuál es la distancia entre los puntos P\left(\mathrm{2,5}\right) y Q(4,-1) ?
- 4\sqrt{5}
- 2\sqrt{5}
- 4\sqrt{10}
- 2\sqrt{10}
Solución:
Calculamos la distancia entre P y Q empleando la ecuación:
d\left(P,Q\right)=\sqrt{{\left({x}_{p}-{x}_{q}\right)}^{2}+{\left({y}_{p}-{y}_{q}\right)}^{2}}
Donde:
\left({x}_{p},{y}_{q}\right)=\left(\mathrm{2,5}\right)
\left({x}_{p},{y}_{q}\right)=\left(4,-1\right)
Sustituimos.
d\left(P,Q\right)=\sqrt{{\left(2-4\right)}^{2}+{\left(5+1\right)}^{2}}
Resolvemos.
d\left(P,Q\right)=\sqrt{{\left(-2\right)}^{2}+{6}^{2}}=\sqrt{4+36}=\sqrt{40}=2\sqrt{10}
d\left(P,Q\right)=2\sqrt{10}
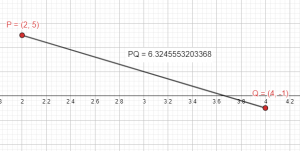
Concluimos seleccionando como correcta la opción D.
Reactivo 13: Punto medio
Encuentra las coordenadas del punto medio entre los puntos P\left(\mathrm{0,2}\right) y Q\left(\mathrm{4,6}\right) .
- \mathrm{2,3}
- \left(\mathrm{2,4}\right)
- \left(\mathrm{3,3}\right)
- \left(\mathrm{3,4}\right)
Solución:
El punto medio M de un segmento con extremos P y Q , es aquel que lo divide en dos partes iguales. Las coordenadas de dicho punto se calculan mediante la siguiente expresión:
{M}_{x}=\frac{{P}_{x}+{Q}_{x}}{2}
{M}_{y}=\frac{{P}_{y}+{Q}_{y}}{2}
Sustituimos las coordenadas de P y Q .
{M}_{x}=\frac{0+4}{2}=2
{M}_{y}=\frac{2+6}{2}=4
Las coordenadas del punto medio entre P\left(\mathrm{0,2}\right) y Q\left(\mathrm{4,6}\right) son \left(\mathrm{2,4}\right) .
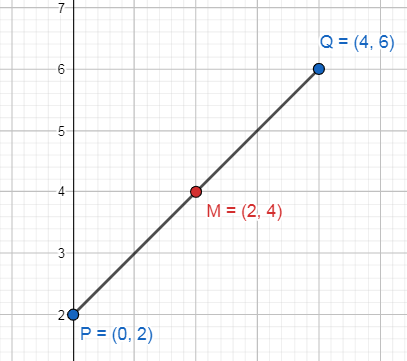
Concluimos el problema seleccionando como correcta a la opción B.
Reactivo 14: Ecuación de la circunferencia
Considerando a la circunferencia como lugar geométrico, ¿Qué expresión algebraica cumple que las coordenadas de los puntos P\left(x,y\right) cuya distancia al origen es 10?
- {x}^{2}-{y}^{2}-100=0
- {x}^{2}-{y}^{2}-10=0
- {x}^{2}+{y}^{2}-100=0
- {x}^{2}+{y}^{2}-10=0
Solución:
La circunferencia es el lugar geométrico cuyos puntos distan igual de otro punto fijo C llamado centro.
{\left(x-{c}_{x}\right)}^{2}+{\left(y-{c}_{y}\right)}^{2}={r}^{2}
En este caso, el centro es el origen de coordenada C\left(\mathrm{0,0}\right) y la distancia fija, denominada radio, es igual a 10 unidades, r=10 . Sustituimos los valores dados por el enunciado.
{\left(x-0\right)}^{2}+{\left(y-0\right)}^{2}={10}^{2}
Simplificamos.
{x}^{2}+{y}^{2}=100
{x}^{2}+{y}^{2}-100=0
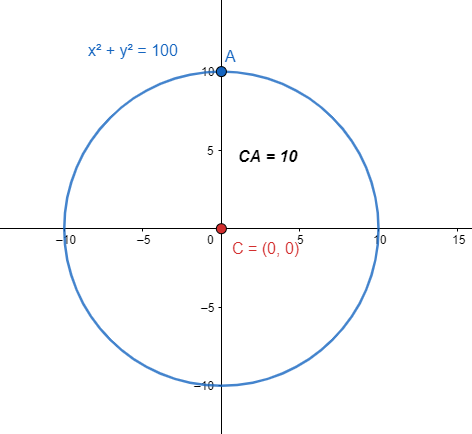
Finalizamos el problema seleccionando como correcta a la opción C.
Sigue practicando con este examen simulacro de 50 ejercicios de matemáticas del examen de la UNAM
Reactivo 15: Ecuación de la parábola
La ecuación de la parábola con vértice V\left(\mathrm{3,4}\right) , parámetro p igual a 5 y eje focal paralelo al eje y es:
- {x}^{2}+6x+20y+89=0
- {y}^{2}-6x+20y+89=0
- {y}^{2}-6x-20y+89=0
- {x}^{2}-6x-20y+89=0
Solución:
Una parábola con eje focal paralelo al eje y , tiene como variable elevada al cuadrado la x . Además, como el signo de p=5 es positivo, sabemos que la parábola abre hacia arriba. La ecuación sería:
{\left(x-h\right)}^{2}=4p\left(y-k\right)
Donde h y k , son las coordenadas del vértice de la parábola, en nuestro caso V\left(\mathrm{3,4}\right) . Procedemos a sustituir los valores dados.
{\left(x-3\right)}^{2}=4\left(5\right)\left(y-4\right)
Desarrollamos.
{x}^{2}-6x+9=20\left(y-4\right)
{x}^{2}-6x+9=20y-80
{x}^{2}-6x-20y+89=0
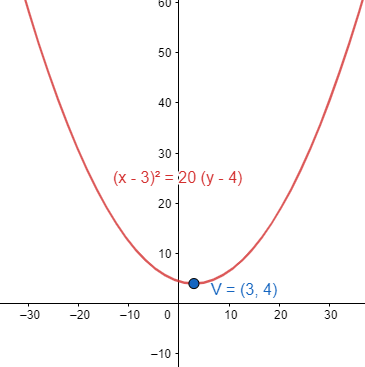
Concluimos seleccionando como respuesta correcta la opción D.
Reactivo 16: Ecuación de la elipse
De las siguientes ecuaciones, ¿Cuál tiene los valores de a , b y c iguales a la elipse
\frac{{x}^{2}}{16}+\frac{{y}^{2}}{4}=1 ?
- 4{x}^{2}+{y}^{2}-16=0
- {x}^{2}+4{y}^{2}+16=0
- {x}^{2}+4{y}^{2}-16=0
- 4{x}^{2}+4{y}^{2}+16=0
Solución:
Para encontrar la respuesta correcta, solo debemos desarrollar la ecuación de la elipse indicada por el enunciado y luego comparar el resultado con los incisos.
El hecho de que la expresión desarrollada y la que se encuentra en el inciso sean iguales es evidencia inequívoca para afirmar que a , b y c son iguales. Comenzamos multiplicando toda la expresión por 16.
\frac{{x}^{2}}{16}+\frac{{y}^{2}}{4}=1\to {x}^{2}+\frac{16{y}^{2}}{4}=16
{x}^{2}+4{y}^{2}=16
{x}^{2}+4{y}^{2}-16=0
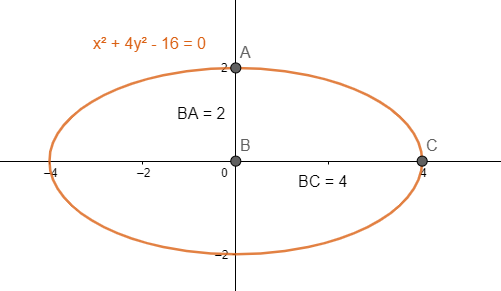
Concluimos al escoger como respuesta correcta la opción C.
Reactivo 17: La hipérbola
Determina las coordenadas de los focos de la hipérbola
\frac{(x-4{)}^{2}}{16}-\frac{(y+1{)}^{2}}{9}=1- F\left(\mathrm{4,2}\right);{F}^{\text{'}}\left(4,-4\right)
- F\left(0,-1\right);{F}^{\text{'}}\left(8,-1\right)
- F\left(-\mathrm{1,1}\right);{F}^{\text{'}}\left(\mathrm{9,1}\right)
- F\left(-1,-1\right);{F}^{\text{'}}\left(9,-1\right)
Solución:
Primero, debemos identificar si la hipérbola tiene el eje focal paralelo a las x o y . Esto se observa identificando la variable positiva, en este caso es la x y, por ende, el eje focal se encuentra paralelo al eje de las x .
Para una hipérbola con centro C=\left(h,k\right)=\left(4,-1\right) y eje focal paralelo a las x , las coordenadas de los focos se obtienen como:
F\left(h-c,k\right);{F}^{\text{'}}\left(h+c,k\right)
Podemos calcular a c con la siguiente ecuación.
c=\sqrt{{a}^{2}+{b}^{2}}=\sqrt{16+9}=5
Sustituimos.
F\left(4-5,-1\right);{F}^{\text{'}}\left(4+5,-1\right)
F\left(-1,-1\right);{F}^{\text{'}}\left(9,-1\right)
Comparando con las opciones del problema, la respuesta correcta está en el inciso D.
Reactivo 18: Discriminante del lugar geométrico
Si en la ecuación A{x}^{2}+Bxy+C{y}^{2}+Dx+Ey+F=0 el discriminante {B}^{2}-4AC es positivo, entonces la ecuación representa una
- Circunferencia
- Parábola
- Elipse
- Hipérbola
Solución:
La ecuación en el enunciado del problema corresponde a la ecuación general de segundo grado y representa la definición analítica de las cónicas.
Uno de los criterios para identificar el tipo de cónica según los coeficientes de la ecuación, se basa en analizar el discriminante.
{B}^{2}-4AC
Si el mismo es mayor que cero (discriminante positivo), entonces la ecuación de la cónica corresponde a una hipérbola. En base a lo anterior, finalizamos escogiendo como respuesta correcta la opción D.
Reactivo 19: Límite de una función
Determina el \underset{x\to a}{lim} \left(f\right(x)-g(x\left)\right) , si tiene que \underset{x\to a}{lim} f\left(x\right)=k y que \underset{x\to a}{lim} g\left(x\right)=-k
- -{k}^{2}
- -2k
- 2k
- {k}^{2}
Solución:
Para resolver este límite, el enunciado no indica directamente cuales son las funciones f y g , pero si proporciona cuánto vale el límite de cada una cuando x\to a . Debemos entonces transformar el límite para que quede en función de los límites de f y g .
Aplicamos la propiedad del límite de una suma.
\underset{x\to a}{lim} \left(f\left(x\right)-g\left(x\right)\right)=\underset{x\to a}{lim} f\left(x\right)-\underset{x\to a}{lim} g\left(x\right)
Ahora, sustituimos el límite en a para cada función.
\underset{x\to a}{lim} f\left(x\right)-\underset{x\to a}{lim} g\left(x\right)=k-\left(-k\right)=k+k=2k
Finalmente.
\underset{x\to a}{lim} \left(f\left(x\right)-g\left(x\right)\right)=2k
Seleccionamos como respuesta correcta la opción C.
Reactivo 20: Derivada de orden superior
Si f\left(x\right)={e}^{\frac{3}{2}+x} determina {f}^{IV}\left(x\right) .
- {f}^{IV}\left(x\right)=4{e}^{\frac{3}{2}+x}
- {f}^{IV}\left(x\right)={e}^{\frac{3}{2}+x}
- {f}^{IV}\left(x\right)=-{e}^{\frac{3}{2}+x}
- {f}^{IV}\left(x\right)=-4{e}^{\frac{3}{2}+x}
Solución:
Para calcular la enésima derivada de una función, derivamos sucesivamente a f , tomando como partida para la siguiente derivada el resultado de la anterior.
Aquí se pueden presentar otros temas relacionados a continuidad y diferenciabilidad, pero como la función del enunciado existe para todos los reales, procedemos sin más.
Primera derivada.
{f}^{\text{'}}\left(x\right)={\left({e}^{\frac{3}{2}+x}\right)}^{\text{'}}
Aplicamos la fórmula para la derivada de una exponencial.
{f}^{\text{'}}\left(x\right)={\left(\frac{3}{2}+x\right)}^{\text{'}}{e}^{\frac{3}{2}+x}=\left(0+1\right){e}^{\frac{3}{2}+x}
{f}^{\text{'}}\left(x\right)={e}^{\frac{3}{2}+x}
Démonos cuenta que, aunque hagamos la segunda, tercera y cuarta derivada, la función resultante seguirá siendo {e}^{\frac{3}{2}+x} . Esto es así, porque el exponente es lineal y al aplicar la fórmula de derivación \frac{3}{2}+x será siempre 1.
Segunda derivada.
{f}^{\text{'}\text{'}}\left(x\right)={\left[{f}^{\text{'}}\left(x\right)\right]}^{\text{'}}={\left(\frac{3}{2}+x\right)}^{\text{'}}{e}^{\frac{3}{2}+x}={e}^{\frac{3}{2}+x}
Tercera derivada.
{f}^{\text{'}\text{'}\text{'}}\left(x\right)={\left[{f}^{\text{'}\text{'}}\left(x\right)\right]}^{\text{'}}={\left(\frac{3}{2}+x\right)}^{\text{'}}{e}^{\frac{3}{2}+x}={e}^{\frac{3}{2}+x}
Cuarta derivada.
{f}^{IV}\left(x\right)={\left[{f}^{\text{'}\text{'}\text{'}}\left(x\right)\right]}^{\text{'}}={\left(\frac{3}{2}+x\right)}^{\text{'}}{e}^{\frac{3}{2}+x}={e}^{\frac{3}{2}+x}
{f}^{IV}\left(x\right)={e}^{\frac{3}{2}+x}
Concluimos indicando como respuesta correcta la opción B.
Reactivo 21: Ecuaciones del movimiento
La posición de una partícula expresada en unidades (u) está dada por la función de tiempo f\left(t\right)={t}^{3}-t+1 . Considerando t=3 , ¿Cuál es su aceleración en \left[\frac{u}{{s}^{2}}\right] ?
- 24\frac{u}{{s}^{2}}
- 26\frac{u}{{s}^{2}}
- 17\frac{u}{{s}^{2}}
- 18\frac{u}{{s}^{2}}
Solución:
A partir de las ecuaciones de la cinemática, sabemos que la aceleración de un cuerpo es igual al cambio respecto del tiempo de la velocidad a=\frac{dv}{dt} y, a su vez, la velocidad representa al cambio de posición respecto del tiempo v=\frac{dx}{dt} .
Si sustituimos a la velocidad en la ecuación de aceleración nos queda.
a=\frac{{d}^{2}x}{d{t}^{2}}
Para calcular la expresión de la aceleración, debemos encontrar la segunda derivada de la posición.
a={\left({t}^{3}-t+1\right)}^{\text{'}\text{'}}={\left(3{t}^{2}-1\right)}^{\text{'}}=6t
Sustituimos ahora t=3 s .
a\left(t=3\right)=6\left(3\right)=18\frac{u}{{s}^{2}}
La aceleración de la partícula en t=3 s es 18\frac{u}{{s}^{2}} .
Comparando con las opciones, seleccionamos como correcta la D.
Reactivo 22: Puntos de inflexión
La abscisa del punto de inflexión de la función f\left(x\right)={x}^{3}-6{x}^{2}+3 es
- 1
- -13
- 2
- -29
Solución:
Para calcular los puntos de inflexión de una función real, debemos emplear el criterio de la segunda derivada:
Si existe cambio de signo, antes y después en una de las raíces de la segunda derivada de f , entonces dicha raíz es un punto de inflexión de f .
Comencemos por calcular la segunda derivada de la función.
{f}^{\text{'}\text{'}}\left(x\right)={\left({x}^{3}-6{x}^{2}+3\right)}^{\text{'}\text{'}}={\left(3{x}^{2}-12x\right)}^{\text{'}}
{f}^{\text{'}\text{'}}\left(x\right)=6x-12
Ahora, igualamos a cero {f}^{\text{'}\text{'}} y calculamos las raíces.
6x-12=0\to x=2
La abscisa x=2 es candidata a punto de inflexión de f . Para comprobar, hacemos un estudio de signos un poco antes y un poco después de {f}^{\text{'}\text{'}} en x=2 . Escogemos a {x}_{izq}=1 y {x}_{der}=3 .
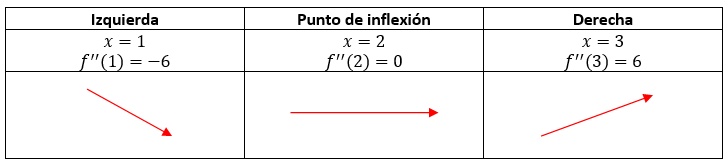
Concluimos indicando a x=2 como punto crítico de f\left(x\right)={x}^{3}-6{x}^{2}+3 .
Comparando con los incisos, escogemos como respuesta correcta al C.
Reactivo 23: Integral indefinida por símbolo del diferencial
La \int cos8xdx es igual a:
- -8x +c
- -8x +c
- \frac{x }{8}+c
- \frac{8x }{8}+c
Solución:
En este caso, la función integrando es un coseno con argumento igual a 8x . Debido a que nuestro diferencial es dx para que corresponda al de 8x debemos multiplicar y dividir la integral por 8.
i=\int \mathrm{cos}8xdx=\frac{1}{8}\int \mathrm{cos}8x8dx
De esta manera, podemos aplicar la fórmula de la integral del coseno.
\int \mathrm{c}\mathrm{o}\mathrm{s}\left(u\right)du=\mathrm{s}\mathrm{i}\mathrm{n}\left(u\right)+c
Resolviendo.
i=\frac{1}{8}\int \mathrm{cos}8x8dx=\frac{1}{8}\mathrm{s}\mathrm{i}\mathrm{n}\left(8x\right)+c
Comparando con las opciones del problema, seleccionamos como respuesta correcta la D.
Reactivo 24: Integral indefinida directa
Obtén la integral de la función \int \frac{dx}{x\mathrm{ln}u}
- \mathrm{xln}ux+c
- \mathrm{uln}ux+c
- \frac{\mathrm{ln}x}{\mathrm{ln}u}+c
- \frac{\mathrm{x}}{\mathrm{ln}\mathrm{u}}+\mathrm{c}
Solución:
La integral parece necesitar un cambio de variables, pero si observas con detenimiento, te darás cuenta que el argumento del logaritmo natural es u y no x , por tanto lnln u es una constante porque no corresponde con nuestra variable de integración x .
\int \frac{dx}{x\mathrm{ln}u}=\frac{1}{\mathrm{ln}u}\int \frac{dx}{x}
Ahora, podemos aplicar la fórmula integral para \frac{1}{x} .
\frac{1}{\mathrm{ln}u}\int \frac{dx}{x}=\frac{1}{\mathrm{ln}u}\mathrm{ln}x+c=\frac{\mathrm{ln}x}{\mathrm{ln}u}+c
Finalmente:
\int \frac{dx}{x\mathrm{ln}u}=\frac{\mathrm{ln}x}{\mathrm{ln}u}+c
Comparando con las opciones, seleccionamos a C como correcta.


