Parte 3 del examen simulacro de matemáticas para carreras de ciencias sociales y administrativas del IPN. Vamos a resolver los ejercicios del 21 al 30 paso a paso.

Es probable que a mitad de camino te puedes sentir agobiado por tanto estudio, no te preocupes, es normal, lo importante es que sigas estudiando, AUNQUE TE EQUIVOQUES.
Reactivo 21
¿Cuál es la pendiente de la recta que forma un ángulo de 30° con la horizontal?
- 5.773
- 0.5773
- 7.73
- 5
Solución:
Por definición, la pendiente de una recta es igual a la tangente del ángulo que forma con la horizontal.
m=\mathrm{tan}\alpha
Sustituimos en la tangente el valor del ángulo:
m=\mathrm{tan}30°=0.5773
La recta que forma un ángulo de 30° con la horizontal, tiene una pendiente de 0.5773.
La respuesta correcta es el inciso b).
Reactivo 22
Relacionar cada parte de la parábola con el elemento representado en la figura.
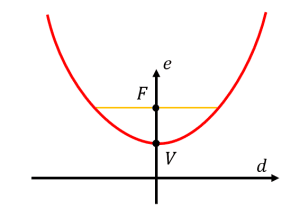

- 1B, 2D, 3A, 4C
- 1B, 2C, 3D, 4A
- 1D, 2C, 3B, 4A
- 1B, 2D, 3C, 4A
Solución:
Para relacionar correctamente los elementos dibujados en la parábola, es necesario conocer de forma previa cómo se construye el lugar geométrico de una parábola. La solución de este problema es netamente teórica.
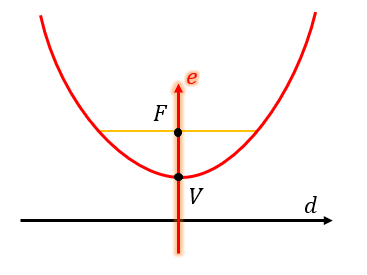
El eje señalado como E , corresponde al eje focal de la parábola, por tanto: 1D.
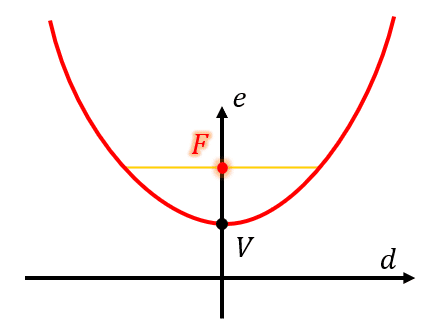
El punto señalado como F , es el foco de la parábola. Indicamos: 2C.
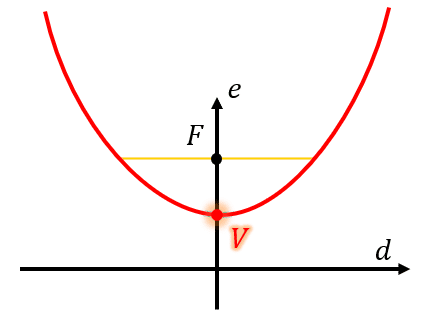
El punto indicado con la letra V , es el vértice de la parábola. 3B. Por descartes, nos queda: 4A. Uniendo todas las respuestas parciales concluimos:
1D, 2C, 3B, 4A.
Finalizamos el ejercicio indicando como respuesta correcta al inciso c).
Reactivo 23
Determine la ecuación de la recta que pasa por el punto \left(1, 1\right) y que es perpendicular a otra recta {l}_{2} , cuya pendiente es m=2 .
- {l}_{2}:y=\frac{3}{2}-\frac{x}{2}
- {l}_{2}:y=\frac{1}{2}-\frac{3x}{2}
- {l}_{2}:y=\frac{3}{2}-\frac{3x}{2}
- {l}_{2}:y=\frac{3}{2}+\frac{x}{2}
Solución:
Para encontrar la ecuación de la recta solicitada, necesitamos dos cosas: su pendiente y un punto que pertenezca a ella. El enunciado nos indica el punto, solo debemos encontrar la pendiente. La siguiente ecuación relaciona las pendientes de dos rectas que son perpendiculares entre sí.
{m}_{2}=-\frac{1}{{m}_{1}}
Sustituimos la pendiente {m}_{1} .
{m}_{2}=-\frac{1}{2}
Finalmente, sustituimos el punto y la pendiente en la ecuación punto-pendiente de la recta.
y-{y}_{o}=m\left(x-{x}_{o}\right)
y-1=-\frac{1}{2}\left(x-1\right)\to y=1-\frac{x}{2}+\frac{1}{2}
y=\frac{3}{2}-\frac{x}{2}
Gráficamente la recta sería:
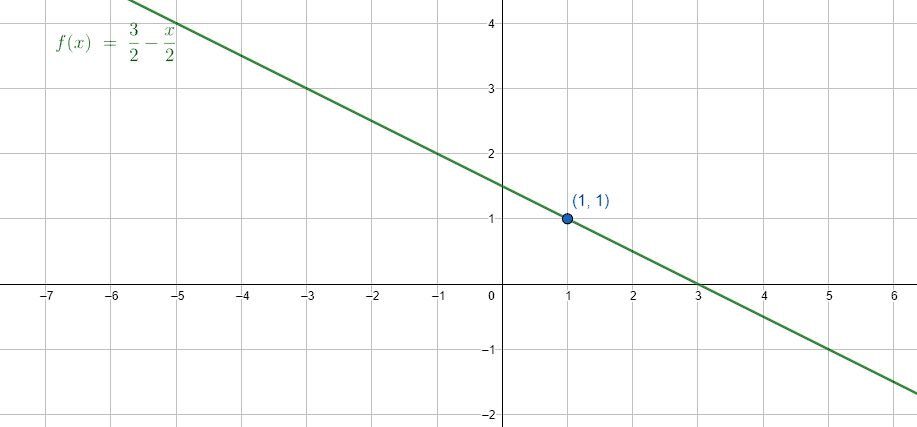
La respuesta correcta es el inciso a).
Reactivo 24
Determine las coordenadas del foco de la parábola y={x}^{2}-x-6 .
- F\left(\frac{1}{2}, 6\right)
- F\left(\frac{1}{2}, -3\right)
- F\left(\frac{1}{2}, -6\right)
- F\left(-6,\frac{1}{2}\right)
Solución:
En el caso de una parábola que abre verticalmente (como la de este caso), las coordenadas del foco se calculan de la siguiente manera:
F\left(h, k\pm p\right)
Donde p es la distancia focal de la parábola, parámetro que se calcula como:
4p=a
Examinando la ecuación de la parábola, sabemos que a=1 .
4p=1\to p=\frac{1}{4}
Ahora debemos calcular las coordenadas del vértice (h, k) . A partir de un desarrollo e igualación de términos obtenemos:
b=-\frac{h}{2p}, c=\frac{{h}^{2}}{4p}+k
Despejamos \left(h, k\right) de las ecuaciones obteniendo:
h=\frac{1}{2}, k=-\frac{25}{4}
Finalmente, el foco tiene como coordenadas:
F\left(\frac{1}{2}, -\frac{25}{4}+\frac{1}{4}\right)=F\left(\frac{1}{2}, -6\right)

La respuesta correcta es el inciso c).
Reactivo 25
¿Cuáles son los cortes con los ejes para la recta 4x+2y-4=0 ?
- a=-1, b=2
- a=1, b=2
- a=1, b=-2
- a=-1, b=-2
Solución:
Podríamos emplear un par de despejes en la ecuación de la recta para calcular los cortes, pero hay una alternativa más rápida y elegante.
Ecuación simétrica de la recta:
\frac{x}{a}+\frac{y}{b}=1
Donde a y b son los cortes con el eje x y y respectivamente. Lo que haremos en este caso es aplicar algunas transformaciones para llegar a esta forma. Iniciamos dividiendo a la ecuación por el mayor coeficiente, es decir: 4.
4x+2y=4\to x+\frac{y}{2}=1
\frac{x}{1}+\frac{y}{2}=1
Finalmente, los cortes con los ejes son:
a=1, b=2
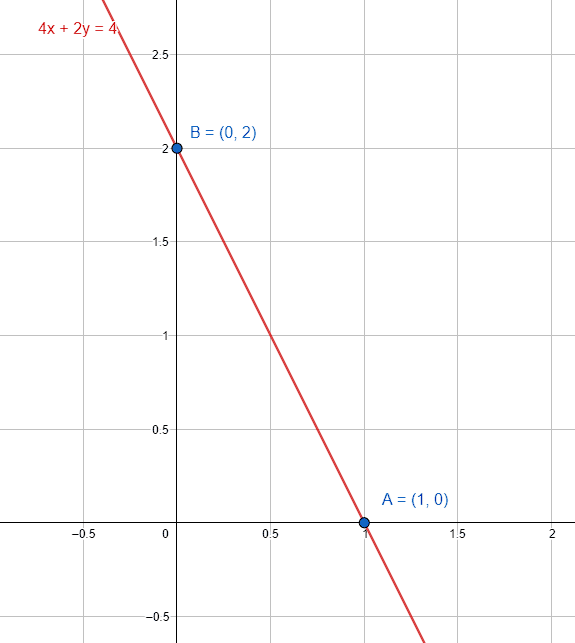
La respuesta correcta es el inciso b).
Reactivo 26
En base a las conclusiones que ofrece el cálculo diferencial, ¿qué significa que el criterio de la segunda derivada de una función en un punto crítico es igual a cero?
- El criterio falla
- La función no es derivable en ese punto
- La función es cóncava
- La función es convexa
Solución:
En cálculo diferencial, el criterio de la segunda deriva es un método que se utiliza para determinar el tipo de concavidad de una función en sus números críticos.
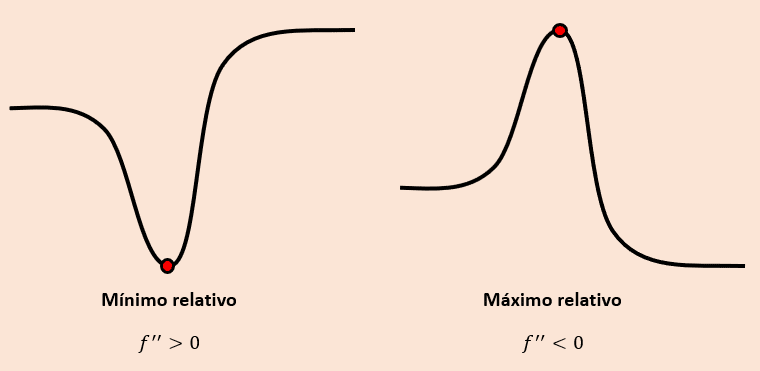
Ahora, cuando la segunda derivada se anula en el punto crítico, se dice que el criterio falla. No es posible llegar a una conclusión acerca de la concavidad o convexidad de la función. La respuesta correcta es el inciso a).
Reactivo 27
Calcule el conjunto solución de la siguiente inecuación.
\frac{4x-1}{5}>2-\frac{x}{2}
- x\in \left(\frac{22}{13}, \infty \right)
- x\in \left(\frac{22}{13}, \infty \right]
- x\in \left[\frac{22}{13}, \infty \right)
- x\in \left(-\frac{22}{13}, \infty \right)
Solución:
Para encontrar el conjunto que describe a la desigualdad, debemos resolverla aplicando las reglas de las desigualdades. Iniciamos agrupando en el primer miembro los términos con x .
\frac{4x-1}{5}>2-\frac{x}{2}\to \frac{4x}{5}-\frac{1}{5}>2-\frac{x}{2}
\frac{4x}{5}-\frac{1}{5}>2-\frac{x}{2}\to \frac{4x}{5}+\frac{x}{2}>2+\frac{1}{5}
Resolvemos la suma de fracciones.
\frac{4x}{5}+\frac{x}{2}>2+\frac{1}{5}\to \frac{8x+5x}{10}>\frac{11}{5}\to \frac{13x}{10}>\frac{11}{5}
Multiplicamos por 10 y dividimos por 13 la expresión.
\frac{13x}{10}>\frac{11}{5}\to x>\frac{110}{65}
x>\frac{22}{13}
El conjunto solución de la inecuación es:
x\in \left(\frac{22}{13}, \infty \right)
La respuesta correcta es el inciso a).
Reactivo 28
Si el \underset{x\to c}{\mathrm{lim}}f\left(x\right)=1 y \underset{x\to c}{\mathrm{lim}}g\left(x\right)=\infty entonces, ¿cuánto vale el \underset{x\to c}{\mathrm{lim}}\frac{f\left(x\right)+1}{g\left(x\right)} ?
- \infty
- 0
- 1
- -1
Solución:
Para resolver este reactivo, empleamos la propiedad del límite de un cociente:
\underset{x\to a}{\mathrm{lim}}\frac{f}{g}=\frac{\underset{x\to a}{\mathrm{lim}}f}{\underset{x\to a}{\mathrm{lim}}g}
Implementado sobre nuestra función nos queda:
\underset{x\to c}{\mathrm{lim}}\frac{f\left(x\right)+1}{g\left(x\right)}=\frac{\underset{x\to c}{\mathrm{lim}}f\left(x\right)+1}{\underset{x\to c}{\mathrm{lim}}g\left(x\right)}
Ahora, aplicamos en el numerador la propiedad del límite de una suma.
\frac{\underset{x\to c}{\mathrm{lim}}f\left(x\right)+1}{\underset{x\to c}{\mathrm{lim}}g\left(x\right)}=\frac{\underset{x\to c}{\mathrm{lim}}f\left(x\right)+\underset{x\to c}{\mathrm{lim}}1}{\underset{x\to c}{\mathrm{lim}}g\left(x\right)}
El enunciado nos dice el valor de cada límite, por tanto, solo nos queda evaluar:
\frac{\underset{x\to c}{\mathrm{lim}}f\left(x\right)+\underset{x\to c}{\mathrm{lim}}1}{\underset{x\to c}{\mathrm{lim}}g\left(x\right)}=\frac{1+1}{\infty }=\frac{2}{\infty }
Cualquier número dividido entre infinito es cero. Finalmente:
\underset{x\to c}{\mathrm{lim}}\frac{f\left(x\right)+1}{g\left(x\right)}=0
La respuesta correcta es el inciso b).
Reactivo 29
Calcula el valor del siguiente límite \underset{x\to 2}{\mathrm{lim}}\mathrm{ln}\left(\frac{x+1}{x-1}\right) .
- 3
- \mathrm{ln}\left(3\right)
- 1
- No existe
Solución:
Iniciamos aplicando la propiedad del límite del logaritmo.
\mathrm{ }\underset{x\to 2}{\mathrm{lim}}\mathrm{ln}\left(\frac{x+1}{x-1}\right)=\mathrm{ }\mathrm{ln}\left(\underset{x\to 2}{\mathrm{lim}}\frac{x+1}{x-1}\right)
Ahora, evaluamos el límite en el punto.
\mathrm{ln}\left(\underset{x\to 2}{\mathrm{lim}}\frac{x+1}{x-1}\right)=\mathrm{ln}\left(\frac{2+1}{2-1}\right)=\mathrm{ln}\left(\frac{3}{1}\right)=\mathrm{ln}\left(3\right)
Finalmente:
\underset{x\to 2}{\mathrm{lim}}\mathrm{ln}\left(\frac{x+1}{x-1}\right)=\mathrm{ln}\left(3\right)
Respuesta correcta: b).
Reactivo 30
Calcular los puntos de inflexión para la siguiente función.
f\left(x\right)={x}^{3}-2{x}^{2}+x+1
- PI\left(\frac{2}{3},\frac{29}{27}\right)
- PI\left(\frac{2}{3},-\frac{29}{27}\right)
- PI\left(-\frac{2}{3},\frac{29}{27}\right)
- PI\left(-\frac{2}{3},-\frac{29}{27}\right)
Solución:
Los puntos de inflexión de una función, son aquellos valores en los que ocurre un cambio de concavidad en la función. Dichos puntos se determinan obteniendo las raíces de la segunda derivada de f\left(x\right) .
Puntos de inflexión:
{f}^{\text{'}\text{'}}\left(x\right)=0
Calculamos primero la segunda derivada.
{f}^{\text{'}\text{'}}\left(x\right)=6x-4
Igualamos a cero y despejamos.
6x-4=0\to x=\frac{2}{3}
La función f\left(x\right) posee un solo punto de inflexión en x=\frac{2}{3} . Evaluamos en f\left(x\right) para obtener la imagen.
f\left(\frac{2}{3}\right)=\frac{29}{27}
PI\left(\frac{2}{3},\frac{29}{27}\right)

La respuesta correcta es el inciso a).


